12 gleich temperamentvoll - 12 equal temperament
Zwölftonkompositionen gleich Temperament ist das Musiksystem , dass teilt die Oktave in 12 Teile, die sich alle gleich temperiert (gleich beabstandeten) auf einer logarithmischen Skala , mit einem Verhältnis gleich dem 12. Wurzel von 2 ( 12 √ 2 ≈ 1,05946). Das resultierende kleinste Intervall, 1 ⁄ 12 der Breite einer Oktave, wird Halbton- oder Halbtonschritt genannt .
Die zwölftönige gleichschwebende Stimmung ist heute das am weitesten verbreitete System in der Musik. Es ist die vorherrschende Stimmungssystem der westlichen Musik gewesen, beginnend mit der klassischen Musik , seit dem 18. Jahrhundert, und Europa fast ausschließlich Annäherungen es seit Jahrtausenden davor verwendet. Es wurde auch in anderen Kulturen verwendet.
In der heutigen Zeit wird 12-TET normalerweise relativ zu einer Standardtonhöhe von 440 Hz gestimmt , die als A440 bezeichnet wird , was bedeutet, dass eine Note, A , auf 440 Hertz gestimmt ist und alle anderen Noten als ein Vielfaches von Halbtönen davon entfernt definiert sind, entweder höher oder niedriger in der Frequenz . Die Standardtonhöhe war nicht immer 440 Hz. Sie hat sich in den letzten hundert Jahren stark verändert und ist im Allgemeinen gestiegen.
Geschichte
Die beiden Figuren, denen häufig die exakte Berechnung der zwölftönigen gleichschwebenden Stimmung zugeschrieben wird, sind Zhu Zaiyu (auch als Chu-Tsaiyu romanisiert. Chinesisch:朱載堉) im Jahr 1584 und Simon Stevin im Jahr 1585. Nach Fritz A. Kuttner, a Kritiker der Theorie ist bekannt, dass "Chu-Tsaiyu 1584 eine hochpräzise, einfache und geniale Methode zur arithmetischen Berechnung gleichschwebender Monochords präsentierte" und dass "Simon Stevin eine mathematische Definition von gleichschwebender Temperatur plus etwas weniger anbot genaue Berechnung der entsprechenden Zahlenwerte im Jahre 1585 oder später." Die Entwicklungen erfolgten unabhängig voneinander.
Kenneth Robinson schreibt Zhu Zaiyu die Erfindung der Temperamentsgleichheit zu und liefert Textzitate als Beweise. Zhu Zaiyu wird mit den Worten zitiert, dass ich in einem Text aus dem Jahr 1584 ein neues System gegründet habe finden Sie die genauen Zahlen für die Pitchpipers in zwölf Operationen." Kuttner widerspricht und bemerkt, dass seine Behauptung "ohne wesentliche Einschränkungen nicht als richtig angesehen werden kann". Kuttner schlägt vor, dass weder Zhu Zaiyu noch Simon Stevin das gleiche Temperament erreichten und keiner von beiden als Erfinder behandelt werden sollte.
China
Frühe Geschichte
Ein vollständiger Satz bronzener Glocken, unter vielen Musikinstrumenten, die im Grab des Marquis Yi von Zeng (frühe kriegerische Staaten, ca. 5. Jahrhundert v. Chr. in der chinesischen Bronzezeit) gefunden wurden, umfasst fünf volle 7-Noten-Oktaven in der Tonart C-Dur mit 12 Halbtönen in der Mitte des Tonumfangs.
Eine Annäherung an das gleiche Temperament wurde von He Chengtian , einem Mathematiker der südlichen und nördlichen Dynastien , der von 370 bis 447 lebte. Er kam mit der frühesten aufgezeichneten ungefähren Zahlenfolge in Bezug auf die gleiche Temperatur in der Geschichte heraus: 900 849 802 758 715 677 638 601 570 536 509,5 479 450.
Zhu Zaiyu
Zhu Zaiyu (朱載堉), ein Fürst des Ming- Hofes, forschte dreißig Jahre lang auf der Grundlage der von seinem Vater ursprünglich postulierten Idee der Gleichheit des Temperaments. Er beschrieb seine neue Tonhöhentheorie in seiner 1580 veröffentlichten Fusion of Music and Calendar . Es folgte die Veröffentlichung einer detaillierten Darstellung der neuen Theorie der gleichschwebenden Temperatur mit einer genauen numerischen Spezifikation für 12-TET in seinen 5.000 -seitiges Werk Complete Compendium of Music and Pitch ( Yuelü quan shu樂律全書) im Jahr 1584. Eine erweiterte Darstellung wird auch von Joseph Needham gegeben. Zhu erhalten sein Ergebnis mathematisch durch die Länge der Kettenteilungs und Rohres nacheinander von 12 √ 2 ≈ 1,059463, und für die Rohrlänge von 24 √ 2 , so dass nach zwölf Unterteilungen (eine Oktave) die Länge um einen Faktor von 2 geteilt wurde:
Ebenso wurde nach 84 Unterteilungen (7 Oktaven) die Länge durch den Faktor 128 geteilt:
Zhu Zaiyu gilt als die erste Person, die das Problem der Gleichheit der Temperamente mathematisch gelöst hat. Mindestens ein Forscher hat vorgeschlagen, dass Matteo Ricci , ein Jesuit in China, diese Arbeit in seinem persönlichen Tagebuch aufgezeichnet und möglicherweise nach Europa zurückgeschickt hat. (Standardressourcen zu diesem Thema erwähnen keinen solchen Transfer.) Im Jahr 1620 wurde Zhus Werk von einem europäischen Mathematiker zitiert. Murray Barbour sagte: "Das erste bekannte gedruckte Erscheinen der korrekten Zahlen für gleiches Temperament war in China, wo die brillante Lösung von Prinz Tsaiyü ein Rätsel bleibt." Das aus dem 19. Jahrhundert deutschen Physiker Hermann von Helmholtz in schrieb An den Tonempfindungen , dass ein chinesischer Prinz (siehe unten) wurde eine Skala von sieben Noten, und dass die Teilung der Oktave in zwölf Halbtonschritte wurde in China entdeckt.
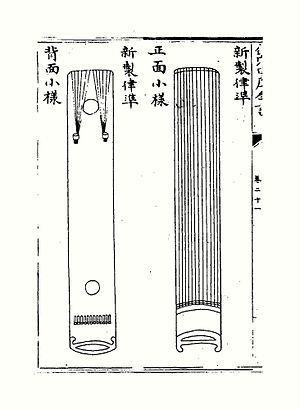
Zhu Zaiyu illustrierte seine Theorie der gleichschwebenden Stimmung durch den Bau eines Satzes von 36 Bambus-Stimmpfeifen in 3 Oktaven, mit Anweisungen zur Bambusart, Farbe der Farbe und detaillierten Angaben zu Länge und Innen- und Außendurchmesser. Er konstruierte auch ein 12-saitiges Stimminstrument mit einem Satz Stimmpfeifen, die in seinem unteren Hohlraum versteckt sind. Im Jahr 1890 duplizierte Victor-Charles Mahillon , Kurator des Conservatoire-Museums in Brüssel, eine Reihe von Stimmpfeifen nach den Vorgaben von Zhu Zaiyu. Er sagte, dass die chinesische Tontheorie mehr über die Länge von Stimmpfeifen wisse als ihr westliches Gegenstück, und dass der Satz von Pfeifen, der gemäß den Zaiyu-Daten dupliziert wurde, die Richtigkeit dieser Theorie bewies.
Europa
Frühe Geschichte
Eine der frühesten Diskussionen über gleiches Temperament findet sich in den Schriften von Aristoxenus im 4. Jahrhundert v.
Vincenzo Galilei (Vater von Galileo Galilei ) war einer der ersten praktischen Verfechter der Zwölftongleichheit. Er komponierte eine Reihe von Tanzsuiten zu jedem der 12 Töne der chromatischen Tonleiter in allen "Transpositionstonarten" und veröffentlichte in seinem 1584 erschienenen " Fronimo " auch 24 + 1 ricercars . Er verwendete das 18:17-Verhältnis für die Bundierung der Laute (obwohl für reine Oktaven einige Anpassungen erforderlich waren).
Galileis Landsmann und Lautenistenkollege Giacomo Gorzanis hatte 1567 Musik geschrieben, die auf gleichschwebendem Temperament beruhte. Gorzanis war nicht der einzige Lautenist, der alle Tonarten oder Tonarten erforschte: Francesco Spinacino schrieb bereits ein "Recercare de tutti li Toni" ( Ricercar in allen Tönen). als 1507. Im 17. Jahrhundert schrieb der Lautenist und Komponist John Wilson einen Satz von 30 Präludien, davon 24 in allen Dur/Moll-Tonarten. Eine enge Annäherung an die gleichschwebende Stimmung zog Henricus Grammateus 1518. Die ersten gleichschwebenden Stimmregeln wurden von Giovani Maria Lanfranco in seiner "Scintille de musica" gegeben. Zarlino wandte sich in seiner Polemik mit Galilei zunächst gegen die gleichschwebende Stimmung, räumte sie jedoch 1588 in Bezug auf die Laute in seinen Sopplimenti musicali ein.
Simon Steven
Die erste Erwähnung von gleichschwebendem Temperament im Zusammenhang mit der zwölften Wurzel von zwei im Westen erschien in Simon Stevins Manuskript Van De Spiegheling der singconst (ca. 1605), das fast drei Jahrhunderte später im Jahr 1884 posthum veröffentlicht wurde Nach seiner Berechnung lagen viele der erhaltenen Akkordlängenzahlen um ein oder zwei Einheiten von den richtigen Werten ab. Als Ergebnis haben die Frequenzverhältnisse der Akkorde von Simon Stevin kein einheitliches Verhältnis, sondern ein Verhältnis pro Ton, was von Gene Cho als falsch behauptet wird.
Die folgenden Akkordlängen von Simon Stevin aus Van de Spiegheling der singconst :
| Ton | Akkord 10000 von Simon Stevin | Verhältnis | Korrigierter Akkord |
|---|---|---|---|
| Halbton | 9438 | 1.0595465 | 9438.7 |
| ganzer Ton | 8909 | 1.0593781 | |
| Ton und eine Hälfte | 8404 | 1.0600904 | 8409 |
| diton | 7936 | 1.0594758 | 7937 |
| ditone und eine halbe | 7491 | 1.0594046 | 7491.5 |
| triton | 7071 | 1.0593975 | 7071.1 |
| Tritonus und eine Hälfte | 6674 | 1.0594845 | 6674.2 |
| vierfarbig | 6298 | 1.0597014 | 6299 |
| viertönig und ein halbes | 5944 | 1.0595558 | 5946 |
| Fünf-Ton | 5611 | 1.0593477 | 5612.3 |
| fünftönig und ein halbes | 5296 | 1.0594788 | 5297.2 |
| voller Ton | 1.0592000 |
Eine Generation später präsentierte der französische Mathematiker Marin Mersenne mehrere gleich temperierte Akkordlängen, die Jean Beaugrand, Ismael Bouillaud und Jean Galle erhalten hatten.
1630 veröffentlichte Johann Faulhaber eine 100-Cent-Monochord-Tabelle, die aufgrund seiner Verwendung von logarithmischen Tabellen mehrere Fehler enthielt. Er erklärte nicht, wie er zu seinen Ergebnissen kam.
Barockzeit
Von 1450 bis etwa 1800, Zupfinstrument Spieler (lutenists und Gitarristen) in der Regel begünstigt gleich Temperament und die Brossard Laute Manuskript im letzten Viertel des 17. Jahrhunderts zusammengestellt enthält eine Reihe von 18 Präludien zugeschrieben Bocquet in allen Tonarten geschrieben, einschließlich der letzten prelude mit dem Titel Prelude sur tous les tons , das enharmonisch durch alle Tonarten moduliert. Angelo Michele Bartolotti veröffentlichte eine Reihe von Passacaglias in allen Tonarten mit verbindenden enharmonisch modulierenden Passagen. Unter den Klavierkomponisten des 17. Jahrhunderts vertrat Girolamo Frescobaldi die gleichschwebende Stimmung. Einige Theoretiker, wie Giuseppe Tartini , waren gegen die Annahme der gleichen Temperaments; sie waren der Meinung, dass die Herabsetzung der Reinheit jedes Akkords die ästhetische Anziehungskraft der Musik herabsetzte, obwohl Andreas Werckmeister in seiner posthum veröffentlichten Abhandlung von 1707 nachdrücklich für die gleiche Temperierung eintrat.
Die zwölftönige gleichschwebende Stimmung setzte sich aus verschiedenen Gründen durch. Es passte bequem in das vorhandene Tastaturdesign und erlaubte völlige harmonische Freiheit mit der Last mäßiger Unreinheiten in jedem Intervall, insbesondere unvollkommenen Konsonanzen. Dies ermöglichte einen größeren Ausdruck durch enharmonische Modulation , die im 18. Jahrhundert in der Musik von Komponisten wie Francesco Geminiani , Wilhelm Friedemann Bach , Carl Philipp Emmanuel Bach und Johann Gottfried Müthel äußerst wichtig wurde . Die zwölftönige gleichschwebende Stimmung hatte zwar einige Nachteile, wie zum Beispiel unvollkommene Terzen, aber als Europa zur gleichschwebenden Stimmung wechselte, änderte es die Musik, die es schrieb, um sich an das System anzupassen und Dissonanzen zu minimieren.
Die Entwicklung der Temperamentgleichheit ab der Mitte des 18. Frühromantik (erste Dekade des 19. Jahrhunderts), mit Ausnahme der Orgeln, die allmählich darauf umstellten und erst in der zweiten Dekade des 19. Jahrhunderts fertiggestellt wurden. (In England hielten sich einige Domorganisten und Chorleiter auch nach diesem Datum dagegen; Samuel Sebastian Wesley zum Beispiel war die ganze Zeit dagegen. Er starb 1876.)
Eine präzise gleichtemperierte Stimmung ist mit der Sabbatini-Methode aus dem 17. Dies wurde auch von mehreren Schriftstellern während der Klassik vorgeschlagen. Schon in den ersten Jahrzehnten des 19. Die Verwendung von Beat Rates, die erstmals 1749 vorgeschlagen wurde, wurde nach ihrer Verbreitung durch Helmholtz und Ellis in der zweiten Hälfte des 19. Jahrhunderts üblich. Die ultimative Präzision war mit 2-Dezimal-Tabellen verfügbar, die 1917 von White veröffentlicht wurden.
In der Umgebung gleichschwebender Temperamente entwickelten und blühten die neuen Stile der symmetrischen Tonalität und Polytonalität , der atonalen Musik, wie sie in der Zwölftontechnik oder des Serialismus geschrieben wurde , und des Jazz (zumindest seine Klavierkomponente).
Vergleich historischer Näherungen des Halbtons
| Jahr | Name | Verhältnis | Cent |
|---|---|---|---|
| 400 | Er Chengtian | 1.060070671 | 101,0 |
| 1580 | Vincenzo Galilei | 18:17 [1.058823529] | 99,0 |
| 1581 | Zhu Zaiyu | 1.059463094 | 100,0 |
| 1585 | Simon Steven | 1.059546514 | 100,1 |
| 1630 | Marin Mersenne | 1.059322034 | 99,8 |
| 1630 | Johann Faulhaber | 1.059490385 | 100,0 |
Mathematische Eigenschaften
Bei der gleichtemperierten Zwölftonstimmung, die die Oktave in 12 gleiche Teile teilt, ist die Breite eines Halbtons , also das Frequenzverhältnis des Intervalls zwischen zwei benachbarten Tönen, die Zwölftelwurzel von zwei :
Dies ist äquivalent zu:
Dieses Intervall ist in 100 Cent unterteilt .
Berechnung absoluter Häufigkeiten
Um die Frequenz P n einer Note in 12-TET zu finden, kann die folgende Definition verwendet werden:
In dieser Formel bezieht sich P n auf die Tonhöhe oder Frequenz (normalerweise in Hertz ), die Sie versuchen zu finden. P a bezieht sich auf die Frequenz einer Referenztonhöhe. n und a beziehen sich auf Zahlen, die der gewünschten Tonhöhe bzw. der Referenztonhöhe zugeordnet sind. Diese beiden Zahlen stammen aus einer Liste von aufeinanderfolgenden ganzen Zahlen, die aufeinanderfolgenden Halbtönen zugeordnet sind. Zum Beispiel ist A 4 (die Referenztonhöhe) die 49. Taste vom linken Ende eines Klaviers (auf 440 Hz gestimmt ), und C 4 ( mittleres C ) und F# 4 sind die 40. bzw. 46. Taste. Diese Zahlen können verwendet werden, um die Häufigkeit von C 4 und F# 4 zu finden :
Nur Intervalle
Die Intervalle von 12-TET kommen einigen Intervallen in reiner Intonation sehr nahe .
Nach Grenze
12-TET ist im 3-Limit sehr genau, aber wenn man die Prime-Limits auf 11 erhöht, wird es jedes Mal um etwa ein Sechstel eines Halbtons allmählich schlechter. Seine elfte und dreizehnte Harmonische sind extrem ungenau. Die siebzehnte und neunzehnte Harmonische von 12-TET sind fast so genau wie die dritte Harmonische, aber zu diesem Zeitpunkt ist die Hauptgrenze zu hoch geworden, um für die meisten Leute konsonant zu klingen.
3-Limit
12-TET hat eine sehr gute Annäherung an die perfekte Quinte (3/2) und ihre Umkehrung , die perfekte Quarte (4/3), insbesondere für die Unterteilung der Oktave in eine relativ kleine Anzahl von Tönen. Genauer gesagt ist eine gerade perfekte Quinte etwas weniger als zwei Cent, was einem Fünfzigstel eines Halbtons entspricht, schärfer als die gleich temperierte Näherung. Da der Durton (9/8) einfach aus zwei perfekten Quinten minus einer Oktave besteht und seine Umkehrung, die pythagoreische kleine Septime (16/9), einfach aus zwei perfekten Quarten zusammen besteht, behalten sie größtenteils die Genauigkeit von ihre Vorgänger; der Fehler wird verdoppelt, aber er bleibt klein – so klein, dass der Mensch ihn nicht wahrnehmen kann. Man kann weiterhin Brüche mit höheren Dreierpotenzen verwenden, die nächsten beiden sind 27/16 und 32/27, aber wenn die Terme der Brüche größer werden, werden sie für das Ohr weniger angenehm.
5-Limit
Die Annäherung von 12-TET an die fünfte Harmonische (5/4) liegt zwischen einem Sechstel und einem Siebtel eines Halbtons. Da Intervalle, die weniger als ein Viertel einer Tonleiter entfernt sind, immer noch gestimmt klingen, hat 12-TET eine gestimmte fünfte Harmonische, die verwendet werden kann, um andere Fünf-Grenzen-Intervalle wie 5/3 und 8/5 zu erzeugen. mit ähnlich großen Fehlern. Westliche Musik macht sich die gestimmte fünfte Harmonische zunutze, indem sie sie beispielsweise in der 4:5:6-Rechenfolge verwendet .
7-Limit
Die Annäherung von 12-TET an die siebte Harmonische (7/4) ist etwa ein Drittel eines Halbtons daneben. Da der Fehler größer als ein Viertel eines Halbtons ist, neigen Intervalle mit sieben Grenzen in 12-TET dazu, verstimmt zu klingen. Bei den Tritonusfraktionen 7/5 und 10/7 heben sich die Fehler der fünften und siebten Harmonischen teilweise auf, so dass die gerechten Brüche innerhalb eines Viertelhalbtons ihrer gleichtemperierten Äquivalente liegen, der Tritonus aber dennoch dissonant klingt zu den meisten Menschen.
11- und 13-Grenzen
Die elfte Harmonische (11/8) beträgt etwa 550 Cent, was bedeutet, dass sie in 12-TET fast genau zwischen den nächsten beiden gleich temperierten Intervallen liegt und daher von beiden nicht angenähert wird. Tatsächlich ist 11/8 in 12-TET fast so weit wie möglich von jeder gleichtemperierten Näherung entfernt. Die dreizehnte Harmonische (13/8) ist fast genauso schlimm. Dies bedeutet jedoch, dass der Bruch 13/11 (und auch seine Umkehrung 22/13) durch 12-TET (insbesondere durch drei Halbtöne) genau angenähert wird, da sich die Fehler der elften und dreizehnten Harmonischen gegenseitig aufheben. Die meisten Menschen sind jedoch nicht an die elfte und dreizehnte Harmonische gewöhnt, daher würde dieser Bruch für die meisten Menschen nicht übereinstimmend klingen. In ähnlicher Weise könnte der Fehler der elften oder dreizehnten Harmonischen größtenteils durch den Fehler der siebten Harmonischen ausgeglichen werden, aber aus dem gleichen Grund wie zuvor würden die meisten Leute die resultierenden Brüche nicht als konsonant finden.
17- und 19-Grenzen
Die siebzehnte Harmonische (17/16) ist nur etwa 5 Cent schärfer als ein Halbton in 12-TET. Sie kann mit der 12-TET-Näherung der dritten Harmonischen kombiniert werden, um 17/12 zu erhalten, die als nächste Pell-Näherung nach 7/5 nur etwa drei Cent vom gleichtemperierten Tritonus (der Quadratwurzel aus zwei) und 17/9, was nur einen Cent von der großen Septime von 12-TET entfernt ist. Die neunzehnte Harmonische ist nur etwa zweieinhalb Cent flacher als drei der 12-TET-Halbtöne, daher kann sie ebenfalls mit der dritten Harmonischen kombiniert werden, um 19/12 zu erhalten, die etwa viereinhalb Cent flacher ist als eine gleichtemperierte kleine Sexte und 19/18, was etwa sechseinhalb Cent flacher ist als ein Halbton. Da 17 und 19 jedoch für Konsonantenverhältnisse ziemlich groß sind und die meisten Menschen mit 17-Grenzen- und 19-Grenzen-Intervallen nicht vertraut sind, sind 17-Grenzen- und 19-Grenzen-Intervalle für die meisten Zwecke nicht nützlich, sodass sie wahrscheinlich nicht als eine Rolle in allen Konsonanzen von 12-TET spielen.
Tisch
In der folgenden Tabelle werden die Größen verschiedener gerechter Intervalle mit ihren gleichmütigen Gegenstücken verglichen, sowohl als Verhältnis als auch in Cent angegeben . Unterschiede von weniger als sechs Cent können von den meisten Menschen nicht wahrgenommen werden, und Intervalle von mehr als einem Viertelschritt, das sind in diesem Fall 25 Cent, klingen verstimmt.
| Anzahl der Schritte | Hinweis von C . nach oben | Genauer Wert in 12-TET | Dezimalwert in 12-TET | Gleichmäßig temperiertes Audio | Cent | Nur Intonationsintervallname | Nur Intonationsintervallbruch | Tongerechter Ton | Cent in nur Intonation | Unterschied |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | C | 2 0 ⁄ 12 = 1 | 1 |
|
0 | Einklang | 1 ⁄ 1 = 1 |
|
0 | 0 |
| 1 | C ♯ oder D ♭ | 2 1 ⁄ 12 = 12 √ 2 | 1.05946… |
|
100 | Septimaler dritter Ton | 28 ⁄ 27 = 1.03703… |
|
62,96 | -37.04 |
| Nur chromatischer Halbton | 25 ⁄ 24 = 1,04166… |
|
70,67 | -29.33 | ||||||
| Undezimaler Halbton | 22 ⁄ 21 = 1.04761… |
|
80,54 | -19.46 | ||||||
| Sepimaler chromatischer Halbton | 21 ⁄ 20 = 1,04 |
|
84.47 | -15,53 | ||||||
| Novendezimaler chromatischer Halbton | 20 ⁄ 19 = 1,05263… |
|
88,80 | -11.20 | ||||||
| Pythagoräischer diatonischer Halbton | 256 ⁄ 243 = 1,05349… |
|
90,22 | -9,78 | ||||||
| Größerer chromatischer Halbton | 135 ⁄ 128 = 1,05468… |
|
92,18 | -7,82 | ||||||
| Novendezimaler diatonischer Halbton | 19 ⁄ 18 = 1,05555… |
|
93,60 | -6,40 | ||||||
| Septadezimaler chromatischer Halbton | 18 ⁄ 17 = 1,05882… |
|
98,95 | -1,05 | ||||||
| Siebzehnte Harmonische | 17 ⁄ 16 = 1,0625… |
|
104,96 | +4,96 | ||||||
| Nur diatonischer Halbton | 16 ⁄ 15 = 1,06666… |
|
111,73 | +11.73 | ||||||
| Pythagoräischer chromatischer Halbton | 2187 ⁄ 2048 = 1,06787… |
|
113,69 | +13,69 | ||||||
| Septimaler diatonischer Halbton | 15 ⁄ 14 = 1,07142… |
|
119.44 | +19.44 | ||||||
| Kleiner tridezimaler 2/3-Ton | 14 ⁄ 13 = 1,07692… |
|
128.30 | +28.30 | ||||||
| Dur diatonischer Halbton | 27 ⁄ 25 = 1,08 |
|
133,24 | +33.24 | ||||||
| 2 | D | 2 2 ⁄ 12 = 6 √ 2 | 1.12246… |
|
200 | Pythagoräisches vermindertes Drittel | 65536 ⁄ 59049 = 1,10985… |
|
180.45 | -19.55 |
| Mollton | 10 ⁄ 9 = 1,11111… |
|
182.40 | -17,60 | ||||||
| Durton | 9 ⁄ 8 = 1,125 |
|
203,91 | +3,91 | ||||||
| Septimaler Ganzton | 8 ⁄ 7 = 1,14285… |
|
231.17 | +31.17 | ||||||
| 3 | D ♯ oder E ♭ | 2 3 / 12 = 4 √ 2 | 1.18920… |
|
300 | Septimale kleine Terz | 7 ⁄ 6 = 1,16666… |
|
266.87 | -33.13 |
| Tridezimale kleine Terz | 13 ⁄ 11 = 1,18181… |
|
289.21 | -10.79 | ||||||
| Pythagoräische kleine Terz | 32 ⁄ 27 = 1,18518… |
|
294.13 | -5,87 | ||||||
| Neunzehnte Harmonische | 19 / 16 = 1,1875 |
|
297.51 | -2,49 | ||||||
| Nur kleine Terz | 6 ⁄ 5 = 1,2 |
|
315,64 | +15,64 | ||||||
| Pythagoräische vergrößerte Sekunde | 19683 ⁄ 16384 = 1,20135… |
|
317,60 | +17,60 | ||||||
| 4 | E | 2 4 / 12 = 3 √ 2 | 1.25992… |
|
400 | Pythagoräische verminderte vierte | 8192 ⁄ 6561 = 1,24859… |
|
384.36 | -15,64 |
| Nur große Drittel | 5 ⁄ 4 = 1,25 |
|
386.31 | -13,69 | ||||||
| Pythagoräische große Terz | 81 ⁄ 64 = 1,265625 |
|
407,82 | +7,82 | ||||||
| Undezimale große Terz | 14 ⁄ 11 = 1,27272… |
|
417,51 | +17,51 | ||||||
| Septimale große Terz | 9 ⁄ 7 = 1,28571… |
|
435.08 | +35.08 | ||||||
| 5 | F | 2 5 / 12 = 12 √ 32 | 1.33484… |
|
500 | Einfach perfekter Vierter | 4 ⁄ 3 = 1,33333… |
|
498.04 | -1,96 |
| Pythagoräisches überhöhtes Drittel | 177147 ⁄ 131072 = 1,35152… |
|
521.51 | -21.51 | ||||||
| 6 | F ♯ oder G ♭ | 2 6 ⁄ 12 = √ 2 | 1.41421… |
|
600 | Klassischer erweiterter Quart | 25 ⁄ 18 = 1,38888… |
|
568,72 | -31.28 |
| Huygens' Tritonus | 7 ⁄ 5 = 1,4 |
|
582.51 | -17.49 | ||||||
| Pythagoräische verminderte Quinte | 1024 ⁄ 729 = 1,40466… |
|
588,27 | -11.73 | ||||||
| Gerade auf vierter erhöht | 45 / 32 = 1,40625 |
|
590.22 | -9,78 | ||||||
| Nur vermindertes Fünftel | 64 ⁄ 45 = 1,42222… |
|
609.78 | +9.78 | ||||||
| Pythagoräische überhöhte Quarte | 729 ⁄ 512 = 1,42382… |
|
611.73 | +11.73 | ||||||
| Eulers Tritonus | 10 ⁄ 7 = 1,42857… |
|
617,49 | +17.49 | ||||||
| Klassische verminderte Quinte | Über 36 / 25 = 1,44 |
|
631,28 | +31.28 | ||||||
| 7 | g | 2 7 / 12 = 12 √ 128 | 1.49830… |
|
700 | Pythagoräisch verminderte sechste | 262144 ⁄ 177147 = 1,47981… |
|
678,49 | -21.51 |
| Einfach perfekter Fünfter | 3 ⁄ 2 = 1,5 |
|
701.96 | +1,96 | ||||||
| 8 | G ♯ oder A ♭ | 2 8 / 12 = 3 √ 4 | 1.58740… |
|
800 | Septimale kleine Sexte | 14 ⁄ 9 = 1,55555… |
|
764,92 | -35.08 |
| Undezimale kleine Sexte | 11 ⁄ 7 = 1,57142… |
|
782.49 | -17.51 | ||||||
| Pythagoräische kleine Sexte | 128 ⁄ 81 = 1,58024… |
|
792.18 | -7,82 | ||||||
| Nur kleine Sexte | 8 ⁄ 5 = 1,6 |
|
813,69 | +13,69 | ||||||
| Pythagoräische überhöhte Quinte | 6561 ⁄ 4096 = 1,60180… |
|
815,64 | +15,64 | ||||||
| 9 | EIN | 2 9 ⁄ 12 = 4 √ 8 | 1.68179… |
|
900 | Pythagoräisch vermindertes Siebtel | 32768 ⁄ 19683 = 1,66478… |
|
882,40 | -18.60 |
| Nur große sechste | 5 ⁄ 3 = 1.66666… |
|
884.36 | -15,64 | ||||||
| Neunzehnte Subharmonische | 32 ⁄ 19 = 1,68421… |
|
902.49 | +2,49 | ||||||
| Pythagoräische große Sexte | 27 / 16 = 1,6875 |
|
905.87 | +5,87 | ||||||
| Septimale große Sexte | 12 ⁄ 7 = 1,71428… |
|
933.13 | +33.13 | ||||||
| 10 | A ♯ oder B ♭ | 2 10 ⁄ 12 = 6 √ 32 | 1.78179… |
|
1000 | Harmonische Siebte | 7 ⁄ 4 = 1,75 |
|
968.83 | -31.17 |
| Pythagoräische kleine Septime | 16 ⁄ 9 = 1,77777… |
|
996.09 | -3,91 | ||||||
| Große kleine Septime | 9 ⁄ 5 = 1,8 |
|
1017,60 | +17,60 | ||||||
| Pythagoräische überhöhte sechste | 59049 ⁄ 32768 = 1,80203… |
|
1019.55 | +19,55 | ||||||
| 11 | B | 2 11 ⁄ 12 = 12 √ 2048 | 1.88774… |
|
1100 | Tridezimal neutral siebte | 13 ⁄ 7 = 1,85714… |
|
1071.70 | -28.30 |
| Pythagoräische verminderte Oktave | 4096 ⁄ 2187 = 1,87288… |
|
1086.31 | -13,69 | ||||||
| Nur große Siebte | 15 ⁄ 8 = 1,875 |
|
1088,27 | -11.73 | ||||||
| 17. Subharmonische | 32 ⁄ 17 = 1,88235… |
|
1095.04 | -4,96 | ||||||
| Pythagoräische große Septime | 243 ⁄ 128 = 1,89843… |
|
1109.78 | +9.78 | ||||||
| Septimale große Septime | 27 ⁄ 14 = 1,92857… |
|
1137.04 | +37.04 | ||||||
| 12 | C | 2 12 ⁄ 12 = 2 | 2 |
|
1200 | Oktave | 2 ⁄ 1 = 2 |
|
1200,00 | 0 |
Kommas
12-TET mildert mehrere Kommas aus , was bedeutet, dass es mehrere Brüche in der Nähe von 1 ⁄ 1 gibt, die von 12-TET aufgrund der Abbildung verschiedener Brüche auf dasselbe gleich temperierte Intervall als 1 ⁄ 1 behandelt werden. Beispielsweise 729 / 512 ( 3 6 / 2 9 ) und 1024 / 729 ( 2 10 / 3 6 ) jeweils an der Tritone kartiert, so dass sie als das gleiche Intervall behandelt werden; daher wird ihr Quotient 531441 ⁄ 524288 ( 3 12 ⁄ 2 19 ) auf unisono abgebildet/behandelt. Dies ist das pythagoräische Komma und es ist das einzige 3-Grenzkomma von 12-TET. Wenn man jedoch die Primzahlgrenze erhöht und mehr Intervalle enthält, erhöht sich die Anzahl der Kommas. 12-TET wichtigsten fünf-limit Komma ist 81 / 80 ( 3 4 / 2 4 × 5 1 ), die als bekannt ist syntonic comma und der Faktor zwischen pythagoreischen Drittel und Sechstel und ihre gerade Pendants. Zu den anderen 5-Grenzkommas von 12-TET gehören:
- Schisma : 32805 ⁄ 32768 = 3 8 × 5 1 ⁄ 2 15 =( 531441 ⁄ 524288 ) 1 ×( 81 ⁄ 80 ) −1
- Diaschisma : 2048 ⁄ 2025 = 2 11 ⁄ 3 4 × 5 2 =( 531441 ⁄ 524288 ) −1 ×( 81 ⁄ 80 ) 2
- Geringere Diesis : 128 ⁄ 125 = 2 7 ⁄ 5 3 =( 531441 ⁄ 524288 ) −1 ×( 81 ⁄ 80 ) 3
- Größer diesis : 648 / 625 = 2 3 × 3 - 4 / 5 4 = ( 531441 / 524288 ) -1 × ( 81 / 80 ) 4
Eines der 7-limit Kommata , dass 12-TET mildert out ist die septimal Kleisma , die gleich ist 225 / 224 oder 3 2 × 5 2 / 2 5 × 7 - 1 . Zu den anderen 7-Grenzkommas von 12-TET gehören:
- Semikomma : 126 ⁄ 125 = 2 1 × 3 2 × 7 1 ⁄ 5 3 = ( 81 ⁄ 80 ) 1 × ( 225 ⁄ 224 ) −1
- Komma von Archytas : 64 ⁄ 63 = 2 6 ⁄ 3 2 ×7 1 =( 531441 ⁄ 524288 ) −1 ×( 81 ⁄ 80 ) 2 ×( 225 ⁄ 224 ) 1
- Septimaler Viertelton : 36 ⁄ 35 = 2 2 × 3 2 ⁄ 5 1 × 7 1 =( 531441 ⁄ 524288 ) −1 × ( 81 ⁄ 80 ) 3 × ( 225 ⁄ 224 ) 1
- Jubilisma : 50 ⁄ 49 = 2 1 × 5 2 ⁄ 7 2 =( 531441 ⁄ 524288 ) −1 ×( 81 ⁄ 80 ) 2 ×( 225 ⁄ 224 ) 2
Ähnliche Tuning-Systeme
In der Vergangenheit wurden mehrere Stimmungssysteme verwendet, die als leichte Variationen von 12-TEDO mit zwölf Noten pro Oktave, aber mit einigen Variationen zwischen den Intervallgrößen gesehen werden können, so dass die Noten nicht ganz gleichmäßig verteilt sind. Ein Beispiel dafür ist eine Drei-Grenzen-Skala, bei der gleich temperierte perfekte Quinten von 700 Cent durch gerecht intonierte perfekte Quinten von 701,955 Cent ersetzt werden. Da sich die beiden Intervalle um weniger als 2 Cent oder 1 ⁄ 600 einer Oktave unterscheiden, sind die beiden Tonleitern sehr ähnlich. Tatsächlich entwickelten die Chinesen mindestens ein Jahrhundert bevor He Chengtian die 12-TEDO-Sequenz erschuf , eine 3-Grenze-Intonation . Ebenso Tuning Pythagoreische, die von den alten Griechen entwickelt wurde, war das vorherrschende System in Europa , bis in der Renaissance, als die Europäer erkannt , dass dissonante Intervalle wie 81 / 64 könnte wie auf einfachere Verhältnisse durch Tempern sie mehr Konsonanten gemacht werden 5 / 4 , was dazu führte, dass Europa eine Reihe mitteltöniger Temperamente entwickelte , die die Intervallgrößen leicht veränderten, aber immer noch als ungefähr 12-TEDO angesehen werden konnten. Aufgrund der Tendenz der mitteltonigen Temperamente, den Fehler auf eine enharmonische perfekte Quinte zu konzentrieren, was ihn sehr dissonant macht , haben europäische Musiktheoretiker wie Andreas Werckmeister, Johann Philipp Kirnberger, Francesco Antonio Vallotti und Thomas Young verschiedene Wohltemperamente mit dem Ziel der Teilung geschaffen Erhöhen Sie die Kommas, um die Dissonanz der am stärksten betroffenen Intervalle zu reduzieren. Werckmeister und Kirnberger waren jeweils mit seinem ersten Temperament unzufrieden und schufen daher mehrere Temperamente, wobei die letzteren Temperamente der gleichtemperierten Temperamente näher kommen als die ersteren. Ebenso ging Europa als Ganzes allmählich von mitteltönigen und wohltemperierten Temperamenten zu 12-TEDO über, dem System, das es noch heute verwendet.
Teilmengen
Während einige Arten von Musik, wie Serialismus , verwenden alle zwölf Töne des 12-TEDO, nur die meisten Musik verwendet Notizen aus einer bestimmten Untergruppe von 12-TEDO als Maßstab bekannt. Es gibt viele verschiedene Arten von Waagen.
Der beliebteste Waagentyp in 12-TEDO ist Mittelton. Mittelton bezieht sich auf jede Tonleiter, bei der alle Noten auf dem Quintenzirkel aufeinander folgen. Mitteltonskalen unterschiedlicher Größe existieren, und einige verwendete Mitteltonskalen umfassen Fünf-Noten-Mittelton , Sieben-Noten-Mittelton und Neun-Noten-Mittelton . Meantone ist im Design westlicher Instrumente präsent. Zum Beispiel sind die Tasten eines Klaviers und seiner Vorgänger so aufgebaut, dass die weißen Tasten eine siebentönige Mitteltonskala und die schwarzen Tasten eine fünftönige Mitteltonskala bilden. Ein weiteres Beispiel ist, dass Gitarren und andere Saiteninstrumente mit mindestens fünf Saiten typischerweise so gestimmt sind, dass ihre offenen Saiten eine fünftönige Mitteltonskala bilden.
Andere Tonleitern, die in 12-TEDO verwendet werden, umfassen die aufsteigende melodische Moll-Tonleiter , die harmonische Moll-Tonleiter , die harmonische Dur- Tonleiter , die verminderte Tonleiter und die In-Tonleiter .
Siehe auch
- Gleiches Temperament
- Nur Intonation
- Musikalische Akustik (die Physik der Musik)
- Musik und Mathematik
- Mikrotonale Musik
- Liste der Mitteltonintervalle
- Diatonisch und chromatisch
- Elektronischer Tuner
- Musikalische Stimmung
Verweise
Fußnoten
Zitate
Quellen
- Barbour, James Murray (2004). Stimmung und Temperament: Ein historischer Überblick . Kuriergesellschaft. ISBN 978-0-486-43406-3.
- Benward, Bruce; Saker, Marilyn (2003). Musik in Theorie und Praxis . 1 . McGraw-Hill. ISBN 978-0-07-294261-3.
- Cho, Gene J. (2003). Die Entdeckung der musikalischen Gleichheit in China und Europa im 16. Jahrhundert . E. Mellen Press. ISBN 978-0-7734-6941-9.
- Cho, Gene J. (2010). „Die Bedeutung der Entdeckung der musikalischen Temperamentsgleichheit in der Kulturgeschichte“ . Zeitschrift des Xinghai-Konservatoriums für Musik .
- Christensen, Thomas (2002). Die Cambridge-Geschichte der westlichen Musiktheorie . Cambridge University Press. ISBN 978-0-521-62371-1.
- Cohen, H. Floris (1987). „Simon Stevins gleichmäßige Einteilung der Oktave“. Annalen der Wissenschaft . Informa UK Limited. 44 (5): 471–488. doi : 10.1080/00033798700200311 . ISSN 0003-3790 .
- de Gorzanis, G. (1981). Intabolatura di liuto: I-III . Intabolatura di liuto: I-III (auf Italienisch). Minkoff. ISBN 978-2-8266-0721-2.
- Di Veroli, Claudio (2009). Ungleiche Temperamente: Theorie, Geschichte und Praxis (2. Aufl.). Bray, Irland: Bray Barock.
- Galilei, Vincenzo (1584). Il Fronimo . Venedig: Girolamo Scotto .
- Hart, Roger (1998), Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China , Departments of History and Asian Studies, University of Texas, Austin, archiviert vom Original am 2012-03-05 , abgerufen 2012-03-20
- Jorgens, Elise Bickford (1986). Englisches Lied, 1600-1675: Faksimiles von sechsundzwanzig Manuskripten und eine Ausgabe der Texte . Girlande.
- Kuttner, Fritz A. (Mai 1975). "Prinz Chu Tsai-Yüs Leben und Werk: Eine Neubewertung seines Beitrags zur Gleichheitstheorie" (PDF) . Ethnomusikologie . 19 (2): 163–206. doi : 10.2307/850355 . JSTOR 850355 .
- Kwang-chih Chang; Pingfang-Xu; Liancheng-Lu (2005). „Der östliche Zhou und das Wachstum des Regionalismus“. Die Entstehung der chinesischen Zivilisation: Eine archäologische Perspektive . Xu Pingfang, Shao Wangping, Zhang Zhongpei, Wang Renxiang. Yale University Press. ISBN 978-0-300-09382-7.
- Lienhard, John H. (1997). "Gleichmäßiges Temperament" . Die Motoren unseres Einfallsreichtums . Universität Houston . Abgerufen 2014-10-05 .
- Moody, Richard (Februar 2003). „Frühes Temperament, eine akustische Perspektive: Claude Montal 1836“. Zeitschrift für Klaviertechniker . Kansas City.
- Needham, Joseph ; Ling, Wang; Robinson, Kenneth G. (1962). Wissenschaft und Zivilisation in China . Band 4 - Teil 1. Cambridge University Press. ISBN 978-0-521-05802-5.
- Needham, Joseph; Ronan, Colin A. (1978). Die kürzere Wissenschaft und Zivilisation in China . Band 4 - Teil 1. Cambridge University Press.
- Partch, Harry (1979). Genesis einer Musik (2. Aufl.). Da Capo-Presse. ISBN 0-306-80106-X.
- Robinson, Kenneth (1980). Eine kritische Studie über Chu Tsai-yüs Beitrag zur Theorie der gleichen Temperaments in der chinesischen Musik . Band 9 der Sinologica Coloniensia. Wiesbaden: Steiner. ISBN 978-3-515-02732-8.
- Sethares, William A. (2005). Stimmung, Timbre, Spektrum, Skala (2. Aufl.). London: Springer-Verlag. ISBN 1-85233-797-4.
- Stimmt, Timotheus (2018). „Der Kampf zwischen tadelloser Intonation und maximierter Modulation“ . Musikalische Angebote . 9 (2): 61–74. doi : 10.15385/jmo.2018.9.2.2 .
- von Helmholtz, Hermann ; Ellis, Alexander J. (1885). Zur Tonempfindung als physiologische Grundlage der Musiktheorie (2. Aufl.). London: Longmans, Grün.
- Wilson, John (1997). "Dreißig Präludien in allen (24) Tonarten für Laute [DP 49]" . Die Diapason-Presse . Abgerufen am 27. Oktober 2020 .
Weiterlesen
- Duffin, Ross W. Wie ausgeglichenes Temperament die Harmonie ruiniert (und warum Sie sich darum kümmern sollten) . WW Norton & Company, 2007.
- Jörgensen, Owen. Abstimmung . Michigan State University Press, 1991. ISBN 0-87013-290-3
- Chramow, Mykhaylo. "Approximation of 5-limit just intonation. Computer MIDI Modeling in Negative Systems of Equal Divisions of the Octave", Proceedings of the International Conference SIGMAP-2008 , 26. – 29. Juli 2008, Porto , S. 181–184, ISBN 978-989 -8111-60-9
- Surjodiningrat, W., Sudarjana, PJ, und Susanto, A. (1972) Tonmessungen herausragender javanischer Gamelans in Jogjakarta und Surakarta , Gadjah Mada University Press, Jogjakarta 1972. Zitiert auf https://web.archive.org/web/ 20050127000731/http://web.telia.com/~u57011259/pelog_main.htm . Abgerufen am 19. Mai 2006.
- Stewart, PJ (2006) "From Galaxy to Galaxy: Music of the Spheres" [1]
- Sensations of Tone ein Grundlagenwerk über Akustik und Klangwahrnehmung von Hermann von Helmholtz. Insbesondere Anhang XX: Ergänzungen des Übersetzers, Seiten 430-556, (pdf Seiten 451-577)]
Externe Links
- Xenharmonic-Wiki über EDOs vs. Equal Temperaments
- Huygens-Fokker-Stiftung Zentrum für mikrotonale Musik
- A.Orlandini: Musikakustik
- "Temperament" aus einer Ergänzung zu Mr. Chambers' Cyclopædia (1753)
- Barbieri, Patrizio. Enharmonische Instrumente und Musik, 1470–1900 Archiviert 2009-02-15 at the Wayback Machine . (2008) Latina, Il Levante Libreria Editrice
- Fraktale mikrotonale Musik , Jim Kukula .
- Alle vorhandenen Zitate aus dem 18. Jahrhundert über JS Bach und Temperament
- Dominic Eckersley: „ Rosetta Revisited: Bachs sehr gewöhnliches Temperament “
- Wohltemperamente, basierend auf der Werckmeister-Definition
- F AVORED C ARDINALITIES O F S CALES durch P ETER B UCH

![{\displaystyle \left({\sqrt[{12}]{2}}\right)^{12}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f0e94dc870dfc2af0eb35a7b362eb3776054719)
![{\displaystyle \left({\sqrt[{12}]{2}}\right)^{84}=2^{7}=128}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc85da07cabc4f33cc3fc965e9ef6e74361e7c7)



![{\displaystyle {\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)

![{\displaystyle P_{n}=P_{a}\left({\sqrt[{12}]{2}}\right)^{(na)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
![{\displaystyle P_{40}=440\left({\sqrt[{12}]{2}}\right)^{(40-49)}\approx 261,626\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{\displaystyle P_{46}=440\left({\sqrt[{12}]{2}}\right)^{(46-49)}\approx 369,994\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)