Additives weißes Gaußsches Rauschen - Additive white Gaussian noise

Additives weißes Gaußsches Rauschen ( AWGN ) ist ein grundlegendes Rauschmodell, das in der Informationstheorie verwendet wird , um den Effekt vieler zufälliger Prozesse in der Natur nachzuahmen. Die Modifikatoren bezeichnen spezifische Eigenschaften:

• Additiv, weil es zu jedem Rauschen hinzugefügt wird, das dem Informationssystem eigen sein könnte.
• Weiß bezieht sich auf die Idee, dass es für das Informationssystem eine gleichmäßige Leistung über das Frequenzband hat. Es ist eine Analogie zur Farbe Weiß, die bei allen Frequenzen im sichtbaren Spektrum gleichmäßige Emissionen aufweist .
• Gaußsch, weil es eine Normalverteilung im Zeitbereich mit einem durchschnittlichen Zeitbereichswert von Null hat.

Breitbandrauschen kommt von vielen natürlichen Rauschquellen, wie z. B. den thermischen Schwingungen von Atomen in Leitern (als thermisches Rauschen oder Johnson-Nyquist-Rauschen bezeichnet ), Schussrauschen , Schwarzkörperstrahlung von der Erde und anderen warmen Objekten sowie von Himmelsquellen wie die Sonne. Der zentrale Grenzwertsatz der Wahrscheinlichkeitstheorie zeigt, dass die Summe vieler zufälliger Prozesse tendenziell eine Verteilung aufweist, die als Gaußsch oder Normal bezeichnet wird.

AWGN wird häufig verwendet als Kanalmodell , in dem die einzige Beeinträchtigung Kommunikation eine lineare Addition von breitbandigen oder Weißrauschen mit konstanter spektralen Dichte (ausgedrückt als Watt pro Hertz der Bandbreite ) und eine Gauß'schen Verteilung der Amplitude. Das Modell berücksichtigt nicht Fading , Frequenzselektivität , Interferenz , Nichtlinearität oder Dispersion . Es werden jedoch einfache und nachvollziehbare mathematische Modelle erstellt, die nützlich sind, um einen Einblick in das zugrunde liegende Verhalten eines Systems zu erhalten, bevor diese anderen Phänomene berücksichtigt werden.

Der AWGN-Kanal ist ein gutes Modell für viele Satelliten- und Weltraumkommunikationsverbindungen. Es ist kein gutes Modell für die meisten terrestrischen Verbindungen, da Mehrweg, Geländeblockierung, Interferenz usw. Für die Modellierung terrestrischer Pfade wird AWGN jedoch häufig verwendet, um Hintergrundgeräusche des untersuchten Kanals zu simulieren, zusätzlich zu Mehrweg, Geländeblockierung, Interferenzen, Bodenstörungen und Selbststörungen, denen moderne Funksysteme im terrestrischen Betrieb begegnen.

Kanalkapazität

Der AWGN-Kanal wird durch eine Reihe von Ausgängen mit einem zeitdiskreten Ereignisindex dargestellt . ist die Summe des Eingangs und Lärm, gegebenen ist unabhängig und identisch verteilt von einem Mittelwert von Null und gezogenen Normalverteilung mit Varianz (das Rauschen). Es wird weiterhin angenommen, dass die nicht mit dem korrelieren . ${\ displaystyle Y_ {i}}$${\ displaystyle i}$${\ displaystyle Y_ {i}}$${\ displaystyle X_ {i}}$${\ displaystyle Z_ {i}}$${\ displaystyle Z_ {i}}$ ${\ displaystyle N}$${\ displaystyle Z_ {i}}$${\ displaystyle X_ {i}}$

${\ displaystyle Z_ {i} \ sim {\ mathcal {N}} (0, N) \, \!}$

${\ displaystyle Y_ {i} = X_ {i} + Z_ {i}. \, \!}$

Die Kapazität des Kanals ist unendlich, es sei denn, das Rauschen ist ungleich Null und die sind ausreichend eingeschränkt. Die häufigste Einschränkung für die Eingabe ist die sogenannte "Leistungs" -Einschränkung, die erfordert, dass für ein über den Kanal übertragenes Codewort Folgendes gilt: ${\ displaystyle N}$${\ displaystyle X_ {i}}$${\ displaystyle (x_ {1}, x_ {2}, \ dots, x_ {k})}$

${\ displaystyle {\ frac {1} {k}} \ sum _ {i = 1} ^ {k} x_ {i} ^ {2} \ leq P,}$

Dabei steht die maximale Kanalleistung. Daher ist die Kanalkapazität für den leistungsbeschränkten Kanal gegeben durch: ${\ displaystyle P}$

${\ displaystyle C = \ max _ {f (x) {\ text {st}} E \ left (X ^ {2} \ right) \ leq P} I (X; Y) \, \!}$

Wo ist die Verteilung von . Erweitern Sie und schreiben Sie es in Bezug auf die Differentialentropie : ${\ displaystyle f (x)}$${\ displaystyle X}$${\ displaystyle I (X; Y)}$

${\ Anzeigestil {\ begin {ausgerichtet} I (X; Y) = h (Y) -h (Y | X) & = h (Y) -h (X + Z | X) & = h (Y) -h (Z | X) \ end {align}} \, \!}$

Aber und sind deshalb unabhängig: ${\ displaystyle X}$${\ displaystyle Z}$

${\ Anzeigestil I (X; Y) = h (Y) -h (Z) \, \!}$

Die Bewertung der Differentialentropie eines Gaußschen ergibt:

${\ displaystyle h (Z) = {\ frac {1} {2}} \ log (2 \ pi eN) \, \!}$

Weil und unabhängig sind und ihre Summe ergibt : ${\ displaystyle X}$${\ displaystyle Z}$${\ displaystyle Y}$

${\ Anzeigestil E (Y ^ {2}) = E ((X + Z) ^ {2}) = E (X ^ {2}) + 2E (X) E (Z) + E (Z ^ {2} ) \ leq P + N \, \!}$

Aus dieser Grenze schließen wir aus einer Eigenschaft der Differentialentropie, dass

${\ displaystyle h (Y) \ leq {\ frac {1} {2}} \ log (2 \ pi e (P + N)) \, \!}$

Daher ist die Kanalkapazität durch die höchste erreichbare Grenze der gegenseitigen Information gegeben :

${\ displaystyle I (X; Y) \ leq {\ frac {1} {2}} \ log (2 \ pi e (P + N)) - {\ frac {1} {2}} \ log (2 \ pi eN) \, \!}$

Wo wird maximiert, wenn: ${\ displaystyle I (X; Y)}$

${\ displaystyle X \ sim {\ mathcal {N}} (0, P) \, \!}$

Somit ist die Kanalkapazität für den AWGN-Kanal gegeben durch: ${\ displaystyle C}$

${\ displaystyle C = {\ frac {1} {2}} \ log \ left (1 + {\ frac {P} {N}} \ right) \, \!}$

Kanalkapazität und Kugelpackung

Angenommen, wir senden Nachrichten über den Kanal mit einem Index von bis , der Anzahl der verschiedenen möglichen Nachrichten. Wenn wir die Nachrichten in Bits codieren , definieren wir die Rate als: ${\ displaystyle 1}$${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle R}$

${\ displaystyle R = {\ frac {\ log M} {n}} \, \!}$

Eine Rate soll erreichbar sein, wenn es eine Folge von Codes gibt, so dass die maximale Fehlerwahrscheinlichkeit gegen Null gegen Null tendiert . Die Kapazität ist die höchste erreichbare Rate. ${\ displaystyle n}$${\ displaystyle C}$

Betrachten Sie ein Codewort der Länge, das über den AWGN-Kanal mit Rauschpegel gesendet wird . Beim Empfang ist die Varianz des Codewortvektors jetzt und ihr Mittelwert ist das gesendete Codewort. Es ist sehr wahrscheinlich, dass der Vektor in einer Kugel mit einem Radius um das gesendete Codewort enthalten ist. Wenn wir dekodieren, indem wir jede empfangene Nachricht auf das Codewort in der Mitte dieser Kugel abbilden, tritt ein Fehler nur dann auf, wenn sich der empfangene Vektor außerhalb dieser Kugel befindet, was sehr unwahrscheinlich ist. ${\ displaystyle n}$${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle {\ sqrt {n (N + \ epsilon)}}}$

Jedem Codewortvektor ist eine Kugel von empfangenen Codewortvektoren zugeordnet, die zu ihm decodiert werden, und jede solche Kugel muss eindeutig auf ein Codewort abgebildet werden. Da sich diese Kugeln daher nicht schneiden dürfen, stehen wir vor dem Problem der Kugelpackung . Wie viele verschiedene Codewörter können wir in unseren -bit-Codewortvektor packen ? Die empfangenen Vektoren haben eine maximale Energie von und müssen daher eine Kugel mit Radius einnehmen . Jede Codewortkugel hat einen Radius . Das Volumen einer n- dimensionalen Kugel ist direkt proportional zu , sodass die maximale Anzahl eindeutig dekodierbarer Kugeln, die mit der Übertragungsleistung P in unsere Kugel gepackt werden können, beträgt: ${\ displaystyle n}$${\ displaystyle n (P + N)}$${\ displaystyle {\ sqrt {n (P + N)}}}$${\ displaystyle {\ sqrt {nN}}}$${\ displaystyle r ^ {n}}$

${\ displaystyle {\ frac {(n (P + N)) ^ {\ frac {n} {2}} {(nN) ^ {\ frac {n} {2}}} = 2 ^ {{\ frac {n} {2}} \ log (1 + P / N)} \, \!}$

Durch dieses Argument kann die Rate R nicht mehr als sein . ${\ displaystyle {\ frac {1} {2}} \ log (1 + P / N)}$

Erreichbarkeit

In diesem Abschnitt zeigen wir die Erreichbarkeit der Obergrenze für die Rate aus dem letzten Abschnitt.

Ein Codebuch, das sowohl dem Codierer als auch dem Decodierer bekannt ist, wird durch Auswahl von Codewörtern der Länge n, iid Gauß mit Varianz und Mittelwert Null, erzeugt. Für großes n liegt die empirische Varianz des Codebuchs sehr nahe an der Varianz seiner Verteilung, wodurch eine Verletzung der Leistungsbeschränkung wahrscheinlich vermieden wird. ${\ displaystyle P- \ epsilon}$

Empfangene Nachrichten werden in eine Nachricht im Codebuch dekodiert, die eindeutig gemeinsam typisch ist. Wenn es keine solche Nachricht gibt oder wenn die Leistungsbeschränkung verletzt wird, wird ein Decodierungsfehler deklariert.

Lassen Sie das Codewort für die Nachrichten bezeichnen , während ist, wie vor dem empfangenen Vektor. Definieren Sie die folgenden drei Ereignisse: ${\ displaystyle X ^ {n} (i)}$${\ displaystyle i}$${\ displaystyle Y ^ {n}}$

1. Ereignis : Die Leistung der empfangenen Nachricht ist größer als . ${\ displaystyle U}$${\ displaystyle P}$
2. Ereignis : Die gesendeten und empfangenen Codewörter sind nicht gemeinsam typisch. ${\ displaystyle V}$
3. Ereignis : ist in , den typischen Satz , wo , was zu sagen ist , dass das falsche Codewort mit dem empfangenen Vektor gemeinsam typisch ist. ${\ displaystyle E_ {j}}$${\ displaystyle (X ^ {n} (j), Y ^ {n})}$${\ displaystyle A _ {\ epsilon} ^ {(n)}}$${\ displaystyle i \ neq j}$

Ein Fehler tritt auf, wenn also , oder einer der auftreten. Nach dem Gesetz der großen Zahlen geht es gegen Null, wenn sich n der Unendlichkeit nähert, und nach der gemeinsamen Eigenschaft der asymptotischen Äquipartition gilt das Gleiche für . Daher sind für eine ausreichend große beide und jeweils kleiner als . Da und unabhängig sind , haben wir das und sind auch unabhängig. Daher durch die gemeinsame AEP , . Dies ermöglicht es uns , die Fehlerwahrscheinlichkeit wie folgt zu berechnen : ${\ displaystyle U}$${\ displaystyle V}$${\ displaystyle E_ {i}}$${\ displaystyle P (U)}$${\ displaystyle P (V)}$${\ displaystyle n}$${\ displaystyle P (U)}$${\ displaystyle P (V)}$${\ displaystyle \ epsilon}$${\ displaystyle X ^ {n} (i)}$${\ displaystyle X ^ {n} (j)}$${\ displaystyle i \ neq j}$${\ displaystyle X ^ {n} (i)}$${\ displaystyle Y ^ {n}}$${\ displaystyle P (E_ {j}) = 2 ^ {- n (I (X; Y) -3 \ epsilon)}}$${\ displaystyle P_ {e} ^ {(n)}}$

${\ displaystyle {\ begin {align} P_ {e} ^ {(n)} & \ leq P (U) + P (V) + \ sum _ {j \ neq i} P (E_ {j}) \\ & \ leq \ epsilon + \ epsilon + \ sum _ {j \ neq i} 2 ^ {- n (I (X; Y) -3 \ epsilon)} \\ & \ leq 2 \ epsilon + (2 ^ {nR } -1) 2 ^ {- n (I (X; Y) -3 \ epsilon)} \\ & \ leq 2 \ epsilon + (2 ^ {3n \ epsilon}) 2 ^ {- n (I (X; Y) -R)} \\ & \ leq 3 \ epsilon \ end {align}}}$

Wenn sich n der Unendlichkeit nähert, geht es daher auf Null und . Daher gibt es einen Code der Rate R, der willkürlich nahe an der zuvor abgeleiteten Kapazität liegt. ${\ displaystyle P_ {e} ^ {(n)}}$${\ displaystyle R <I (X; Y) -3 \ epsilon}$

Codierungssatz umgekehrt

Hier zeigen wir, dass Raten über der Kapazität nicht erreichbar sind. ${\ displaystyle C = {\ frac {1} {2}} \ log (1 + {\ frac {P} {N}})}$

Angenommen, die Leistungsbeschränkung für ein Codebuch ist erfüllt, und es wird ferner angenommen, dass die Nachrichten einer gleichmäßigen Verteilung folgen. Sei die Eingangsnachricht und die Ausgangsnachricht. Somit fließen die Informationen wie folgt: ${\ displaystyle W}$${\ displaystyle {\ hat {W}}}$

${\ displaystyle W \ longrightarrow X ^ {(n)} (W) \ longrightarrow Y ^ {(n)} \ longrightarrow {\ hat {W}}}$

Die Ausnutzung der Ungleichung von Fano ergibt:

${\ displaystyle H (W | {\ hat {W}}) \ leq 1 + nRP_ {e} ^ {(n)} = n \ epsilon _ {n}}$ wo als ${\ displaystyle \ epsilon _ {n} \ rightarrow 0}$${\ displaystyle P_ {e} ^ {(n)} \ rightarrow 0}$

Sei die codierte Nachricht des Codewortindex i. Dann: ${\ displaystyle X_ {i}}$

${\ displaystyle {\ begin {align} nR & = H (W) \\ & = I (W; {\ hat {W}}) + H (W | {\ hat {W}}) \\ & \ leq I. (W; {\ hat {W}}) + n \ epsilon _ {n} \\ & \ leq I (X ^ {(n)}; Y ^ {(n)}) + n \ epsilon _ {n} \\ & = h (Y ^ {(n)}) - h (Y ^ {(n)} | X ^ {(n)}) + n \ epsilon _ {n} \\ & = h (Y ^ { (n)}) - h (Z ^ {(n)}) + n \ epsilon _ {n} \\ & \ leq \ sum _ {i = 1} ^ {n} h (Y_ {i}) - h (Z ^ {(n)}) + n \ epsilon _ {n} \\ & \ leq \ sum _ {i = 1} ^ {n} I (X_ {i}; Y_ {i}) + n \ epsilon _ {n} \ end {align}}}$

Sei die durchschnittliche Potenz des Codeworts des Index i: ${\ displaystyle P_ {i}}$

${\ displaystyle P_ {i} = {\ frac {1} {2 ^ {nR}}} \ sum _ {w} x_ {i} ^ {2} (w) \, \!}$

Wobei die Summe über allen Eingabenachrichten liegt . und sind unabhängig, daher ist die Erwartung der Leistung von für den Geräuschpegel : ${\ displaystyle w}$${\ displaystyle X_ {i}}$${\ displaystyle Z_ {i}}$${\ displaystyle Y_ {i}}$${\ displaystyle N}$

${\ displaystyle E (Y_ {i} ^ {2}) = P_ {i} + N \, \!}$

Und wenn es normal verteilt ist, haben wir das ${\ displaystyle Y_ {i}}$

${\ displaystyle h (Y_ {i}) \ leq {\ frac {1} {2}} \ log {2 \ pi e} (P_ {i} + N) \, \!}$

Deshalb,

${\ displaystyle {\ begin {align} nR & \ leq \ sum (h (Y_ {i}) - h (Z_ {i})) + n \ epsilon _ {n} \\ & \ leq \ sum \ left ({ \ frac {1} {2}} \ log (2 \ pi e (P_ {i} + N)) - {\ frac {1} {2}} \ log (2 \ pi eN) \ right) + n \ epsilon _ {n} \\ & = \ sum {\ frac {1} {2}} \ log (1 + {\ frac {P_ {i}} {N}}) + n \ epsilon _ {n} \ end {ausgerichtet}}}$

Wir können Jensens Gleichheit auf eine konkave (abwärts gerichtete) Funktion von x anwenden, um Folgendes zu erhalten: ${\ displaystyle \ log (1 + x)}$

${\ displaystyle {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} {\ frac {1} {2}} \ log \ left (1 + {\ frac {P_ {i} } {N}} \ rechts) \ leq {\ frac {1} {2}} \ log \ links (1 + {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} { \ frac {P_ {i}} {N}} \ right) \, \!}$

Da jedes Codewort einzeln die Leistungsbeschränkung erfüllt, erfüllt der Durchschnitt auch die Leistungsbeschränkung. Deshalb,

${\ displaystyle {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} {\ frac {P_ {i}} {N}} \, \!}$

Was wir anwenden können, um die obige Ungleichung zu vereinfachen und zu erhalten:

${\ displaystyle {\ frac {1} {2}} \ log \ left (1 + {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} {\ frac {P_ {i} } {N}} \ rechts) \ leq {\ frac {1} {2}} \ log \ links (1 + {\ frac {P} {N}} \ rechts) \, \!}$

Deshalb muss es das sein . Daher muss R kleiner sein als ein Wert, der willkürlich nahe an der zuvor abgeleiteten Kapazität liegt, wie z . ${\ displaystyle R \ leq {\ frac {1} {2}} \ log \ left (1 + {\ frac {P} {N}} \ right) + \ epsilon _ {n}}$${\ displaystyle \ epsilon _ {n} \ rightarrow 0}$

Auswirkungen im Zeitbereich

Nulldurchgänge eines lauten Kosinus

Bei der seriellen Datenkommunikation wird das mathematische AWGN-Modell verwendet, um den durch Zufallsjitter (RJ) verursachten Zeitsteuerungsfehler zu modellieren .

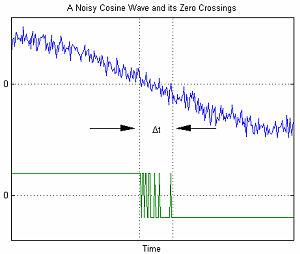
Die Grafik rechts zeigt ein Beispiel für Zeitfehler, die mit AWGN verbunden sind. Die Variable Δ t stellt die Unsicherheit in dem Nulldurchgang. Wenn die Amplitude des AWGN erhöht wird, nimmt das Signal-Rausch-Verhältnis ab. Dies führt zu einer erhöhten Unsicherheit Δ t .

Bei Beeinflussung durch AWGN beträgt die durchschnittliche Anzahl von positiv oder negativ verlaufenden Nulldurchgängen pro Sekunde am Ausgang eines Schmalbandpassfilters, wenn der Eingang eine Sinuswelle ist

${\ displaystyle {\ frac {\ text {positive Nulldurchgänge}} {\ text {second}}} = {\ frac {\ text {negative Nulldurchgänge}} {\ text {second}}}}$

${\ displaystyle \ quad = f_ {0} {\ sqrt {\ frac {{\ text {SNR}} + 1 + {\ frac {B ^ {2}} {12f_ {0} ^ {2}}} { {\ text {SNR}} + 1}}},}$

wo

f ₀ = die Mittenfrequenz des Filters,

B = Filterbandbreite,

SNR = lineares Signal-Rausch-Leistungsverhältnis.

Effekte in der Zeigerdomäne

AWGN-Beiträge im Zeigerbereich

In modernen Kommunikationssystemen kann bandbegrenztes AWGN nicht ignoriert werden. Wenn AWGN in der Bandbegrenzung Modellieren Phasor Domäne, zeigt eine statistische Analyse , dass die Amplituden der realen und imaginären Beiträge unabhängigen Variablen sind , die die folgen Gauß - Verteilung Modell. In Kombination ist die Größe des resultierenden Zeigers eine Rayleigh-verteilte Zufallsvariable, während die Phase gleichmäßig von 0 bis 2π verteilt ist.

Die Grafik rechts zeigt ein Beispiel dafür, wie bandbegrenztes AWGN ein kohärentes Trägersignal beeinflussen kann. Die momentane Antwort des Rauschvektors kann nicht genau vorhergesagt werden, jedoch kann seine zeitgemittelte Antwort statistisch vorhergesagt werden. Wie in der Grafik gezeigt, sagen wir zuversichtlich voraus, dass sich der Rauschzeiger ungefähr 38% der Zeit innerhalb des 1σ-Kreises, ungefähr 86% der Zeit innerhalb des 2σ-Kreises und ungefähr 98% der Zeit innerhalb des 3σ-Kreises befindet.

Siehe auch

• Bodensprung
• Noisy-Channel-Codierungssatz
• Gaußscher Prozess

Verweise