Affine symmetrische Gruppe - Affine symmetric group

Die affinen symmetrischen Gruppen sind eine Familie mathematischer Strukturen, die die Symmetrien des Zahlenstrahls und die regelmäßige dreieckige Kachelung der Ebene sowie verwandte höherdimensionale Objekte beschreiben. Jede ist eine unendliche Erweiterung einer endlichen symmetrischen Gruppe , der Gruppe von Permutationen (Umlagerungen) einer endlichen Menge. Zusätzlich zu ihrer geometrischen Beschreibung können die affinen symmetrischen Gruppen als Sammlungen von Permutationen der ganzen Zahlen (..., −2, −1, 0, 1, 2, ...) definiert werden, die in gewissem Sinne periodisch sind, oder rein algebraisch als Gruppe mit bestimmten Generatoren und Relationen . Diese unterschiedlichen Definitionen ermöglichen die Erweiterung vieler wichtiger Eigenschaften der endlichen symmetrischen Gruppen auf die unendliche Umgebung und werden als Teil der Bereiche Kombinatorik und Darstellungstheorie untersucht .

Definitionen

Die affine symmetrische Gruppe kann äquivalent als abstrakte Gruppe durch Generatoren und Relationen oder in Bezug auf konkrete geometrische und kombinatorische Modelle definiert werden.

Algebraische Definition

Eine Möglichkeit, Gruppen zu definieren, sind Generatoren und Relationen . In dieser Art von Definition sind Generatoren eine Untermenge von Gruppenelementen, die, wenn sie kombiniert werden, alle anderen Elemente erzeugen. Die Beziehungen der Definition sind ein Gleichungssystem, das von den Elementen erfüllt wird, die alle anderen Gleichungen implizieren, die sie erfüllen. Auf diese Weise wird die affine symmetrische Gruppe von einer Menge erzeugt ${\displaystyle {\widetilde{S}}_{n}}$

von n Elementen, die die folgenden Beziehungen erfüllen: when , ${\displaystyle n\geq 3}$

1. ${\displaystyle s_{i}^{2}=1}$(die Generatoren sind Involutionen ),
2. ${\displaystyle s_{i}s_{j}=s_{j}s_{i}}$wenn j nicht einer von ist , was anzeigt, dass für diese Generatorpaare die Gruppenoperation kommutativ ist , und${\displaystyle i-1,i,i+1}$
3. ${\displaystyle s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}}$.

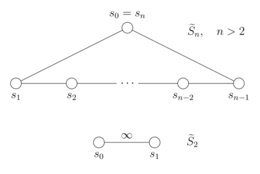
In den obigen Relationen werden Indizes modulo n genommen , so dass die dritte Relation als Sonderfall einschließt . (Die zweite und dritte Beziehung werden manchmal als Geflechtbeziehungen bezeichnet .) Wenn die affine symmetrische Gruppe die unendliche Diedergruppe ist, die von zwei Elementen erzeugt wird, die nur den Beziehungen unterliegen . ${\displaystyle s_{0}s_{n-1}s_{0}=s_{n-1}s_{0}s_{n-1}}$${\displaystyle n=2}$${\displaystyle {\widetilde{S}}_{2}}$${\displaystyle s_{0},s_{1}}$${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$

Diese Beziehungen können in die spezielle Form umgeschrieben werden, die die Coxeter-Gruppen definiert , so dass die affinen symmetrischen Gruppen Coxeter-Gruppen sind, mit deren Coxeter-Erzeugungsmengen. Für ist das Coxeter-Dynkin-Diagramm von der n- Zyklus, während es für es aus zwei Knoten besteht, die durch eine mit bezeichnete Kante verbunden sind . In diesen Diagrammen stellen die Scheitelpunkte die Generatoren dar, die für Coxeter-Gruppen Involutionen sein müssen. Die Flanken des Zyklus entsprechen den Beziehungen zwischen Paaren aufeinanderfolgender Generatoren, während das Fehlen einer Flanke zwischen anderen Generatorpaaren anzeigt, dass sie kommutieren. ${\displaystyle s_{i}}$${\displaystyle n\geq 3}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle n=2}$${\displaystyle\infty}$

Geometrische Definition

Im Euklidischen Raum mit Koordinaten bildet die Menge V von Punkten für die eine (Hyper-)Ebene , einen ( n − 1) -dimensionalen Unterraum. Für jedes Paar verschiedener Elemente i und j von und jede ganze Zahl k bildet die Menge der Punkte in V , die erfüllen, einen ( n − 2) -dimensionalen Unterraum innerhalb von V , und es gibt eine eindeutige Spiegelung von V , die diesen Unterraum fixiert. Dann kann die affine symmetrische Gruppe geometrisch als eine Sammlung von Abbildungen von V zu sich selbst realisiert werden, die Zusammensetzungen dieser Spiegelungen. ${\displaystyle \mathbb{R} ^{n}}$${\displaystyle (x_{1},\ldots,x_{n})}$${\displaystyle x_{1}+x_{2}+\ldots +x_{n}=0}$${\displaystyle \{1,\ldots,n\}}$${\displaystyle x_{i}-x_{j}=k}$

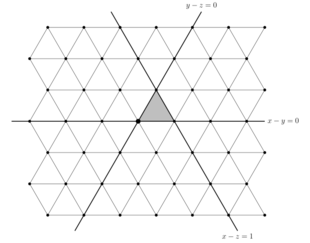
Innerhalb V bildet die Teilmenge von Punkten mit ganzzahligen Koordinaten , die den Typ A Wurzelgitter , Λ . Es ist die Menge aller ganzzahligen Vektoren, so dass . Jede Reflexion behält dieses Gitter bei, und so wird das Gitter von der gesamten Gruppe beibehalten. Tatsächlich kann man die Gruppe der starren Transformationen von V definieren , die das Gitter Λ erhalten . ${\displaystyle (a_{1},\ldots,a_{n})}$${\displaystyle a_{1}+\ldots +a_{n}=0}$${\displaystyle {\widetilde{S}}_{n}}$

Die festen Unterräume dieser Spiegelungen unterteilen V in kongruente Simplizes , sogenannte Alkoven . Die Situation ist in der Abbildung dargestellt; In diesem Fall ist das Wurzelgitter ein dreieckiges Gitter, das durch reflektierende Linien in gleichseitige Dreiecksnischen unterteilt wird. Für höhere Dimensionen sind die Nischen jedoch keine regulären Simplizes. ${\displaystyle n=3}$

Um zwischen den geometrischen und algebraischen Definitionen zu übersetzen, fixieren Sie eine Nische und betrachten Sie die n Hyperebenen, die ihre Grenze bilden. Die Reflexionen durch diese Grenzhyperebenen können mit den Coxeter-Generatoren identifiziert werden. Insbesondere gibt es eine einzigartige Nische (die fundamentale Nische ), die aus solchen Punkten besteht , die durch die Hyperebenen , , ..., und begrenzt wird , wie im Fall dargestellt . Denn man kann die Reflexion durch den Coxeter-Generator identifizieren, und auch die Reflexion durch den Generator . ${\displaystyle (x_{1},\ldots,x_{n})}$${\displaystyle x_{1}\geq x_{2}\geq \dots \geq x_{n}\geq x_{1}-1}$${\displaystyle x_{1}-x_{2}=0}$${\displaystyle x_{2}-x_{3}=0}$${\displaystyle x_{1}-x_{n}=1}$${\displaystyle n=3}$${\displaystyle i=1,\ldots,n-1}$${\displaystyle x_{i}-x_{i+1}=0}$${\displaystyle s_{i}}$${\displaystyle x_{1}-x_{n}=1}$${\displaystyle s_{0}=s_{n}}$

Kombinatorische Definition

Die Elemente der affinen symmetrischen Gruppe können als eine Gruppe periodischer Permutationen der ganzen Zahlen realisiert werden. Sagen wir insbesondere, dass eine Funktion eine affine Permutation ist, wenn ${\displaystyle u\colon\mathbb{Z}\to\mathbb{Z}}$

• es ist eine Bijektion (jede ganze Zahl erscheint als der Wert von für genau eins ),${\displaystyle u(x)}$${\displaystyle x}$
• ${\displaystyle u(x+n)=u(x)+n}$für alle ganzen Zahlen x (die Funktion ist unter Verschiebung um äquivariant ), und${\displaystyle n}$
• ${\displaystyle u(1)+u(2)+\ldots +u(n)=1+2+\ldots +n}$, die th Dreieckszahl .${\displaystyle n}$

Für jede affine Permutation und allgemeiner für jede verschiebungsäquivalente Bijektion müssen die Zahlen alle unterschiedlich modulo n sein . Eine affine Permutation wird durch ihre Fensternotation eindeutig bestimmt , da alle anderen Werte von durch Verschieben dieser Werte gefunden werden können. Somit können affine Permutationen auch mit Tupeln von ganzen Zahlen identifiziert werden , die ein Element aus jeder Kongruenzklasse modulo n enthalten und zu summieren . ${\displaystyle u(1),\ldots,u(n)}$ ${\displaystyle [u(1),\ldots,u(n)]}$${\displaystyle u}$${\displaystyle [u(1),\ldots,u(n)]}$${\displaystyle 1+2+\ldots +n}$

Um zwischen den kombinatorischen und algebraischen Definitionen zu übersetzen, kann man den Coxeter-Generator mit der affinen Permutation identifizieren, die die Fensternotation hat , und auch den Generator mit der affinen Permutation identifizieren . Allgemeiner kann jede Spiegelung (d. h. eine Konjugierte eines der Coxeter-Generatoren) wie folgt eindeutig beschrieben werden: für verschiedene ganze Zahlen i , j in und beliebige ganze k , bildet sie i auf j − kn ab , bildet j auf i + . ab kn und fixiert alle Eingaben, die nicht zu i oder j modulo n kongruent sind . (In Bezug auf die geometrische Definition entspricht dies der Spiegelung über die Ebene . Die Entsprechung zwischen der geometrischen und kombinatorischen Darstellung für andere Elemente wird in § Zusammenhang zwischen der geometrischen und kombinatorischen Definition diskutiert .) ${\displaystyle i=1,\ldots,n-1}$${\displaystyle s_{i}}$${\displaystyle [1,2,\ldots,i-1,i+1,i,i+2,\ldots,n]}$${\displaystyle s_{0}=s_{n}}$${\displaystyle [0,2,3,\ldots ,n-2,n-1,n+1]}$${\displaystyle \{1,\ldots,n\}}$${\displaystyle x_{i}-x_{j}=k}$

Darstellung als Matrizen

Man kann affine Permutationen als unendliche periodische Permutationsmatrizen darstellen . Wenn eine affine Permutation ist, platziert man den Eintrag 1 an Position im unendlichen Gitter für jede ganze Zahl i , und alle anderen Einträge sind gleich 0. Da u eine Bijektion ist, enthält die resultierende Matrix genau eine 1 in jeder Zeile und Spalte. Die Periodizitätsbedingung auf der Karte u stellt sicher, dass der Eintrag bei Position für jedes Paar von ganzen Zahlen gleich dem Eintrag bei Position ist . In der Abbildung ist beispielsweise ein Teil der Matrix für die affine Permutation dargestellt, mit den Konventionen, dass 1s durch • ersetzt werden, 0s weggelassen werden, Zeilennummern von oben nach unten steigen, Spaltennummern von links nach rechts steigen und die Grenze des Kastens bestehend aus Zeilen und Spalten 1, 2, 3 gezeichnet. ${\displaystyle u:\mathbb{Z}\to\mathbb{Z}}$${\displaystyle (i,u(i))}$${\displaystyle \mathbb{Z} \times \mathbb{Z}}$${\displaystyle (a,b)}$${\displaystyle (a+n,b+n)}$${\displaystyle (a,b)}$${\displaystyle [2,0,4]\in {\widetilde{S}}_{3}}$

Beziehung zur endlichen symmetrischen Gruppe

Die affine symmetrische Gruppe enthält die endliche symmetrische Gruppe von Permutationen auf Elementen sowohl als Untergruppe als auch als Quotientengruppe . ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle n}$

Als Untergruppe

Es gibt einen kanonischen Weg, eine Untergruppe zu wählen , die isomorph zur endlichen symmetrischen Gruppe ist . Im Sinne der algebraischen Definition ist dies die Untergruppe von erzeugt durch (ohne die einfache Reflexion ). Geometrisch entspricht dies der Untergruppe von Transformationen, die den Ursprung fixieren, während es kombinatorisch den Fensternotationen entspricht , bei denen die Fensternotation also die einzeilige Notation einer endlichen Permutation ist. ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle s_{1},\ldots,s_{n-1}}$${\displaystyle s_{0}=s_{n}}$${\displaystyle \{u(1),\ldots,u(n)\}=\{1,2,\ldots,n\}}$

Wenn die Fensternotation eines Elements dieser Standardkopie von ist , ist seine Wirkung auf die Hyperebene V in durch die Permutation der Koordinaten gegeben: . (In diesem Artikel ist die geometrische Wirkung von Permutationen und affinen Permutationen auf der rechten Seite; wenn u und v also zwei affine Permutationen sind, wird die Wirkung von uv auf einen Punkt dadurch gegeben, dass zuerst u und dann v angewendet werden .) ${\displaystyle u=[u(1),u(2),\ldots,u(n)]}$${\displaystyle S_{n}\subset {\widetilde{S}}_{n}}$${\displaystyle \mathbb{R} ^{n}}$${\displaystyle (x_{1},x_{2},\ldots ,x_{n})\cdot u=(x_{u(1)},x_{u(2)},\ldots ,x_{u( n)})}$

Es gibt auch viele nicht standardmäßige Kopien von in . Eine geometrische Konstruktion besteht darin, einen beliebigen Punkt a in auszuwählen ( dh einen ganzzahligen Vektor, dessen Koordinaten sich zu 0 summieren); die Untergruppe der Isometrien, die a fixieren, ist isomorph zu . Die analoge kombinatorischen Konstruktion ist jede Teilmenge wählen A der , daß ein Element aus jeder Konjugationsklasse modulo enthält n und deren Elemente Summe ; die Untergruppe der affinen Permutationen, die A stabilisieren, ist isomorph zu . ${\displaystyle S_{n}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle ({\widetilde{S}}_{n})_{a}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle \mathbb{Z}}$${\displaystyle 1+2+\ldots +n}$${\displaystyle ({\widetilde{S}}_{n})_{A}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle S_{n}}$

Als Quotient

Es gibt eine einfache Abbildung (technisch ein surjektiver Gruppenhomomorphismus ) π von auf die endliche symmetrische Gruppe . Hinsichtlich der kombinatorischen Definition kann eine affine Permutation auf eine Permutation abgebildet werden, indem die Fenstereinträge modulo n auf Elemente von reduziert werden , wobei die einzeilige Notation einer Permutation verbleibt. Das Bild einer affinen Permutation u wird als zugrundeliegende Permutation von u bezeichnet . ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle \{1,2,\ldots,n\}}$${\displaystyle \pi(u)}$

Die Karte & pgr den Coxeter Generator sendet an die Permutation deren einzeilige Notation und Zyklus - Notation ist und jeweils. In Bezug auf die Coxeter-Generatoren von kann dies geschrieben werden als${\displaystyle s_{0}=[0,2,3,4,\ldots ,n-2,n-1,n+1]}$${\displaystyle [n,2,3,4,\ldots,n-2,n-1,1]}$${\displaystyle (1\;n)}$${\displaystyle S_{n}}$${\displaystyle \pi(s_{0})=s_{1}s_{2}\cdots s_{n-2}s_{n-1}s_{n-2}\cdots s_{2}s_{1} .}$

Der Kern von π ist per Definition die Menge affiner Permutationen, deren zugrundeliegende Permutation die Identität ist . Die Fensternotationen solcher affiner Permutationen haben die Form , wobei ein ganzzahliger Vektor ist , dh . Geometrisch besteht dieser Kern aus den Translationen , also den Isometrien, die den gesamten Raum V verschieben, ohne ihn zu drehen oder zu reflektieren. In einem Missbrauch der Notation wird das Symbol Λ in diesem Artikel für alle drei dieser Mengen verwendet (Ganzzahlvektoren in V , affine Permutationen mit zugrunde liegender Permutation der Identität und Übersetzungen); in allen drei Einstellungen verwandelt die natürliche Gruppenoperation Λ in eine abelsche Gruppe , frei generiert durch die n − 1 Vektoren . ${\displaystyle [1-a_{1}\cdot n,2-a_{2}\cdot n,\ldots ,n-a_{n}\cdot n]}$${\displaystyle (a_{1},a_{2},\ldots,a_{n})}$${\displaystyle a_{1}+a_{2}+\ldots +a_{n}=0}$${\displaystyle (a_{1},\ldots,a_{n})\in\Lambda}$${\displaystyle \{(1,-1,0,\ldots ,0),(0,1,-1,\ldots ,0),\ldots ,(0,\ldots ,0,1,-1)\ }}$

Die Beziehung zwischen dem Kern, der affinen symmetrischen Gruppe und das Bild von π kann durch die ausgedrückt werden kurze exakte Sequenz . Hier ist der Kernel, eine freie abelsche Gruppe mit n − 1 Generatoren. ${\displaystyle 0\to\mathbb{Z}^{n-1}\to {\widetilde{S}}_{n}\mathop {\overset {\pi}{\to}} S_{n}\to 0}$${\displaystyle\mathbb{Z}^{n-1}\cong\Lambda}$

Zusammenhang zwischen geometrischen und kombinatorischen Definitionen

Die affine symmetrische Gruppe hat Λ als normale Untergruppe und ist isomorph zum halbdirekten Produkt${\displaystyle {\widetilde{S}}_{n}}$

dieser Untergruppe mit der endlichen symmetrischen Gruppe , wobei die Wirkung von auf Λ durch Permutation von Koordinaten erfolgt. Folglich hat jedes Element u von eine einzigartige Realisierung als Produkt, wobei eine Permutation in der Standardkopie von in und eine Übersetzung in ist . ${\displaystyle S_{n}}$${\displaystyle S_{n}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle u=r\cdot t}$${\displaystyle r}$${\displaystyle S_{n}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle t}$${\displaystyle \Lambda}$

Dieser Gesichtspunkt erlaubt eine direkte Übersetzung zwischen den kombinatorischen und geometrischen Definitionen von : schreibt man wo und dann entspricht die affine Permutation

u der starren Bewegung von V definiert durch ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle [u(1),\ldots ,u(n)]=[r_{1}-a_{1}\cdot n,\ldots ,r_{n}-a_{n}\cdot n]}$${\displaystyle r=[r_{1},\ldots,r_{n}]=\pi(u)}$${\displaystyle (a_{1},a_{2},\ldots,a_{n})\in\Lambda}$

$${\displaystyle (x_{1},\ldots,x_{n})\cdot u=\left(x_{r(1)}+a_{1},\ldots,x_{r(n)}+a_{ n}\rechts).}$$

Darüber hinaus wirkt die affine symmetrische Gruppe wie jede affine Coxeter-Gruppe transitiv und frei auf die Menge der Alkoven: Für jeweils zwei Alkoven führt ein einzigartiges Gruppenelement einen Alkoven zum anderen. Daher kann man durch eine willkürliche Wahl der Nische die Gruppe in eine Eins-zu-Eins-Entsprechung mit den Nischen stellen: das

Identitätselement entspricht , und jedes andere Gruppenelement g entspricht der Nische , die das Abbild von unter der Aktion ist von g . Diese Identifikation für ist rechts abgebildet. ${\displaystyle A_{0}}$${\displaystyle A_{0}}$${\displaystyle A=A_{0}\cdot g}$${\displaystyle A_{0}}$${\displaystyle {\widetilde{S}}_{3}}$

Beispiel: n = 2

Die affine symmetrische Gruppe wirkt auf der Linie V in der euklidischen Ebene. Die Reflexionen sind durch die gestrichelten Linien. Die Vektoren des Wurzelgitters Λ sind markiert.${\displaystyle {\widetilde{S}}_{2}}$

Algebraisch ist die

unendliche Diedergruppe , die von zwei Generatoren erzeugt wird , den Beziehungen unterworfen . Jedes andere Element der Gruppe kann als alternierendes Produkt von Kopien von und geschrieben werden . ${\displaystyle {\widetilde{S}}_{2}}$${\displaystyle s_{0},s_{1}}$${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$${\displaystyle s_{0}}$${\displaystyle s_{1}}$

Kombiniert hat die affine Permutation die Fensternotation , die der Bijektion für jede ganze Zahl

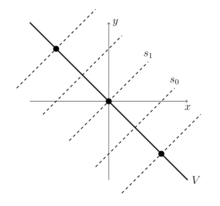
k entspricht . Die affine Permutation hat eine Fensternotation , die der Bijektion für jede ganze Zahl k entspricht . Andere Elemente haben die folgenden Fensternotationen: ${\displaystyle s_{1}}$${\displaystyle [2,1]}$${\displaystyle 2k\mapsto 2k-1,2k-1\mapsto 2k}$${\displaystyle s_{0}}$${\displaystyle [0,3]}$${\displaystyle 2k\mapsto 2k+1,2k+1\mapsto 2k}$

• ${\displaystyle \overbrace {s_{0}s_{1}\cdots s_{0}s_{1}} ^{2k\,{\text{Faktoren}}}=[1+2k,2-2k],}$
• ${\displaystyle \overbrace {s_{1}s_{0}\cdots s_{1}s_{0}} ^{2k\,{\text{Faktoren}}}=[1-2k,2+2k],}$
• ${\displaystyle \overbrace {s_{0}s_{1}\cdots s_{0}} ^{2k+1\,{\text{Faktoren}}}=[2+2k,1-2k],}$
• ${\displaystyle \overbrace {s_{1}s_{0}\cdots s_{1}} ^{2k+1\,{\text{Faktoren}}}=[2-2(k+1),1+2 (k+1)].}$

Geometrisch ist der Raum V die Gerade mit Gleichung in der Euklidischen Ebene . Das Wurzelgitter innerhalb von

V besteht aus diesen Paaren für das Integral a . Der Coxeter-Generator wirkt auf V durch Reflexion über die Linie (d. h. über den Ursprung); der Generator wirkt auf V durch Reflexion über die Linie (dh, über den Punkt ist . Es ist natürlich , um die Linie zu identifizieren V mit der durchgezogenen Linie , um den Punkt zu senden an den reellen Zahl 2 x . Mit dieser Identifizierung, die Wurzel Gitter bestehen der geraden ganzen Zahlen, die fundamentale Nische ist das Intervall [0, 1] , das Element wirkt durch Translation um k für jede ganze Zahl k und die Spiegelung spiegelt sich über den Punkt − k für jede ganze Zahl k . ${\displaystyle x+y=0}$${\displaystyle \mathbb{R} ^{2}}$${\displaystyle (a,-a)}$${\displaystyle s_{1}}$${\displaystyle x=y}$${\displaystyle s_{0}}$${\displaystyle x=y+1}$${\displaystyle \left({\tfrac {1}{2}},-{\tfrac {1}{2}}\right)}$${\displaystyle \mathbb {R} ^{1}}$${\displaystyle (x,-x)}$${\displaystyle (s_{1}s_{0})^{k}}$${\displaystyle s_{1}(s_{0}s_{1})^{k}}$

Permutationsstatistiken und Permutationsmuster

Viele Permutationsstatistiken und andere Merkmale der Kombinatorik endlicher Permutationen können auf den affinen Fall ausgedehnt werden.

Abfahrten, Länge und Inversionen

Die Länge eines Elements

g einer Coxeter-Gruppe G ist die kleinste Zahl k, so dass g als Produkt von k Coxeter-Generatoren von G geschrieben werden kann . ${\displaystyle \ell (g)}$${\displaystyle g=s_{i_{1}}\cdots s_{i_{k}}}$

Geometrisch ist die Länge eines Elements g in die Anzahl der reflektierenden Hyperebenen, die sich trennen und , wo ist die fundamentale Nische (der Simplex, der von den reflektierenden Hyperebenen der Coxeter-Generatoren begrenzt wird ). (Tatsächlich gilt das gleiche für jede affine Coxeter-Gruppe.) ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle A_{0}}$${\displaystyle A_{0}\cdot g}$${\displaystyle A_{0}}$${\displaystyle s_{0},s_{1},\ldots ,s_{n-1}}$

Kombinatorisch wird die Länge einer affinen Permutation im Sinne eines geeigneten Begriffs von Inversionen kodiert . Insbesondere hat man für eine affine Permutation u dass

$${\displaystyle \ell(u)=\#\left\{(i,j)\colon i\in\{1,\ldots,n\},i<j,{\text{ und }}u(i )>u(j)\rechts\}.}$$

Alternativ ist es die Anzahl der Äquivalenzklassen von Paaren, so dass und unter der Äquivalenzrelation if für eine ganze Zahl k . ${\displaystyle(i,j)\in\mathbb{Z}\times\mathbb{Z}}$${\displaystyle i<j}$${\displaystyle u(i)>u(j)}$${\displaystyle (i,j)\equiv (i',j')}$${\displaystyle (i-i',j-j')=(kn,kn)}$

Die erzeugende Funktion für die Länge in ist ${\displaystyle {\widetilde{S}}_{n}}$

$${\displaystyle \sum _{g\in {\widetilde{S}}_{n}}q^{\ell (g)}={\frac {1-q^{n}}{(1-q) ^{n}}}.}$$

In ähnlicher Weise kann man ein affines Analogon von Abstiegen in Permutationen definieren: Sagen Sie, dass eine affine Permutation u einen Abstieg in Position i hat, wenn . (Nach Periodizität hat

u genau dann einen Abstieg in Position i, wenn es für alle ganzen Zahlen k einen Abstieg in Position hat .) ${\displaystyle u(i)>u(i+1)}$${\displaystyle i+kn}$

Algebraisch entsprechen die Abfahrten den richtigen Abfahrten im Sinne von Coxeter-Gruppen; das heißt, i ist genau dann ein Abstieg von u, wenn . Die linken Abstiege (d. h. die Indizes

i , die die Abstiege der inversen affinen Permutation sind ; äquivalent sind sie die Werte i, so dass i vor i − 1 in der Folge auftritt . ${\displaystyle \ell (u\cdot s_{i})<\ell (u)}$${\displaystyle \ell (s_{i}\cdot u)<\ell (u)}$${\displaystyle u^{-1}}$ ${\displaystyle \ldots ,u(-2),u(-1),u(0),u(1),u(2),\ldots}$

Geometrisch ist i genau dann ein Abstieg von u, wenn die feste Hyperebene von die Nischen und trennt . ${\displaystyle s_{i}}$${\displaystyle A_{0}}$${\displaystyle A_{0}\cdot u}$

Da es für die Anzahl der Abstiege einer affinen Permutation nur endlich viele Möglichkeiten gibt, aber unendlich viele affine Permutationen, ist es nicht möglich, naiv eine erzeugende Funktion für affine Permutationen nach Anzahl der Abstiege zu bilden (ein affines Analogon der Eulerschen Polynome ). Eine mögliche Auflösung besteht darin, affine Abstiege (äquivalent zyklische Abstiege) in der endlichen symmetrischen Gruppe zu betrachten . Eine andere besteht darin, gleichzeitig die Länge und Anzahl der Abstiege einer affinen Permutation zu berücksichtigen. Die erzeugende Funktion für diese Statistik über gleichzeitig für alle

n ist ${\displaystyle S_{n}}$${\displaystyle {\widetilde{S}}_{n}}$

$${\displaystyle \sum _{n\geq 1}{\frac {x^{n}}{1-q^{n}}}\sum _{w\in {\widetilde {S}}_{n} }t^{\operatorname {des} (w)}q^{\ell (w)}=\left[{\frac {x\cdot {\frac {\partial }{\partial {x}}}\log (\exp(x;q))}{1-t\exp(x;q)}}\right]_{x\mapsto x{\frac {1-t}{1-q}}}}$$

wobei des( w ) die Anzahl der Abstiege der affinen Permutation w und die q- Exponentialfunktion ist . ${\displaystyle \exp(x;q)=\sum _{n\geq 0}{\frac {x^{n}(1-q)^{n}}{(1-q)(1-q^ {2})\cdots (1-q^{n})}}}$

Zyklustyp und Reflexionslänge

Jede Bijektion unterteilt die ganzen Zahlen in eine (möglicherweise unendliche) Liste von (möglicherweise unendlichen) Zyklen: für jede ganze Zahl

i ist der Zyklus, der i enthält, die Sequenz, in der die Exponentiation die funktionale Zusammensetzung darstellt. Zum Beispiel kann die affine Permutation in mit Fenstern Notation enthält die zwei unendlichen Zyklen und sowie unendlich viele finite Zyklen für jede . Zyklen einer affinen Permutation entsprechen offensichtlich Zyklen der zugrunde liegenden Permutation: Im obigen Beispiel mit zugrunde liegender Permutation entspricht der erste unendliche Zyklus dem Zyklus (1), der zweite dem Zyklus (45) und der endliche Zyklen entsprechen alle dem Zyklus (23). ${\displaystyle u:\mathbb{Z}\to\mathbb{Z}}$${\displaystyle (\ldots,u^{-2}(i),u^{-1}(i),i,u(i),u^{2}(i),\ldots)}$${\displaystyle {\widetilde{S}}_{5}}$${\displaystyle [6,3,2,0,4]}$${\displaystyle (\ldots,-9,-4,1,6,11,\ldots)}$${\displaystyle (\ldots,10,9,5,4,0,-1,-5\ldots)}$${\displaystyle (5k+2,5k+3)}$${\displaystyle k\in\mathbb{Z}}$${\displaystyle [1,3,2,5,4]=(1)(23)(45)}$

Für eine affine Permutation u sind folgende Bedingungen äquivalent: Alle Kreise von u sind endlich, u hat endliche Ordnung und die geometrische Wirkung von u auf den Raum V hat mindestens einen Fixpunkt.

Die Reflexionslänge eines Elements

u von ist die kleinste Zahl k, so dass es Reflexionen gibt, so dass . (In der symmetrischen Gruppe sind Reflexionen Transpositionen, und die Reflexionslänge einer Permutation ist u ist , wobei die Anzahl der Zyklen von u ist .) In ( Lewis et al. 2019 ) wurde die folgende Formel für die Reflexionslänge von an . bewiesen affine Permutation u : Definiere für jeden Zyklus von u das Gewicht als die ganze Zahl k, so dass sich aufeinanderfolgende Einträge kongruent modulo n um genau kn unterscheiden . (Zum Beispiel hat in der obigen Permutation der erste unendliche Zyklus das Gewicht 1 und der zweite unendliche Zyklus das Gewicht −1; alle endlichen Zyklen haben das Gewicht 0.) Bilden Sie ein Tupel der Zyklusgewichte von u (Zählen des gleichen Zyklus um ein Vielfaches von n nur einmal) und definieren Sie die Nichtigkeit als die Größe der kleinsten Mengenpartition dieses Tupels, sodass jeder Teil die Summe 0 ergibt. (Im obigen Beispiel ist das Tupel und die Nichtigkeit 2, da kann die Partition .) die Reflexionslänge Dann u ist ${\displaystyle \ell_{R}(u)}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle r_{1},\ldots,r_{k}}$${\displaystyle u=r_{1}\cdots r_{k}}$${\displaystyle nc(u)}$${\displaystyle c(u)}$${\displaystyle [5,2,0,3]}$ ${\displaystyle \nu (u)}$${\displaystyle (1,-1,0)}$${\displaystyle (1,-1),(0)}$

$${\displaystyle \ell_{R}(u)=n-2\nu(u)+c(\pi(u)),}$$

wo ist die zugrunde liegende Permutation von u . ${\displaystyle \pi(u)}$

Für jede affine Permutation u gibt es eine Untergruppe W von so dass , , und für die von diesem semidirekten Produkt implizierte Standardform gilt . ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle W\cong S_{n}}$${\displaystyle {\widetilde{S}}_{n}=W\ltimes \Lambda}$${\displaystyle u=w\cdot t}$${\displaystyle \ell_{R}(u)=\ell_{R}(w)+\ell_{R}(t)}$

Vollständig kommutative Elemente und Mustervermeidung

Ein reduziertes Wort für ein Element g einer Coxeter-Gruppe ist ein Tupel von Coxeter-Generatoren minimaler Länge, so dass . Das Element

g heißt voll kommutativ, wenn man jedes reduzierte Wort in jedes andere umwandeln kann, indem man kommutierende Faktorenpaare sequentiell vertauscht. In der endlichen symmetrischen Gruppe ist das Element beispielsweise voll kommutativ, da seine beiden reduzierten Wörter und durch Vertauschen von Kommutierungsfaktoren verbunden werden können, aber nicht vollständig kommutativ, weil es keine Möglichkeit gibt, das reduzierte Wort ausgehend vom reduzierten Wort um zu erreichen Kommutierungen. ${\displaystyle (s_{i_{1}},\ldots ,s_{i_{\ell (g)}})}$${\displaystyle g=s_{i_{1}}\cdots s_{i_{\ell (g)}}}$${\displaystyle S_{4}}$${\displaystyle 2143=(12)(34)}$${\displaystyle (s_{1},s_{3})}$${\displaystyle (s_{3},s_{1})}$${\displaystyle 3214=(13)(2)(4)}$${\displaystyle (s_{2},s_{1},s_{2})}$${\displaystyle (s_{1},s_{2},s_{1})}$

Billey, Jockusch & Stanley (1993) haben bewiesen, dass eine Permutation in der endlichen symmetrischen Gruppe genau dann voll kommutativ ist, wenn sie das

Permutationsmuster 321 vermeidet , d Folge. In ( Green 2002 ) wurde dieses Ergebnis auf affine Permutationen erweitert: Eine affine Permutation u ist genau dann voll kommutativ, wenn es keine ganzen Zahlen gibt, so dass . ${\displaystyle S_{n}}$${\displaystyle i<j<k}$${\displaystyle u(i)>u(j)>u(k)}$

Die Anzahl affiner Permutationen, die ein einzelnes Muster p vermeiden, ist genau dann endlich, wenn p das Muster 321 vermeidet, so dass es insbesondere unendlich viele vollständig kommutative affine Permutationen gibt. Diese wurden in ( Hanusa & Jones 2010 ) nach Länge aufgezählt .

Parabolische Untergruppen und andere Strukturen

Die parabolischen Untergruppen von und ihre Nebenklassenvertreter bieten eine reiche kombinatorische Struktur. Andere Aspekte der affinen symmetrischen Gruppe, wie ihre Bruhat-Ordnungs- und Darstellungstheorie, können auch über kombinatorische Modelle verstanden werden. ${\displaystyle {\widetilde{S}}_{n}}$

Parabolische Untergruppen, Nebengruppenrepräsentanten

Abakusdiagramm der affinen Permutation [−5, 0, 6, 9].

Eine

parabolische Standarduntergruppe einer Coxeter-Gruppe ist eine Untergruppe, die von einer Untermenge ihres Coxeter-Erzeugungssatzes erzeugt wird. Die maximalen parabolischen Untergruppen ergeben sich aus dem Weglassen eines einzelnen Coxeter-Generators. In sind alle maximalen parabolischen Untergruppen isomorph zur endlichen symmetrischen Gruppe . Die von der Teilmenge erzeugte Untergruppe besteht aus den affinen Permutationen, die das Intervall stabilisieren , dh jedes Element dieses Intervalls auf ein anderes Element des Intervalls abbilden. ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle S_{n}}$${\displaystyle \{s_{0},\ldots,s_{n-1}\}\smallsetminus \{s_{i}\}}$${\displaystyle [i+1,i+n]}$

Die nicht-maximalen parabolischen Untergruppen von sind alle isomorph zu parabolischen Untergruppen von , dh zu einer Young-Untergruppe für einige positive ganze Zahlen mit der Summe n . ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle S_{n}}$ ${\displaystyle S_{a_{1}}\times \cdots \times S_{a_{k}}}$${\displaystyle a_{1},\ldots ,a_{k}}$

Für ein festes Element i von sei die maximale echte Teilmenge von Coxeter-Generatoren unter Weglassung , und bezeichne die von J erzeugte parabolische Untergruppe . Jede Nebenklasse hat ein eindeutiges Element minimaler Länge. Die Sammlung solcher Repräsentanten, bezeichnet mit , besteht aus den folgenden affinen Permutationen: ${\displaystyle \{0,\ldots,n-1\}}$${\displaystyle J=\{s_{0},\ldots,s_{n-1}\}\smallsetminus \{s_{i}\}}$${\displaystyle s_{i}}$${\displaystyle ({\widetilde{S}}_{n})_{J}}$ ${\displaystyle g\cdot ({\widetilde{S}}_{n})_{J}}$${\displaystyle ({\widetilde{S}}_{n})^{J}}$

In dem besonderen Fall, dass , also die Standardkopie von inside ist , können die Elemente von natürlich durch Abakusdiagramme dargestellt werden : die ganzen Zahlen sind in einem unendlichen Streifen der Breite n angeordnet , der sequentiell entlang der Reihen und dann von oben nach unten ansteigt; ganze Zahlen sind eingekreist, wenn sie direkt über einem der Fenstereinträge des minimalen Nebenklassenrepräsentanten liegen. Der Repräsentant der minimalen Nebenklassen wird beispielsweise durch das Abakus-Diagramm rechts dargestellt. Um die Länge des Repräsentanten aus dem Abakus-Diagramm zu berechnen, addiert man die Anzahl der nicht eingekreisten Zahlen, die kleiner sind als der letzte eingekreiste Eintrag in jeder Spalte. (Im gezeigten Beispiel ergibt dies .) ${\displaystyle J=\{s_{1},\ldots ,s_{n-1}\}}$${\displaystyle ({\widetilde{S}}_{n})_{J}\cong S_{n}}$${\displaystyle S_{n}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle ({\widetilde{S}}_{n})^{J}\cong {\widetilde{S}}_{n}/S_{n}}$${\displaystyle u=[-5,0,6,9]}$${\displaystyle 5+3+0+1=9}$

Andere kombinatorische Modelle von minimaler Länge Restklassenvertretern für die in Bezug auf den angegeben werden kann Kern Partitionen ( integer Partitionen , in denen keine Hakenlänge durch teilbar n ) oder Trennwände begrenzt (integer Partitionen , in denen kein Teil ist größer als n - 1 ). Unter diesen Entsprechungen kann gezeigt werden, dass die schwache Bruhat-Ordnung auf einer bestimmten Teilmenge des Youngschen Gitters isomorph ist . ${\displaystyle {\widetilde {S}}_{n}/S_{n}}$${\displaystyle {\widetilde {S}}_{n}/S_{n}}$

Bruhat-Auftrag

Die Bruhat Reihenfolge auf die folgende kombinatorische Umsetzung. Wenn u eine affine Permutation ist und i und j ganze Zahlen sind, definieren Sie die Anzahl der ganzen Zahlen a, so dass und . (Zum Beispiel mit , hat man : die drei relevanten Werte sind , die durch jeweils zugeordnet ist u auf 1, 2 und 4) , dann zwei affine Permutationen u , v , hat man , dass in Bruhat Reihenfolge , wenn und nur wenn für alle ganzen Zahlen i , j . ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle u[i,j]}$${\displaystyle a\leq i}$${\displaystyle u(a)\geq j}$${\displaystyle u=[2,0,4]\in {\widetilde{S}}_{3}}$${\displaystyle u[3,1]=3}$${\displaystyle a=0,1,3}$${\displaystyle u\leq v}$${\displaystyle u[i,j]\leq v[i,j]}$

Darstellungstheorie und eine affine Robinson-Schensted-Korrespondenz

In der endlichen symmetrischen Gruppe ergibt die Robinson-Schensted-Korrespondenz eine Bijektion zwischen der Gruppe und Paaren von Standard-Young-Tableaus derselben Form. Diese Bijektion spielt eine zentrale Rolle in der Kombinatorik und der Darstellungstheorie der symmetrischen Gruppe . Zum Beispiel liegen in der Sprache der Kazhdan-Lusztig-Theorie zwei Permutationen genau dann in derselben linken Zelle, wenn ihre Bilder unter Robinson-Schensted dasselbe Tableau Q aufweisen , und in derselben rechten Zelle genau dann, wenn ihre Bilder die gleiches Bild P . In ( Shi 1986 ), J.-Y. Shi zeigte, dass linke Zellen für stattdessen durch Boulevardblätter indiziert werden , und gab in ( Shi 1991 ) einen Algorithmus zur Berechnung des Boulevardblatts analog zum Tableau P für eine affine Permutation. In ( Chmutov, Pylyavskyy & Yudovina 2018 ) erweiterten die Autoren Shis Arbeit um eine bijektive Karte zwischen und Tripeln, bestehend aus zwei Boulevardblättern gleicher Form und einem ganzzahligen Vektor, deren Einträge bestimmte Ungleichungen erfüllen. Ihr Verfahren verwendet die Matrixdarstellung affiner Permutationen und verallgemeinert die Schattenkonstruktion von Viennot (1977) . ${\displaystyle (P,Q)}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle (P,Q,\rho)}$

Inverse Realisierungen

In manchen Situationen möchte man vielleicht die Wirkung der affinen symmetrischen Gruppe auf oder auf Alkoven betrachten, die zu der oben angegebenen invers ist. Wir beschreiben diese alternativen Realisierungen jetzt. ${\displaystyle \mathbb{Z}}$

Bei der kombinatorischen Wirkung von on wirkt der Generator durch Umschalten der Werte i und i +1 . Umgekehrt vertauscht es stattdessen die Einträge in den Positionen i und i + 1 . In ähnlicher Weise besteht die Aktion einer allgemeinen Reflexion darin, die Einträge an den Positionen j − kn und i + kn für jedes k zu vertauschen, wobei alle Eingaben an Positionen fixiert werden, die nicht mit i oder j modulo n kongruent sind . (In der endlichen symmetrischen Gruppe wird analog zwischen der aktiven und der passiven Form einer Permutation unterschieden.) ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle \mathbb{Z}}$${\displaystyle s_{i}}$ ${\displaystyle S_{n}}$

Bei der geometrischen Wirkung von wirkt der Generator auf eine Nische A, indem er sie über eine der Begrenzungsebenen der fundamentalen Nische A ₀ reflektiert . In der umgekehrten Aktion reflektiert es stattdessen A über eine seiner eigenen Begrenzungsebenen. Aus dieser Perspektive entspricht ein reduziertes Wort einem Alkovengang auf dem tessellierten Raum V . ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle s_{i}}$

Beziehung zu anderen mathematischen Objekten

Die affine symmetrische Gruppe ist eng mit einer Vielzahl anderer mathematischer Objekte verwandt.

Jongliermuster

In ( Ehrenborg & Readdy 1996 ) wird eine Entsprechung zwischen affinen Permutationen und Jongliermustern gegeben , die in einer Version der Siteswap - Notation kodiert sind . Hier ist ein Jongliermuster der Periode n eine Folge von nichtnegativen ganzen Zahlen (mit gewissen Einschränkungen), die das Verhalten von Bällen erfasst, die von einem Jongleur geworfen werden, wobei die Zahl die Zeit angibt, die der i- te Wurf in der Luft verbringt (entsprechend der Wurfhöhe). Die Anzahl b der Kugeln im Muster ist der Durchschnitt . Die Ehrenborg-Readdy-Korrespondenz ordnet jedem Jongliermuster der Periode n die durch definierte Funktion zu${\displaystyle (a_{1},\ldots,a_{n})}$${\displaystyle a_{i}}$${\displaystyle b={\frac {a_{1}+\ldots +a_{n}}{n}}}$${\displaystyle {\bf {a}}=(a_{1},\ldots,a_{n})}$${\displaystyle w_{\bf{a}}\colon \mathbb{Z}\to\mathbb{Z}}$

wobei Indizes der Folge a modulo n genommen werden . Dann ist eine affine Permutation in , und außerdem entsteht auf diese Weise jede affine Permutation aus einem Jongliermuster. Unter dieser Bijektion wird die Länge der affinen Permutation durch eine natürliche Statistik im Jongliermuster kodiert: man hat ${\displaystyle w_{\bf {a}}}$${\displaystyle {\widetilde{S}}_{n}}$ wobei die Anzahl der Kreuzungen (bis zur Periodizität) im Bogendiagramm von a ist . Dies erlaubt einen elementaren Beweis der erzeugenden Funktion für affine Permutationen nach Länge. ${\displaystyle \operatorname {cross} ({\bf {a}})}$

Zum Beispiel hat das Jongliermuster 441 (rechts dargestellt) und . Daher entspricht es der affinen Permutation . Das Jongliermuster hat vier Kreuzungen und die affine Permutation hat die Länge . ${\displaystyle n=3}$${\displaystyle b={\frac {4+4+1}{3}}=3}$${\displaystyle w_{441}=[1+4-3,2+4-3,3+1-3]=[2,3,1]}$${\displaystyle \ell(w_{441})=(3-1)\cdot 3-4=2}$

Ähnliche Techniken können verwendet werden, um die Erzeugungsfunktion für Repräsentanten minimaler Nebenklassen der Länge abzuleiten . ${\displaystyle {\widetilde {S}}_{n}/S_{n}}$

Komplexe Reflexionsgruppen

In einem endlichdimensionalen reellen inneren Produktraum ist eine Spiegelung eine lineare Transformation , die eine lineare Hyperebene punktweise fixiert und den Vektor orthogonal zur Ebene negiert. Dieser Begriff kann auf Vektorräume über andere Felder erweitert werden . Insbesondere in einem komplexen inneren Produktraum ist eine Spiegelung eine unitäre Transformation T endlicher Ordnung, die eine Hyperebene fixiert. Dies impliziert, dass die Vektoren orthogonal zur Hyperebene Eigenvektoren von T sind und der zugehörige Eigenwert eine komplexe Einheitswurzel ist . Eine komplexe Reflexionsgruppe ist eine endliche Gruppe von linearen Transformationen in einem komplexen Vektorraum, die durch Reflexionen erzeugt werden.

Die komplexen Reflexionsgruppen wurden von Shephard & Todd (1954) vollständig klassifiziert : jede komplexe Reflexionsgruppe ist isomorph zu einem Produkt irreduzibler komplexer Reflexionsgruppen, und jede irreduzible gehört entweder zu einer unendlichen Familie (wobei

m , p und n positive ganze Zahlen sind so dass p m teilt ) oder ist eines von 34 anderen (sogenannten "außergewöhnlichen") Beispielen. Die Gruppe ist die verallgemeinerte symmetrische Gruppe : algebraisch ist sie das Kranzprodukt der zyklischen Gruppe mit der symmetrischen Gruppe . Konkret können die Elemente der Gruppe durch monomische Matrizen (Matrizen mit einem Eintrag ungleich Null in jeder Zeile und Spalte) dargestellt werden, deren Einträge ungleich Null alle m- te Einheitswurzeln sind. Die Gruppen sind Untergruppen von , und insbesondere besteht die Gruppe aus den Matrizen, in denen das Produkt der von Null verschiedenen Einträge gleich 1 ist. ${\displaystyle G(m,p,n)}$${\displaystyle G(m,1,n)}$ ${\displaystyle (\mathbb{Z} /m\mathbb{Z})\wr S_{n}}$ ${\displaystyle \mathbb{Z} /m\mathbb{Z}}$${\displaystyle S_{n}}$${\displaystyle G(m,p,n)}$${\displaystyle G(m,1,n)}$${\displaystyle G(m,m,n)}$

In ( Shi 2002 ) zeigte Shi, dass die affine symmetrische Gruppe eine generische Abdeckung der Familie ist , im folgenden Sinne: für jede positive ganze Zahl

m gibt es eine Surjektion von bis , und diese Abbildungen sind mit den natürlichen Surjektionen kompatibel, wenn das kommen aus der Erhöhung jedes Eintrags in die m / p- te Potenz. Darüber hinaus respektieren diese Projektionen die Reflexionsgruppenstruktur, indem das Bild jeder Reflexion in darunter eine Reflexion in ist ; und ähnlich, wenn das Bild des Standard- Coxeter-Elements in ein Coxeter-Element in ist . ${\displaystyle \left\{G(m,m,n)\colon m\geq 1\right\}}$${\displaystyle \pi_{m}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle G(m,m,n)}$${\displaystyle G(m,m,n)\twoheadrightarrow G(p,p,n)}$${\displaystyle p\mid m}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle \pi_{m}}$${\displaystyle G(m,m,n)}$${\displaystyle m>1}$ ${\displaystyle s_{0}\cdot s_{1}\cdots s_{n-1}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle G(m,m,n)}$

Affine Lie-Algebren

Jede affine Coxeter-Gruppe ist einer affinen Lie-Algebra zugeordnet , einer bestimmten unendlichdimensionalen nicht-assoziativen Algebra mit ungewöhnlich schönen darstellungstheoretischen Eigenschaften. In dieser Assoziation entsteht die Coxeter-Gruppe als eine Gruppe von Symmetrien des Wurzelraums der Lie-Algebra (dem Dual der Cartan-Subalgebra). In der Klassifikation affiner Lie-Algebren ist diejenige, die mit assoziiert ist, vom (unverdrillten) Typ , mit

Cartan-Matrix für und ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle A_{n-1}^{(1)}}$ ${\displaystyle {\begin{bmatrix}2&-2\\-2&2\end{bmatrix}}}$${\displaystyle n=2}$

$${\displaystyle {\begin{bmatrix}2&-1&0&\cdots &0&-1\\-1&2&-1&\cdots &0&0\\0&-1&2&\cdots &0&0\\\vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&0&\cdots &2&-1\\-1&0&0&\cdots &-1&2\end{bmatrix}}}$$

(eine zirkulierende Matrix ) für . ${\displaystyle n>2}$

Wie andere Kac-Moody-Algebren erfüllen affine Lie-Algebren die Weyl-Kac-Zeichenformel , die die Zeichen der Algebra in Bezug auf ihre höchsten Gewichte ausdrückt . Bei affinen Lie-Algebren sind die resultierenden Identitäten äquivalent zu den Macdonald-Identitäten . Insbesondere für die affine Lie - Algebra vom Typ , die der affinen symmetrischen Gruppe zugeordnet ist , ist die entsprechende Macdonald - Identität äquivalent zum

Jacobi - Tripelprodukt . ${\displaystyle A_{1}^{(1)}}$${\displaystyle {\widetilde{S}}_{2}}$

Erweiterte affine symmetrische Gruppe

Die affine symmetrische Gruppe ist eine Untergruppe der erweiterten affinen symmetrischen Gruppe . Die erweiterte Gruppe ist isomorph zum Kranzprodukt . Seine Elemente sind

erweiterte affine Permutationen : Bijektionen derart, dass für alle ganzen Zahlen x . Anders als die affine symmetrische Gruppe ist die erweiterte affine symmetrische Gruppe keine Coxeter-Gruppe. Es hat jedoch einen natürlichen Generierungssatz, der den Coxeter-Erzeugungssatz um erweitert : Der Verschiebungsoperator, dessen Fensternotation ist, erzeugt die erweiterte Gruppe mit den einfachen Reflexionen, vorbehaltlich der zusätzlichen Beziehungen . ${\displaystyle \mathbb{Z} \wr S_{n}}$${\displaystyle u\colon\mathbb{Z}\to\mathbb{Z}}$${\displaystyle u(x+n)=u(x)+n}$${\displaystyle {\widetilde{S}}_{n}}$ ${\displaystyle \tau}$${\displaystyle \tau =[2,3,\ldots ,n,n+1]}$${\displaystyle \tau s_{i}\tau^{-1}=s_{i+1}}$

Kombinatorik anderer affiner Coxeter-Gruppen

Die geometrische Wirkung der affinen symmetrischen Gruppe ordnet sie natürlich in die Familie der

affinen Coxeter-Gruppen ein , die alle eine ähnliche geometrische Wirkung haben. Die kombinatorische Beschreibung der kann auch auf viele dieser Gruppen ausgedehnt werden: In Eriksson & Eriksson (1998) wird eine axiomatische Beschreibung bestimmter Permutationsgruppen gegeben, auf die einwirkt (die "George-Gruppen", zu Ehren von George Lusztig ) und es wird gezeigt, dass es sich genau um die "klassischen" Coxeter-Gruppen der endlichen und affinen Typen A, B, C und D handelt. Die kombinatorischen Interpretationen von Descents, Inversionen usw. übertragen sich also in diesen Fällen. Abakusmodelle von Nebenklassenrepräsentanten minimaler Länge für parabolische Quotienten wurden ebenfalls auf diesen Kontext erweitert. ${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle {\widetilde{S}}_{n}}$${\displaystyle \mathbb{Z}}$

Anmerkungen

Dieser Artikel wurde von der folgenden Quelle unter einer CC BY 4.0- Lizenz ( 2021 ) angepasst ( Rezensentenberichte ): Joel Brewster Lewis (21. April 2021). "Affine symmetrische Gruppe" (PDF) . WikiJournal of Science . 4 (1): 3. doi : 10.15347/WJS/2021.003 . ISSN  2470-6345 . Wikidata  Q100400684 .

Verweise

• Beazley, Elizabeth; Nichols, Margaret; Park, Min-Hae; Shi, XiaoLin; Youcis, Alexander (2015), "Bijektive Projektionen auf parabolische Quotienten affiner Weylgruppen", J. Algebr. Kamm. , 41 (4): 911–948, doi : 10.1007/s10801-014-0559-9
• Berg, Chris; Jones, Brant; Vazirani, Monica (2009), "Eine Bijektion auf Kernpartitionen und ein parabolischer Quotient der affinen symmetrischen Gruppe", J. Combin. Theorie Ser. A , 116 (8): 1344–1360, arXiv : 0804.1380 , doi : 10.1016/j.jcta.2009.03.013 , S2CID  3032099
• Billey, Sara C .; Jockusch, William; Stanley, Richard P. (1993), "Einige kombinatorische Eigenschaften von Schubert-Polynomen", J. Algebr. Kamm. , 2 (4): 345–374, doi : 10.1023/A:1022419800503
• Björner, Anders ; Brenti, Francesco (1996), "Affine Permutationen des Typs A", Electron. J. Kombinieren. , 3 (2): R18, doi : 10.37236/1276
• Björner, Anders ; Brenti, Francesco (2005), Kombinatorik von Coxeter-Gruppen , Springer, ISBN 978-3540-442387
• Cameron, Peter J. (1994), Kombinatorik: Themen, Techniken, Algorithmen , Cambridge University Press, ISBN 978-0-521-45761-3
• Chmutov, Michael; Pyljavskyj, Pawlo; Yudovina, Elena (2018), "Matrix-Kugel-Konstruktion affiner Robinson-Schensted-Korrespondenz", Selecta Math. , Neue Serie, 24 (2): 667–750, arXiv : 1511.05861 , doi : 10.1007/s00029-018-0402-6 , S2CID  119086049
• Clark, Eric; Ehrenborg, Richard (2011), "Excedances of affin permutations", Advances in Applied Mathematics , 46 (1–4): 175–191, doi : 10.1016/j.aam.2009.12.06
• Crites, Andrew (2010), „Mustervermeidung für affine Permutationen aufzählen“, Electron. J. Kombinieren. , 17 (1): R127, arXiv : 1002,1933 , doi : 10,37236/399
• Ehrenborg, Richard ; Readdy, Margaret (1996), "Juggling und Anwendungen auf q -Analoga", Discrete Math. , 157 (1–3): 107–125, CiteSeerX  10.1.1.8.6684 , doi : 10.1016/S0012-365X(96)83010-X
• Eriksson, Henrik; Eriksson, Kimmo (1998), "Affine Weyl-Gruppen als unendliche Permutationen", Electron. J. Kombinieren. , 5 : R18, doi : 10.37236/1356
• Green, RM (2002), "Über 321-Vermeidung von Permutationen in affinen Weyl-Gruppen", J. Algebr. Kamm. , 15 (3): 241–252, doi : 10.1023/A:1015012524524
• Hanusa, Christopher RH; Jones, Brant C. (2010), „Die Aufzählung von vollständig kommutativen affinen Permutationen“, Eur. J. Kamm. , 31 (5): 1342–1359, arXiv : 0907.0709 , doi : 10.1016/j.ejc.2009.11.010 , S2CID  789357
• Hanusa, Christopher RH; Jones, Brant C. (2012), „Abacus models for parabolic quotients of affin Weyl groups“, J. Algebra , 361 : 134–162, doi : 10.1016/j.jalgebra.2012.03.029
• Humphreys, James E. (1990), Reflexionsgruppen und Coxeter-Gruppen , Cambridge University Press, ISBN 0-521-37510-X
• Kac, Victor G. (1990), Unendlichdimensionale Lie-Algebren (3. Aufl.), Cambridge University Press, ISBN 0-521-46693-8
• Knutson, Allen ; Lam, Thomas; Speyer, David E. (2013), "Positroid-Varietäten: Jonglieren und Geometrie", Compos. Mathematik. , 149 (10): 1710–1752, doi : 10.1112/S0010437X13007240
• Lam, Thomas (2015), "Die Form eines zufälligen affinen Weyl-Gruppenelements und zufällige Kernpartitionen", Ann. Wahrscheinlich. , 43 (4): 1643–1662, doi : 10.1214/14-AOP915
• Lapointe, Luc; Morse, Jennifer (2005), "Tableaux auf -Kernen, reduzierte Wörter für affine Permutationen und -Schur-Erweiterungen",

J. Combin. Theorie Ser. A , 112 (1): 44–81, doi : 10.1016/j.jcta.2005.01.003 , S2CID 161241${\displaystyle k+1}$${\displaystyle k}$ 

Lewis, Joel Brewster (2020), "Eine Anmerkung zur Hurwitz-Aktion zur Reflexionsfaktorisierung von Coxeter-Elementen in komplexen Reflexionsgruppen", Electron. J. Kombinieren. , 27 (2): P2.54, arXiv : 2001.08238 , doi : 10.37236/9351

Lewis, Joel Brewster; McCammond, Jon; Petersen, T. Kyle; Schwer, Petra (2019), "Berechnung der Reflexionslänge in einer affinen Coxeter-Gruppe", Übers. Amer. Mathematik. Soz. , 371 (6): 4097–4127, doi : 10.1090/tran/7472

Petersen, T. Kyle (2015), Eulersche Zahlen , Birkhäuser Advanced Texts Basler Lehrbücher, Birkhauser, doi : 10.1007/978-1-4939-3091-3 , ISBN 978-1-4939-3090-6

Polster, Burkard (2003), Die Mathematik des Jonglierens , Springer, ISBN 0-387-95513-5

Reiner, Victor (1995), "Die Verteilung von Abstiegen und Länge in einer Coxeter-Gruppe", Electron. J. Kombinieren. , 2 : R25, doi : 10.37236/1219

Schäfer, GC ; Todd, JA (1954), "Finite unitary Reflection groups", Canad. J.Math. , 6 : 274–304, doi : 10.4153/CJM-1954-028-3

Shi, Jian-Yi (1986), Kazhdan-Lusztig-Zellen bestimmter affiner Weyl-Gruppen , Lecture Notes in Mathematics, 1179 , Springer, ISBN 3-540-16439-1

Shi, Jian-Yi (1991), "The generalized Robinson-Schensted algorithm on the affin Weyl group of type A _{n −1} ", J. Algebra , 139 (2): 364–394, CiteSeerX  10.1.1.551.3094 , doi : 10.1016/0021-8693(91)90300-W

Shi, Jian-Yi (2002), "Bestimmte imprimitive Reflexionsgruppen und ihre generischen Versionen", Trans. Amer. Mathematik. Soz. , 354 (5): 2115–2129, doi : 10.1090/S0002-9947-02-02941-0

Stembridge, John (1996), "Über die vollständig kommutativen Elemente von Coxeter-Gruppen", J. Algebr. Kamm. , 5 (4): 353–385, doi : 10.1007/BF00193185

Viennot, G. (1977), "Une forme géométrique de la Correspondance de Robinson-Schensted", in Foata, Dominique (Hrsg.), Combinatoire et représentation du groupe symétrique , Lecture Notes in Mathematics, 579 , Springer, S. 29– 58, doi : 10.1007/BFb0090011 , ISBN 978-3-540-08143-2