Blockcode - Block code

In der Codierungstheorie sind Blockcodes eine große und wichtige Familie von Fehlerkorrekturcodes , die Daten in Blöcken codieren. Es gibt eine Vielzahl von Beispielen für Blockcodes, von denen viele eine breite Palette praktischer Anwendungen haben. Die abstrakte Definition von Blockcodes ist konzeptionell nützlich, da Codierungstheoretiker, Mathematiker und Informatiker die Einschränkungen aller Blockcodes auf einheitliche Weise untersuchen können. Solche Einschränkungen treten häufig in Form von Grenzen auf , die unterschiedliche Parameter des Blockcodes miteinander in Beziehung setzen, wie z. B. seine Rate und seine Fähigkeit, Fehler zu erkennen und zu korrigieren.

Beispiele für Blockcodes sind Reed-Solomon-Codes , Hamming-Codes , Hadamard-Codes , Expander-Codes , Golay-Codes und Reed-Muller-Codes . Diese Beispiele gehören auch zur Klasse der linearen Codes und werden daher als lineare Blockcodes bezeichnet . Insbesondere sind diese Codes als algebraische Blockcodes oder zyklische Blockcodes bekannt, da sie unter Verwendung von Booleschen Polynomen erzeugt werden können.

Algebraische Blockcodes sind in der Regel hart dekodierten algebraische Decodierer verwendet wird .

Der Begriff Blockcode kann sich auch auf jeden Fehlerkorrekturcode beziehen, der auf einen Block von Eingangsdatenbits einwirkt , um Ausgangsdatenbits zu erzeugen . Folglich ist der Blockcodierer eine speicherlose Vorrichtung. Unter dieser Definition würden Codes wie Turbocodes , terminierte Faltungscodes und andere iterativ decodierbare Codes (turboähnliche Codes) ebenfalls als Blockcodes betrachtet. Ein nicht-terminiertes Faltungscodierer wäre ein Beispiel für einen nicht-Block (ungerahmt) Code sein, welchen Speicher und wird stattdessen als ein klassifizierte Baumcode . ${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle (n, k)}$

Dieser Artikel befasst sich mit "algebraischen Blockcodes".

Der Blockcode und seine Parameter

Fehlerkorrekturcodes werden verwendet , zuverlässig übertragen digitale Daten über unzuverlässige Kommunikationskanäle unterliegen Rauschkanal . Wenn ein Absender einen möglicherweise sehr langen Datenstrom unter Verwendung eines Blockcodes übertragen möchte, zerlegt der Absender den Strom in Teile fester Größe. Jedes solches Stück wird als Nachricht , und das Verfahren durch den Blockcode codiert gegeben jede Nachricht einzeln in ein Codewort, auch genannt Block im Rahmen des Blockcodes. Der Absender sendet dann alle Blöcke an den Empfänger, der seinerseits einen Decodierungsmechanismus verwenden kann, um (hoffentlich) die ursprünglichen Nachrichten aus den möglicherweise beschädigten empfangenen Blöcken wiederherzustellen. Die Leistung und der Erfolg der Gesamtübertragung hängen von den Parametern des Kanals und dem Blockcode ab.

Formal ist ein Blockcode eine injektive Zuordnung

${\ displaystyle C: \ Sigma ^ {k} \ to \ Sigma ^ {n}}$ .

Hier ist eine endliche und nicht leere Menge und und sind ganze Zahlen. Die Bedeutung und Bedeutung dieser drei Parameter und anderer Parameter im Zusammenhang mit dem Code werden nachstehend beschrieben. ${\ displaystyle \ Sigma}$${\ displaystyle k}$${\ displaystyle n}$

Das Alphabet Σ

Der zu codierende Datenstrom wird als Zeichenfolge über einem Alphabet modelliert . Die Größe des Alphabets wird oft als geschrieben . Wenn ja , wird der Blockcode als binärer Blockcode bezeichnet. In vielen Anwendungen ist es nützlich, eine Primzahl zu betrachten und sich mit dem endlichen Feld zu identifizieren . ${\ displaystyle \ Sigma}$${\ displaystyle | \ Sigma |}$${\ displaystyle q}$${\ displaystyle q = 2}$${\ displaystyle q}$${\ displaystyle \ Sigma}$ ${\ displaystyle \ mathbb {F} _ {q}}$

Die Nachrichtenlänge k

Meldungen sind Elemente der , dass, Strings der Länge ist . Daher wird die Nummer als Nachrichtenlänge oder -dimension eines Blockcodes bezeichnet. ${\ displaystyle m}$${\ displaystyle \ Sigma ^ {k}}$${\ displaystyle k}$${\ displaystyle k}$

Die Blocklänge n

Die Blocklänge eines Blockcodes ist die Anzahl der Symbole in einem Block. Daher sind die Elemente von Zeichenfolgen mit einer Länge und entsprechen Blöcken, die vom Empfänger empfangen werden können. Daher werden sie auch empfangene Wörter genannt. Wenn für eine Nachricht , dann heißt das Codewort von . ${\ displaystyle n}$${\ displaystyle c}$${\ displaystyle \ Sigma ^ {n}}$${\ displaystyle n}$${\ displaystyle c = C (m)}$${\ displaystyle m}$${\ displaystyle c}$${\ displaystyle m}$

Die Rate R.

Die Rate eines Blockcodes ist definiert als das Verhältnis zwischen seiner Nachrichtenlänge und seiner Blocklänge:

${\ displaystyle R = k / n}$ .

Eine große Rate bedeutet, dass die Menge der tatsächlichen Nachricht pro übertragenem Block hoch ist. In diesem Sinne misst die Rate die Übertragungsgeschwindigkeit und die Menge den Overhead, der aufgrund der Codierung mit dem Blockcode auftritt. Es ist eine einfache informationstheoretische Tatsache, dass die Rate nicht überschritten werden kann, da Daten im Allgemeinen nicht verlustfrei komprimiert werden können. Formal folgt dies aus der Tatsache, dass der Code eine injektive Karte ist. ${\ displaystyle 1-R}$${\ displaystyle 1}$${\ displaystyle C}$

Die Entfernung d

Der Abstand oder Mindestabstand d eines Blockcodes ist die Mindestanzahl von Positionen, an denen sich zwei unterschiedliche Codewörter unterscheiden, und der relative Abstand ist der Bruchteil . Formell bezeichnen wir für empfangene Wörter den Hamming-Abstand zwischen und , dh die Anzahl der Positionen, in denen und sich unterscheiden. Dann wird der Mindestabstand des Codes definiert als ${\ displaystyle \ delta}$${\ displaystyle d / n}$${\ displaystyle c_ {1}, c_ {2} \ in \ Sigma ^ {n}}$${\ displaystyle \ Delta (c_ {1}, c_ {2})}$${\ displaystyle c_ {1}}$${\ displaystyle c_ {2}}$${\ displaystyle c_ {1}}$${\ displaystyle c_ {2}}$${\ displaystyle d}$${\ displaystyle C}$

${\ displaystyle d: = \ min _ {m_ {1}, m_ {2} \ in \ Sigma ^ {k} \ auf m_ {1} \ neq m_ {2}} \ Delta [C (m_ {1}) , C (m_ {2})]}$ .

Da jeder Code injektiv sein muss , stimmen zwei beliebige Codewörter an mindestens einer Position nicht überein, sodass der Abstand eines Codes mindestens beträgt . Außerdem entspricht der Abstand dem Mindestgewicht für lineare Blockcodes, weil: ${\ displaystyle 1}$

${\ displaystyle \ min _ {m_ {1}, m_ {2} \ in \ Sigma ^ {k} \ auf m_ {1} \ neq m_ {2}} \ Delta [C (m_ {1}), C ( m_ {2})] = \ min _ {m_ {1}, m_ {2} \ in \ Sigma ^ {k} \ auf m_ {1} \ neq m_ {2}} \ Delta [\ mathbf {0}, C (m_ {1}) + C (m_ {2})] = \ min _ {m \ in \ Sigma ^ {k} \ auf m \ neq \ mathbf {0}} w [C (m)] = w_ {\Mindest }}$ .

Ein größerer Abstand ermöglicht eine bessere Fehlerkorrektur und -erkennung. Wenn wir beispielsweise nur Fehler berücksichtigen, die Symbole des gesendeten Codeworts ändern, diese jedoch niemals löschen oder hinzufügen, ist die Anzahl der Fehler die Anzahl der Positionen, an denen sich das gesendete Codewort und das empfangene Wort unterscheiden. Ein Code mit dem Abstand d ermöglicht es dem Empfänger, bis zu Übertragungsfehler zu erkennen, da das Ändern der Position eines Codeworts niemals versehentlich ein anderes Codewort ergeben kann. Wenn nicht mehr als Übertragungsfehler auftreten, kann der Empfänger das empfangene Wort eindeutig in ein Codewort decodieren. Dies liegt daran, dass jedes empfangene Wort höchstens ein Codewort in der Entfernung hat . Wenn mehr als Übertragungsfehler auftreten, kann der Empfänger das empfangene Wort im Allgemeinen nicht eindeutig dekodieren, da möglicherweise mehrere mögliche Codewörter vorhanden sind. Eine Möglichkeit für den Empfänger, mit dieser Situation umzugehen , besteht in der Verwendung der Listendecodierung , bei der der Decodierer eine Liste aller Codewörter in einem bestimmten Radius ausgibt. ${\ displaystyle d-1}$${\ displaystyle d-1}$${\ displaystyle (d-1) / 2}$${\ displaystyle (d-1) / 2}$${\ displaystyle (d-1) / 2}$

Beliebte Notation

Die Notation beschreibt einen Blockcode über ein Alphabet der Größe , mit einer Blocklänge , die Nachrichtenlänge , und die Entfernung . Wenn der Blockcode ein linearer Blockcode ist, werden die eckigen Klammern in der Notation verwendet, um diese Tatsache darzustellen. Bei Binärcodes mit wird der Index manchmal gelöscht. Für Codes mit maximaler Entfernung ist die Entfernung immer , aber manchmal ist die genaue Entfernung nicht bekannt, nicht trivial zu beweisen oder anzugeben oder nicht erforderlich. In solchen Fällen fehlt möglicherweise die Komponente. ${\ displaystyle (n, k, d) _ {q}}$${\ displaystyle \ Sigma}$${\ displaystyle q}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle d}$${\ displaystyle [n, k, d] _ {q}}$${\ displaystyle q = 2}$${\ displaystyle d = n-k + 1}$${\ displaystyle d}$

Manchmal, insbesondere für Nicht-Block-Codes, wird die Notation für Codes verwendet, die Codewörter mit einer Länge enthalten . Für Blockcodes mit Nachrichten mit einer Länge über einem Alphabet der Größe wäre diese Nummer . ${\ displaystyle (n, M, d) _ {q}}$${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle q}$${\ displaystyle M = q ^ {k}}$

Beispiele

Wie oben erwähnt, gibt es eine große Anzahl von Fehlerkorrekturcodes, die tatsächlich Blockcodes sind. Der erste fehlerkorrigierende Code war der Hamming (7,4) -Code, der 1950 von Richard W. Hamming entwickelt wurde. Dieser Code wandelt eine aus 4 Bits bestehende Nachricht durch Hinzufügen von 3 Paritätsbits in ein Codewort mit 7 Bits um. Daher ist dieser Code ein Blockcode. Es stellt sich heraus, dass es sich auch um einen linearen Code handelt und dass es Abstand 3 hat. In der obigen Kurzschreibweise bedeutet dies, dass der Hamming (7,4) -Code ein Code ist. ${\ displaystyle [7,4,3] _ {2}}$

Reed-Solomon-Codes sind eine Familie von Codes mit und als Hauptmacht . Rangcodes sind eine Familie von Codes mit . Hadamard-Codes sind eine Familie von Codes mit und . ${\ displaystyle [n, k, d] _ {q}}$${\ displaystyle d = n-k + 1}$${\ displaystyle q}$${\ displaystyle [n, k, d] _ {q}}$${\ displaystyle d \ leq n-k + 1}$${\ displaystyle [n, k, d] _ {2}}$${\ displaystyle n = 2 ^ {k-1}}$${\ displaystyle d = 2 ^ {k-2}}$

Eigenschaften zur Fehlererkennung und -korrektur

Ein Codewort kann als Punkt im Dimensionsraum betrachtet werden, und der Code ist die Teilmenge von . Ein Code hat Abstand bedeutet , dass , da kein anderes Codewort ist in dem Hamming Ball bei zentrierte mit Radius , die als Sammlung von definierten -Dimension Worten , deren Hamming - Abstand zu nicht mehr als . Ebenso hat mit (minimalem) Abstand die folgenden Eigenschaften: ${\ displaystyle c \ in \ Sigma ^ {n}}$${\ displaystyle n}$${\ displaystyle \ Sigma ^ {n}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle \ Sigma ^ {n}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle d}$${\ displaystyle \ forall c \ in {\ mathcal {C}}}$${\ displaystyle c}$${\ displaystyle d-1}$${\ displaystyle n}$${\ displaystyle c}$${\ displaystyle d-1}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle d}$

• ${\ displaystyle {\ mathcal {C}}}$ kann Fehler erkennen : Da ein Codewort das einzige Codewort in der Hamming-Kugel ist, das mit dem Radius auf sich selbst zentriert ist , kann kein Fehlermuster von oder weniger Fehlern ein Codewort in ein anderes ändern. Wenn der Empfänger erkennt, dass der empfangene Vektor kein Codewort von ist , werden die Fehler erkannt (aber keine Garantie für die Korrektur). ${\ displaystyle d-1}$${\ displaystyle c}$${\ displaystyle d-1}$${\ displaystyle d-1}$${\ displaystyle {\ mathcal {C}}}$
• ${\ displaystyle {\ mathcal {C}}}$ kann Fehler korrigieren . Da ein Codewort das einzige Codewort in der Hamming-Kugel ist , die mit dem Radius auf sich selbst zentriert ist, überlappen sich die beiden Hamming-Kugeln, die auf zwei verschiedenen Codewörtern mit beiden Radien zentriert sind, nicht. Wenn wir die Fehlerkorrektur als das Finden des Codeworts betrachten, das dem empfangenen Wort am nächsten liegt , gibt es daher nur ein Codewort in der Hamming-Kugel, die mit dem Radius zentriert ist , so dass alle Fehler korrigiert werden könnten , solange die Anzahl der Fehler nicht größer als ist . ${\ displaystyle \ textstyle \ left \ lfloor {{d-1} \ over 2} \ right \ rfloor}$${\ displaystyle c}$${\ displaystyle d-1}$${\ displaystyle \ textstyle \ left \ lfloor {{d-1} \ over 2} \ right \ rfloor}$${\ displaystyle y}$${\ displaystyle \ textstyle \ left \ lfloor {{d-1} \ over 2} \ right \ rfloor}$${\ displaystyle y}$${\ displaystyle \ textstyle \ left \ lfloor {{d-1} \ over 2} \ right \ rfloor}$
• Um bei mehr als Fehlern zu decodieren, kann eine Listendecodierung oder eine Maximum-Likelihood-Decodierung verwendet werden. ${\ displaystyle (d-1) / 2}$
• ${\ displaystyle {\ mathcal {C}}}$ kann Löschungen korrigieren . Durch Löschen bedeutet dies, dass die Position des gelöschten Symbols bekannt ist. Die Korrektur könnte durch Übergeben der Decodierung erreicht werden: Beim Passieren wird die gelöschte Position mit dem Symbol gefüllt und eine Fehlerkorrektur durchgeführt. Es muss einen Durchgang geben, bei dem die Anzahl der Fehler nicht größer als ist und daher die Löschungen korrigiert werden könnten. ${\ displaystyle d-1}$ ${\ displaystyle q}$${\ displaystyle i ^ {th}}$${\ displaystyle i ^ {th}}$${\ displaystyle \ textstyle \ left \ lfloor {{d-1} \ over 2} \ right \ rfloor}$

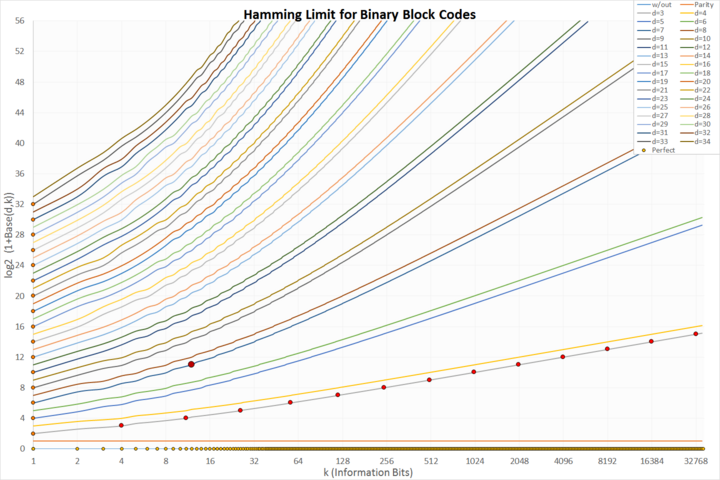
Unter- und Obergrenze von Blockcodes

Hamming-Limit

Es gibt theoretische Grenzen (wie die Hamming-Grenze), aber eine andere Frage ist, welche Codes tatsächlich konstruiert werden können. Es ist, als würde man Kugeln in einer Schachtel in vielen Dimensionen verpacken . Dieses Diagramm zeigt die konstruierbaren Codes, die linear und binär sind. Die x- Achse zeigt die Anzahl der geschützten Symbole k , die y- Achse die Anzahl der benötigten Prüfsymbole n - k . Dargestellt sind die Grenzwerte für verschiedene Hamming-Abstände von 1 (ungeschützt) bis 34. Mit Punkten sind perfekte Codes markiert:

• hellorange auf der x- Achse: triviale ungeschützte Codes
• orange auf der y- Achse: triviale Wiederholungscodes
• dunkelorange im Datensatz d = 3: klassische perfekte Hamming-Codes
• dunkelrot und größer: der einzige perfekte binäre Golay-Code

Familie von Codes

${\ displaystyle C = \ {C_ {i} \} _ {i \ geq 1}}$ wird als Familie von Codes bezeichnet , wobei ein Code mit monotoner Zunahme vorliegt . ${\ displaystyle C_ {i}}$${\ displaystyle (n_ {i}, k_ {i}, d_ {i}) _ {q}}$${\ displaystyle n_ {i}}$

Die Rate der Codefamilie C ist definiert als ${\ displaystyle R (C) = \ lim _ {i \ to \ infty} {k_ {i} \ over n_ {i}}}$

Der relative Abstand der Familie der Codes C ist definiert als ${\ displaystyle \ delta (C) = \ lim _ {i \ to \ infty} {d_ {i} \ over n_ {i}}}$

Um die Beziehung zwischen und zu untersuchen , ist eine Reihe von unteren und oberen Grenzen von Blockcodes bekannt. ${\ displaystyle R (C)}$${\ displaystyle \ delta (C)}$

Hamming gebunden

${\ displaystyle R \ leq 1- {1 \ over n} \ cdot \ log _ {q} \ cdot \ left [\ sum _ {i = 0} ^ {\ left \ lfloor {{\ delta \ cdot n-1 } \ over 2} \ right \ rfloor} {\ binom {n} {i}} (q-1) ^ {i} \ right]}$

Singleton gebunden

Die Singleton-Grenze ist, dass die Summe der Rate und der relativen Entfernung eines Blockcodes nicht viel größer als 1 sein kann:

${\ displaystyle R + \ delta \ leq 1 + {\ frac {1} {n}}}$ .

Mit anderen Worten, jeder Blockcode erfüllt die Ungleichung . Reed-Solomon-Codes sind nicht triviale Beispiele für Codes, die den mit Gleichheit verbundenen Singleton erfüllen. ${\ displaystyle k + d \ leq n + 1}$

Plotkin gebunden

Für , . Mit anderen Worten , . ${\ displaystyle q = 2}$${\ displaystyle R + 2 \ delta \ leq 1}$${\ displaystyle k + 2d \ leq n}$

Für den allgemeinen Fall gelten die folgenden Plotkin-Grenzen für alle mit Abstand d : ${\ displaystyle C \ subseteq \ mathbb {F} _ {q} ^ {n}}$

1. Wenn ${\ displaystyle d = \ left (1- {1 \ over q} \ right) n, | C | \ leq 2qn}$
2. Wenn ${\ displaystyle d> \ left (1- {1 \ over q} \ right) n, | C | \ leq {qd \ over {qd- \ left (q-1 \ right) n}}}$

Für jeden q -ary-Code mit Abstand gilt: ${\ displaystyle \ delta}$${\ displaystyle R \ leq 1- \ left ({q \ over {q-1}} \ right) \ delta + o \ left (1 \ right)}$

Gilbert-Varshamov gebunden

${\ displaystyle R \ geq 1-H_ {q} \ left (\ delta \ right) - \ epsilon}$ , Wo , ist die q - ary Entropiefunktion. ${\ displaystyle 0 \ leq \ delta \ leq 1- {1 \ over q}, 0 \ leq \ epsilon \ leq 1-H_ {q} \ left (\ delta \ right)}$${\ displaystyle H_ {q} \ left (x \ right) ~ {\ overset {\ underset {\ mathrm {def}} {}} {=}} ~ -x \ cdot \ log _ {q} {x \ over {q-1}} - \ left (1-x \ right) \ cdot \ log _ {q} {\ left (1-x \ right)}}$

Johnson gebunden

Definieren . Sei die maximale Anzahl von Codewörtern in einer Hamming-Kugel mit dem Radius e für jeden Code der Entfernung d . ${\ displaystyle J_ {q} \ left (\ delta \ right) ~ {\ overset {\ underset {\ mathrm {def}} {}} {=}} ~ \ left (1- {1 \ over q} \ right ) \ left (1 - {\ sqrt {1- {q \ delta \ over {q-1}}}} \ right)}$
${\ displaystyle J_ {q} \ left (n, d, e \ right)}$${\ displaystyle C \ subseteq \ mathbb {F} _ {q} ^ {n}}$

Dann haben wir die Johnson Bound  : , wenn ${\ displaystyle J_ {q} \ left (n, d, e \ right) \ leq qnd}$${\ displaystyle {e \ over n} \ leq {{q-1} \ over q} \ left ({1 - {\ sqrt {1- {q \ over {q-1}} \ cdot {d \ over n }}}} \, \ right) = J_ {q} \ left ({d \ over n} \ right)}$

Elias-Bassalygo gebunden

${\ displaystyle R = {\ log _ {q} {| C |} \ over n} \ leq 1-H_ {q} \ left (J_ {q} \ left (\ delta \ right) \ right) + o \ links (1 \ rechts)}$

Kugelpackungen und Gitter

Blockcodes sind mit dem Problem der Kugelpackung verbunden, das im Laufe der Jahre einige Aufmerksamkeit erhalten hat. In zwei Dimensionen ist es einfach zu visualisieren. Nehmen Sie ein paar Pfennige flach auf den Tisch und schieben Sie sie zusammen. Das Ergebnis ist ein Sechseckmuster wie ein Bienennest. Blockcodes basieren jedoch auf mehr Dimensionen, die nicht einfach visualisiert werden können. Der leistungsstarke Golay-Code, der in der Weltraumkommunikation verwendet wird, verwendet 24 Dimensionen. Bei Verwendung als Binärcode (was normalerweise der Fall ist) beziehen sich die Abmessungen auf die Länge des oben definierten Codeworts.

Die Codierungstheorie verwendet das N- dimensionale Kugelmodell. Zum Beispiel, wie viele Pennys können auf einer Tischplatte oder in drei Dimensionen in einen Kreis gepackt werden, wie viele Murmeln können in einen Globus gepackt werden. Andere Überlegungen geben die Auswahl eines Codes an. Zum Beispiel lässt das Packen mit Sechsecken in die Beschränkung eines rechteckigen Kastens an den Ecken leeren Raum. Wenn die Abmessungen größer werden, wird der Prozentsatz des leeren Raums kleiner. Bei bestimmten Abmessungen beansprucht die Verpackung jedoch den gesamten Raum und diese Codes sind die sogenannten perfekten Codes. Es gibt nur sehr wenige dieser Codes.

Eine weitere Eigenschaft ist die Anzahl der Nachbarn, die ein einzelnes Codewort haben kann. Betrachten Sie noch einmal Pennies als Beispiel. Zuerst packen wir die Pennys in ein rechteckiges Gitter. Jeder Penny hat 4 nahe Nachbarn (und 4 an den weiter entfernten Ecken). In einem Sechseck hat jeder Penny 6 nahe Nachbarn. In drei und vier Dimensionen wird die maximale Packung durch die 12-Flächen- und 24-Zellen- Packung mit 12 bzw. 24 Nachbarn angegeben. Wenn wir die Dimensionen vergrößern, nimmt die Anzahl der nahen Nachbarn sehr schnell zu. Im Allgemeinen wird der Wert durch die Kusszahlen angegeben .

Das Ergebnis ist, dass die Anzahl der Möglichkeiten für Rauschen, den Empfänger dazu zu bringen, einen Nachbarn auszuwählen (daher ein Fehler), ebenfalls zunimmt. Dies ist eine grundlegende Einschränkung von Blockcodes und in der Tat aller Codes. Es mag schwieriger sein, einem einzelnen Nachbarn einen Fehler zuzufügen, aber die Anzahl der Nachbarn kann groß genug sein, so dass die Gesamtfehlerwahrscheinlichkeit tatsächlich leidet.

Siehe auch

• Kanalkapazität
• Shannon-Hartley-Theorem
• Lauter Kanal
• Listendecodierung
• Kugelverpackung

Verweise

• JH van Lint (1992). Einführung in die Codierungstheorie . GTM . 86 (2. Aufl.). Springer-Verlag. p.  31 . ISBN   3-540-54894-7 .
• FJ MacWilliams ; NJA Sloane (1977). Die Theorie der Fehlerkorrekturcodes . Nordholland. p.  35 . ISBN   0-444-85193-3 .
• W. Huffman; V.Pless (2003). Grundlagen fehlerkorrigierender Codes . Cambridge University Press. ISBN   978-0-521-78280-7 .
• S. Lin; DJ Jr. Costello (1983). Fehlerkontrollcodierung: Grundlagen und Anwendungen . Prentice-Hall. ISBN   0-13-283796-X .

Externe Links

• Charan Langton (2001) Codierungskonzepte und Blockcodierung