Vollständiger zweiteiliger Graph - Complete bipartite graph

Vollständiger zweiteiliger Graph
Ein vollständiger bipartiter Graph mit m = 5 und n = 3
Scheitelpunkte	n + m
Kanten	mn
Radius	${\displaystyle \left\{{\begin{array}{ll}1&m=1\vee n=1\\2&{\text{sonst}}\end{array}}\right.}$
Durchmesser	${\displaystyle \left\{{\begin{array}{ll}1&m=n=1\\2&{\text{sonst}}\end{array}}\right.}$
Umfang	${\displaystyle \left\{{\begin{array}{ll}\infty &m=1\lor n=1\\4&{\text{sonst}}\end{array}}\right.}$
Automorphismen	${\displaystyle \left\{{\begin{array}{ll}2m!n!&n=m\\m!n!&{\text{sonst}}\end{array}}\right.}$
Chromatische Zahl	2
Chromatischer Index	max{ m , n }
Spektrum	${\displaystyle \left\{0^{n+m-2},(\pm {\sqrt {nm}})^{1}\right\}}$
Notation	${\displaystyle K_{m,n}}$
Tabelle mit Grafiken und Parametern

Im mathematischen Bereich der Graphentheorie ist ein vollständiger bipartiter Graph oder eine Biclique eine besondere Art von bipartiten Graphen, bei denen jeder Knoten der ersten Menge mit jedem Knoten der zweiten Menge verbunden ist.

Die Graphentheorie selbst wird typischerweise mit Leonhard Eulers Werk von 1736 über die Sieben Brücken von Königsberg datiert . Allerdings Zeichnungen von kompletter bipartite Graphen wurden bereits gedruckt bereits 1669 im Zusammenhang mit einer Ausgabe der Werke von Ramon Llull bearbeitet von Athanasius Kircher . Llull selbst hatte drei Jahrhunderte zuvor ähnliche Zeichnungen vollständiger Graphen angefertigt .

Definition

Ein vollständiger bipartiter Graph ist ein Graph, dessen Knoten in zwei Teilmengen V ₁ und V _{2 unterteilt werden können} , sodass keine Kante beide Endpunkte in derselben Teilmenge hat und jede mögliche Kante, die Knoten in verschiedenen Teilmengen verbinden könnte, Teil des Graphen ist. Das heißt, es ist ein zweiteiliger Graph ( V ₁ , V ₂ , E ) derart , daß für alle zwei Eckpunkte v ₁ ∈ V ₁ und V ₂ ∈ V ₂ , V ₁ V ₂ ist eine Kante in E . Ein vollständiger bipartiter Graph mit Partitionen der Größe | V ₁ | = m und | V ₂ | = n , wird mit Km _{,n bezeichnet} ; alle zwei Graphen mit der gleichen Notation sind isomorph .

Beispiele

Die Sterndiagramme K _1,3 , K _1,4 , K _1,5 und K _1,6 .

Ein vollständiger zweiteiliger Graph von K _{4,7, der} zeigt, dass Turáns Ziegelwerksproblem mit 4 Lagerstätten (gelbe Punkte) und 7 Öfen (blaue Punkte) 18 Kreuzungen (rote Punkte) erfordert.

• Für jedes k , K _{1 heißt k} ein Stern . Alle vollständigen bipartiten Graphen, die Bäume sind , sind Sterne.
  • Der Graph K _1,3 wird als Klaue bezeichnet und dient zur Definition der klauenfreien Graphen .
• Der Graph K _3,3 wird als Nutzengraph bezeichnet . Diese Verwendung stammt aus einem mathematischen Standardrätsel, bei dem drei Versorgungsunternehmen jeweils mit drei Gebäuden verbunden werden müssen; eine Lösung ohne Kreuzungen ist wegen der Nichtplanarität von K _{3,3 nicht möglich} .
• Die maximalen Bicliquen, die als Teilgraphen des Digraphen einer Relation gefunden werden, werden Konzepte genannt . Wenn ein Gitter durch Treffen und Verbinden dieser Teilgraphen gebildet wird, hat die Beziehung ein induziertes Konzeptgitter . Diese Art der Beziehungsanalyse wird als formale Konzeptanalyse bezeichnet .

Eigenschaften

Beispiel K _{p , p} vollständige bipartite Graphen

K 3,3	K 4,4	K 5,5
3 Kantenfärbungen	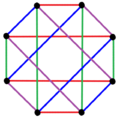4 Kantenfärbungen	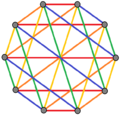5 Kantenfärbungen
Regelmäßige komplexe Polygone der Form 2{4} p haben vollständige bipartite Graphen mit 2 p Ecken (rot und blau) und p 2 2-Kanten. Sie können auch als p -Kantenfärbungen gezeichnet werden .

• Bei einem gegebenen bipartiten Graphen ist die Prüfung, ob er einen vollständigen bipartiten Teilgraphen K _{i , i} für einen Parameter  i enthält, ein NP-vollständiges Problem.
• Ein planarer Graph kann nicht enthalten K _3,3 als minor ; ein äußererplanarer Graph kann K _{3,2 nicht} als Minor enthalten (dies sind keine hinreichenden Bedingungen für Planarität und äußere Planarität, aber notwendig). Umgekehrt enthält jeder nichtplanare Graph entweder K _3,3 oder den vollständigen Graphen K ₅ als Minor; Dies ist der Satz von Wagner .
• Jeder vollständige bipartite Graph. K _{n , n} ist ein Moore-Graphen und ein ( n ,4) -Käfig .
• Die vollständigen bipartiten Graphen K _{n , n} und K _{n , n +1} haben die maximal mögliche Kantenzahl unter allen dreiecksfreien Graphen mit gleicher Knotenzahl; das ist Mantels Theorem . Mantels Ergebnis wurde auf k- partite Graphen und Graphen verallgemeinert , die größere Cliquen als Untergraphen im Satz von Turán vermeiden , und diese beiden vollständigen bipartiten Graphen sind Beispiele für Turán-Graphen , die Extremalgraphen für dieses allgemeinere Problem.
• Der vollständige bipartite Graph K _{m , n} hat eine Eckenüberdeckungszahl von min { m , n } und eine Kantenüberdeckungszahl von max { m , n }.
• Der vollständige bipartite Graph K _{m , n} hat eine maximale unabhängige Menge der Größe max { m , n }.
• Die Adjazenzmatrix eines vollständigen bipartiten Graphen K _{m , n} hat Eigenwerte √ nm , − √ nm und 0; mit Multiplizität 1, 1 bzw. n + m –2.
• Die Laplace-Matrix eines vollständigen bipartiten Graphen K _{m , n} hat Eigenwerte n + m , n , m und 0; mit Multiplizität 1, m −1, n −1 bzw. 1.
• Ein vollständiger bipartiter Graph K _{m , n} hat m ^{n −1} n ^{m −1} aufspannende Bäume .
• Ein vollständiger bipartiter Graph K _{m , n} hat ein maximales Matching der Größe min { m , n }.
• Ein vollständiger bipartiter Graph K _{n , n} hat eine echte n -Kantenfärbung , die einem lateinischen Quadrat entspricht .
• Jeder vollständige bipartite Graph ist ein modularer Graph : Jedes Knotentripel hat einen Median, der zu den kürzesten Wegen zwischen jedem Knotenpaar gehört.

Siehe auch

• Biclique-freier Graph , eine Klasse von dünn besetzten Graphen , die durch die Vermeidung vollständiger bipartiter Teilgraphen definiert wird
• Kronengraph , ein Graph, der durch Entfernen eines perfekten Matchings aus einem vollständigen bipartiten Graphen gebildet wird
• Vollständiger multipartiter Graph , eine Verallgemeinerung vollständiger bipartiter Graphen auf mehr als zwei Sätze von Knoten
• Biclique-Angriff

Verweise