Komplexe Analyse -Complex analysis

Mathematische Analyse → Komplexe Analyse
Komplexe Analyse
Komplexe Zahlen
Reelle Zahl Imaginäre Zahl Komplexes Flugzeug Komplex konjugiert Komplexe Einheitszahl
Komplexe Funktionen
Komplexwertige Funktion Analytische Funktion Holomorphe Funktion Cauchy-Riemann-Gleichungen Formale Potenzreihe
Grundlegende Theorie
Nullen und Pole Integralsatz von Cauchy Lokales Primitiv Cauchys Integralformel Wicklungsnummer Laurent-Reihe Isolierte Singularität Restsatz Konforme Karte Schwarz-Lemma Harmonische Funktion Laplace-Gleichung
Theorie der geometrischen Funktionen
Menschen
Augustin-Louis Cauchy Leonhard Euler Carl Friedrich Gauß Jaques Hadamard Kiyoshi Oka Bernhard Riemann Karl Weierstraß
Mathematik-Portal
v T e

Die Komplexanalyse , traditionell als Theorie der Funktionen einer komplexen Variablen bekannt , ist der Zweig der mathematischen Analyse , der Funktionen komplexer Zahlen untersucht . Es ist in vielen Zweigen der Mathematik hilfreich, einschließlich algebraischer Geometrie , Zahlentheorie , analytischer Kombinatorik , angewandter Mathematik ; sowie in der Physik , einschließlich der Zweige der Hydrodynamik , Thermodynamik und insbesondere der Quantenmechanik . Durch die Erweiterung hat die Verwendung komplexer Analysen auch Anwendungen in technischen Bereichen wie Nuklear- , Luft- und Raumfahrt- , Maschinenbau- und Elektrotechnik .

Da eine differenzierbare Funktion einer komplexen Variablen gleich ihrer Taylor-Reihe ist (d. h. sie ist analytisch ), befasst sich die komplexe Analyse insbesondere mit analytischen Funktionen einer komplexen Variablen (d. h. holomorphen Funktionen ).

Geschichte

Augustin-Louis Cauchy , einer der Begründer der Komplexanalyse

Die komplexe Analysis ist einer der klassischen Zweige der Mathematik mit Wurzeln im 18. Jahrhundert und kurz davor. Wichtige Mathematiker, die mit komplexen Zahlen in Verbindung gebracht werden, sind Euler , Gauß , Riemann , Cauchy , Gösta Mittag-Leffler , Weierstraß und viele mehr im 20. Jahrhundert. Die Komplexanalyse, insbesondere die Theorie der konformen Abbildungen , hat viele physikalische Anwendungen und wird auch in der gesamten analytischen Zahlentheorie verwendet . In der heutigen Zeit ist es sehr populär geworden durch einen neuen Aufschwung durch komplexe Dynamik und die Bilder von Fraktalen , die durch iterierende holomorphe Funktionen erzeugt werden . Eine weitere wichtige Anwendung der Komplexanalyse ist die Stringtheorie , die konforme Invarianten in der Quantenfeldtheorie untersucht .

Komplexe Funktionen

Eine Exponentialfunktion A ⁿ einer diskreten ( ganzzahligen ) Variablen n , ähnlich der geometrischen Progression

Eine komplexe Funktion ist eine Funktion von komplexen Zahlen zu komplexen Zahlen. Mit anderen Worten, es ist eine Funktion, die eine Teilmenge der komplexen Zahlen als Domäne und die komplexen Zahlen als Kodomäne hat . Komplexe Funktionen sollen im Allgemeinen eine Domäne haben, die eine nicht leere offene Teilmenge der komplexen Ebene enthält .

Für jede komplexe Funktion können die Werte aus dem Bereich und ihre Bilder im Bereich in Real- und Imaginärteile getrennt werden : ${\displaystyle z}$${\displaystyle f(z)}$

${\displaystyle z=x+iy\quad {\text{ und }}\quad f(z)=f(x+iy)=u(x,y)+iv(x,y),}$

wo sind alle reell bewertet. ${\displaystyle x,y,u(x,y),v(x,y)}$

Mit anderen Worten, eine komplexe Funktion kann in zerlegt werden ${\displaystyle f:\mathbb {C} \to \mathbb {C} }$

${\displaystyle u:\mathbb {R} ^{2}\to \mathbb {R} \quad }$Und${\displaystyle \quad v:\mathbb {R} ^{2}\to \mathbb {R} ,}$

dh in zwei reellwertige Funktionen ( , ) zweier reeller Variablen ( , ). ${\displaystyle u}$${\displaystyle v}$${\ displaystyle x}$${\displaystyle y}$

In ähnlicher Weise kann jede komplexwertige Funktion f auf einer beliebigen Menge X (ist isomorph zu und daher in diesem Sinne) als ein geordnetes Paar von zwei reellwertigen Funktionen betrachtet werden : (Re f , Im f ) oder alternativ als vektorwertige Funktion von X in${\displaystyle \mathbb {R} ^{2}.}$

Einige Eigenschaften komplexwertiger Funktionen (wie Stetigkeit ) sind nichts anderes als die entsprechenden Eigenschaften vektorwertiger Funktionen zweier reeller Variablen. Andere Konzepte der komplexen Analysis, wie z. B. Differenzierbarkeit , sind direkte Verallgemeinerungen ähnlicher Konzepte für reelle Funktionen, können aber sehr unterschiedliche Eigenschaften haben. Insbesondere ist jede differenzierbare komplexe Funktion analytisch (siehe nächster Abschnitt), und zwei differenzierbare Funktionen, die in der Umgebung eines Punktes gleich sind, sind am Schnittpunkt ihres Bereichs gleich (wenn die Bereiche verbunden sind ). Die letztere Eigenschaft ist die Grundlage des Prinzips der analytischen Fortsetzung , das es ermöglicht, jede reelle analytische Funktion auf einzigartige Weise zu erweitern, um eine komplexe analytische Funktion zu erhalten, deren Domäne die gesamte komplexe Ebene mit einer endlichen Anzahl entfernter Kurvenbögen ist. Viele grundlegende und spezielle komplexe Funktionen werden auf diese Weise definiert, einschließlich der komplexen Exponentialfunktion , der komplexen Logarithmusfunktionen und der trigonometrischen Funktionen .

Holomorphe Funktionen

Komplexe Funktionen, die an jedem Punkt einer offenen Teilmenge der komplexen Ebene differenzierbar sind , heißen auf holomorph . Im Zusammenhang mit der komplexen Analyse wird die Ableitung von at als definiert ${\displaystyle \Omega}$ ${\displaystyle \Omega}$${\displaystyle f}$${\displaystyle z_{0}}$

${\displaystyle f'(z_{0})=\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}} .}$

Oberflächlich betrachtet ist diese Definition formal analog zu der der Ableitung einer reellen Funktion. Komplexe Ableitungen und differenzierbare Funktionen verhalten sich jedoch deutlich anders als ihre realen Gegenstücke. Damit diese Grenze existiert, muss insbesondere der Wert des Differenzenquotienten sich der gleichen komplexen Zahl annähern, unabhängig davon, wie wir uns in der komplexen Ebene nähern. Folglich hat komplexe Differenzierbarkeit viel stärkere Implikationen als echte Differenzierbarkeit. Beispielsweise sind holomorphe Funktionen unendlich differenzierbar , während die Existenz der n -ten Ableitung nicht die Existenz der ( n + 1)-ten Ableitung für reelle Funktionen implizieren muss. Darüber hinaus erfüllen alle holomorphen Funktionen die stärkere Bedingung der Analytizität , was bedeutet, dass die Funktion an jedem Punkt ihres Wirkungsbereichs lokal durch eine konvergente Potenzreihe gegeben ist. Im Wesentlichen bedeutet dies, dass Funktionen, die auf holomorph sind, beliebig gut durch Polynome in irgendeiner Umgebung jedes Punktes in angenähert werden können . Dies steht in scharfem Gegensatz zu differenzierbaren reellen Funktionen; es gibt unendlich differenzierbare reelle Funktionen, die nirgends analytisch sind; siehe Nicht-analytische glatte Funktion § Eine glatte Funktion, die nirgendwo wirklich analytisch ist . ${\displaystyle z_{0}}$${\displaystyle \Omega}$${\displaystyle \Omega}$

Die meisten elementaren Funktionen, einschließlich der Exponentialfunktion , der trigonometrischen Funktionen und aller Polynomfunktionen , die entsprechend zu komplexen Argumenten als Funktionen erweitert werden , sind über die gesamte komplexe Ebene holomorph, was sie zu vollständigen Funktionen macht , während rationale Funktionen , wobei p und q Polynome sind, sind auf Gebieten holomorph, die Punkte ausschließen, an denen q null ist. Solche Funktionen, die überall außer einer Menge isolierter Punkte holomorph sind, werden als meromorphe Funktionen bezeichnet . Andererseits sind die Funktionen , , und nirgendwo auf der komplexen Ebene holomorph, wie man daran erkennen kann, dass sie die Cauchy-Riemann-Bedingungen nicht erfüllen (siehe unten). ${\displaystyle \mathbb {C} \to \mathbb {C} }$ ${\displaystyle p/q}$${\displaystyle z\mapsto \Re (z)}$ ${\displaystyle z\mapsto |z|}$${\displaystyle z\mapsto {\bar {z}}}$

Eine wichtige Eigenschaft holomorpher Funktionen ist die Beziehung zwischen den partiellen Ableitungen ihrer reellen und imaginären Komponenten, die als Cauchy-Riemann-Bedingungen bekannt sind . Wenn , definiert durch , wobei , auf einer Region holomorph ist , dann gilt für alle , ${\displaystyle f:\mathbb {C} \to \mathbb {C} }$${\displaystyle f(z)=f(x+iy)=u(x,y)+iv(x,y)}$${\displaystyle x,y,u(x,y),v(x,y)\in \mathbb {R} }$ ${\displaystyle \Omega}$${\displaystyle z_{0}\in \Omega}$

${\displaystyle {\frac {\partial f}{\partial {\bar {z}}}}(z_{0})=0,\ {\text{where }}{\frac {\partial }{\partial {\bar {z}}}}\mathrel {:=} {\frac {1}{2}}\left({\frac {\partial }{\partial x}}+i{\frac {\partial } {\partial y}}\right).}$

In Bezug auf den Real- und Imaginärteil der Funktion u und v entspricht dies dem Gleichungspaar und , wobei die Indizes eine partielle Differenzierung anzeigen. Die Cauchy-Riemann-Bedingungen charakterisieren jedoch keine holomorphen Funktionen ohne zusätzliche Stetigkeitsbedingungen (siehe Satz von Looman-Menchoff ). ${\displaystyle u_{x}=v_{y}}$${\displaystyle u_{y}=-v_{x}}$

Holomorphe Funktionen weisen einige bemerkenswerte Merkmale auf. Zum Beispiel behauptet der Satz von Picard , dass der Wertebereich einer ganzen Funktion nur drei mögliche Formen annehmen kann: , , oder für einige . Mit anderen Worten, wenn zwei verschiedene komplexe Zahlen und nicht im Bereich einer ganzen Funktion liegen , dann ist eine konstante Funktion. Darüber hinaus wird eine holomorphe Funktion auf einer verbundenen offenen Menge durch ihre Beschränkung auf eine beliebige nicht leere offene Teilmenge bestimmt. ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} \setminus \{z_{0}\}}$${\displaystyle \{z_{0}\}}$${\displaystyle z_{0}\in \mathbb {C} }$${\displaystyle z}$${\displaystyle w}$${\displaystyle f}$${\displaystyle f}$

Konforme Karte

Dieser Abschnitt ist ein Auszug aus Conformal map . [ bearbeiten ]

Ein rechteckiges Gitter (oben) und sein Bild unter einer konformen Karte (unten). Es ist ersichtlich, dass Linienpaare, die sich bei 90° schneiden, auf Kurvenpaare abgebildet werden, die sich immer noch bei 90° schneiden.${\displaystyle f}$${\displaystyle f}$

In der Mathematik ist eine konforme Abbildung eine Funktion , die lokal Winkel bewahrt , aber nicht unbedingt Längen.

Formeller ausgedrückt, sei und sei eine offene Teilmenge von . Eine Funktion wird an einem Punkt als konform (oder winkelerhaltend) bezeichnet, wenn sie Winkel zwischen gerichteten Kurven durch sowie die Orientierung beibehält. Konforme Karten bewahren sowohl Winkel als auch die Formen unendlich kleiner Figuren, aber nicht unbedingt ihre Größe oder Krümmung . ${\displaystyle U}$${\displaystyle V}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle f:U\bis V}$${\displaystyle u_{0}\in U}$${\displaystyle u_{0}}$

Die konforme Eigenschaft kann durch die Jacobi- Ableitungsmatrix einer Koordinatentransformation beschrieben werden . Die Transformation ist immer dann winkeltreu, wenn der Jacobi an jedem Punkt ein positiver Skalar multipliziert mit einer Rotationsmatrix ( orthogonal mit Determinante eins) ist. Einige Autoren definieren Konformität, um orientierungsumkehrende Abbildungen einzuschließen, deren Jacobianer als beliebige Skalar mal beliebige orthogonale Matrix geschrieben werden können.

Für Abbildungen in zwei Dimensionen sind die (orientierungserhaltenden) konformen Abbildungen genau die lokal invertierbaren komplexen analytischen Funktionen. In drei und höheren Dimensionen begrenzt der Satz von Liouville die konformen Abbildungen scharf auf einige wenige Typen.

Der Begriff der Konformität lässt sich auf natürliche Weise auf Abbildungen zwischen Riemannschen oder semi-Riemannschen Mannigfaltigkeiten verallgemeinern .

Wichtige Ergebnisse

Farbkreisdiagramm der Funktion f ( x ) = ( x ² − 1)( x − 2 − ich ) ²/x ² + 2 + 2 ich.
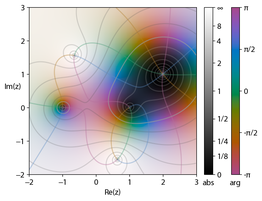
Der Farbton stellt das Argument dar , die Helligkeit die Größe.

Eines der zentralen Werkzeuge in der komplexen Analysis ist das Linienintegral . Das Linienintegral um einen geschlossenen Pfad einer Funktion, die überall innerhalb der durch den geschlossenen Pfad begrenzten Fläche holomorph ist, ist immer Null, wie es der Integralsatz von Cauchy aussagt . Die Werte einer solchen holomorphen Funktion innerhalb einer Scheibe können durch ein Pfadintegral auf dem Rand der Scheibe berechnet werden (wie in der Integralformel von Cauchy gezeigt ). Wegintegrale in der komplexen Ebene werden oft zur Bestimmung komplizierter reeller Integrale verwendet, wobei hier unter anderem die Residuentheorie anwendbar ist (siehe Methoden der Konturintegration ). Ein "Pol" (oder isolierte Singularität ) einer Funktion ist ein Punkt, an dem der Wert der Funktion unbegrenzt wird oder "explodiert". Wenn eine Funktion einen solchen Pol hat, kann man dort das Residuum der Funktion berechnen, das verwendet werden kann, um Pfadintegrale zu berechnen, an denen die Funktion beteiligt ist. das ist der Inhalt des mächtigen Residuensatzes . Das bemerkenswerte Verhalten holomorpher Funktionen in der Nähe wesentlicher Singularitäten wird durch den Satz von Picard beschrieben . Funktionen, die nur Pole, aber keine wesentlichen Singularitäten haben, heißen meromorph . Laurent-Reihen sind das komplexwertige Äquivalent zu Taylor-Reihen , können aber verwendet werden, um das Verhalten von Funktionen in der Nähe von Singularitäten durch unendliche Summen besser verstandener Funktionen wie Polynome zu untersuchen.

Eine beschränkte Funktion , die in der gesamten komplexen Ebene holomorph ist, muss konstant sein; das ist der Satz von Liouville . Es kann verwendet werden, um einen natürlichen und kurzen Beweis für den Fundamentalsatz der Algebra zu liefern , der besagt, dass der Körper der komplexen Zahlen algebraisch abgeschlossen ist .

Wenn eine Funktion in einem verbundenen Bereich holomorph ist, werden ihre Werte vollständig durch ihre Werte in einem kleineren Teilbereich bestimmt. Die Funktion auf dem größeren Bereich soll aus ihren Werten auf dem kleineren Bereich analytisch fortgesetzt werden. Dies ermöglicht die Erweiterung der Definition von Funktionen, wie der Riemannschen Zeta-Funktion , die zunächst als unendliche Summen definiert sind, die nur auf begrenzten Gebieten konvergieren, auf fast die gesamte komplexe Ebene. Manchmal, wie im Fall des natürlichen Logarithmus , ist es unmöglich, eine holomorphe Funktion analytisch auf einen nicht einfach verbundenen Bereich in der komplexen Ebene fortzusetzen, aber es ist möglich, sie zu einer holomorphen Funktion auf einer eng verwandten Oberfläche, die als a bekannt ist, zu erweitern Riemannsche Fläche .

All dies bezieht sich auf eine komplexe Analyse in einer Variablen. Es gibt auch eine sehr reichhaltige Theorie der komplexen Analyse in mehr als einer komplexen Dimension, in der die analytischen Eigenschaften wie Potenzreihenentwicklung übertragen werden, während die meisten geometrischen Eigenschaften holomorpher Funktionen in einer komplexen Dimension (z. B. Konformität ) nicht übertragen werden . Der Abbildungssatz von Riemann über die konforme Beziehung bestimmter Bereiche in der komplexen Ebene, der möglicherweise das wichtigste Ergebnis der eindimensionalen Theorie ist, versagt dramatisch in höheren Dimensionen.

Eine Hauptanwendung bestimmter komplexer Räume liegt in der Quantenmechanik als Wellenfunktionen .

Siehe auch

• Komplexe Geometrie
• Hyperkomplexe Analyse
• Vektorrechnung
• Liste komplexer Analysethemen
• Satz der Monodromie
• Echte Analyse
• Satz von Riemann-Roch
• Satz von Runge

Verweise

Quellen

• Ablowitz, MJ & AS Fokas , Komplexe Variablen: Einführung und Anwendungen (Cambridge, 2003).
• Ahlfors, L. , Komplexe Analyse (McGraw-Hill, 1953).
• Cartan, H. , Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes. (Hermann, 1961). Englische Übersetzung, Elementary Theory of Analytic Functions of One or Multiple Complex Variables. (Addison-Wesley, 1963).
• Carathéodory, C. , Funktionentheorie. (Birkhäuser, 1950). Englische Übersetzung, Theory of Functions of a Complex Variable (Chelsea, 1954). [2 Bände.]
• Carrier, GF , M. Krook , & CE Pearson, Funktionen einer komplexen Variablen: Theorie und Technik. (McGraw-Hill, 1966).
• Conway, JB , Funktionen einer komplexen Variablen. (Springer, 1973).
• Fisher, S., Komplexe Variablen. (Wadsworth & Brooks/Cole, 1990).
• Forsyth, A. , Theorie der Funktionen einer komplexen Variablen (Cambridge, 1893).
• Freitag, E. & R. Busam, Funktionentheorie . (Springer, 1995). Englische Übersetzung, Komplexe Analyse . (Springer, 2005).
• Goursat, E. , Cours d'analyse mathématique, Band 2 . (Gauthier-Villars, 1905). Englische Übersetzung, Ein Kurs der mathematischen Analyse, vol. 2, Teil 1: Funktionen einer komplexen Variablen . (Gin, 1916).
• Henrici, P. , Angewandte und Computerkomplexanalyse (Wiley). [Drei Bände: 1974, 1977, 1986.]
• Kreyszig, E. , Höhere Ingenieurmathematik. (Wiley, 1962).
• Lavrentyev, M. & B. Shabat, Методы теории функций комплексного переменного. ( Methoden der Theorie der Funktionen einer komplexen Variablen ). (1951, auf Russisch).
• Markushevich, AI , Theorie der Funktionen einer komplexen Variablen , (Prentice-Hall, 1965). [Drei Bände.]
• Marsden & Hoffman, Grundkomplexanalyse. (Freemann, 1973).
• Needham, T. , Visuelle komplexe Analyse. (Oxford, 1997). http://usf.usfca.edu/vca/
• Remmert, R. , Theorie komplexer Funktionen . (Springer, 1990).
• Rudin, W. , Reelle und Komplexe Analysis. (McGraw-Hill, 1966).
• Shaw, WT, Komplexe Analyse mit Mathematica (Cambridge, 2006).
• Stein, E. & R. Shakarchi, Komplexe Analyse. (Princeton, 2003).
• Sveshnikov, AG & AN Tikhonov , Теория функций комплексной переменной. (Nauka, 1967). Englische Übersetzung, Die Theorie der Funktionen einer komplexen Variablen (MIR, 1978).
• Titchmarsh, EC , Die Theorie der Funktionen. (Oxford, 1932).
• Wegert, E., Visuelle komplexe Funktionen . (Birkhäuser, 2012).
• Whittaker, ET & GN Watson , Ein Kurs der modernen Analyse . (Cambridge, 1902). 3. Aufl. (1920)

Externe Links

• Komplexe Analyseseite MathWorld von Wolfram Research