Satz von De Moivre-Laplace - De Moivre–Laplace theorem

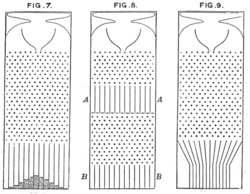
Innerhalb eines Systems, dessen Behälter gemäß der Binomialverteilung gefüllt sind (wie Galtons " Bohnenmaschine ", hier gezeigt), gegeben eine ausreichende Anzahl von Versuchen (hier die Reihen von Stiften, von denen jede eine fallengelassene "Bohne" in Richtung links oder rechts), eine Form, die die Wahrscheinlichkeitsverteilung von k Erfolgen in n Versuchen darstellt (siehe unten in Abb. 7) stimmt ungefähr mit der Gaußschen Verteilung mit Mittelwert np und Varianz np (1− p ) überein , vorausgesetzt, die Versuche sind unabhängig und die Erfolge mit Wahrscheinlichkeit p auftreten .

Betrachten Sie, einen Satz von n Münzen sehr oft zu werfen und die Anzahl der "Kopf" zu zählen, die jedes Mal resultieren. Die mögliche Anzahl von Köpfen bei jedem Wurf, k , verläuft von 0 bis n entlang der horizontalen Achse, während die vertikale Achse die relative Häufigkeit des Auftretens des Ergebnisses k Köpfe darstellt. Die Höhe jedes Punktes ist somit die Wahrscheinlichkeit, beim Werfen von n Münzen k Kopf zu beobachten (eine Binomialverteilung basierend auf n Versuchen). Nach dem Satz von de Moivre-Laplace konvergiert die Form der diskreten Verteilung mit zunehmendem n gegen die kontinuierliche Gaußsche Kurve der Normalverteilung .

In der Wahrscheinlichkeitstheorie besagt der de Moivre-Laplace-Satz , der ein Spezialfall des zentralen Grenzwertsatzes ist , dass die Normalverteilung unter bestimmten Bedingungen als Näherung an die Binomialverteilung verwendet werden kann. Insbesondere zeigt das Theorem, dass die Wahrscheinlichkeitsmassenfunktion der Zufallszahl von "Erfolgen", die in einer Reihe unabhängiger Bernoulli-Versuche beobachtet wurden , von denen jeder eine Erfolgswahrscheinlichkeit hat (eine Binomialverteilung mit Versuchen), gegen die Wahrscheinlichkeitsdichtefunktion der Normalen Verteilung mit Mittelwert und Standardabweichung , wie groß wird, unter der Annahme, dass nicht oder ist . ${\displaystyle n}$ ${\displaystyle p}$${\displaystyle n}$${\displaystyle np}$${\textstyle {\sqrt {np(1-p)}}}$${\displaystyle n}$${\displaystyle p}$${\displaystyle 0}$${\displaystyle 1}$

Das Theorem erschien in der zweiten Auflage von The Doctrine of Chances by Abraham de Moivre , veröffentlicht im Jahr 1738. Obwohl de Moivre den Begriff "Bernoulli-Versuche" nicht verwendete, schrieb er über die Wahrscheinlichkeitsverteilung der Häufigkeit, mit der "Köpfe" erscheinen, wenn eine Münze wird 3600 Mal geworfen.

Dies ist eine Ableitung der speziellen Gaußschen Funktion, die in der Normalverteilung verwendet wird.

Satz

Wenn n groß wird, können wir für k in der Umgebung von np approximieren

${\displaystyle {n \choose k}\,p^{k}q^{nk}\simeq {\frac {1}{\sqrt {2\pi npq}}}\,e^{-{\frac { (k-np)^{2}}{2npq}}},\qquad p+q=1,\ p,q>0}$

in dem Sinne, dass das Verhältnis der linken zur rechten Seite für n → ∞ gegen 1 konvergiert .

Beweis

Der Satz kann wie folgt strenger formuliert werden: , mit einer binomial verteilten Zufallsvariablen, nähert sich der Standardnormalen als , wobei das Verhältnis der Wahrscheinlichkeitsmasse von zur Grenznormalendichte 1 ist. Dies kann für eine beliebige von null verschiedene und endliche . gezeigt werden Punkt . Auf der unskalierten Kurve für wäre dies ein Punkt mit ${\displaystyle \left(X\!\,-\!\,np\right)\!/\!{\sqrt {npq}}}$${\displaystyle \textstyle X}$${\displaystyle n\!\to \!\infty }$${\displaystyle X}$${\displaystyle c}$${\displaystyle X}$${\displaystyle k}$

${\displaystyle k=np+c{\sqrt {npq}}}$

Bei 3 bleiben beispielsweise 3 Standardabweichungen vom Mittelwert in der unskalierten Kurve. ${\displaystyle c}$${\displaystyle k}$

Die Normalverteilung mit Mittelwert und Standardabweichung wird durch die Differentialgleichung (DE) definiert ${\displaystyle\mu}$${\displaystyle \sigma}$

${\displaystyle f'\!(x)\!=\!-\!\,{\frac {x-\mu }{\sigma^{2}}}f(x)}$mit der durch das Wahrscheinlichkeitsaxiom festgelegten Anfangsbedingung .${\displaystyle \int_{-\infty}^{\infty}\!f(x)\,dx\!=\!1}$

Die Binomialverteilungsgrenze nähert sich der Normalen, wenn die Binomialverteilung dieses DE erfüllt. Da das Binomial diskret ist, beginnt die Gleichung als Differenzengleichung, deren Grenzwert zu einem DE wird. Differenzengleichungen verwenden die diskrete Ableitung , , die Änderung für die Schrittweite 1. Aus der diskreten Ableitung wird die kontinuierliche Ableitung . Somit braucht der Beweis nur zu zeigen, dass für die unskalierte Binomialverteilung ${\displaystyle \textstyle p(k\!+\!1)\!-\!p(k)}$${\displaystyle \textstyle n\!\to \!\infty }$

${\displaystyle {\frac {f'\!(x)}{f\!(x)}}\!\cdot \!\left(-{\frac {\sigma ^{2}}{x-\mu }}\rechts)\!\nach \!1}$als .${\displaystyle n\!\to \!\infty }$

Das gewünschte Ergebnis kann direkt angezeigt werden:

${\displaystyle {\begin{ausgerichtet}{\frac {f'\!(x)}{f\!(x)}}{\frac {npq}{np\!\,-\!\,k}} \!&={\frac {p\left(n,k+1\right)-p\left(n,k\right)}{p\left(n,k\right)}}{\frac {\ sqrt {npq}}{-c}}\\&={\frac {np-kq}{kq+q}}{\frac {\sqrt {npq}}{-c}}\\&={\frac {-c{\sqrt {npq}}-q}{npq+cq{\sqrt {npq}}+q}}{\frac {\sqrt {npq}}{-c}}\\&\to 1\ Ende{ausgerichtet}}}$

Letzteres gilt, weil der Term sowohl den Nenner als auch den Zähler dominiert als . ${\displaystyle -cnpq}$${\displaystyle n\!\to \!\infty }$

Da nur ganzzahlige Werte angenommen werden, unterliegt die Konstante einem Rundungsfehler. Das Maximum dieses Fehlers ist jedoch ein verschwindender Wert. ${\displaystyle \textstyle k}$${\displaystyle \textstyle c}$${\displaystyle \textstyle {0.5}/\!{\sqrt {npq}}}$

Alternativer Beweis

Der Beweis besteht darin, die linke Seite (in der Aussage des Satzes) durch drei Näherungen auf die rechte Seite zu transformieren.

Zunächst kann nach der Stirling-Formel die Fakultät einer großen Zahl n durch die Näherung

${\displaystyle n!\simeq n^{n}e^{-n}{\sqrt {2\pi n}}\qquad {\text{as }}n\to \infty .}$

So

${\displaystyle {\begin{aligned}{n \choose k}p^{k}q^{nk}&={\frac {n!}{k!(nk)!}}p^{k}q^ {nk}\\&\simeq {\frac {n^{n}e^{-n}{\sqrt {2\pi n}}}{k^{k}e^{-k}{\sqrt { 2\pi k}}(nk)^{nk}e^{-(nk)}{\sqrt {2\pi (nk)}}}}p^{k}q^{nk}\\&={ \sqrt {\frac {n}{2\pi k\left(nk\right)}}}{\frac {n^{n}}{k^{k}\left(nk\right)^{nk} }}p^{k}q^{nk}\\&={\sqrt {\frac {n}{2\pi k\left(nk\right)}}}\left({\frac {np}{ k}}\right)^{k}\left({\frac {nq}{nk}}\right)^{nk}\end{ausgerichtet}}}$

Als nächstes wird die Approximation verwendet, um die Wurzel oben mit der gewünschten Wurzel auf der rechten Seite abzugleichen. ${\displaystyle {\tfrac {k}{n}}\to p}$

${\displaystyle {\begin{aligned}{n \choose k}p^{k}q^{nk}&\simeq {\sqrt {\frac {1}{2\pi n{\frac {k}{n }}\left(1-{\frac {k}{n}}\right)}}}\left({\frac {np}{k}}\right)^{k}\left({\frac { nq}{nk}}\right)^{nk}\\&\simeq {\frac {1}{\sqrt {2\pi npq}}}\left({\frac {np}{k}}\right )^{k}\left({\frac{nq}{nk}}\right)^{nk}\qquad p+q=1\\\end{ausgerichtet}}}$

Schließlich wird der Ausdruck exponentiell umgeschrieben und die Taylor-Reihen-Approximation für ln(1+x) verwendet:

${\displaystyle \ln \left(1+x\right)\simeq x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots }$

Dann

${\displaystyle {\begin{aligned}{n \choose k}p^{k}q^{nk}&\simeq {\frac {1}{\sqrt {2\pi npq}}}\exp \left\ {\ln \left(\left({\frac {np}{k}}\right)^{k}\right)+\ln \left(\left({\frac {nq}{nk}}\right )^{nk}\right)\right\}\\&={\frac {1}{\sqrt {2\pi npq}}}\exp \left\{-k\ln \left({\frac { k}{np}}\right)+(kn)\ln \left({\frac {nk}{nq}}\right)\right\}\\&={\frac {1}{\sqrt {2 \pi npq}}}\exp \left\{-k\ln \left({\frac {np+x{\sqrt {npq}}}{np}}\right)+(kn)\ln \left( {\frac {n-np-x{\sqrt {npq}}}{nq}}\right)\right\}\\&={\frac {1}{\sqrt {2\pi npq}}}\ exp \left\{-k\ln \left({1+x{\sqrt {\frac {q}{np}}}}\right)+(kn)\ln \left({1-x{\sqrt {\frac {p}{nq}}}}\right)\right\}\qquad p+q=1\\&={\frac {1}{\sqrt {2\pi npq}}}\exp \ links\{-k\left({x{\sqrt {\frac {q}{np}}}}-{\frac {x^{2}q}{2np}}+\cdots \right)+(kn )\left({-x{\sqrt {\frac {p}{nq}}}-{\frac {x^{2}p}{2nq}}}-\cdots\right)\right\}\\ &={\frac {1}{\sqrt {2\pi npq}}}\exp \left\{\left(-np-x{\sqrt {npq}}\right)\left({x{\sqrt {\frac {q}{np}}}}-{\frac {x^{2}q}{2np}}}+\cdots \righ t)+\left(np+x{\sqrt {npq}}-n\right)\left(-x{\sqrt {\frac {p}{nq}}}-{\frac {x^{2} p}{2nq}}-\cdots\right)\right\}\\&={\frac {1}{\sqrt {2\pi npq}}}\exp \left\{\left(-np-x {\sqrt {npq}}\right)\left(x{\sqrt {\frac {q}{np}}}-{\frac {x^{2}q}{2np}}+\cdots \right) -\left(nq-x{\sqrt {npq}}\right)\left(-x{\sqrt {\frac {p}{nq}}}-{\frac {x^{2}p}{2nq }}-\cdots \right)\right\}\\&={\frac {1}{\sqrt {2\pi npq}}}\exp \left\{\left(-x{\sqrt {npq} }+{\frac {1}{2}}x^{2}qx^{2}q+\cdots \right)+\left(x{\sqrt {npq}}+{\frac {1}{2} }x^{2}px^{2}p-\cdots\right)\right\}\\&={\frac {1}{\sqrt {2\pi npq}}}\exp \left\{- {\frac {1}{2}}x^{2}q-{\frac {1}{2}}x^{2}p-\cdots \right\}\\&={\frac {1} {\sqrt {2\pi npq}}}\exp \left\{-{\frac {1}{2}}x^{2}(p+q)-\cdots \right\}\\&\simeq {\frac {1}{\sqrt {2\pi npq}}}\exp \left\{-{\frac {1}{2}}x^{2}\right\}\\&={\frac {1}{\sqrt {2\pi npq}}}e^{\frac {-(k-np)^{2}}{2npq}}\\\end{ausgerichtet}}}$

Jedes " " im obigen Argument ist eine Aussage, dass zwei Größen mit zunehmendem n asymptotisch äquivalent sind , im gleichen Sinne wie in der ursprünglichen Aussage des Satzes, dh dass das Verhältnis jedes Paars von Mengen gegen 1 geht, wenn n → ∞. ${\displaystyle \simeq}$

Wissenswertes

• Die Mauer ist ein Beispiel einer Fernsehspielshow , die den Satz von Moivre-Laplace verwendet.

Siehe auch

• Die Poisson-Verteilung ist eine alternative Näherung der Binomialverteilung für große Werte von n .

Anmerkungen