Diskrete Hartley-Transformation - Discrete Hartley transform
Eine diskrete Hartley-Transformation (DHT) ist eine Fourier-bezogene Transformation von diskreten, periodischen Daten ähnlich der diskreten Fourier-Transformation (DFT), mit analogen Anwendungen in der Signalverarbeitung und verwandten Gebieten. Der Hauptunterschied zur DFT besteht darin, dass sie reelle Eingaben in reelle Ausgaben umwandelt, ohne dass komplexe Zahlen intrinsisch beteiligt sind . So wie die DFT das diskrete Analogon der kontinuierlichen Fourier-Transformation (FT) ist, ist die DHT das diskrete Analogon der kontinuierlichen Hartley-Transformation (HT), die 1942 von Ralph VL Hartley eingeführt wurde.
Da es analoge schnelle Algorithmen für die DHT gibt, analog zur schnellen Fourier-Transformation (FFT), wurde die DHT ursprünglich 1983 von Ronald N. Bracewell als effizienteres Rechenwerkzeug für den allgemeinen Fall vorgeschlagen, in dem die Daten rein real sind. Später wurde jedoch argumentiert, dass spezialisierte FFT-Algorithmen für reale Eingaben oder Ausgaben normalerweise mit etwas weniger Operationen gefunden werden können als jeder entsprechende Algorithmus für die DHT.
Definition
Formal ist die diskrete Hartley-Transformation eine lineare, invertierbare Funktion H : R n → R n (wobei R die Menge der reellen Zahlen bezeichnet ). Die N reellen Zahlen x 0 , ..., x N −1 werden nach der Formel in die N reellen Zahlen H 0 , ..., H N −1 umgewandelt
Die Kombination wird manchmal als cas( z ) bezeichnet und sollte nicht mit cis( z ) = e iz = cos( z ) + i sin( z ) oder e − iz = cis(− z ) verwechselt werden, die in der DFT vorkommt Definition (wobei i die imaginäre Einheit ist ).
Wie bei der DFT sind der Gesamtskalenfaktor vor der Transformation und das Vorzeichen des Sinusterms Konventionssache. Obwohl diese Konventionen gelegentlich von Autor zu Autor variieren, haben sie keinen Einfluss auf die wesentlichen Eigenschaften der Transformation.
Eigenschaften
Die Transformation kann als Multiplikation des Vektors ( x 0 , ...., x N −1 ) mit einer N- mal- N- Matrix interpretiert werden ; daher ist die diskrete Hartley-Transformation ein linearer Operator . Die Matrix ist invertierbar; die inverse Transformation, die es ermöglicht, x n aus H k zurückzugewinnen , ist einfach die DHT von H k multipliziert mit 1/ N . Das heißt, das DHT ist bis auf einen Gesamtskalierungsfaktor seine eigene Umkehrung ( involutorisch ).
Die DHT kann verwendet werden, um die DFT zu berechnen und umgekehrt. Für reelle Eingaben x n hat die DFT-Ausgabe X k einen Realteil ( H k + H N – k )/2 und einen Imaginärteil ( H N – k – H k )/2. Umgekehrt entspricht die DHT der Berechnung der DFT von x n multipliziert mit 1 + i , wobei dann der Realteil des Ergebnisses genommen wird.
Wie bei der DFT wird eine zyklische Faltung z = x ∗ y zweier Vektoren x = ( x n ) und y = ( y n ), um einen Vektor z = ( z n ) der Länge N zu erzeugen , zu einer einfachen Operation nach die DHT. Nehmen wir insbesondere an, dass die Vektoren X , Y und Z die DHT von x , y bzw. z bezeichnen. Dann sind die Elemente von Z gegeben durch:
wobei wir alle Vektoren als periodisch in N annehmen ( X N = X 0 , usw.). So wie die DFT eine Faltung in eine punktweise Multiplikation komplexer Zahlen ( Paare von Real- und Imaginärteilen) umwandelt, transformiert die DHT eine Faltung in eine einfache Kombination von Paaren reeller Frequenzkomponenten. Die inverse DHT liefert dann den gewünschten Vektor z . Auf diese Weise ergibt ein schneller Algorithmus für das DHT (siehe unten) einen schnellen Algorithmus für die Faltung. (Dies ist etwas teurer als das entsprechende Verfahren für die DFT, ohne die Kosten der nachfolgenden Transformationen, da die obige paarweise Operation 8 reelle arithmetische Operationen im Vergleich zu den 6 einer komplexen Multiplikation erfordert. Diese Zählung beinhaltet nicht die Division durch 2, die zB in die 1/ N- Normalisierung des inversen DHT aufgenommen werden kann.)
Schnelle Algorithmen
Ebenso wie für die DFT, direkt die DHT Definition Auswertung erfordern würde O ( N 2 ) arithmetische Operationen (siehe Big O - Notation ). Es gibt jedoch schnelle Algorithmen ähnlich der FFT, die das gleiche Ergebnis nur in O( N log N ) Operationen berechnen . Fast jeder FFT-Algorithmus, von Cooley-Tukey über Primfaktor bis Winograd (1985) bis Bruuns (1993), hat ein direktes Analogon für die diskrete Hartley-Transformation. (Allerdings wurden einige der exotischeren FFT-Algorithmen, wie die QFT, noch nicht im Zusammenhang mit der DHT untersucht.)
Insbesondere wird der DHT - Analogon des Cooley-Tukey - Algorithmus , wie die allgemein bekannte schnelle Hartley - Transformation (FHT) Algorithmus und wurde zuerst von Bracewell in 1984. Diesen FHT - Algorithmus beschrieben wird , zumindest , wenn sie angewandt Potenz von zwei Größen N , ist Gegenstand des US- Patents Nr. 4,646,256, das 1987 an die Stanford University erteilt wurde . Stanford hat dieses Patent 1994 gemeinfrei gemacht (Bracewell, 1995).
Wie oben erwähnt, sind DHT-Algorithmen typischerweise etwas weniger effizient (in Bezug auf die Anzahl von Gleitkommaoperationen ) als der entsprechende DFT-Algorithmus (FFT), der auf reale Eingaben (oder Ausgaben) spezialisiert ist. Dies wurde erstmals von Sorensen et al. (1987) und Duhamel & Vetterli (1987). Die letztgenannten Autoren erhielten die scheinbar niedrigste veröffentlichte Operationszahl für die DHT mit Zweierpotenzgrößen, indem sie einen Split-Radix-Algorithmus (ähnlich der Split-Radix-FFT ) verwendeten, der eine DHT der Länge N in eine DHT von . zerlegt Länge N /2 und zwei Real-Input-DFTs ( keine DHTs) der Länge N /4. Auf diese Weise argumentierten sie, dass eine DHT mit einer Zweierpotenz-Länge bestenfalls mit 2 Additionen mehr berechnet werden kann als die entsprechende Anzahl von arithmetischen Operationen für die Real-Input-DFT.
Auf modernen Computern wird die Leistung mehr durch Überlegungen zum Cache und zur CPU-Pipeline bestimmt als durch strikte Betriebszählungen, und ein geringfügiger Unterschied bei den arithmetischen Kosten ist unwahrscheinlich. Da FHT- und Real-Input-FFT-Algorithmen ähnliche Rechenstrukturen aufweisen, scheint keiner von beiden einen wesentlichen Geschwindigkeitsvorteil a priori zu haben ( Popović und Šević, 1994). Aus praktischen Gründen sind hochoptimierte Real-Input-FFT-Bibliotheken von vielen Quellen erhältlich (zB von CPU-Herstellern wie Intel ), während hochoptimierte DHT-Bibliotheken weniger verbreitet sind.
Andererseits sind die redundanten Berechnungen in FFTs aufgrund von reellen Eingaben für große Primzahlen N schwieriger zu eliminieren , trotz der Existenz von O( N log N ) komplexen Datenalgorithmen für solche Fälle, da die Redundanzen hinter komplizierten Permutationen verborgen sind und/oder Phasendrehungen in diesen Algorithmen. Im Gegensatz dazu kann ein Standard-Prime-Size-FFT-Algorithmus, der Rader-Algorithmus , direkt auf die DHT von realen Daten angewendet werden, was ungefähr einen Faktor von zwei weniger Rechenaufwand erfordert als der der äquivalenten komplexen FFT (Frigo und Johnson, 2005). Andererseits ist auch eine nicht-DHT-basierte Anpassung des Rader-Algorithmus für Real-Input-DFTs möglich (Chu & Burrus , 1982).
Mehrdimensionale diskrete Hartley-Transformation (MD-DHT)
Der rD-DHT (MD-DHT mit "r"-Abmessungen) ist gegeben durch
mit und wo
Ähnlich dem 1-D-Fall ist die MD-DHT als reelle und symmetrische Transformation einfacher als die MD-DFT. Zum einen ist die inverse DHT identisch mit der Vorwärtstransformation, mit der Hinzufügung eines Skalierungsfaktors;
und zweitens vermeidet er, da der Kernel reell ist, die Rechenkomplexität komplexer Zahlen . Außerdem ist die DFT durch eine einfache additive Operation direkt aus der DHT erhältlich (Bracewell, 1983).
Der MD-DHT wird häufig in Bereichen wie der Bild- und optischen Signalverarbeitung eingesetzt. Spezifische Anwendungen umfassen Computer Vision, hochauflösendes Fernsehen und Telekonferenzen, Bereiche, die bewegte Bilder verarbeiten oder analysieren (Zeng, 2000).
Schnelle Algorithmen für das MD-DHT
Da die Rechengeschwindigkeit weiter zunimmt, werden größere mehrdimensionale Probleme rechnerisch durchführbar, was die Notwendigkeit schneller mehrdimensionaler Algorithmen erfordert. Es folgen drei solcher Algorithmen.
Im Streben nach Trennbarkeit für Effizienz betrachten wir die folgende Transformation (Bracewell, 1983):
In Bortfeld (1995) wurde gezeigt, dass die beiden durch einige Ergänzungen in Beziehung gesetzt werden können. Zum Beispiel in 3D,
Für können dann Zeilen-Spalten-Algorithmen implementiert werden. Diese Technik wird aufgrund der Einfachheit solcher RC-Algorithmen häufig verwendet, aber sie sind nicht für allgemeine MD-Räume optimiert.
Andere schnelle Algorithmen wurden entwickelt, wie Radix-2, Radix-4 und Split-Radix. Boussakta (2000) entwickelte beispielsweise die 3D-Vektor-Radix,
In Boussakta (2000) wurde auch präsentiert, dass dieser 3D-Vektor-Radix-Algorithmus Multiplikationen und Additionen im Vergleich zu Multiplikationen und Additionen aus dem Zeilen-Spalten-Ansatz nimmt. Der Nachteil besteht darin, dass die Implementierung dieser Algorithmen vom Radix-Typ für Signale beliebiger Dimensionen schwer zu verallgemeinern ist.
Zahlentheoretische Transformationen wurden auch zum Lösen des MD-DHT verwendet, da sie extrem schnelle Faltungen durchführen. In Boussakta (1988) wurde gezeigt, wie man die MD-DHT-Transformation in eine aus Faltungen bestehende Form zerlegt:
Für den 2-D-Fall (der 3-D-Fall wird auch in der angegebenen Referenz behandelt),
,
lässt sich wie folgt in 1-D- und 2-D-Kreisfaltungen zerlegen:
wo
Die Entwicklung weiterer,
An dieser Stelle stellen wir die Fermat-Zahlentransformation (FNT) vor. Die t- te Fermat-Zahl ist gegeben durch , mit . Die bekannten Fermat-Zahlen sind für ( ist eine Primzahl für ), (Boussakta, 1988). Die Fermat-Zahlentransformation ist gegeben durch
mit . und sind Wurzeln der Einheit der Ordnung und jeweils .
Zurück zur Zerlegung, der letzte Term für wird als bezeichnet , dann
Wenn und sind primitive Wurzeln von und (die garantiert werden , bestehen , wenn und sind prime ) dann und Karte zu So, Kartierung und zu und erhält man die folgende,
.
Was jetzt eine kreisförmige Faltung ist . Mit , , und hat man
wobei bezeichnet Term-für-Term-Multiplikation. In (Boussakta, 1988) wurde auch festgestellt, dass dieser Algorithmus die Anzahl der Multiplikationen gegenüber anderen DHT-Algorithmen um den Faktor 8–20 reduziert, auf Kosten einer leichten Erhöhung der Anzahl der Verschiebungs- und Additionsoperationen, von denen angenommen wird, dass sie einfacher als Multiplikationen. Der Nachteil dieses Algorithmus ist die Einschränkung, dass jede Dimension der Transformation eine primitive Wurzel hat .
Verweise
Weiterlesen
- Bracewell, Ronald N. (1986). Die Hartley-Transformation (1 Hrsg.). Oxford University Press . ISBN 978-0-19503969-6.
- Boussakta, Said; Holt, Alan GJ (1988). „Schnelle mehrdimensionale diskrete Hartley-Transformation mit Fermat-Zahlentransformation“. IEE Proceedings G - Elektronische Schaltungen und Systeme . 135 (6): 235–237. doi : 10.1049/ip-g-1.1988.0036 .
- Hong, Jonathan; Vetterli, Martin ; Duhamel, Pierre (1994). "Basisfeld transformiert mit der Faltungseigenschaft" (PDF) . Verfahren der IEEE . 82 (3): 400–412. doi : 10.1109/5.272145 .
- O'Neill, Mark A. (1988). "Schneller als Fast Fourier". BYTE . 13 (4): 293–300.
- Olnejniczak, Kraig J.; Heydt, Gerald T. (März 1994). „Scannen des speziellen Abschnitts über die Hartley-Transformation“. Verfahren der IEEE . 82 : 372–380. (NB. Enthält umfangreiche Bibliographie.)

![{\displaystyle H_{k}=\sum _{n=0}^{N-1}x_{n}\operatorname {cas} \left({\frac {2\pi }{N}}nk\right) =\sum _{n=0}^{N-1}x_{n}\left[\cos\left({\frac {2\pi }{N}}nk\right)+\sin\left({ \frac{2\pi}{N}}nk\right)\right]\quad \quad k=0,\dots,N-1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73ba8d036230283b86eb38c9e498e214973d0a0d)


![{\begin{matrix}Z_{k}&=&\left[X_{k}\left(Y_{k}+Y_{{Nk}}\right)+X_{{Nk}}\left(Y_{k }-Y_{{Nk}}\right)\right]/2\\Z_{{Nk}}&=&\left[X_{{Nk}}\left(Y_{k}+Y_{{Nk}} \right)-X_{k}\left(Y_{k}-Y_{{Nk}}\right)\right]/2\end{matrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4fae2de8d1caaf64f2b6e5e1a877133bebe6a39)



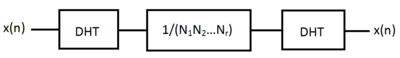

![{\displaystyle X(k_{1},k_{2},k_{3})={\frac {1}{2}}[{\hat {X}}(k_{1},k_{2}, -k_{3})+{\hat{X}}(k_{1},-k_{2},k_{3})+{\hat{X}}(-k_{1},k_{2} ,k_{3})-{\hat{X}}(-k_{1},-k_{2},-k_{3})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7357fed5235398b385ba6cb3b68e9a073e5704)




















































![{\displaystyle Y(k,l)=FNT^{-1}\{FNT[y(n,m)]\otimes FNT[h(n,m)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eebe41901610887e540c58bc1d96b810eb607165)
