Einstein fest - Einstein solid

Statistische Mechanik
Thermodynamik Kinetische Theorie
Partikelstatistik Spin-Statistik-Theorem Identische Partikel Maxwell-Boltzmann Bose-Einstein Fermi-Dirac Parastatistik Anyonic Statistik Geflechtstatistik
Thermodynamische Ensembles NVE Microcanonical NVT Canonical µVT Grand Canonical NPH Isoenthalpic-Isobaric NPT Isothermisch-Isobar
Modelle Debye Einstein Ich singe Potts
Potenziale Innere Energie Enthalpie Helmholtz freie Energie Gibbs freie Energie Großes Potenzial / Landau freie Energie
Wissenschaftler Maxwell Boltzmann Gibbs Einstein Ehrenfest von Neumann Tolman Debye Fermi Bose
v t e

Der Einstein-Festkörper ist ein Modell eines kristallinen Festkörpers, der eine große Anzahl unabhängiger dreidimensionaler Quantenharmonischer Oszillatoren derselben Frequenz enthält. Die Unabhängigkeitsannahme wird im Debye-Modell gelockert .

Während das Modell eine qualitative Übereinstimmung mit experimentellen Daten liefert, insbesondere für die Hochtemperaturgrenze, sind diese Schwingungen tatsächlich Phononen oder kollektive Moden, an denen viele Atome beteiligt sind. Einstein war sich bewusst, dass es schwierig sein würde, die Frequenz der tatsächlichen Schwingungen zu ermitteln, schlug diese Theorie jedoch vor, da dies ein besonders klarer Beweis dafür war, dass die Quantenmechanik das spezifische Wärmeproblem in der klassischen Mechanik lösen kann.

Historische Auswirkungen

Die ursprüngliche Theorie, die Einstein 1907 vorschlug, hat große historische Relevanz. Die nach dem empirischen Dulong-Petit-Gesetz vorhergesagte Wärmekapazität von Festkörpern wurde von der klassischen Mechanik gefordert . Die spezifische Wärme von Festkörpern sollte unabhängig von der Temperatur sein. Experimente bei niedrigen Temperaturen zeigten jedoch, dass sich die Wärmekapazität ändert und beim absoluten Nullpunkt auf Null geht. Mit steigender Temperatur steigt die spezifische Wärme, bis sie sich bei hohen Temperaturen der Dulong- und Petit-Vorhersage nähert.

Unter Verwendung der Planckschen Quantisierungsannahme berücksichtigte Einsteins Theorie erstmals den beobachteten experimentellen Trend. Zusammen mit dem photoelektrischen Effekt wurde dies zu einem der wichtigsten Beweise für die Notwendigkeit einer Quantisierung. Einstein benutzte die Pegel des quantenmechanischen Oszillators viele Jahre vor dem Aufkommen der modernen Quantenmechanik .

Wärmekapazität

Für einen thermodynamischen Ansatz kann die Wärmekapazität unter Verwendung verschiedener statistischer Ensembles abgeleitet werden . Alle Lösungen sind an der thermodynamischen Grenze gleichwertig .

Mikrokanonisches Ensemble

Wärmekapazität eines Einstein-Feststoffs als Funktion der Temperatur. Der experimentelle Wert von 3 Nk wird bei hohen Temperaturen gewonnen.

Die Wärmekapazität eines Objekts bei konstantem Volumen V wird durch die innere Energie U als definiert

${\ displaystyle C_ {V} = \ left ({\ partielles U \ über \ partielles T} \ rechts) _ {V}.}$

${\ displaystyle T}$ Die Temperatur des Systems ergibt sich aus der Entropie

${\ displaystyle {1 \ over T} = {\ partielles S \ über \ partielles U}.}$

Um die Entropie zu finden, betrachten Sie einen Feststoff aus Atomen, von denen jeder 3 Freiheitsgrade hat. Es gibt also quantenharmonische Oszillatoren (im Folgenden SHOs für "Simple Harmonic Oscillators"). ${\ displaystyle N}$${\ displaystyle 3N}$

${\ displaystyle N ^ {\ prime} = 3N}$

Mögliche Energien eines SHO sind gegeben durch

${\ displaystyle E_ {n} = \ hbar \ omega \ left (n + {1 \ over 2} \ right)}$

oder, mit anderen Worten, die Energieniveaus gleichmäßig beabstandet und man kann eine Definition Quantenenergie

${\ displaystyle \ varepsilon = \ hbar \ omega}$

Dies ist der kleinste und einzige Betrag, um den die Energie eines SHO erhöht wird. Als nächstes müssen wir die Vielzahl des Systems berechnen. Berechnen Sie also die Anzahl der Möglichkeiten, Energiequanten unter SHOs zu verteilen. Diese Aufgabe wird einfacher, wenn man daran denkt, Kieselsteine ​​über Kisten zu verteilen ${\ displaystyle q}$${\ displaystyle N ^ {\ prime}}$${\ displaystyle q}$${\ displaystyle N ^ {\ prime}}$

oder Trennen von Kieselstapeln mit Trennwänden ${\ displaystyle N ^ {\ prime} -1}$

oder Anordnen von Kieselsteinen und Trennwänden ${\ displaystyle q}$${\ displaystyle N ^ {\ prime} -1}$

Das letzte Bild ist das aussagekräftigste. Die Anzahl der Anordnungen von  Objekten beträgt . Die Anzahl der möglichen Anordnungen von Kieselsteinen und Trennwänden ist also . Wenn jedoch Partition 3 und Partition 5 tauschen, würde dies niemand bemerken. Das gleiche Argument gilt für Quanten. Um die Anzahl möglicher unterscheidbarer Anordnungen zu erhalten, muss man die Gesamtzahl der Anordnungen durch die Anzahl nicht unterscheidbarer Anordnungen dividieren . Es gibt identische Quantenanordnungen und identische Partitionsanordnungen. Daher ist die Vielzahl des Systems gegeben durch ${\ displaystyle n}$${\ displaystyle n!}$${\ displaystyle q}$${\ displaystyle N ^ {\ prime} -1}$${\ displaystyle \ left (q + N ^ {\ prime} -1 \ right)!}$${\ displaystyle q!}$${\ displaystyle (N ^ {\ prime} -1)!}$

${\ displaystyle \ Omega = {\ left (q + N ^ {\ prime} -1 \ right)! \ over q! (N ^ {\ prime} -1)!}}$

Dies ist, wie bereits erwähnt, die Anzahl der Möglichkeiten, Energiequanten in Oszillatoren abzuscheiden . Die Entropie des Systems hat die Form ${\ displaystyle q}$${\ displaystyle N ^ {\ prime}}$

${\ displaystyle S / k = \ ln \ Omega = \ ln {\ left (q + N ^ {\ prime} -1 \ right)! \ over q! (N ^ {\ prime} -1)!}.}$

${\ displaystyle N ^ {\ prime}}$ ist eine riesige Zahl - das Subtrahieren einer Zahl hat keinerlei Gesamteffekt:

${\ displaystyle S / k \ approx \ ln {\ left (q + N ^ {\ prime} \ right)! \ over q! N ^ {\ prime}!}}$

Mit Hilfe von Stirlings Näherung kann die Entropie vereinfacht werden:

${\ displaystyle S / k \ approx \ left (q + N ^ {\ prime} \ right) \ ln \ left (q + N ^ {\ prime} \ right) -N ^ {\ prime} \ ln N ^ { \ prime} -q \ ln q.}$

Die Gesamtenergie des Feststoffs ist gegeben durch

${\ displaystyle U = {N ^ {\ prime} \ varepsilon \ over 2} + q \ varepsilon,}$

da es im System zusätzlich zur Grundzustandsenergie jedes Oszillators insgesamt q Energiequanten gibt. Einige Autoren wie Schröder lassen diese Grundzustandsenergie in ihrer Definition der Gesamtenergie eines Einstein-Festkörpers weg.

Wir sind jetzt bereit, die Temperatur zu berechnen

${\ displaystyle {1 \ over T} = {\ partielles S \ über \ partielles U} = {\ partielles S \ über \ partielles q} {dq \ über dU} = {1 \ über \ varepsilon} {\ partielles S \ über \ partielles q} = {k \ über \ varepsilon} \ ln \ left (1 + N ^ {\ prime} / q \ right)}$

Die Eliminierung von q zwischen den beiden vorhergehenden Formeln ergibt für U:

${\ displaystyle U = {N ^ {\ prime} \ varepsilon \ over 2} + {N ^ {\ prime} \ varepsilon \ over e ^ {\ varepsilon / kT} -1}.}$

Der erste Term ist mit Nullpunktsenergie verbunden und trägt nicht zur spezifischen Wärme bei. Es geht daher im nächsten Schritt verloren.

Differenzierung in Bezug auf die zu findende Temperatur erhalten wir: ${\ displaystyle C_ {V}}$

${\ displaystyle C_ {V} = {\ partielles U \ über \ partielles T} = {N ^ {\ prime} \ varepsilon ^ {2} \ über kT ^ {2}} {e ^ {\ varepsilon / kT} \ über \ left (e ^ {\ varepsilon / kT} -1 \ right) ^ {2}}}$

oder

${\ displaystyle C_ {V} = 3Nk \ left ({\ varepsilon \ over kT} \ right) ^ {2} {e ^ {\ varepsilon / kT} \ over \ left (e ^ {\ varepsilon / kT} -1 \ right) ^ {2}}.}$

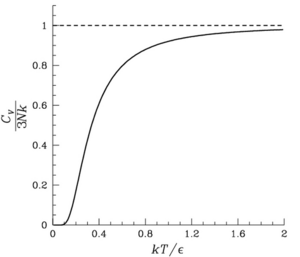
Obwohl das Einstein-Modell des Festkörpers die Wärmekapazität bei hohen Temperaturen und in dieser Grenze genau vorhersagt

${\ displaystyle \ lim _ {T \ rightarrow \ infty} C_ {V} = 3Nk}$ ,

Dies entspricht dem Dulong-Petit-Gesetz .

Trotzdem weicht die Wärmekapazität bei niedrigen Temperaturen deutlich von den experimentellen Werten ab. Informationen zur Berechnung genauer Wärmekapazitäten bei niedrigen Temperaturen finden Sie im Debye-Modell .

Kanonisches Ensemble

Die Wärmekapazität wird durch die Verwendung der kanonischen Partitionsfunktion eines einfachen Quantenharmonischen Oszillators erhalten.

${\ displaystyle Z = \ sum _ {n = 0} ^ {\ infty} e ^ {- E_ {n} / kT}}$

wo

${\ displaystyle E_ {n} = \ varepsilon \ left (n + {1 \ over 2} \ right)}$

Einsetzen in die Partitionsfunktionsformel ergibt

${\ displaystyle {\ begin {align} Z = \ sum _ {n = 0} ^ {\ infty} e ^ {- \ varepsilon \ left (n + 1/2 \ right) / kT} = e ^ {- \ varepsilon / 2kT} \ sum _ {n = 0} ^ {\ infty} e ^ {- n \ varepsilon / kT} = e ^ {- \ varepsilon / 2kT} \ sum _ {n = 0} ^ {\ infty} \ left (e ^ {- \ varepsilon / kT} \ right) ^ {n} \\ = {e ^ {- \ varepsilon / 2kT} \ over 1-e ^ {- \ varepsilon / kT}} = {1 \ über e ^ {\ varepsilon / 2kT} -e ^ {- \ varepsilon / 2kT}} = {1 \ über 2 \ sinh \ left ({\ varepsilon \ over 2kT} \ right)}. \ end {align}}}$

Dies ist die Partitionsfunktion eines harmonischen Oszillators. Da statistisch gesehen Wärmekapazität, Energie und Entropie des Festkörpers gleichmäßig auf seine Atome verteilt sind, können wir mit dieser Verteilungsfunktion arbeiten, um diese Größen zu erhalten, und sie dann einfach mit multiplizieren , um die Summe zu erhalten. Als nächstes berechnen wir die durchschnittliche Energie jedes Oszillators ${\ displaystyle N ^ {\ prime}}$

${\ displaystyle \ langle E \ rangle = U = - {1 \ über Z} \ teilweise _ {\ beta} Z}$

wo

${\ displaystyle \ beta = {1 \ over kT}.}$

Deshalb,

${\ displaystyle U = -2 \ sinh \ left ({\ varepsilon \ over 2kT} \ right) {- \ cosh \ left ({\ varepsilon \ over 2kT} \ right) \ over 2 \ sinh ^ {2} \ left ({\ varepsilon \ over 2kT} \ right)} {\ varepsilon \ over 2} = {\ varepsilon \ over 2} \ coth \ left ({\ varepsilon \ over 2kT} \ right).}$

Die Wärmekapazität eines Oszillators beträgt dann

${\ displaystyle c_ {V} = {\ partielles U \ über \ partielles T} = - {\ varepsilon \ über 2} {1 \ über \ sinh ^ {2} \ left ({\ varepsilon \ over 2kT} \ right) } \ left (- {\ varepsilon \ over 2kT ^ {2}} \ right) = k \ left ({\ varepsilon \ over 2kT} \ right) ^ {2} {1 \ over \ sinh ^ {2} \ left ({\ varepsilon \ over 2kT} \ right)}.}$

Bisher haben wir die Wärmekapazität eines einzigartigen Freiheitsgrades berechnet, der als Quantenharmonische modelliert wurde. Die Wärmekapazität des gesamten Festkörpers ergibt sich dann aus der Gesamtzahl der Atome im Festkörper , wobei die Gesamtzahl der Freiheitsgrade des Festkörpers das Dreifache (für die drei gerichteten Freiheitsgrade) beträgt. Man erhält also ${\ displaystyle C_ {V} = 3Nc_ {V}}$${\ displaystyle N}$

${\ displaystyle C_ {V} = 3Nk \ left ({\ varepsilon \ over 2kT} \ right) ^ {2} {1 \ over \ sinh ^ {2} \ left ({\ varepsilon \ over 2kT} \ right)} .}$

Dies ist algebraisch identisch mit der im vorherigen Abschnitt abgeleiteten Formel.

Die Menge hat die Dimensionen der Temperatur und ist eine charakteristische Eigenschaft eines Kristalls. Es ist als Einstein-Temperatur bekannt . Das Einstein-Kristallmodell sagt daher voraus, dass die Energie- und Wärmekapazitäten eines Kristalls universelle Funktionen des dimensionslosen Verhältnisses sind . In ähnlicher Weise sagt das Debye-Modell eine universelle Funktion des Verhältnisses voraus , wobei die Debye-Temperatur ist. ${\ displaystyle T _ {\ rm {E}} = \ varepsilon / k}$${\ displaystyle T / T _ {\ rm {E}}}$${\ displaystyle T / T _ {\ rm {D}}}$${\ displaystyle T _ {\ rm {D}}}$

Einschränkungen und Erfolgsmodell

In Einsteins Modell nähert sich die spezifische Wärme bei niedrigen Temperaturen exponentiell schnell Null. Dies liegt daran, dass alle Schwingungen eine gemeinsame Frequenz haben. Das richtige Verhalten wird gefunden, indem die normalen Moden des Festkörpers auf die von Einstein vorgeschlagene Weise quantisiert werden . Dann sind die Frequenzen der Wellen nicht alle gleich, und die spezifische Wärme geht als Potenzgesetz, das dem Experiment entspricht, auf Null . Diese Modifikation wird als Debye-Modell bezeichnet , das 1912 erschien. ${\ displaystyle T ^ {3}}$

Als Walther Nernst von Einsteins Artikel über spezifische Hitze von 1906 erfuhr, war er so aufgeregt, dass er den ganzen Weg von Berlin nach Zürich reiste, um sich mit ihm zu treffen.

Siehe auch

• Kinetische Festkörpertheorie

Verweise

Externe Links

• Zeleny, Enrique. "Das Wolfram-Demonstrationsprojekt - Einstein Solid" . Abgerufen am 18.03.2016 . .