Gradientenabstieg - Gradient descent

Medien abspielen

Gradientenabstieg in 2D

Gradientenabfallsaktualisierung ist eine erste Ordnung iterative Optimierung Algorithmus ein für die Suche nach lokalen Minimum einer differenzierbare Funktion . Die Idee ist, wiederholte Schritte in die entgegengesetzte Richtung des Gradienten (oder ungefähren Gradienten) der Funktion am aktuellen Punkt zu machen, da dies die Richtung des steilsten Abstiegs ist. Umgekehrt führt ein Schritt in Richtung des Gradienten zu einem lokalen Maximum dieser Funktion; der Vorgang wird dann als Gefälleaufstieg bezeichnet .

Der Gradientenabstieg wird im Allgemeinen Cauchy zugeschrieben , der sie erstmals 1847 vorschlug. Hadamard schlug 1907 unabhängig eine ähnliche Methode vor. Seine Konvergenzeigenschaften für nichtlineare Optimierungsprobleme wurden erstmals 1944 von Haskell Curry untersucht , wobei die Methode immer besser untersucht wurde und in den folgenden Jahrzehnten verwendet, oft auch als steilste Abfahrt bezeichnet.

Beschreibung

Illustration des Gradientenabstiegs auf einer Reihe von Level-Sets

Gradientenabstieg liegt die Beobachtung zugrunde , dass , wenn die multivariable Funktion ist definiert und differenzierbar in einer Nachbarschaft eines Punktes , dann verringert sich am schnellsten , wenn man aus geht in Richtung des negativen Gradienten der an . Daraus folgt, wenn ${\displaystyle F(\mathbf{x})}$${\displaystyle\mathbf{a}}$${\displaystyle F(\mathbf{x})}$${\displaystyle\mathbf{a}}$${\displaystyle F}$${\displaystyle\mathbf{a},-\nabla F(\mathbf{a})}$

${\displaystyle\mathbf{a}_{n+1}=\mathbf{a}_{n}-\gamma\nabla F(\mathbf{a}_{n})}$

für eine kleine genug, dann . Mit anderen Worten, der Term wird abgezogen, weil wir uns gegen den Gradienten zum lokalen Minimum bewegen wollen. Mit dieser Beobachtung im Hinterkopf beginnt man mit einer Schätzung für ein lokales Minimum von und betrachtet die Folge so, dass ${\displaystyle\gamma\in\mathbb{R}_{+}}$${\displaystyle F(\mathbf {a_{n}} )\geq F(\mathbf {a_{n+1}} )}$${\displaystyle \gamma\nabla F(\mathbf{a})}$${\displaystyle\mathbf{a}}$${\displaystyle \mathbf {x} _{0}}$${\displaystyle F}$${\displaystyle \mathbf{x}_{0},\mathbf{x}_{1},\mathbf{x}_{2},\ldots}$

${\displaystyle \mathbf{x}_{n+1}=\mathbf{x}_{n}-\gamma_{n}\nabla F(\mathbf{x}_{n}),\n\geq 0.}$

Wir haben eine monotone Folge

${\displaystyle F(\mathbf{x}_{0})\geq F(\mathbf{x}_{1})\geq F(\mathbf{x}_{2})\geq\cdots,}$

die Folge konvergiert also hoffentlich gegen das gewünschte lokale Minimum. Beachten Sie, dass sich der Wert der Schrittweite bei jeder Iteration ändern darf. Mit bestimmten Annahmen über die Funktion (z. B. konvex und Lipschitz ) und bestimmten Wahlmöglichkeiten von (z. B. ausgewählt entweder über eine Liniensuche , die die Wolfe-Bedingungen erfüllt , oder die Barzilai-Borwein-Methode wie folgt gezeigt), ${\displaystyle (\mathbf{x}_{n})}$ ${\displaystyle\gamma}$${\displaystyle F}$${\displaystyle F}$ ${\displaystyle \nabla F}$ ${\displaystyle\gamma}$

${\displaystyle \gamma_{n}={\frac {\left|\left(\mathbf{x}_{n}-\mathbf{x}_{n-1}\right)^{T}\left [\nabla F(\mathbf{x}_{n})-\nabla F(\mathbf{x}_{n-1})\right]\right|}{\left\|\nabla F(\mathbf {x}_{n})-\nabla F(\mathbf{x}_{n-1})\right\|^{2}}}}$

Konvergenz zu einem lokalen Minimum kann garantiert werden. Wenn die Funktion ist konvex , sind alle lokalen Minima auch globalen Minima, also in diesem Fall Gradientenabfallsaktualisierung zur globalen Lösung konvergieren kann. ${\displaystyle F}$

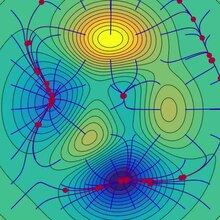
Dieser Vorgang ist im nebenstehenden Bild dargestellt. Hier wird angenommen, dass sie auf der Ebene definiert ist und dass ihr Graph eine Schüsselform hat. Die blauen Kurven sind die Höhenlinien , dh die Bereiche, in denen der Wert von konstant ist. Ein roter Pfeil, der von einem Punkt ausgeht, zeigt die Richtung des negativen Gradienten an diesem Punkt an. Beachten Sie, dass der (negative) Gradient an einem Punkt orthogonal zu der durch diesen Punkt verlaufenden Höhenlinie verläuft. Wir sehen , dass Gradienten Abstieg führt uns auf den Boden der Schüssel, die bis zu dem Punkt, wo der Wert der Funktion minimal ist. ${\displaystyle F}$${\displaystyle F}$${\displaystyle F}$

Eine Analogie zum Verständnis des Gradientenabstiegs

Nebel in den Bergen

Die grundlegende Intuition hinter dem Gradientenabstieg kann durch ein hypothetisches Szenario veranschaulicht werden. Eine Person steckt in den Bergen fest und versucht hinunterzukommen (dh versucht, das globale Minimum zu finden). Es herrscht starker Nebel, so dass die Sicht extrem gering ist. Daher ist der Weg den Berg hinunter nicht sichtbar, daher müssen sie lokale Informationen verwenden, um das Minimum zu finden. Sie können die Methode des Gradientenabstiegs verwenden, bei der die Steilheit des Hügels an ihrer aktuellen Position betrachtet und dann in die Richtung mit der steilsten Abfahrt (dh bergab) vorgegangen wird. Wenn sie den Gipfel des Berges (dh das Maximum) finden wollten, würden sie in Richtung des steilsten Aufstiegs (dh bergauf) vorgehen. Mit dieser Methode würden sie schließlich ihren Weg den Berg hinunter finden oder möglicherweise in einem Loch (dh einem lokalen Minimum oder einem Sattelpunkt ) wie einem Bergsee stecken bleiben . Nehmen Sie jedoch auch an, dass die Steilheit des Hügels bei einfacher Beobachtung nicht sofort ersichtlich ist, sondern ein ausgeklügeltes Messinstrument erforderlich ist, das die Person im Moment zufällig besitzt. Es dauert einige Zeit, die Steilheit des Hügels mit dem Instrument zu messen, daher sollten sie den Gebrauch des Instruments minimieren, wenn sie den Berg vor Sonnenuntergang hinunterfahren möchten. Die Schwierigkeit besteht dann darin, die Häufigkeit zu wählen, mit der die Steilheit des Hügels gemessen werden soll, um nicht von der Spur abzuweichen.

In dieser Analogie repräsentiert die Person den Algorithmus, und der Weg, den man den Berg hinunter nimmt, repräsentiert die Abfolge von Parametereinstellungen, die der Algorithmus untersuchen wird. Die Steilheit des Hügels repräsentiert die Steigung der Fehlerfläche an diesem Punkt. Das zur Messung der Steilheit verwendete Instrument ist die Differentiation (die Steigung der Fehlerfläche kann berechnet werden, indem die Ableitung der quadratischen Fehlerfunktion an diesem Punkt gebildet wird). Die Richtung, in der sie sich bewegen, richtet sich nach dem Gradienten der Fehleroberfläche an diesem Punkt. Die Zeit, die sie zurücklegen, bevor eine weitere Messung durchgeführt wird, ist die Schrittgröße.

Beispiele

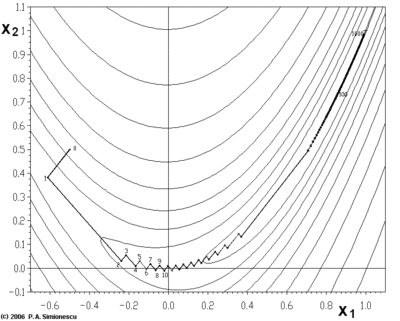
Der Gradientenabstieg hat Probleme mit pathologischen Funktionen wie der hier gezeigten Rosenbrock-Funktion .

${\displaystyle f(x_{1},x_{2})=(1-x_{1})^{2}+100(x_{2}-x_{1}^{2})^{2}. }$

Die Rosenbrock-Funktion hat ein schmales geschwungenes Tal, das das Minimum enthält. Die Talsohle ist sehr flach. Aufgrund des gekrümmten flachen Tals geht die Optimierung im Zickzack langsam mit kleinen Schrittweiten zum Minimum hin. Der Whiplash Gradient Descent löst dieses Problem insbesondere.

Die Zickzack-Natur der Methode wird auch unten deutlich, wo die Gradientenabstiegsmethode angewendet wird auf

${\displaystyle F(x,y)=\sin\left({\frac {1}{2}}x^{2}-{\frac {1}{4}}y^{2}+3\right )\cos\left(2x+1-e^{y}\right).}$

Schrittgröße und Abstiegsrichtung wählen

Da die Verwendung einer zu kleinen Schrittweite die Konvergenz verlangsamen würde und eine zu große zu einer Divergenz führen würde, ist das Auffinden einer guten Einstellung von ein wichtiges praktisches Problem. Philip Wolfe sprach sich auch dafür aus, "kluge Entscheidungen der [Abstiegs-]Richtung" in der Praxis zu verwenden. Während die Verwendung einer Richtung, die von der steilsten Abstiegsrichtung abweicht, kontraintuitiv erscheinen mag, besteht die Idee darin, dass die kleinere Steigung dadurch ausgeglichen werden kann, dass sie über eine viel längere Distanz aufrechterhalten wird. ${\displaystyle\gamma}$${\displaystyle\gamma}$${\displaystyle\gamma}$

Um dies mathematisch zu begründen, verwenden wir eine Richtung und Schrittweite und betrachten das allgemeinere Update: ${\displaystyle \mathbf {p} _{n}}$${\displaystyle \gamma_{n}}$

${\displaystyle \mathbf{a}_{n+1}=\mathbf{a}_{n}-\gamma_{n}\,\mathbf{p}_{n}}$.

Das Finden guter Einstellungen von und erfordert ein wenig Nachdenken. Zunächst möchten wir, dass die Update-Richtung bergab zeigt. Mathematisch den Winkel zwischen und bezeichnen zu lassen , erfordert dies: Um mehr zu sagen, benötigen wir mehr Informationen über die Zielfunktion, die wir optimieren. Unter der ziemlich schwachen Annahme, die stetig differenzierbar ist, können wir beweisen, dass: ${\displaystyle \mathbf {p} _{n}}$${\displaystyle \gamma_{n}}$${\displaystyle \theta_{n}}$${\displaystyle \nabla F(\mathbf{a_{n}} )}$${\displaystyle \mathbf {p} _{n}}$${\displaystyle \cos\theta_{n}>0.}$${\displaystyle F}$

${\displaystyle F(\mathbf{a}_{n+1})\leq F(\mathbf{a}_{n})-\gamma_{n}\|\nabla F(\mathbf{a}_ {n})\|_{2}\|\mathbf {p}_{n}\|_{2}\left[\cos\theta_{n}-\max_{t\in [0,1 ]}{\frac{\|\nabla F(\mathbf{a}_{n}-t\gamma_{n}\mathbf{p}_{n})-\nabla F(\mathbf{a}_ {n})\|_{2}}{\|\nabla F(\mathbf{a}_{n})\|_{2}}}\right]}$

( 1 )

Diese Ungleichung impliziert, dass der Betrag, um den wir sicher sein können, dass die Funktion verringert wird, von einem Kompromiss zwischen den beiden Termen in eckigen Klammern abhängt. Der erste Term in eckigen Klammern misst den Winkel zwischen der Abstiegsrichtung und der negativen Steigung. Der zweite Term misst, wie schnell sich der Gradient entlang der Abstiegsrichtung ändert. ${\displaystyle F}$

Grundsätzlich Ungleichheit ( 1 ) könnte optimiert werden , über und um eine optimale Schrittgröße und die Richtung zu wählen. Das Problem besteht darin, dass die Auswertung des zweiten Termes in eckigen Klammern die Auswertung von erfordert und zusätzliche Gradientenauswertungen im Allgemeinen teuer und unerwünscht sind. Einige Möglichkeiten, dieses Problem zu umgehen, sind: ${\displaystyle \mathbf {p} _{n}}$${\displaystyle \gamma_{n}}$${\displaystyle \nabla F(\mathbf{a}_{n}-t\gamma_{n}\mathbf{p}_{n})}$

• Verzichten Sie mit der Einstellung auf die Vorteile einer cleveren Abstiegsrichtung und verwenden Sie die Liniensuche , um eine geeignete Schrittweite zu finden , die beispielsweise die Wolfe-Bedingungen erfüllt .${\displaystyle \mathbf{p}_{n}=\nabla F(\mathbf{a_{n}})}$${\displaystyle \gamma_{n}}$
• Unter der Annahme, dass dies zweimal differenzierbar ist, verwenden Sie dessen Hessian, um zu schätzen. Dann wähle und Optimiere die Ungleichung ( 1 ).${\displaystyle F}$${\displaystyle \nabla ^{2}F}$${\displaystyle \|\nabla F(\mathbf {a}_{n}-t\gamma_{n}\mathbf {p}_{n})-\nabla F(\mathbf {a}_{n} )\|_{2}\approx \|t\gamma_{n}\nabla^{2}F(\mathbf{a}_{n})\mathbf{p}_{n}\|.}$${\displaystyle \mathbf {p} _{n}}$${\displaystyle \gamma_{n}}$
• Angenommen, dies ist Lipschitz , verwenden Sie ihre Lipschitz-Konstante, um dann zu wählen und zu binden , indem Sie die Ungleichung ( 1 ) optimieren .${\displaystyle \nabla F}$${\displaystyle L}$${\displaystyle \|\nabla F(\mathbf {a}_{n}-t\gamma_{n}\mathbf {p}_{n})-\nabla F(\mathbf {a}_{n} )\|_{2}\leq Lt\gamma_{n}\|\mathbf{p}_{n}\|.}$${\displaystyle \mathbf {p} _{n}}$${\displaystyle \gamma_{n}}$
• Erstellen Sie ein benutzerdefiniertes Modell von für . Wählen Sie dann und durch Optimierung der Ungleichung ( 1 ).${\displaystyle \max _{t\in [0,1]}{\frac {\|\nabla F(\mathbf {a} _{n}-t\gamma_{n}\mathbf {p} _{ n})-\nabla F(\mathbf{a}_{n})\|_{2}}{\|\nabla F(\mathbf{a}_{n})\|_{2}}} }$${\displaystyle F}$${\displaystyle \mathbf {p} _{n}}$${\displaystyle \gamma_{n}}$
• Unter stärkeren Annahmen über die Funktion wie Konvexität sind möglicherweise fortgeschrittenere Techniken möglich.${\displaystyle F}$

Normalerweise kann die Konvergenz zu einem lokalen Minimum durch Befolgen eines der obigen Rezepte garantiert werden. Wenn die Funktion ist konvex , sind alle lokalen Minima auch globalen Minima, also in diesem Fall Gradientenabfallsaktualisierung zur globalen Lösung konvergieren kann. ${\displaystyle F}$

Lösung eines linearen Systems

Der Algorithmus des steilsten Abstiegs, der auf das Wiener-Filter angewendet wird

Gradientenabstieg kann verwendet werden, um ein System linearer Gleichungen zu lösen

${\displaystyle A\mathbf{x} -\mathbf{b} =0}$

als quadratisches Minimierungsproblem umformuliert. Wenn die Systemmatrix real ist symmetrisch und positiv definit wird eine Zielfunktion , wie die quadratische Funktion definiert ist , mit Minimierung ${\displaystyle A}$

${\displaystyle F(\mathbf {x} )=\mathbf {x} ^{T}A\mathbf {x} -2\mathbf {x} ^{T}\mathbf {b} ,}$

so dass

${\displaystyle\nabla F(\mathbf{x})=2(A\mathbf{x} -\mathbf{b}).}$

Für eine allgemeine reelle Matrix , linearen kleinsten Quadrate definieren ${\displaystyle A}$

${\displaystyle F(\mathbf{x})=\left\|A\mathbf{x} -\mathbf{b}\right\|^{2}.}$

In traditionellen linearen kleinsten Quadraten für reelle und die euklidische Norm wird verwendet, in diesem Fall ${\displaystyle A}$${\displaystyle\mathbf{b}}$

${\displaystyle\nabla F(\mathbf{x})=2A^{T}(A\mathbf{x} -\mathbf{b}).}$

Die Liniensuchminimierung , die bei jeder Iteration die lokal optimale Schrittweite findet, kann für quadratische Funktionen analytisch durchgeführt werden, und explizite Formeln für das lokal optimale sind bekannt. ${\displaystyle\gamma}$${\displaystyle\gamma}$

Zum Beispiel kann für reelle symmetrische und positiv-definite Matrix ein einfacher Algorithmus wie folgt aussehen: ${\displaystyle A}$

${\displaystyle {\begin{ausgerichtet}&{\text{Wiederholung in der Schleife:}}\\&\qquad \mathbf {r} :=\mathbf {b} -\mathbf {Ax} \\&\qquad \ gamma :={\mathbf {r} ^{\mathsf {T}}\mathbf {r} }/{\mathbf {r} ^{\mathsf {T}}\mathbf {Ar} }\\&\qquad\ mathbf {x} :=\mathbf {x} +\gamma \mathbf {r} \\&\qquad {\hbox{if}}\mathbf {r} ^{\mathsf {T}}\mathbf {r} { \text{ ist hinreichend klein, dann Schleife beenden}}\\&{\text{Ende der Wiederholungsschleife}}\\&{\text{return }}\mathbf {x} {\text{ als Ergebnis}}\end {ausgerichtet}}}$

Um eine Multiplikation mit dem Doppelten pro Iteration zu vermeiden , beachten wir, dass impliziert , was den traditionellen Algorithmus ergibt, ${\displaystyle A}$${\displaystyle\mathbf{x} :=\mathbf{x} +\gamma\mathbf{r}}$${\displaystyle\mathbf{r} :=\mathbf{r} -\gamma\mathbf{Ar}}$

${\displaystyle {\begin{aligned}&\mathbf {r} :=\mathbf {b} -\mathbf {Ax} \\&{\text{Wiederholung in der Schleife:}}\\&\qquad \gamma : ={\mathbf {r} ^{\mathsf {T}}\mathbf {r} }/{\mathbf {r} ^{\mathsf {T}}\mathsf {Ar}}\&\qquad \mathbf { x} :=\mathbf {x} +\gamma \mathbf {r} \\&\qquad {\hbox{if}}\mathbf {r} ^{\mathsf {T}}\mathbf {r} {\text { ist ausreichend klein, dann Schleife beenden}}\\&\qquad \mathbf {r} :=\mathbf {r} -\gamma \mathbf {Ar} \\&{\text{Ende der Wiederholungsschleife}}\\& {\text{return }}\mathbf {x} {\text{ als Ergebnis}}\end{aligned}}}$

Die Methode wird selten zum Lösen linearer Gleichungen verwendet, wobei die konjugierte Gradientenmethode eine der beliebtesten Alternativen ist. Die Anzahl der Gradientenabstieg Iterationen ist auf die spektrale üblicherweise proportional Konditionszahl der Systemmatrix (das Verhältnis der maximalen zu der minimalen Eigenwerte von ) , während die Konvergenz der konjugierten Gradientenmethode typischerweise durch eine Quadratwurzel der Konditionszahl bestimmt wird, das heißt , ist viel schneller. Beide Methoden können von der Vorkonditionierung profitieren , bei der der Gradientenabstieg möglicherweise weniger Annahmen über den Vorkonditionierer erfordert. ${\displaystyle \kappa(A)}$${\displaystyle A}$${\displaystyle A^{T}A}$

Lösung eines nichtlinearen Systems

Gradientenabstieg kann auch verwendet werden, um ein System nichtlinearer Gleichungen zu lösen . Unten ist ein Beispiel, das zeigt, wie der Gradientenabstieg verwendet wird, um nach drei unbekannten Variablen x ₁ , x ₂ und x ₃ aufzulösen . Dieses Beispiel zeigt eine Iteration des Gradientenabstiegs.

Betrachten Sie das nichtlineare Gleichungssystem

${\displaystyle {\begin{cases}3x_{1}-\cos(x_{2}x_{3})-{\tfrac {3}{2}}=0\\4x_{1}^{2}- 625x_{2}^{2}+2x_{2}-1=0\\\exp(-x_{1}x_{2})+20x_{3}+{\tfrac {10\pi -3}{3 }}=0\end{Fälle}}}$

Wir führen die zugehörige Funktion ein

${\displaystyle G(\mathbf{x})={\begin{bmatrix}3x_{1}-\cos(x_{2}x_{3})-{\tfrac {3}{2}}\\4x_{ 1}^{2}-625x_{2}^{2}+2x_{2}-1\\\exp(-x_{1}x_{2})+20x_{3}+{\tfrac {10\pi -3}{3}}\\\end{bmatrix}},}$

wo

${\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\\\end{bmatrix}}.}$

Man könnte nun die Zielfunktion definieren

${\displaystyle F(\mathbf{x})={\frac{1}{2}}G^{\mathrm {T}}(\mathbf{x})G(\mathbf{x})={\frac {1}{2}}\left[\left(3x_{1}-\cos(x_{2}x_{3})-{\frac {3}{2}}\right)^{2}+\ left(4x_{1}^{2}-625x_{2}^{2}+2x_{2}-1\right)^{2}+\left(\exp(-x_{1}x_{2}) +20x_{3}+{\frac {10\pi -3}{3}}\right)^{2}\right],}$

die wir versuchen zu minimieren. Als erste Vermutung verwenden wir

${\displaystyle \mathbf {x} ^{(0)}=\mathbf {0} ={\begin{bmatrix}0\\0\\0\\\end{bmatrix}}.}$

Wir wissen das

${\displaystyle \mathbf {x} ^{(1)}=\mathbf {0} -\gamma _{0}\nabla F(\mathbf {0} )=\mathbf {0} -\gamma _{0} J_{G}(\mathbf{0} )^{\mathrm{T}}G(\mathbf{0}),}$

wobei die Jacobi-Matrix gegeben ist durch ${\displaystyle J_{G}}$

${\displaystyle J_{G}(\mathbf{x})={\begin{bmatrix}3&\sin(x_{2}x_{3})x_{3}&\sin(x_{2}x_{3} )x_{2}\\8x_{1}&-1250x_{2}+2&0\\-x_{2}\exp {(-x_{1}x_{2})}&-x_{1}\exp( -x_{1}x_{2})&20\\\end{bmatrix}}.}$

Wir berechnen:

${\displaystyle J_{G}(\mathbf {0})={\begin{bmatrix}3&0&0\\0&2&0\\0&0&20\end{bmatrix}},\qquad G(\mathbf {0})={\begin{ bmatrix}-2.5\\-1\\10.472\end{bmatrix}}.}$

Daher

${\displaystyle \mathbf {x} ^{(1)}=\mathbf {0} -\gamma _{0}{\begin{bmatrix}-7.5\\-2\\209.44\end{bmatrix}},}$

und

${\displaystyle F(\mathbf {0})=0.5\left((-2.5)^{2}+(-1)^{2}+(10.472)^{2}\right)=58.456.}$

Eine Animation, die die ersten 83 Iterationen des Gradientenabstiegs zeigt, die auf dieses Beispiel angewendet wurden. Oberflächen sind Isooberflächen der aktuellen Schätzung und Pfeile zeigen die Abstiegsrichtung an. Aufgrund einer kleinen und konstanten Schrittweite ist die Konvergenz langsam.${\displaystyle F(\mathbf{x} ^{(n)})}$${\displaystyle \mathbf {x} ^{(n)}}$

Nun muss ein passender gefunden werden, so dass ${\displaystyle \gamma _{0}}$

${\displaystyle F\left(\mathbf {x} ^{(1)}\right)\leq F\left(\mathbf {x} ^{(0)}\right)=F(\mathbf {0} ) .}$

Dies kann mit jedem einer Vielzahl von getan wird Linie Suchalgorithmen. Man könnte auch einfach erraten, was gibt ${\displaystyle \gamma_{0}=0,001,}$

${\displaystyle \mathbf {x} ^{(1)}={\begin{bmatrix}0.0075\\0.002\\-0.20944\\\end{bmatrix}}.}$

Die Auswertung der Zielfunktion bei diesem Wert ergibt

${\displaystyle F\left(\mathbf{x}^{(1)}\right)=0.5\left((-2.48)^{2}+(-1.00)^{2}+(6.28)^{2 }\right)=23.306.}$

Die Abnahme vom Wert des nächsten Schrittes von ${\displaystyle F(\mathbf {0})=58.456}$

${\displaystyle F\left(\mathbf{x} ^{(1)}\right)=23.306}$

ist eine beträchtliche Abnahme der Zielfunktion. Weitere Schritte würden seinen Wert weiter reduzieren, bis eine ungefähre Lösung für das System gefunden wurde.

Kommentare

Der Gradientenabstieg funktioniert in Räumen beliebiger Dimensionen, sogar in unendlichdimensionalen. Im letzteren Fall ist der Suchraum typischerweise ein Funktionsraum , und man berechnet die Fréchet-Ableitung des zu minimierenden Funktionals, um die Abstiegsrichtung zu bestimmen.

Dass der Gradientenabstieg in beliebig vielen Dimensionen (mindestens endliche Zahl) funktioniert, kann als Folge der Cauchy-Schwarz-Ungleichung gesehen werden . Dieser Artikel beweist, dass der Betrag des inneren (Punkt-)Produkts zweier Vektoren beliebiger Dimension maximiert ist, wenn sie kollinear sind. Im Fall eines Gradientenabstiegs wäre dies der Fall, wenn der Vektor der unabhängigen Variablenanpassungen proportional zum Gradientenvektor der partiellen Ableitungen ist.

Der Gradientenabstieg kann viele Iterationen erfordern , um ein lokales Minimum mit der erforderlichen Genauigkeit zu berechnen , wenn die Krümmung in verschiedenen Richtungen für die gegebene Funktion sehr unterschiedlich ist. Für solche Funktionen heilt die Vorkonditionierung , die die Geometrie des Raums ändert, um die Funktionsniveausätze wie konzentrische Kreise zu formen , die langsame Konvergenz. Das Konstruieren und Anwenden der Vorkonditionierung kann jedoch rechenintensiv sein.

Der Gradientenabstieg kann mit einer Liniensuche kombiniert werden, um bei jeder Iteration die lokal optimale Schrittweite zu finden. Die Durchführung der Leitungssuche kann zeitaufwendig sein. Umgekehrt kann die Verwendung eines festen kleinen Werts zu einer schlechten Konvergenz führen. ${\displaystyle\gamma}$${\displaystyle\gamma}$

Bessere Alternativen können Verfahren sein, die auf dem Newton-Verfahren und der Inversion des Hessischen unter Verwendung von konjugierten Gradiententechniken basieren. Im Allgemeinen konvergieren solche Verfahren in weniger Iterationen, aber die Kosten jeder Iteration sind höher. Ein Beispiel ist die BFGS Methode , die bei jedem Schritt eine Matrix bei der Berechnung besteht , mit dem der Gradientenvektor multipliziert wird , in eine „besseren“ Richtung zu gehen, mit einer anspruchsvolleren kombinierte Linie Suchalgorithmus, den „besten“ Wert zu finden Für extrem Bei großen Problemen, bei denen die Computerspeicherprobleme dominieren, sollte eine Methode mit begrenztem Speicher wie L-BFGS anstelle von BFGS oder dem steilsten Abstieg verwendet werden. ${\displaystyle\gamma.}$

Gradientenabstieg kann als Anwendung der Eulerschen Methode zur Lösung gewöhnlicher Differentialgleichungen auf einen Gradientenfluss betrachtet werden . Diese Gleichung kann wiederum als optimaler Regler für das Regelsystem mit gegebener Rückkopplungsform hergeleitet werden . ${\displaystyle x'(t)=-\nabla f(x(t))}$${\displaystyle x'(t)=u(t)}$${\displaystyle u(t)}$${\displaystyle u(t)=-\nabla f(x(t))}$

Änderungen

Der Gradientenabstieg kann zu einem lokalen Minimum konvergieren und sich in der Nähe eines Sattelpunktes verlangsamen . Selbst bei uneingeschränkter quadratischer Minimierung entwickelt der Gradientenabstieg im Verlauf der Iterationen ein Zick-Zack-Muster aufeinanderfolgender Iterationen, was zu einer langsamen Konvergenz führt. Es wurden mehrere Modifikationen des Gradientenabstiegs vorgeschlagen, um diese Mängel zu beheben.

Schnelle Gradientenmethoden

Yurii Nesterov hat eine einfache Modifikation vorgeschlagen, die eine schnellere Konvergenz für konvexe Probleme ermöglicht und seitdem weiter verallgemeinert wurde. Für unbeschränkte glatte Probleme wird das Verfahren als schnelles Gradientenverfahren (FGM) oder beschleunigtes Gradientenverfahren (AGM) bezeichnet. Insbesondere wenn die differenzierbare Funktion konvex ist und ist Lipschitz , und es wird angenommen , dass nicht ist stark konvex , dann wird der Fehler in dem Ziel - Wert bei jedem Schritt erzeugt durch das Gradientenabstiegsverfahren wird durch begrenzt . Unter Verwendung der Nesterov-Beschleunigungstechnik verringert sich der Fehler bei . Es ist bekannt, dass die Rate für die Abnahme der Kostenfunktion für Optimierungsverfahren erster Ordnung optimal ist. Dennoch besteht die Möglichkeit, den Algorithmus durch Reduzierung des konstanten Faktors zu verbessern. Die optimierte Gradientenmethode (OGM) reduziert diese Konstante um den Faktor zwei und ist eine optimale Methode erster Ordnung für großskalige Probleme. ${\displaystyle F}$${\displaystyle \nabla F}$${\displaystyle F}$${\displaystyle k}$ ${\textstyle {\mathcal{O}}\left({\tfrac {1}{k}}\right)}$${\textstyle {\mathcal{O}}\left({\tfrac {1}{k^{2}}}\right)}$${\displaystyle {\mathcal{O}}\left({k^{-2}}\right)}$

Für eingeschränkte oder nicht glatte Probleme wird Nesterovs FGM als schnelles proximales Gradientenverfahren (FPGM) bezeichnet, eine Beschleunigung des proximalen Gradientenverfahrens .

Momentum- oder Heavy-Ball- Methode

Beim Versuch, das Zick-Zack-Muster des Gradientenabstiegs zu durchbrechen, verwendet die Impuls- oder Heavy-Ball-Methode einen Impulsterm in Analogie zu einer schweren Kugel, die auf der Oberfläche von Werten der minimierten Funktion gleitet, oder zu einer Massenbewegung in der Newtonschen Dynamik durch ein viskoses Medium in einem konservativen Kraftfeld. Der Gradientenabstieg mit Impuls merkt sich die Lösungsaktualisierung bei jeder Iteration und bestimmt die nächste Aktualisierung als Linearkombination des Gradienten und der vorherigen Aktualisierung. Für unbeschränkte quadratische Minimierung ist eine theoretische Konvergenzratenschranke des Heavy-Ball-Verfahrens asymptotisch dieselbe wie die des optimalen konjugierten Gradientenverfahrens .

Diese Technik wird im Stochastischen Gradientenabstieg#Momentum und als Erweiterung der Backpropagation- Algorithmen verwendet, die zum Trainieren künstlicher neuronaler Netze verwendet werden .

Erweiterungen

Der Gradientenabstieg kann erweitert werden, um Beschränkungen zu handhaben , indem eine Projektion auf den Satz von Beschränkungen eingeschlossen wird. Dieses Verfahren ist nur möglich, wenn die Projektion auf einem Computer effizient berechenbar ist. Unter geeigneten Annahmen konvergiert diese Methode. Dieses Verfahren ist ein spezieller Fall des Vorwärts-Rückwärts-Algorithmus für monotone Einschlüsse (der konvexe Programmierung und Variationsungleichungen umfasst ).

Siehe auch

Verweise

Weiterlesen

• Boyd, Stephen ; Vandenberghe, Lieven (2004). "Uneingeschränkte Minimierung" (PDF) . Konvexe Optimierung . New York: Cambridge University Press. S. 457–520. ISBN 0-521-83378-7.
• Chong, Edwin KP; ak, Stanislaw H. (2013). "Gradientenmethoden" . Eine Einführung in die Optimierung (vierte Aufl.). Hoboken: Wiley. S. 131–160. ISBN 978-1-118-27901-4.
• Himmelblau, David M. (1972). „Uneingeschränkte Minimierungsverfahren mit Derivaten“. Angewandte nichtlineare Programmierung . New York: McGraw-Hill. S. 63–132. ISBN 0-07-028921-2.

Externe Links

• Verwenden des Gradientenabstiegs in C++, Boost, Ublas für die lineare Regression
• Eine Reihe von Videos der Khan Academy bespricht den Gradientenaufstieg
• Online-Buch, das den Gradientenabstieg im Kontext eines tiefen neuronalen Netzwerks lehrt
• „Gradientenabstieg, wie neuronale Netze lernen“ . 3Blau1Braun . 16. Oktober 2017 – über YouTube .

arxiv.org/2108.1283