Injektive Funktion - Injective function

In der Mathematik ist eine injektive Funktion (auch bekannt als Injektion oder Eins-zu-Eins-Funktion ) eine Funktion f , die verschiedene Elemente auf verschiedene Elemente abbildet ; das heißt, f ( x ₁ ) = f ( x ₂ ) impliziert x ₁ = x ₂ . Mit anderen Worten, jedes Element des Kobereichs der Funktion ist das Abbild von höchstens einem Element seines Bereichs . Der Begriff Eins-zu-Eins-Funktion darf nicht mit Eins-zu-Eins-Korrespondenz verwechselt werden , die sich auf bijektive Funktionen bezieht , bei denen es sich um Funktionen handelt , bei denen jedes Element in der Kodomäne ein Bild von genau einem Element in der Domäne ist.

Ein Homomorphismus zwischen algebraischen Strukturen ist eine Funktion, die mit den Operationen der Strukturen kompatibel ist. Für alle gängigen algebraischen Strukturen und insbesondere für Vektorräume wird ein injektiver Homomorphismus auch Monomorphismus genannt . Im allgemeineren Kontext der Kategorientheorie unterscheidet sich die Definition eines Monomorphismus jedoch von der eines injektiven Homomorphismus. Dies ist somit ein Satz, dass sie für algebraische Strukturen äquivalent sind; siehe Homomorphismus § Monomorphismus für weitere Details.

Eine Funktion , die nicht injektiv ist, wird manchmal als Viele-zu-Eins bezeichnet. ${\displaystyle f}$

Definition

Sei eine Funktion, deren Definitionsbereich eine Menge ist Die Funktion heißt injektiv, vorausgesetzt für alle und in if dann ; das heißt, impliziert Äquivalent, wenn dann${\displaystyle f}$${\displaystyle X.}$${\displaystyle f}$${\displaystyle a}$${\displaystyle b}$${\displaystyle X,}$${\displaystyle f(a)=f(b),}$${\displaystyle a=b}$${\displaystyle f(a)=f(b)}$${\displaystyle a=b.}$${\displaystyle a\neq b,}$${\displaystyle f(a)\neq f(b).}$

Symbolisch,

$${\displaystyle \forall a,b\in X,\;\;f(a)=f(b)\Rightarrow a=b,}$$

$${\displaystyle \forall a,b\in X,\;\;a\neq b\Rightarrow f(a)\neq f(b).}$$

Beispiele

Injektive Funktionen. Schematische Interpretation in der kartesischen Ebene , definiert durch die Abbildung wobei Funktionsbereich , Funktionsbereich und Bild von Jede in Abbildungen auf genau eine eindeutige in Die eingekreisten Teile der Achsen repräsentieren Domänen- und Bereichsmengen – gemäß dem Standard Diagramme oben.${\displaystyle f:X\to Y,}$${\displaystyle y=f(x),}$ ${\displaystyle X=}$${\displaystyle Y=}$ ${\displaystyle\operatorname {im} (f)}$${\displaystyle f.}$${\displaystyle x}$${\displaystyle X}$${\displaystyle y}$${\displaystyle Y.}$

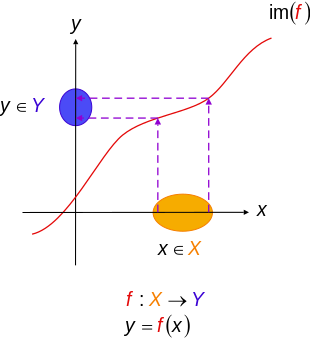
• Für jede Menge und jede Untermenge ist die Inklusionsabbildung (die jedes Element an sich selbst sendet ) injektiv. Insbesondere ist die Identitätsfunktion immer injektiv (und tatsächlich bijektiv).${\displaystyle X}$${\displaystyle S\subseteq X,}$ ${\displaystyle S\nach X}$${\displaystyle s\in S}$ ${\displaystyle X\nach X}$
• Wenn der Definitionsbereich einer Funktion die leere Menge ist , dann ist die Funktion die leere Funktion , die injektiv ist.
• Wenn der Definitionsbereich einer Funktion ein Element hat (also eine Singleton-Menge ist ), dann ist die Funktion immer injektiv.
• Die durch definierte Funktion ist injektiv.${\displaystyle f:\mathbb{R}\to\mathbb{R}}$${\displaystyle f(x)=2x+1}$
• Die durch definierte Funktion ist nicht injektiv, weil (zum Beispiel) wenn jedoch so umdefiniert wird, dass ihr Definitionsbereich die nicht-negativen reellen Zahlen [0,+∞ ist), dann ist injektiv.${\displaystyle g:\mathbb{R}\to\mathbb{R}}$${\displaystyle g(x)=x^{2}}$${\displaystyle g(1)=1=g(-1).}$${\displaystyle g}$${\displaystyle g}$
• Die durch definierte Exponentialfunktion ist injektiv (aber nicht surjektiv, da kein reeller Wert auf eine negative Zahl abgebildet wird).${\displaystyle \exp:\mathbb{R}\to\mathbb{R}}$${\displaystyle \exp(x)=e^{x}}$
• Die natürliche Logarithmus Funktion definiert durch injektiv.${\displaystyle \ln:(0,\infty)\to\mathbb{R}}$${\displaystyle x\mapsto\ln x}$
• Die durch definierte Funktion ist nicht injektiv, da z.${\displaystyle g:\mathbb{R}\to\mathbb{R}}$${\displaystyle g(x)=x^{n}-x}$${\displaystyle g(0)=g(1)=0.}$

Allgemeiner gesagt, wenn und beide die reelle Linie sind, ist eine injektive Funktion eine Funktion, deren Graph nie mehr als einmal von einer horizontalen Linie geschnitten wird. Dieses Prinzip wird als horizontaler Linientest bezeichnet . ${\displaystyle X}$${\displaystyle Y}$ ${\displaystyle\mathbb{R},}$${\displaystyle f:\mathbb{R}\to\mathbb{R}}$

Keine injektive Funktion. Hier und sind Teilmengen von und sind Teilmengen von : für zwei Regionen , in denen die Funktion nicht injektiv ist , weil mehr als eine Domäne Element zu einem einzigen Bereich Element zuordnen. Das heißt, ist es möglich , mehr als ein in zum abzubilden gleichen in${\displaystyle X_{1}}$${\displaystyle X_{2}}$${\displaystyle X,Y_{1}}$${\displaystyle Y_{2}}$${\displaystyle Y}$ ${\displaystyle x}$${\displaystyle X}$ ${\displaystyle y}$${\displaystyle Y.}$

Funktionen injektiv machen. Die vorherige Funktion kann auf eine oder mehrere injektive Funktionen reduziert werden (sagen wir) und durch durchgezogene Kurven dargestellt werden (langstrichige Teile der Anfangskurve werden nicht mehr abgebildet). Beachten Sie, dass sich die Regel nicht geändert hat – nur die Domäne und der Bereich. und sind Teilmengen von und sind Teilmengen von : für zwei Regionen, in denen die Anfangsfunktion injektiv gemacht werden kann, so dass ein Domänenelement auf ein einzelnes Bereichselement abgebildet werden kann. Das heißt, nur eine in Karten zu einer in${\displaystyle f:X\to Y}$${\displaystyle f:X_{1}\to Y_{1}}$${\displaystyle f:X_{2}\to Y_{2},}$${\displaystyle f}$${\displaystyle X_{1}}$${\displaystyle X_{2}}$${\displaystyle X,Y_{1}}$${\displaystyle Y_{2}}$${\displaystyle Y}$${\displaystyle x}$${\displaystyle X}$${\displaystyle y}$${\displaystyle Y.}$

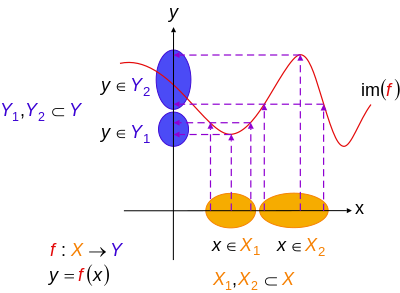
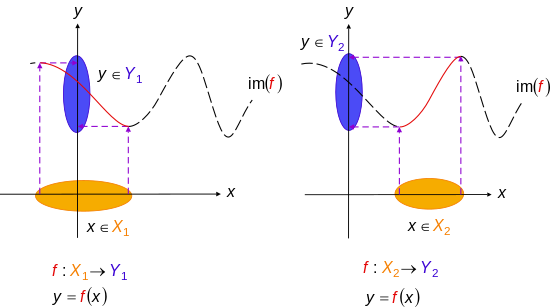
Injektionen können rückgängig gemacht werden

Funktionen mit Linksinversen sind immer Injektionen. Das heißt, wenn es eine Funktion gibt, so dass für jedes${\displaystyle f:X\to Y,}$${\displaystyle g:Y\to X}$${\displaystyle x\in X,}$

${\displaystyle g(f(x))=x}$( kann durch rückgängig gemacht werden ), dann ist injektiv. In diesem Fall heißt ein Rückzug von Umgekehrt heißt ein Abschnitt von${\displaystyle f}$${\displaystyle g}$${\displaystyle f}$${\displaystyle g}$${\displaystyle f.}$${\displaystyle f}$${\displaystyle g.}$

Umgekehrt hat jede Injektion mit nicht-leerem Bereich eine linke Inverse, die durch Fixieren eines Elements im Bereich von definiert werden kann, so dass es dem eindeutigen Vorbild von under entspricht, falls es existiert und ansonsten. ${\displaystyle f}$${\displaystyle g,}$${\displaystyle a}$${\displaystyle f}$${\displaystyle g(x)}$${\displaystyle x}$${\displaystyle f}$${\displaystyle g(x)=1}$

Die linke Inverse ist nicht unbedingt ein inverse von , weil die Zusammensetzung in der anderen Reihenfolge, von der Identität unterscheidet Mit anderen Worten kann eine injektivität sein „umgekehrt“ von einer links invers, ist aber nicht unbedingt umkehrbar , was erfordert , dass die Funktion ist bijektiv. ${\displaystyle g}$${\displaystyle f,}$${\displaystyle f\circ g,}$${\displaystyle Y.}$

Injektionen können invertierbar gemacht werden

In der Tat, eine injektivität zu drehen in eine bijektive (daher umkehrbar) Funktion genügt es , seine codomain zu ersetzen durch seine tatsächliche Reichweite Das heißt, es zu lassen , so dass für alle ; ist dann bijektiv. Tatsächlich kann berücksichtigt werden , da , wo die Aufnahme - Funktion von in${\displaystyle f:X\to Y}$${\displaystyle Y}$${\displaystyle J=f(X).}$${\displaystyle g:X\to J}$${\displaystyle g(x)=f(x)}$${\displaystyle x\in X}$${\displaystyle g}$${\displaystyle f}$${\displaystyle \operatorname {In} _{J,Y}\circ g,}$${\displaystyle \operatorname {In} _{J,Y}}$${\displaystyle J}$${\displaystyle Y.}$

Allgemeiner werden injektive Teilfunktionen als partielle Bijektionen bezeichnet .

Andere Eigenschaften

• Wenn und beide injektiv sind, dann ist injektiv.${\displaystyle f}$${\displaystyle g}$${\displaystyle f\circ g}$

Die Zusammensetzung zweier injektiver Funktionen ist injektiv.

• Wenn es injektiv ist, dann ist es injektiv (muss aber nicht sein).${\displaystyle g\circ f}$${\displaystyle f}$${\displaystyle g}$
• ${\displaystyle f:X\to Y}$ist genau dann injektiv, wenn gegebene Funktionen wann dann Mit anderen Worten, injektive Funktionen sind genau die Monomorphismen in der Kategorie Menge von Mengen.${\displaystyle g,}$ ${\displaystyle h:W\to X}$${\displaystyle f\circ g=f\circ h,}$${\displaystyle g=h.}$
• If ist injektiv und ist eine Teilmenge von Then Also, kann aus seinem Bild wiederhergestellt werden${\displaystyle f:X\to Y}$${\displaystyle A}$${\displaystyle X,}$${\displaystyle f^{-1}(f(A))=A.}$${\displaystyle A}$ ${\displaystyle f(A).}$
• If ist injektiv und und sind beide Teilmengen von then${\displaystyle f:X\to Y}$${\displaystyle A}$${\displaystyle B}$${\displaystyle X,}$${\displaystyle f(A\cap B)=f(A)\cap f(B).}$
• Jede Funktion kann hinsichtlich einer geeigneten Injektion und Surjektion zerlegt werden. Diese Zerlegung ist bis auf Isomorphie eindeutig und kann als Inklusionsfunktion des Bereichs von als Teilmenge der Kodomäne von betrachtet werden${\displaystyle h:W\to Y}$${\displaystyle h=f\circ g}$${\displaystyle f}$${\displaystyle g.}$${\displaystyle f}$${\displaystyle h(W)}$${\displaystyle h}$${\displaystyle Y}$${\displaystyle h.}$
• Ist eine injektive Funktion, dann hat sie mindestens so viele Elemente wie im Sinne von Kardinalzahlen . Insbesondere, wenn zusätzlich von bis dahin eine Injektion erfolgt und die gleiche Kardinalzahl haben. (Dies ist als Cantor-Bernstein-Schroeder-Theorem bekannt .)${\displaystyle f:X\to Y}$${\displaystyle Y}$${\displaystyle X,}$${\displaystyle Y}$${\displaystyle X,}$${\displaystyle X}$${\displaystyle Y}$
• Wenn beide und sind finite mit der gleichen Anzahl von Elementen, dann injektiv wenn und nur wenn surjektiv ist (in diesem Fall ist bijektives).${\displaystyle X}$${\displaystyle Y}$${\displaystyle f:X\to Y}$${\displaystyle f}$${\displaystyle f}$
• Eine injektive Funktion, die ein Homomorphismus zwischen zwei algebraischen Strukturen ist, ist eine Einbettung .
• Im Gegensatz zur Surjektivität, die eine Beziehung zwischen dem Graphen einer Funktion und ihrer Co-Domäne ist, ist die Injektivität eine Eigenschaft des Graphen der Funktion allein; das heißt, ob eine Funktion injektiv ist, kann nur durch die Betrachtung des Graphen (und nicht des Kobereichs) von entschieden werden${\displaystyle f}$${\displaystyle f.}$

Beweisen, dass Funktionen injektiv sind

Ein Beweis, dass eine Funktion injektiv ist, hängt davon ab, wie die Funktion präsentiert wird und welche Eigenschaften die Funktion besitzt. Für Funktionen, die durch eine Formel gegeben sind, gibt es eine Grundidee. Wir verwenden die Definition der Injektivität, nämlich dass wenn dann${\displaystyle f}$${\displaystyle f(x)=f(y),}$${\displaystyle x=y.}$

Hier ist ein Beispiel:

$${\displaystyle f(x)=2x+3}$$

Beweis: Angenommen, So impliziert was impliziert Daher folgt aus der Definition, die injektiv ist. ${\displaystyle f:X\nach Y.}$${\displaystyle f(x)=f(y).}$${\displaystyle 2x+3=2y+3}$${\displaystyle 2x=2y,}$${\displaystyle x=y.}$${\displaystyle f}$

Es gibt mehrere andere Methoden, um zu beweisen, dass eine Funktion injektiv ist. Wenn zum Beispiel in der Infinitesimalrechnung eine differenzierbare Funktion in einem Intervall definiert ist, dann genügt es zu zeigen, dass die Ableitung in diesem Intervall immer positiv oder immer negativ ist. In der linearen Algebra, wenn eine lineare Transformation ist, genügt es zu zeigen, dass der Kern von nur den Nullvektor enthält. Wenn es sich um eine Funktion mit endlicher Domäne handelt, reicht es aus, die Liste der Bilder jedes Domänenelements zu durchsuchen und zu überprüfen, dass kein Bild zweimal in der Liste vorkommt. ${\displaystyle f}$${\displaystyle f}$${\displaystyle f}$${\displaystyle f}$

Ein grafischer Ansatz für eine reellwertige Funktion einer reellen Variablen ist der horizontale Linientest . Wenn jede horizontale Linie die Kurve von in höchstens einem Punkt schneidet , dann ist injektiv oder eins zu eins. ${\displaystyle f}$${\displaystyle x}$${\displaystyle f(x)}$${\displaystyle f}$

Siehe auch

• Bijektion, Injektion und Surjektion  – Eigenschaften mathematischer Funktionen
• Injektiver metrischer Raum  – Art des metrischen Raums
• Monotone Funktion
• Univalente Funktion

Anmerkungen

Verweise

• Bartle, Robert G. (1976), The Elements of Real Analysis (2. Aufl.), New York: John Wiley & Sons , ISBN 978-0-471-05464-1, P. 17 ff .
• Halmos, Paul R. (1974), Naive Mengenlehre , New York: Springer, ISBN 978-0-387-90092-6, P. 38 ff .

Externe Links

• Früheste Verwendung einiger Wörter der Mathematik: Der Eintrag zu Injektion, Surjektion und Bijektion enthält die Geschichte der Injektion und verwandter Begriffe.
• Khan Academy – Surjektive (onto) und injektive (eins zu eins) Funktionen: Einführung in surjektive und injektive Funktionen