Lebesgue-Maßnahme - Lebesgue measure

In der Maßtheorie , einem Zweig der Mathematik , ist das Lebesgue-Maß , benannt nach dem französischen Mathematiker Henri Lebesgue , die Standardmethode, um Teilmengen des n- dimensionalen euklidischen Raums ein Maß zuzuweisen . Für n = 1, 2 oder 3 stimmt es mit dem Standardmaß für Länge , Fläche oder Volumen überein . Im Allgemeinen wird es auch n- dimensionales Volumen , n- Volumen oder einfach Volumen genannt . Es wird in der gesamten Realanalyse verwendet , insbesondere zur Definition der Lebesgue-Integration . Mengen, denen ein Lebesgue-Maß zugewiesen werden kann, werden als Lebesgue-messbar bezeichnet ; das Maß der Lebesgue-messbaren Menge A wird hier mit λ ( A ) bezeichnet.

Henri Lebesgue beschrieb dieses Maß im Jahr 1901, im nächsten Jahr folgte seine Beschreibung des Lebesgue-Integrals . Beide wurden 1902 im Rahmen seiner Dissertation veröffentlicht.

Das Lebesgue-Maß wird oft mit dx bezeichnet , aber dies sollte nicht mit dem eindeutigen Begriff einer Volumenform verwechselt werden .

Definition

Bezeichne für jedes Intervall (oder ) in der Menge der reellen Zahlen seine Länge. Für jede Teilmenge ist das äußere Maß von Lebesgue als Infimum definiert${\displaystyle I=[a,b]}$${\displaystyle I=(a,b)}$${\displaystyle \mathbb{R}}$${\displaystyle \ell(I)=ba}$${\displaystyle E\subseteq\mathbb{R}}$ ${\displaystyle \lambda ^{\!*\!}(E)}$

${\displaystyle \lambda^{\!*\!}(E)=\inf\left\{\sum _{k=1}^{\infty}\ell(I_{k}):{(I_{k .) })_{k\in\mathbb{N}}}{\text{ ist eine Folge von offenen Intervallen mit }}E\subset \bigcup_{k=1}^{\infty}I_{k}\right\ }.}$

Einige Sets erfüllen das Carathéodory-Kriterium , das verlangt, dass für jeden , ${\displaystyle E}$${\displaystyle A\subseteq\mathbb{R}}$

${\displaystyle \lambda ^{\!*\!}(A)=\lambda^{\!*\!}(A\cap E)+\lambda ^{\!*\!}(A\cap E^ {C}).}$

Die Menge aller solcher Formen bildet eine σ- Algebra . Für jeden solchen wird sein Lebesgue-Maß als sein Lebesgue-Außenmaß definiert: . ${\displaystyle E}$${\displaystyle E}$${\displaystyle \lambda(E)=\lambda^{\!*\!}(E)}$

Eine Menge , die das Carathéodory-Kriterium nicht erfüllt, ist nicht Lebesgue-messbar. Nicht messbare Mengen existieren; ein Beispiel sind die Vitali-Sets . ${\displaystyle E}$

Intuition

Der erste Teil der Definition besagt, dass die Teilmenge der reellen Zahlen durch die Überdeckung durch Mengen offener Intervalle auf ihr äußeres Maß reduziert wird. Jede dieser Intervallmengen deckt gewissermaßen ab, da die Vereinigung dieser Intervalle enthält . Die Gesamtlänge einer beliebigen überdeckenden Intervallmenge kann das Maß von überschätzen, da eine Teilmenge der Vereinigung der Intervalle ist, und daher können die Intervalle Punkte enthalten, die nicht in enthalten sind . Das äußere Maß von Lebesgue ergibt sich als die größte untere Schranke (Infimum) der Längen unter allen möglichen solchen Mengen. Intuitiv ist es die Gesamtlänge der Intervallsätze, die am engsten passen und sich nicht überlappen. ${\displaystyle E}$${\displaystyle I}$${\displaystyle E}$${\displaystyle E}$${\displaystyle E,}$${\displaystyle E}$${\displaystyle E}$${\displaystyle E}$

Das charakterisiert das Lebesgue-Außenmaß. Ob sich dieses äußere Maß in das eigentliche Lebesgue-Maß übersetzt, hängt von einer zusätzlichen Bedingung ab. Diese Bedingung wird getestet, indem Teilmengen der reellen Zahlen als Instrument verwendet werden, um in zwei Partitionen aufzuspalten : der Teil, der sich mit schneidet und der restliche Teil nicht in ist : die Mengendifferenz von und . Diese Unterteilungen unterliegen dem äußeren Maß. Wenn für alle möglichen solchen Teilmengen der reellen Zahlen die Partitionen von zerschnitten durch äußere Maße haben, deren Summe das äußere Maß von ist , dann gibt das äußere Lebesgue-Maß von sein Lebesgue-Maß an. Intuitiv bedeutet diese Bedingung, dass die Menge keine merkwürdigen Eigenschaften haben darf, die eine Diskrepanz im Maß einer anderen Menge verursacht, wenn sie als "Maske" zum "Ausschneiden" dieser Menge verwendet wird, was auf die Existenz von Mengen hinweist, für die die Lebesgue-Außen Maß gibt nicht das Lebesgue-Maß. (Solche Mengen sind tatsächlich nicht Lebesgue-messbar.) ${\displaystyle A}$${\displaystyle E}$${\displaystyle A}$${\displaystyle A}$${\displaystyle E}$${\displaystyle A}$${\displaystyle E}$${\displaystyle A}$${\displaystyle E}$${\displaystyle A}$${\displaystyle A}$${\displaystyle A}$${\displaystyle E}$${\displaystyle A}$${\displaystyle E}$${\displaystyle E}$${\displaystyle E}$

Beispiele

• Alles geschlossenes Intervall [ a , b ] der reellen Zahlen ist Lebesgue-messbar, und sein Lebesguemaß ist die Länge b - a . Das offene Intervall ( a , b ) hat das gleiche Maß, da die Differenz zwischen den beiden Mengen nur aus den Endpunkten a und b besteht und das Maß Null hat .
• Jedes kartesische Produkt der Intervalle [ a , b ] und [ c , d ] ist Lebesgue-messbar, und sein Lebesgue-Maß ist ( b − a )( d − c ) , die Fläche des entsprechenden Rechtecks .
• Darüber hinaus ist jeder Borel-Satz Lebesgue-messbar. Es gibt jedoch Lebesgue-messbare Mengen, die keine Borel-Mengen sind.
• Jede abzählbare Menge reeller Zahlen hat das Lebesgue-Maß 0. Insbesondere ist das Lebesgue-Maß der Menge der algebraischen Zahlen 0, obwohl die Menge in R dicht ist .
• Die Cantor-Menge und die Menge der Liouville-Zahlen sind Beispiele für unzählbare Mengen , die das Lebesgue-Maß 0 haben.
• Wenn das Bestimmtheitsaxiom gilt, dann sind alle Mengen von reellen Zahlen Lebesgue-messbar. Bestimmtheit ist jedoch nicht mit dem Auswahlaxiom vereinbar .
• Vitali-Mengen sind Beispiele für Mengen, die in Bezug auf das Lebesgue-Maß nicht messbar sind . Ihre Existenz beruht auf dem Auswahlaxiom .
• Osgood-Kurven sind einfache ebene Kurven mit positivem Lebesgue-Maß (kann durch kleine Variation der Peano-Kurvenkonstruktion erhalten werden). Die Drachenkurve ist ein weiteres ungewöhnliches Beispiel.
• Jede Zeile in , for hat ein Lebesgue-Maß null. Im Allgemeinen hat jede echte Hyperebene ein Null-Lebesgue-Maß in ihrem Umgebungsraum .${\displaystyle \mathbb{R} ^{n}}$${\displaystyle n\geq 2}$

Eigenschaften

Translationsinvarianz: Das Lebesgue-Maß von und ist gleich.${\displaystyle A}$${\displaystyle A+t}$

Das Lebesgue-Maß auf R ⁿ hat die folgenden Eigenschaften:

1. Ist A ein kartesisches Produkt der Intervalle I ₁ × I ₂ × ⋯ × I _n , dann ist A Lebesgue-messbar und hier gilt | ich | bezeichnet die Länge des Intervalls I .${\displaystyle \lambda(A)=|I_{1}|\cdot |I_{2}|\cdots |I_{n}|.}$
2. Wenn A eine ist disjunkte Vereinigung von abzählbar viele disjunkte Lebesgue-messbaren Mengen, dann A selbst Lebesgue-messbar und λ ( A ) ist gleich der Summe (oder unendliche Reihe ) der Maßnahmen der beteiligten messbaren Mengen.
3. Wenn A Lebesgue-messbar ist, dann ist es auch sein Komplement .
4. λ ( A ) ≥ 0 für jede Lebesgue-messbare Menge A .
5. Wenn A und B Lebesgue-messbar sind und A eine Teilmenge von B ist , dann gilt λ ( A ) ≤ λ ( B ). (Eine Folge von 2, 3 und 4.)
6. Abzählbare Vereinigungen und Schnittmengen von Lebesgue-messbaren Mengen sind Lebesgue-messbar. (Keine Folge von 2 und 3, da eine Familie von Mengen, die unter Komplementen und disjunkten abzählbaren Vereinigungen abgeschlossen ist, nicht unter abzählbaren Vereinigungen abgeschlossen werden muss: .)${\displaystyle \{\emptyset ,\{1,2,3,4\},\{1,2\},\{3,4\},\{1,3\},\{2,4\ }\}}$
7. Ist A eine offene oder abgeschlossene Teilmenge von R ⁿ (oder sogar Borel-Menge , siehe metrischer Raum ), dann ist A Lebesgue-messbar.
8. Wenn A eine Lebesgue-messbare Menge ist, dann ist sie "annähernd offen" und "annähernd abgeschlossen" im Sinne des Lebesgue-Maßes (siehe den Regularitätssatz zum Lebesgue-Maß ).
9. Eine Lebesgue-messbare Menge kann zwischen eine enthaltende offene Menge und eine enthaltene geschlossene Menge "gequetscht" werden. Diese Eigenschaft wurde als alternative Definition der Lebesgue-Messbarkeit verwendet. Genauer gesagt, ist Lebesgue genau dann messbar, wenn für alle eine offene und eine abgeschlossene Menge existieren, so dass und .${\displaystyle E\subset \mathbb{R}}$${\displaystyle \varepsilon >0}$${\displaystyle G}$${\displaystyle F}$${\displaystyle F\Teilmenge E\Teilmenge G}$${\displaystyle \lambda (G\setminus F)<\varepsilon}$
10. Ein Lebesgue-meßbare Menge kann „gequetscht“ zwischen einem enthaltenden G _δ Satz und ein enthaltenen F _σ . Dh wenn A Lebesgue-meßbar ist , dann existiert eine G _δ Satz G und ein F _σ F , so dass G  ⊇  A  ⊇  F und λ ( G  \  A ) =  λ ( A  \  F ) = 0.
11. Das Lebesgue-Maß ist sowohl lokal endlich als auch innerlich regelmäßig , also ein Radon-Maß .
12. Das Lebesgue-Maß ist auf nicht-leeren offenen Mengen strikt positiv , und daher ist seine Unterstützung das gesamte R ⁿ .
13. Ist A eine Lebesgue-messbare Menge mit λ( A ) = 0 (eine Nullmenge ), dann ist jede Teilmenge von A auch eine Nullmenge. Erst recht ist jede Teilmenge von A messbar.
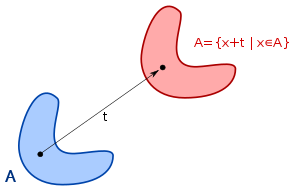
14. Ist A Lebesgue-messbar und x ein Element von R ⁿ , dann ist die Translation von A um x , definiert durch A + x = { a + x  : a ∈ A }, ebenfalls Lebesgue-messbar und hat das gleiche Maß wie Ein .
15. Ist A Lebesgue-messbar und , dann ist auch die Dilatation von durch definiert durch Lebesgue-messbar und hat Maß${\displaystyle \delta >0}$${\displaystyle A}$${\displaystyle\delta}$${\displaystyle \delta A=\{\delta x:x\in A\}}$${\displaystyle \delta^{n}\lambda\,(A).}$
16. Allgemeiner gesagt, wenn T eine lineare Transformation und A eine messbare Teilmenge von R ^{n ist} , dann ist T ( A ) auch Lebesgue-messbar und hat das Maß .${\displaystyle \left|\det(T)\right|\lambda(A)}$

All dies kann kurz wie folgt zusammengefasst werden (obwohl die letzten beiden Behauptungen nicht trivial mit dem Folgenden verbunden sind):

Die Lebesgue-meßbare Mengen bilden eine σ -Algebra alle Produkte von Intervallen enthalten, und λ ist die einzigartige vollständige translationsinvariant Maßnahme auf diesem σ-Algebra mit${\displaystyle \lambda ([0,1]\times [0,1]\times \cdots \times [0,1])=1.}$

Das Lebesgue-Maß hat auch die Eigenschaft, σ- endlich zu sein .

Nullsätze

Eine Teilmenge von R ⁿ ist eine Nullmenge, wenn sie für jedes ε > 0 mit abzählbar vielen Produkten von n Intervallen bedeckt werden kann, deren Gesamtvolumen höchstens ε ist. Alle zählbaren Mengen sind Nullmengen.

Wenn eine Teilmenge von R ⁿ eine Hausdorff-Dimension kleiner als n hat, dann ist sie eine Nullmenge in Bezug auf das n- dimensionale Lebesgue-Maß. Hier ist die Hausdorff-Dimension relativ zur euklidischen Metrik auf R ⁿ (oder einer ihr äquivalenten Metrik Lipschitz ). Andererseits kann eine Menge eine topologische Dimension von weniger als n haben und ein positives n- dimensionales Lebesgue-Maß haben. Ein Beispiel dafür ist die Smith-Volterra-Cantor-Menge, die die topologische Dimension 0 hat, aber ein positives 1-dimensionales Lebesgue-Maß hat.

Um zu zeigen, dass eine gegebene Menge A Lebesgue-messbar ist, versucht man normalerweise eine "schönere" Menge B zu finden, die sich von A nur durch eine Nullmenge unterscheidet (in dem Sinne, dass die symmetrische Differenz ( A − B ) ∪ ( B − A ) ist eine Nullmenge) und zeigen dann, dass B durch abzählbare Vereinigungen und Schnittmengen aus offenen oder geschlossenen Mengen erzeugt werden kann.

Bau der Lebesgue-Maßnahme

Die moderne Konstruktion des Lebesgue-Maßes ist eine Anwendung des Erweiterungssatzes von Carathéodory . Es geht wie folgt vor.

Fix n ∈ N . Eine Box in R ⁿ ist eine Menge der Form

${\displaystyle B=\prod_{i=1}^{n}[a_{i},b_{i}]\,,}$

wobei b _i ≥ a _i , und das Produktsymbol hier ein kartesisches Produkt darstellt. Das Volumen dieser Box ist definiert als

${\displaystyle \operatorname {vol} (B)=\prod_{i=1}^{n}(b_{i}-a_{i})\,.}$

Für jede Teilmenge A von R ⁿ können wir ihr äußeres Maß λ *( A ) definieren durch:

${\displaystyle \lambda ^{*}(A)=\inf\left\{\sum_{B\in {\mathcal {C}}}\operatorname {vol} (B):{\mathcal {C}} {\text{ ist eine abzählbare Sammlung von Kästchen, deren Vereinigung }}A\right\} umfasst.}$

Wir definieren dann das Set A Lebesgue-meßbar , wenn für jede Teilmenge zu S von R ⁿ ,

${\displaystyle \lambda^{*}(S)=\lambda^{*}(S\cap A)+\lambda^{*}(S\setminus A)\,.}$

Diese Lebesgue-messbaren Mengen bilden eine σ- Algebra , und das Lebesgue-Maß ist definiert durch λ ( A ) = λ * ( A ) für jede Lebesgue-messbare Menge A .

Die Existenz von Mengen, die nicht Lebesgue-messbar sind, ist eine Folge des mengentheoretischen Auswahlaxioms , das von vielen der herkömmlichen Axiomensysteme der Mengenlehre unabhängig ist . Der Vitali-Satz , der sich aus dem Axiom ergibt, besagt, dass es Teilmengen von R gibt , die nicht Lebesgue-messbar sind. Unter der Annahme des Auswahlaxioms wurden nicht messbare Mengen mit vielen überraschenden Eigenschaften demonstriert, wie zum Beispiel die des Banach-Tarski-Paradoxons .

1970 zeigte Robert M. Solovay , dass die Existenz von Mengen, die nicht Lebesgue-messbar sind, im Rahmen der Zermelo-Fraenkel-Mengentheorie ohne das Auswahlaxiom nicht beweisbar ist (siehe Solovays Modell ).

Beziehung zu anderen Maßnahmen

Das Borel-Maß stimmt mit dem Lebesgue-Maß in den Mengen überein, für die es definiert ist; es gibt jedoch viel mehr Lebesgue-messbare Mengen als Borel-messbare Mengen. Das Borel-Maß ist translationsinvariant, aber nicht vollständig .

Das Haar-Maß kann auf jeder lokal kompakten Gruppe definiert werden und ist eine Verallgemeinerung des Lebesgue-Maßes ( R ⁿ mit Addition ist eine lokal kompakte Gruppe).

Das Hausdorff-Maß ist eine Verallgemeinerung des Lebesgue-Maß, das zum Messen der Teilmengen von R ⁿ mit niedrigeren Dimensionen als n nützlich ist , wie Untermannigfaltigkeiten , zum Beispiel Flächen oder Kurven in R ³ und fraktale Mengen. Das Hausdorff-Maß ist nicht mit dem Begriff der Hausdorff-Dimension zu verwechseln .

Es kann gezeigt werden, dass es kein unendlich-dimensionales Analogon zum Lebesgue-Maß gibt .

Siehe auch

• Dichtesatz von Lebesgue
• Lebesgue-Maß der Menge der Liouville-Zahlen
• Nicht messbarer Satz
  • Vitali-Set

Verweise