Lineare Regression - Linear regression
| Teil einer Serie über |
| Regressionsanalyse |
|---|
| Modelle |
| Einschätzung |
| Hintergrund |
In der Statistik ist die lineare Regression ein linearer Ansatz zur Modellierung der Beziehung zwischen einer skalaren Antwort und einer oder mehreren erklärenden Variablen (auch als abhängige und unabhängige Variablen bekannt ). Der Fall einer erklärenden Variablen wird als einfache lineare Regression bezeichnet ; für mehr als eine wird der Prozess als multiple lineare Regression bezeichnet . Dieser Begriff unterscheidet sich von der multivariaten linearen Regression , bei der mehrere korrelierte abhängige Variablen vorhergesagt werden und nicht eine einzelne skalare Variable.
Verwendung in der linearen Regression werden die Beziehungen modellieren lineare Prädiktor Funktionen , deren unbekannten Modellparameter werden geschätzt aus den Daten . Solche Modelle werden lineare Modelle genannt . Am häufigsten wird angenommen, dass der bedingte Mittelwert der Antwort bei den Werten der erklärenden Variablen (oder Prädiktoren) eine affine Funktion dieser Werte ist; seltener wird der bedingte Median oder ein anderes Quantil verwendet. Wie alle Formen der Regressionsanalyse konzentriert sich die lineare Regression auf die bedingte Wahrscheinlichkeitsverteilung der Antwort anhand der Werte der Prädiktoren und nicht auf die gemeinsame Wahrscheinlichkeitsverteilung all dieser Variablen, die der Bereich der multivariaten Analyse ist .
Die lineare Regression war die erste Art der Regressionsanalyse, die gründlich untersucht und umfassend in praktischen Anwendungen eingesetzt wurde. Dies liegt daran, dass Modelle, die linear von ihren unbekannten Parametern abhängen, leichter anzupassen sind als Modelle, die nicht linear von ihren Parametern abhängig sind, und weil die statistischen Eigenschaften der resultierenden Schätzer leichter zu bestimmen sind.
Die lineare Regression hat viele praktische Anwendungen. Die meisten Anwendungen fallen in eine der folgenden zwei großen Kategorien:
- Wenn das Ziel Vorhersage , Vorhersage oder Fehlerreduzierung ist, kann die lineare Regression verwendet werden, um ein Vorhersagemodell an einen beobachteten Datensatz von Werten der Antwortvariablen und erklärenden Variablen anzupassen. Wenn nach der Entwicklung eines solchen Modells zusätzliche Werte der erklärenden Variablen ohne einen begleitenden Antwortwert gesammelt werden, kann das angepasste Modell verwendet werden, um eine Vorhersage der Antwort zu treffen.
- Wenn das Ziel darin besteht, die Variation der Antwortvariablen zu erklären, die auf die Variation der erklärenden Variablen zurückzuführen ist, kann die lineare Regressionsanalyse angewendet werden, um die Stärke der Beziehung zwischen der Antwort und den erklärenden Variablen zu quantifizieren und insbesondere zu bestimmen, ob einige erklärende Variablen möglicherweise überhaupt keine lineare Beziehung zur Antwort haben oder um zu identifizieren, welche Teilmengen von erklärenden Variablen redundante Informationen über die Antwort enthalten können.
Eine lineare Regressionsmodelle werden häufig mit dem ausgestattet kleinsten Quadrate nähern, sie können aber auch auf andere Weise angebracht werden, wie durch den „Mangel an fit“ in einer anderen minimiert Norm (wie bei dest absoluten Abweichungen Regression) oder durch eine Strafe zu minimieren Version der Kleinste-Quadrate- Kostenfunktion wie bei der Ridge-Regression ( L 2 -Normstrafe) und Lasso ( L 1 -Normstrafe). Umgekehrt kann der Ansatz der kleinsten Quadrate verwendet werden, um Modelle anzupassen, die keine linearen Modelle sind. Somit sind die Begriffe "kleinste Quadrate" und "lineares Modell" zwar eng miteinander verbunden, aber nicht synonym.
Formulierung
Bei einem gegebenen Datensatz von N statistischen Einheiten annimmt, ein lineares Regressionsmodell , dass die Beziehung zwischen der abhängigen Variablen y und p -vector der Regressoren x ist linear . Diese Beziehung wird durch eine modellierte Störterms oder Fehlervariablen ε - eine unbeobachtet Zufallsvariable , die „Rauschen“ an die lineare Beziehung zwischen der abhängigen Variable und Regressoren hinzufügt. Damit nimmt das Modell die Form an
wobei T die Transponierte bezeichnet , so dass x i T β das innere Produkt zwischen den Vektoren x i und β ist .
Oft werden diese n Gleichungen gestapelt und in Matrixschreibweise geschrieben als
wo
Notation und Terminologie
- ist ein Vektor beobachteter Werte der Variablen, die als Regressand , endogene Variable , Antwortvariable , gemessene Variable , Kriteriumsvariable oder abhängige Variable bezeichnet werden . Diese Variable wird manchmal auch als vorhergesagte Variable bezeichnet , sollte jedoch nicht mit vorhergesagten Werten verwechselt werden , die mit bezeichnet werden . Die Entscheidung, welche Variable in einem Datensatz als abhängige Variable modelliert wird und welche als unabhängige Variable modelliert wird, kann auf der Annahme beruhen, dass der Wert einer der Variablen durch die anderen Variablen verursacht oder direkt beeinflusst wird. Alternativ kann es einen operativen Grund geben, eine der Variablen in Bezug auf die anderen zu modellieren, wobei in diesem Fall keine Kausalitätsvermutung vorliegen muss.
-
kann als Matrix von Zeilenvektoren oder n- dimensionalen Spaltenvektoren angesehen werden , die als Regressoren , exogene Variablen , erklärende Variablen , Kovariaten , Eingabevariablen , Prädiktorvariablen oder unabhängige Variablen bekannt sind (nicht zu verwechseln mit dem Konzept von unabhängigen Zufallsvariablen ). Die Matrix wird manchmal als Entwurfsmatrix bezeichnet .
- Normalerweise ist eine Konstante als einer der Regressoren enthalten. Insbesondere für . Das entsprechende Element von
- Manchmal kann einer der Regressoren eine nichtlineare Funktion eines anderen Regressors oder der Daten sein, wie bei der polynomialen Regression und der segmentierten Regression . Das Modell bleibt linear, solange es im Parametervektor β linear ist .
- Die Werte x ij können entweder als beobachtete Werte von Zufallsvariablen X j oder als feste Werte angesehen werden, die vor der Beobachtung der abhängigen Variablen ausgewählt wurden. Beide Interpretationen können in unterschiedlichen Fällen angemessen sein und führen in der Regel zu den gleichen Schätzverfahren; jedoch werden in diesen beiden Situationen unterschiedliche Ansätze zur asymptotischen Analyse verwendet.
Das Anpassen eines linearen Modells an einen gegebenen Datensatz erfordert normalerweise die Schätzung der Regressionskoeffizienten, so dass der Fehlerterm minimiert wird. Beispielsweise ist es üblich, die Summe der quadrierten Fehler als Maß für die Minimierung zu verwenden.
Beispiel
Stellen Sie sich eine Situation vor, in der ein kleiner Ball in die Luft geworfen wird und wir dann seine Aufstiegshöhen h i zu verschiedenen Zeitpunkten t i messen . Die Physik sagt uns, dass die Beziehung ohne Berücksichtigung des Widerstands modelliert werden kann als
wobei β 1 die Anfangsgeschwindigkeit der Kugel bestimmt, β 2 proportional zur Standardschwerkraft ist und ε i auf Messfehler zurückzuführen ist. Die lineare Regression kann verwendet werden, um die Werte von β 1 und β 2 aus den gemessenen Daten abzuschätzen . Dieses Modell ist in der Zeitvariablen nicht linear, aber in den Parametern β 1 und β 2 linear ; wenn wir Regressoren x i = ( x i 1 , x i 2 ) = ( t i , t i 2 ) nehmen, nimmt das Modell die Standardform an
Annahmen
Standardmäßige lineare Regressionsmodelle mit Standardschätztechniken machen eine Reihe von Annahmen über die Prädiktorvariablen, die Antwortvariablen und ihre Beziehung. Es wurden zahlreiche Erweiterungen entwickelt, die es ermöglichen, jede dieser Annahmen zu lockern (dh auf eine schwächere Form zu reduzieren) und in einigen Fällen ganz zu eliminieren. Im Allgemeinen machen diese Erweiterungen das Schätzverfahren komplexer und zeitaufwendiger und können auch mehr Daten erfordern, um ein ebenso genaues Modell zu erstellen.
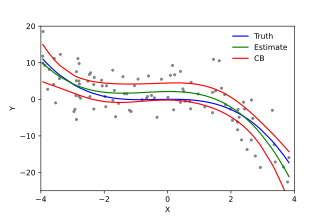
Im Folgenden sind die wichtigsten Annahmen von linearen Standardregressionsmodellen mit Standardschätztechniken (z. B. gewöhnliche kleinste Quadrate ) aufgeführt:
- Schwache Exogenität . Dies bedeutet im Wesentlichen, dass die Prädiktorvariablen x als feste Werte und nicht als Zufallsvariablen behandelt werden können . Dies bedeutet beispielsweise, dass die Prädiktorvariablen als fehlerfrei, also nicht mit Messfehlern verunreinigt, angenommen werden. Obwohl diese Annahme in vielen Situationen nicht realistisch ist, führt das Weglassen zu deutlich schwierigeren Fehler-in-Variablen-Modellen .
- Linearität . Dies bedeutet, dass der Mittelwert der Antwortvariablen eine Linearkombination der Parameter (Regressionskoeffizienten) und der Prädiktorvariablen ist. Beachten Sie, dass diese Annahme viel weniger restriktiv ist, als es auf den ersten Blick erscheinen mag. Da die Prädiktorvariablen als feste Werte behandelt werden (siehe oben), ist die Linearität eigentlich nur eine Einschränkung der Parameter. Die Prädiktorvariablen selbst können beliebig transformiert werden, und tatsächlich können mehrere Kopien derselben zugrunde liegenden Prädiktorvariablen hinzugefügt werden, wobei jede anders transformiert wird. Diese Technik wird beispielsweise bei der polynomialen Regression verwendet , die lineare Regression verwendet, um die Antwortvariable als willkürliche Polynomfunktion (bis zu einem bestimmten Rang) einer Prädiktorvariablen anzupassen. Bei dieser großen Flexibilität haben Modelle wie die polynomiale Regression oft "zu viel Macht", da sie dazu neigen, die Daten zu überfitten . Als Ergebnis muss typischerweise irgendeine Art von Regularisierung verwendet werden, um zu verhindern, dass unvernünftige Lösungen aus dem Schätzprozess herauskommen. Gängige Beispiele sind die Ridge-Regression und die Lasso-Regression . Es kann auch die Bayessche lineare Regression verwendet werden, die ihrer Natur nach mehr oder weniger immun gegen das Problem der Überanpassung ist. (Tatsächlich können die Ridge-Regression und die Lasso-Regression beide als Spezialfälle der Bayes'schen linearen Regression betrachtet werden, wobei den Regressionskoeffizienten bestimmte Arten von Prior-Verteilungen zugeordnet werden.)
- Konstante Varianz (auch bekannt als Homoskedastizität ). Dies bedeutet, dass die Varianz der Fehler nicht von den Werten der Prädiktorvariablen abhängt. Somit ist die Variabilität der Antworten für gegebene feste Werte der Prädiktoren gleich, unabhängig davon, wie groß oder klein die Antworten sind. Dies ist häufig nicht der Fall, da eine Variable mit einem großen Mittelwert typischerweise eine größere Varianz aufweist als eine Variable mit einem kleinen Mittelwert. Zum Beispiel kann eine Person, deren Einkommen auf 100.000 US-Dollar prognostiziert wird, leicht ein tatsächliches Einkommen von 80.000 US-Dollar oder 120.000 US-Dollar haben – dh eine Standardabweichung von etwa 20.000 US-Dollar –, während eine andere Person mit einem prognostizierten Einkommen von 10.000 US-Dollar wahrscheinlich dieselbe Standardabweichung von 20.000 US-Dollar hat , da dies bedeuten würde, dass ihr tatsächliches Einkommen zwischen -10.000 und 30.000 US-Dollar schwanken könnte. (Tatsächlich sollte, wie dies zeigt, in vielen Fällen – oft in den gleichen Fällen, in denen die Annahme normalverteilter Fehler fehlschlägt – die Varianz oder Standardabweichung als proportional zum Mittelwert und nicht als konstant vorhergesagt werden.) Das Fehlen von Homoskedastizität ist genannt heteroscedasticity . Um diese Annahme zu überprüfen, kann ein Diagramm von Residuen gegenüber vorhergesagten Werten (oder den Werten jedes einzelnen Prädiktors) auf einen "Auffächerungseffekt" untersucht werden (dh eine zunehmende oder abnehmende vertikale Streuung, wenn man sich auf dem Diagramm von links nach rechts bewegt). . Ein Diagramm der absoluten oder quadrierten Residuen gegenüber den vorhergesagten Werten (oder jedem Prädiktor) kann auch auf einen Trend oder eine Krümmung untersucht werden. Formale Tests können ebenfalls verwendet werden; siehe Heteroskedastizität . Das Vorhandensein von Heteroskedastizität führt dazu, dass eine "durchschnittliche" Schätzung der Varianz verwendet wird, anstatt eine, die die wahre Varianzstruktur berücksichtigt. Dies führt zu weniger präzisen (aber im Fall von gewöhnlichen kleinsten Quadraten nicht verzerrten) Parameterschätzungen und verzerrten Standardfehlern, was zu irreführenden Tests und Intervallschätzungen führt. Der mittlere quadratische Fehler für das Modell ist ebenfalls falsch. Verschiedene Schätztechniken, einschließlich gewichteter kleinster Quadrate und der Verwendung von heteroskedastizitätskonsistenten Standardfehlern, können Heteroskedastizität auf recht allgemeine Weise handhaben. Bayessche lineare Regressionstechniken können auch verwendet werden, wenn angenommen wird, dass die Varianz eine Funktion des Mittelwerts ist. Es ist auch möglich , in einigen Fällen das Problem zu beheben , indem eine Transformation auf die Antwortvariable Anwendung (zB Einpassen des Logarithmus der Reaktionsvariable ein lineares Regressionsmodell verwendet, was bedeutet , dass die Antwortvariable selbst eine hat Lognormalverteilung statt eine Normalverteilung ).
-
Unabhängigkeit von Fehlern . Dies setzt voraus, dass die Fehler der Antwortvariablen nicht miteinander korreliert sind. (Tatsächliche statistische Unabhängigkeit ist eine stärkere Bedingung als das bloße Fehlen von Korrelation und wird oft nicht benötigt, obwohl sie ausgenutzt werden kann, wenn sie bekannt ist.) Einige Methoden wie die verallgemeinerten kleinsten Quadrate sind in der Lage, korrelierte Fehler zu behandeln, obwohl sie normalerweise deutlich mehr Daten, es sei denn, eine Art Regularisierung wird verwendet, um das Modell dahingehend zu verzerren, unkorrelierte Fehler anzunehmen. Die Bayes'sche lineare Regression ist eine allgemeine Methode zur Behandlung dieses Problems.
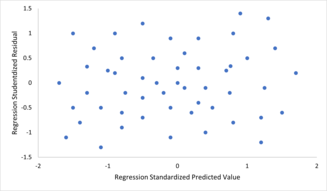 Um zu prüfen, ob die Annahmen der Linearität, der konstanten Varianz und der Fehlerunabhängigkeit innerhalb eines linearen Regressionsmodells verletzt sind, werden die Residuen typischerweise gegen die vorhergesagten Werte (oder jeden der einzelnen Prädiktoren) aufgetragen. Eine scheinbar zufällige Streuung von Punkten um die horizontale Mittellinie bei 0 ist ideal, kann aber bestimmte Arten von Verletzungen wie Autokorrelation in den Fehlern oder deren Korrelation mit einer oder mehreren Kovariaten nicht ausschließen.
Um zu prüfen, ob die Annahmen der Linearität, der konstanten Varianz und der Fehlerunabhängigkeit innerhalb eines linearen Regressionsmodells verletzt sind, werden die Residuen typischerweise gegen die vorhergesagten Werte (oder jeden der einzelnen Prädiktoren) aufgetragen. Eine scheinbar zufällige Streuung von Punkten um die horizontale Mittellinie bei 0 ist ideal, kann aber bestimmte Arten von Verletzungen wie Autokorrelation in den Fehlern oder deren Korrelation mit einer oder mehreren Kovariaten nicht ausschließen. - Mangel an perfekter Multikollinearität in den Prädiktoren. Für Standard- Schätzverfahren nach der Methode der kleinsten Quadrate muss die Entwurfsmatrix X den vollen Spaltenrang p haben ; andernfalls existiert in den Prädiktorvariablen eine perfekte Multikollinearität , was bedeutet, dass eine lineare Beziehung zwischen zwei oder mehr Prädiktorvariablen besteht. Dies kann durch versehentliches Duplizieren einer Variablen in den Daten verursacht werden, indem eine lineare Transformation einer Variablen zusammen mit dem Original verwendet wird (z. wie ihr Mittelwert. Dies kann auch passieren, wenn im Vergleich zur Anzahl der zu schätzenden Parameter zu wenig Daten verfügbar sind (zB weniger Datenpunkte als Regressionskoeffizienten). Beinahe Verletzungen dieser Annahme, bei denen Prädiktoren stark, aber nicht perfekt korreliert sind, können die Präzision von Parameterschätzungen verringern (siehe Varianzinflationsfaktor ). Im Fall einer perfekten multicollinearity, der Parametervektor β wird nicht identifizierbare -e hat keine eindeutige Lösung. In einem solchen Fall können nur einige der Parameter identifiziert werden (dh ihre Werte können nur innerhalb eines linearen Unterraums des vollständigen Parameterraums R p geschätzt werden ). Siehe partielle Regression der kleinsten Quadrate . Es wurden Methoden zur Anpassung linearer Modelle mit Multikollinearität entwickelt, von denen einige zusätzliche Annahmen erfordern, wie zum Beispiel „Effektsparsität“ – dass ein großer Teil der Effekte genau null ist. Beachten Sie, dass die rechenintensiveren iterierten Algorithmen zur Parameterschätzung, wie sie in verallgemeinerten linearen Modellen verwendet werden , nicht unter diesem Problem leiden.
Abgesehen von diesen Annahmen beeinflussen mehrere andere statistische Eigenschaften der Daten die Leistung verschiedener Schätzmethoden stark:
- Die statistische Beziehung zwischen den Fehlertermen und den Regressoren spielt eine wichtige Rolle bei der Bestimmung, ob ein Schätzverfahren wünschenswerte Sampling-Eigenschaften hat, wie z. B. unverzerrt und konsistent.
- Die Anordnung bzw. Wahrscheinlichkeitsverteilung der Prädiktorvariablen x hat einen großen Einfluss auf die Genauigkeit der Schätzungen von β . Probenahme und Versuchsplanung sind hochentwickelte Teilgebiete der Statistik, die eine Anleitung für die Sammlung von Daten bieten, um eine genaue Schätzung von β zu erreichen .
Interpretation

Ein angepasstes lineares Regressionsmodell kann verwendet werden, um die Beziehung zwischen einer einzelnen Prädiktorvariablen x j und der Antwortvariablen y zu identifizieren, wenn alle anderen Prädiktorvariablen im Modell "festgehalten" werden. Insbesondere ist die Interpretation von β j die erwartete Änderung von y für eine Änderung von x j um eine Einheit, wenn die anderen Kovariaten fest gehalten werden – d. h. der erwartete Wert der partiellen Ableitung von y in Bezug auf x j . Dies wird manchmal als einzigartiger Effekt von x j auf y bezeichnet . Im Gegensatz dazu kann der marginale Effekt von x j auf y unter Verwendung eines Korrelationskoeffizienten oder eines einfachen linearen Regressionsmodells bewertet werden , das nur x j auf y bezieht ; dieser Effekt ist die totale Ableitung von y nach x j .
Bei der Interpretation von Regressionsergebnissen ist Vorsicht geboten, da einige der Regressoren möglicherweise keine geringfügigen Änderungen berücksichtigen (wie Dummy-Variablen oder der Intercept-Term), während andere nicht fest gehalten werden können (erinnern Sie sich an das Beispiel aus der Einleitung: es wäre unmöglich um " t i fest zu halten " und gleichzeitig den Wert von t i 2 zu ändern ).
Es ist möglich, dass der einzigartige Effekt sogar bei einem großen marginalen Effekt nahezu null sein kann. Dies kann bedeuten, dass eine andere Kovariate alle Informationen in x j erfasst , so dass, sobald diese Variable im Modell ist, kein Beitrag von x j zur Variation in y vorhanden ist . Umgekehrt kann der eindeutige Effekt von x j groß sein, während sein marginaler Effekt nahezu null ist. Dies würde passieren, wenn die anderen Kovariaten einen großen Teil der Variation von y erklären würden, aber hauptsächlich die Variation auf eine Weise erklären, die komplementär zu dem ist, was von x j erfasst wird . In diesem Fall verringert das Einbeziehen der anderen Variablen in das Modell den Teil der Variabilität von y , der keinen Bezug zu x j hat , wodurch die scheinbare Beziehung zu x j verstärkt wird .
Die Bedeutung des Ausdrucks "fest gehalten" kann davon abhängen, wie die Werte der Prädiktorvariablen entstehen. Wenn der Experimentator die Werte der Prädiktorvariablen direkt gemäß einem Studiendesign festlegt, können die interessierenden Vergleiche buchstäblich Vergleichen zwischen Einheiten entsprechen, deren Prädiktorvariablen vom Experimentator "festgehalten" wurden. Alternativ kann sich der Ausdruck "festgehalten" auf eine Auswahl beziehen, die im Rahmen einer Datenanalyse erfolgt. In diesem Fall "halten wir eine Variable fest", indem wir unsere Aufmerksamkeit auf die Teilmengen der Daten beschränken, die zufällig einen gemeinsamen Wert für die gegebene Prädiktorvariable haben. Dies ist die einzige Interpretation von "festgehalten", die in einer Beobachtungsstudie verwendet werden kann.
Die Vorstellung eines "einzigartigen Effekts" ist reizvoll, wenn ein komplexes System untersucht wird, in dem mehrere miteinander zusammenhängende Komponenten die Antwortvariable beeinflussen. In manchen Fällen kann es wörtlich als kausaler Effekt einer Intervention interpretiert werden, der mit dem Wert einer Prädiktorvariablen verknüpft ist. Es wurde jedoch argumentiert, dass die multiple Regressionsanalyse in vielen Fällen die Beziehungen zwischen den Prädiktorvariablen und der Antwortvariablen nicht aufklären kann, wenn die Prädiktoren miteinander korreliert und nicht einem Studiendesign zugeordnet werden.
Erweiterungen
Es wurden zahlreiche Erweiterungen der linearen Regression entwickelt, die es erlauben, einige oder alle Annahmen, die dem Basismodell zugrunde liegen, zu lockern.
Einfache und mehrfache lineare Regression

Der einfachste Fall einer einzelnen skalaren Prädiktorvariablen x und einer einzelnen skalaren Antwortvariablen y ist als einfache lineare Regression bekannt . Die Erweiterung auf multiple und/oder vektorwertige Prädiktorvariablen (mit einem großen X gekennzeichnet ) ist als multiple lineare Regression bekannt , auch bekannt als multivariable lineare Regression (nicht zu verwechseln mit multivariater linearer Regression ).
Multiple lineare Regression ist eine Verallgemeinerung der einfachen linearen Regression auf den Fall von mehr als einer unabhängigen Variablen und ein Spezialfall allgemeiner linearer Modelle, beschränkt auf eine abhängige Variable. Das Basismodell für die multiple lineare Regression ist
für jede Beobachtung i = 1, ... , n .
In der obigen Formel betrachten wir n Beobachtungen einer abhängigen Variablen und p unabhängige Variablen. Somit ist Y i die i- te Beobachtung der abhängigen Variablen, X ij ist die i- te Beobachtung der j- ten unabhängigen Variablen, j = 1, 2, ..., p . Die Werte β j repräsentieren Parameter geschätzt werden, und & egr; i das ist i - ten unabhängig identisch verteilt normalen Fehler.
In der allgemeineren multivariaten linearen Regression gibt es eine Gleichung der obigen Form für jede von m > 1 abhängigen Variablen, die denselben Satz erklärender Variablen teilen und daher gleichzeitig miteinander geschätzt werden:
für alle mit i = 1, ... , n indizierten Beobachtungen und für alle mit j = 1, ... , m indizierten abhängigen Variablen .
Fast alle Regressionsmodelle der realen Welt beinhalten mehrere Prädiktoren, und grundlegende Beschreibungen der linearen Regression werden oft im Sinne des multiplen Regressionsmodells formuliert. Beachten Sie jedoch, dass die Antwortvariable y in diesen Fällen immer noch ein Skalar ist. Ein anderer Begriff, multivariate lineare Regression , bezieht sich auf Fälle, in denen y ein Vektor ist, dh dasselbe wie allgemeine lineare Regression .
Allgemeine lineare Modelle
Das allgemeine lineare Modell berücksichtigt die Situation, in der die Antwortvariable kein Skalar (für jede Beobachtung), sondern ein Vektor y i ist . Es wird weiterhin eine bedingte Linearität von angenommen, wobei eine Matrix B den Vektor β des klassischen linearen Regressionsmodells ersetzt. Multivariate Analoga von gewöhnlichen kleinsten Quadraten (OLS) und verallgemeinerten kleinsten Quadraten (GLS) wurden entwickelt. "Allgemeine lineare Modelle" werden auch "multivariate lineare Modelle" genannt. Diese sind nicht dasselbe wie lineare Modelle mit mehreren Variablen (auch "mehrere lineare Modelle" genannt).
Heteroskedastische Modelle
Es wurden verschiedene Modelle erstellt, die Heteroskedastizität berücksichtigen , dh die Fehler für verschiedene Antwortvariablen können unterschiedliche Varianzen aufweisen . Zum Beispiel gewichteten kleinsten Quadrate ist ein Verfahren zum Abschätzen lineare Regressionsmodelle , wenn die Antwortvariablen unterschiedliche Fehlervarianzen haben kann, möglicherweise mit korrelierten Fehler. (Siehe auch Gewichtete lineare kleinste Quadrate und verallgemeinerte kleinste Quadrate .) Heteroskedastizitäts-konsistente Standardfehler sind eine verbesserte Methode zur Verwendung mit unkorrelierten, aber potenziell heteroskedastischen Fehlern.
Verallgemeinerte lineare Modelle
Verallgemeinerte lineare Modelle (GLMs) sind ein Rahmen für die Modellierung von Antwortvariablen, die begrenzt oder diskret sind. Dies wird zum Beispiel verwendet:
- bei der Modellierung positiver Größen (z. B. Preise oder Populationen), die über eine große Skala variieren – die besser mit einer schiefen Verteilung wie der Log-Normalverteilung oder der Poisson-Verteilung beschrieben werden (obwohl GLMs nicht für Log-Normaldaten verwendet werden, sondern die Antwort Variable wird einfach mit der Logarithmusfunktion transformiert);
- bei der Modellierung kategorialer Daten , wie der Wahl eines bestimmten Kandidaten in einer Wahl (was besser mit einer Bernoulli-Verteilung / Binomialverteilung für binäre Wahlen oder einer kategorialen Verteilung / Multinomialverteilung für Mehrwege-Wahlmöglichkeiten beschrieben wird), wobei a feste Anzahl von Wahlmöglichkeiten, die nicht sinnvoll geordnet werden können;
- bei der Modellierung ordinaler Daten , z. B. Bewertungen auf einer Skala von 0 bis 5, bei denen die verschiedenen Ergebnisse geordnet werden können, die Menge selbst jedoch keine absolute Bedeutung hat (z. B. darf eine Bewertung von 4 in keinem Ziel "doppelt so gut" sein) Sinn als Bewertung von 2, sondern zeigt einfach an, dass es besser als 2 oder 3 ist, aber nicht so gut wie 5).
Verallgemeinerte lineare Modelle ermöglichen eine beliebige Verknüpfungsfunktion , g , die der bezieht Mittelwert der Antwortvariable (e) zu den Prädiktoren: . Die Verknüpfungsfunktion bezieht sich oft auf die Verteilung der Antwort und hat insbesondere die Wirkung, zwischen dem Bereich des linearen Prädiktors und dem Bereich der Antwortvariablen zu transformieren .
Einige gängige Beispiele für GLMs sind:
- Poisson-Regression für Zähldaten.
- Logistische Regression und Probit-Regression für Binärdaten.
- Multinomiale logistische Regression und multinomiale Probit- Regression für kategoriale Daten.
- Ordered Logit und Ordered Probit Regression für ordinale Daten.
Modelle mit einem einzigen Index erlauben ein gewisses Maß an Nichtlinearität in der Beziehung zwischen x und y , während die zentrale Rolle des linearen Prädiktors β ′ x wie im klassischen linearen Regressionsmodell beibehalten wird. Unter bestimmten Bedingungen wird β durch die einfache Anwendung von OLS auf Daten aus einem Einzelindexmodell konsistent bis zu einer Proportionalitätskonstante geschätzt .
Hierarchische lineare Modelle
Hierarchische lineare Modelle (oder mehrstufige Regression ) organisiert die Daten in eine Hierarchie von Regressionen, beispielsweise wobei A auf B regressiert wird und B auf C regressiert wird . Es wird häufig dort verwendet, wo die interessierenden Variablen eine natürliche hierarchische Struktur aufweisen, z. B. in der Bildungsstatistik, wo Schüler in Klassenzimmern verschachtelt sind, Klassenzimmer in Schulen verschachtelt sind und Schulen in einer administrativen Gruppierung wie einem Schulbezirk verschachtelt sind. Die Antwortvariable könnte ein Maß für die Leistung der Schüler sein, beispielsweise ein Testergebnis, und verschiedene Kovariaten würden auf Klassen-, Schul- und Schulbezirksebene gesammelt.
Fehler-in-Variablen
Fehler-in-Variablen-Modelle (oder "Messfehlermodelle") erweitern das traditionelle lineare Regressionsmodell, um zu ermöglichen, dass die Prädiktorvariablen X mit Fehlern beobachtet werden. Dieser Fehler führt dazu, dass Standardschätzer von β verzerrt werden. Im Allgemeinen ist die Form der Vorspannung eine Dämpfung, was bedeutet, dass die Effekte gegen Null vorgespannt sind.
Andere
- In der Dempster-Shafer-Theorie oder insbesondere einer linearen Glaubensfunktion kann ein lineares Regressionsmodell als teilweise gewobbelte Matrix dargestellt werden, die mit ähnlichen Matrizen kombiniert werden kann, die Beobachtungen und andere angenommene Normalverteilungen und Zustandsgleichungen darstellen. Die Kombination von gesweepten oder nicht gesweepten Matrizen bietet eine alternative Methode zum Schätzen von linearen Regressionsmodellen.
Schätzmethoden
Zur Parameterschätzung und Inferenz in der linearen Regression wurde eine Vielzahl von Verfahren entwickelt . Diese Methoden unterscheiden sich in der rechnerischen Einfachheit der Algorithmen, dem Vorhandensein einer Lösung in geschlossener Form, der Robustheit gegenüber stark taillierten Verteilungen und den theoretischen Annahmen, die erforderlich sind, um wünschenswerte statistische Eigenschaften wie Konsistenz und asymptotische Effizienz zu validieren .
Einige der gebräuchlicheren Schätztechniken für die lineare Regression sind unten zusammengefasst.
Angenommen, die unabhängige Variable ist und die Parameter des Modells sind , dann wäre die Vorhersage des Modells
- .
Wenn erweitert wird auf dann würde ein Punktprodukt des Parameters und der unabhängigen Variablen werden, dh
- .
In der Einstellung der kleinsten Quadrate wird der optimale Parameter als solcher definiert, der die Summe des mittleren quadratischen Verlustes minimiert:
Nun setzen die unabhängigen und abhängigen Variablen in Matrizen und jeweils kann die Verlustfunktion wie folgt umgeschrieben werden:
Da der Verlust konvex ist, liegt die optimale Lösung beim Gradienten Null. Der Gradient der Verlustfunktion ist (unter Verwendung der Nenner-Layout-Konvention ):
Die Einstellung des Gradienten auf Null ergibt den optimalen Parameter:
Anmerkung: Um zu beweisen, dass das Gesuchte tatsächlich das lokale Minimum ist, muss man noch einmal differenzieren, um die Hesse-Matrix zu erhalten und zu zeigen, dass sie positiv definit ist. Dies liefert der Satz von Gauss-Markov .
Zu den Methoden der linearen kleinsten Quadrate gehören hauptsächlich:
- Maximum - Likelihood - Schätzung durchgeführt werden kannwenn die Verteilung der Fehlerterme bekannt istbis zu einem gewissen parametrischen Familie gehört ƒ θ von Wahrscheinlichkeitsverteilungen . Wenn f θ eine Normalverteilung mit Null Mittelwert undVarianz θ ist die resultierende Schätzung identisch mit den OLS abzuschätzen. GLS-Schätzungen sind Maximum-Likelihood-Schätzungen, wenn ε einer multivariaten Normalverteilung mit einer bekannten Kovarianzmatrix folgt.
- Die Ridge-Regression und andere Formen der bestraften Schätzung, wie die Lasso-Regression , führen absichtlich einen Bias in die Schätzung von β ein, um die Variabilität der Schätzungzu reduzieren. Die resultierenden Schätzungen haben im Allgemeinen einen geringeren mittleren quadratischen Fehler als die OLS-Schätzungen, insbesondere wenn Multikollinearität vorliegt oder wenn Überanpassung ein Problem darstellt. Sie werden im Allgemeinen verwendet, wenn es darum geht, den Wert der Antwortvariablen y fürnoch nicht beobachteteWerte der Prädiktoren x vorherzusagen. Diese Methoden werden nicht so häufig verwendet, wenn das Ziel Inferenz ist, da es schwierig ist, den Bias zu berücksichtigen.
- Die Regression der kleinsten absoluten Abweichung (LAD) ist eine robuste Schätztechnik , da sie weniger empfindlich auf das Vorhandensein von Ausreißern reagiert als OLS (aber weniger effizient als OLS ist, wenn keine Ausreißer vorhanden sind). Sie ist äquivalent zur Schätzung der maximalen Wahrscheinlichkeit unter einem Laplace-Verteilungsmodell für ε .
- Adaptive Schätzung . Wenn wir davon ausgehen, dass Fehlerterme unabhängig von den Regressoren sind , dann ist der optimale Schätzer der 2-Stufen-MLE, wobei der erste Schritt verwendet wird, um die Verteilung des Fehlerterms nichtparametrisch zu schätzen.
Andere Schätztechniken

- Die Bayes'sche lineare Regression wendet den Rahmen der Bayes'schen Statistik auf die lineare Regression an. (Siehe auch Bayes'sche multivariate lineare Regression .) Insbesondere werden die Regressionskoeffizienten β als Zufallsvariablen mit einer bestimmten Vorverteilung angenommen . Die Prior-Verteilung kann die Lösungen für die Regressionskoeffizienten verzerren, ähnlich (aber allgemeiner als) der Ridge-Regression oder der Lasso-Regression . Darüber hinaus erzeugt das Bayessche Schätzverfahren keine einzelne Punktschätzung für die "besten" Werte der Regressionskoeffizienten, sondern eine gesamte Posterior-Verteilung , die die Unsicherheit um die Größe vollständig beschreibt. Dies kann verwendet werden, um die "besten" Koeffizienten unter Verwendung des Mittelwerts, des Modus, des Medians, eines beliebigen Quantils (siehe Quantilregression ) oder einer anderen Funktion der Posterior-Verteilungzu schätzen.
- Die Quantilregression konzentriert sich auf die bedingten Quantile von y bei gegebenem X und nicht auf den bedingten Mittelwert von y bei gegebenem X . Die lineare Quantilregression modelliert ein bestimmtes bedingtes Quantil, beispielsweise den bedingten Median, als lineare Funktion β T x der Prädiktoren.
- Gemischte Modelle werden häufig verwendet, um lineare Regressionsbeziehungen mit abhängigen Daten zu analysieren, wenn die Abhängigkeiten eine bekannte Struktur haben. Zu den üblichen Anwendungen von gemischten Modellen gehört die Analyse von Daten mit wiederholten Messungen, wie beispielsweise Längsschnittdaten oder Daten, die aus Cluster-Sampling gewonnen werden. Sie werden im Allgemeinen als parametrische Modelle angepasst , wobei die maximale Wahrscheinlichkeit oder die Bayessche Schätzung verwendet wird. Für den Fall, dass die Fehler als normale Zufallsvariablen modelliert werden, besteht ein enger Zusammenhang zwischen gemischten Modellen und verallgemeinerten kleinsten Quadraten. Die Schätzung fester Effekte ist ein alternativer Ansatz zur Analyse dieser Art von Daten.
- Die Hauptkomponentenregression (PCR) wird verwendet, wenn die Anzahl der Prädiktorvariablen groß ist oder wenn starke Korrelationen zwischen den Prädiktorvariablen bestehen. Dieses zweistufige Verfahren reduziert zuerst die Prädiktorvariablen unter Verwendung der Hauptkomponentenanalyse und verwendet dann die reduzierten Variablen in einer OLS-Regressionsanpassung. Obwohl es in der Praxis oft gut funktioniert, gibt es keinen allgemeinen theoretischen Grund dafür, dass die aussagekräftigste lineare Funktion der Prädiktorvariablen unter den dominanten Hauptkomponenten der multivariaten Verteilung der Prädiktorvariablen liegen sollte. Die partielle Regression der kleinsten Quadrate ist die Erweiterung der PCR-Methode, die nicht unter dem erwähnten Mangel leidet.
- Die Kleinstwinkelregression ist ein Schätzverfahren für lineare Regressionsmodelle, das entwickelt wurde, um hochdimensionale Kovariatenvektoren zu verarbeiten, möglicherweise mit mehr Kovariaten als Beobachtungen.
- Der Theil-Sen-Schätzer ist ein einfaches robustes Schätzverfahren , das die Steigung der Anpassungslinie als Median der Steigung der Linien durch Paare von Stichprobenpunkten wählt. Sie hat ähnliche statistische Effizienzeigenschaften wie die einfache lineare Regression, ist jedoch viel weniger empfindlich gegenüber Ausreißern .
- Andere robuste Schätztechniken, einschließlich des α-getrimmten Mittelwertansatzes und L-, M-, S- und R-Schätzer , wurden eingeführt.
Anwendungen
Lineare Regression wird häufig in den Bio-, Verhaltens- und Sozialwissenschaften verwendet, um mögliche Beziehungen zwischen Variablen zu beschreiben. Es gilt als eines der wichtigsten Werkzeuge in diesen Disziplinen.
Trendlinie
Eine Trendlinie stellt einen Trend dar, die langfristige Bewegung in Zeitreihendaten , nachdem andere Komponenten berücksichtigt wurden. Es sagt aus, ob ein bestimmter Datensatz (z. B. BIP, Ölpreise oder Aktienkurse) im Laufe der Zeit gestiegen oder gefallen ist. Eine Trendlinie könnte einfach mit dem Auge durch eine Reihe von Datenpunkten gezogen werden, aber genauer wird ihre Position und Steigung mit statistischen Techniken wie der linearen Regression berechnet. Trendlinien sind typischerweise gerade Linien, obwohl einige Variationen Polynome höheren Grades verwenden, abhängig vom gewünschten Krümmungsgrad der Linie.
Trendlinien werden manchmal in der Geschäftsanalyse verwendet, um Datenänderungen im Laufe der Zeit anzuzeigen. Dies hat den Vorteil, dass es einfach ist. Trendlinien werden oft verwendet, um zu argumentieren, dass eine bestimmte Aktion oder ein bestimmtes Ereignis (z. B. eine Schulung oder eine Werbekampagne) zu einem bestimmten Zeitpunkt beobachtete Veränderungen verursacht hat. Dies ist eine einfache Technik und erfordert keine Kontrollgruppe, kein experimentelles Design oder eine ausgeklügelte Analysetechnik. Es fehlt jedoch an wissenschaftlicher Validität, wenn andere potenzielle Änderungen die Daten beeinflussen können.
Epidemiologie
Frühe Beweise, die Tabakrauchen mit Mortalität und Morbidität in Verbindung brachten, stammten aus Beobachtungsstudien mit Regressionsanalyse. Um falsche Korrelationen bei der Analyse von Beobachtungsdaten zu reduzieren, beziehen Forscher neben der primär interessierenden Variablen in der Regel mehrere Variablen in ihre Regressionsmodelle ein. Beispielsweise könnten Forscher in einem Regressionsmodell, in dem das Zigarettenrauchen die unabhängige Variable von primärem Interesse ist und die abhängige Variable die in Jahren gemessene Lebensspanne ist, Bildung und Einkommen als zusätzliche unabhängige Variablen einbeziehen, um sicherzustellen, dass jeder beobachtete Effekt des Rauchens auf die Lebensspanne nicht aufgrund dieser anderen sozioökonomischen Faktoren . Allerdings ist es nie möglich , alle möglich sind verwirrende Variablen in einer empirischen Analyse. Ein hypothetisches Gen könnte beispielsweise die Sterblichkeit erhöhen und auch dazu führen, dass Menschen mehr rauchen. Aus diesem Grund sind randomisierte kontrollierte Studien oft in der Lage, aussagekräftigere Hinweise auf kausale Zusammenhänge zu generieren, als dies mit Regressionsanalysen von Beobachtungsdaten möglich ist. Wenn kontrollierte Experimente nicht durchführbar sind, können Varianten der Regressionsanalyse wie die Regression instrumenteller Variablen verwendet werden, um zu versuchen, kausale Zusammenhänge aus Beobachtungsdaten abzuschätzen.
Finanzen
Das Capital Asset Pricing Modell verwendet die lineare Regression sowie das Beta- Konzept zur Analyse und Quantifizierung des systematischen Risikos einer Anlage. Dies ergibt sich direkt aus dem Betakoeffizienten des linearen Regressionsmodells, das die Rendite der Anlage mit der Rendite aller riskanten Anlagen in Beziehung setzt.
Wirtschaft
Die lineare Regression ist das vorherrschende empirische Instrument der Wirtschaftswissenschaften . Zum Beispiel verwendet wird, um vorherzusagen Konsumausgaben , die Anlageinvestitionen der Ausgaben, Lagerinvestitionen , Einkäufe eines Landes der Exporte , die Ausgaben für Importe , die halte Nachfrage liquide Mittel , die Arbeitsnachfrage und Arbeitsangebot .
Umweltwissenschaft
Die lineare Regression findet Anwendung in einer Vielzahl von umweltwissenschaftlichen Anwendungen. In Kanada nutzen die Umweltauswirkungen Programmüberwachung statistische Analysen auf Fische und benthische Erhebungen die Auswirkungen der Zellstofffabrik oder Metall Minen - Abwassers auf dem aquatischen Ökosystem zu messen.
Maschinelles Lernen
Die lineare Regression spielt im Teilgebiet der künstlichen Intelligenz, dem sogenannten Machine Learning, eine wichtige Rolle . Der lineare Regressionsalgorithmus ist aufgrund seiner relativen Einfachheit und wohlbekannten Eigenschaften einer der grundlegenden überwachten maschinellen Lernalgorithmen .
Geschichte
Die lineare Regression der kleinsten Quadrate als Mittel zum Finden einer guten groben linearen Anpassung an eine Menge von Punkten wurde von Legendre (1805) und Gauss (1809) für die Vorhersage der Planetenbewegung durchgeführt. Quetelet war dafür verantwortlich, das Verfahren bekannt zu machen und in den Sozialwissenschaften umfassend einzusetzen.
Siehe auch
- Varianzanalyse
- Blinder-Oaxaca-Zersetzung
- Zensiertes Regressionsmodell
- Querschnittsregression
- Kurvenanpassung
- Empirische Bayes-Methoden
- Fehler und Residuen
- Unpassende Quadratsumme
- Leitungsanpassung
- Linearer Klassifikator
- Lineargleichung
- Logistische Regression
- M-Schätzer
- Multivariate adaptive Regressionssplines
- Nichtlineare Regression
- Nichtparametrische Regression
- Normalgleichungen
- Projektionsverfolgungsregression
- Reaktionsmodellierungsmethodik
- Segmentierte lineare Regression
- Schrittweise Regression
- Strukturbruch
- Support-Vektor-Maschine
- Abgeschnittenes Regressionsmodell
- Deming-Regression
Verweise
Zitate
Quellen
- Cohen, J., Cohen P., West, SG, & Aiken, LS (2003). Angewandte multiple Regressions-/Korrelationsanalyse für die Verhaltenswissenschaften . (2. Aufl.) Hillsdale, NJ: Lawrence Erlbaum Associates
- Charles Darwin . Die Variation von Tieren und Pflanzen unter Domestizierung . (1868) (Kapitel XIII beschreibt, was zu Galtons Zeiten über die Reversion bekannt war. Darwin verwendet den Begriff "Reversion".)
- Draper, NR; Schmidt, H. (1998). Angewandte Regressionsanalyse (3. Aufl.). John Wiley. ISBN 978-0-471-17082-2.
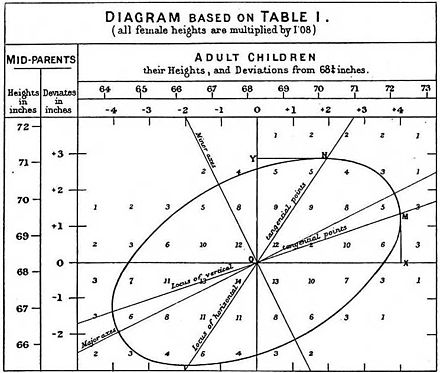
- Francis Galton. "Regression Towards Mittelmäßigkeit in erblicher Statur", Journal of the Anthropological Institute , 15: 246-263 (1886). (Faksimile unter: [1] )
- Robert S. Pindyck und Daniel L. Rubinfeld (1998, 4. Aufl.). Ökonometrische Modelle und Wirtschaftsprognosen , Kap. 1 (Intro, inkl. Anhänge zu Σ-Operatoren & Ableitung der Parameter est.) & Anhang 4.3 (multipl. Regression in Matrixform).
Weiterlesen
- Pedazur, Elazar J (1982). Multiple Regression in der Verhaltensforschung: Erklärung und Vorhersage (2. Aufl.). New York: Holt, Rinehart und Winston. ISBN 978-0-03-041760-3.
- Mathieu Rouaud, 2013: Wahrscheinlichkeit, Statistik und Schätzung Kapitel 2: Lineare Regression, Lineare Regression mit Fehlerbalken und Nichtlineare Regression.
- Nationales Physikalisches Labor (1961). „Kapitel 1: Lineare Gleichungen und Matrizen: Direkte Methoden“. Moderne Rechenmethoden . Hinweise zur angewandten Wissenschaft. 16 (2. Aufl.). Schreibwarenbüro Ihrer Majestät .
Externe Links
- Regression der kleinsten Quadrate , PhET Interaktive Simulationen, University of Colorado at Boulder
- DIY Lineare Passform






























![{\displaystyle {\vec {x_{i}}}=\left[x_{1}^{i},x_{2}^{i},\ldots ,x_{m}^{i}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/156ecace8a311d501c63ca49c73bba6efc915283)
![{\displaystyle {\vec {\beta}}=\left[\beta_{0},\beta_{1},\ldots,\beta_{m}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32434f0942d63c868f23d5af39442bb90783633b)


![{\displaystyle {\vec {x_{i}}}=\left[1,x_{1}^{i},x_{2}^{i},\ldots,x_{m}^{i}\right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72fa7acd1682497c285884b0686d784d8b0eb15)








