Nusselt-Nummer - Nusselt number

In der Fluiddynamik ist die Nusselt-Zahl ( Nu ) das Verhältnis von konvektiver zu konduktiver Wärmeübertragung an einer Grenzfläche in einer Flüssigkeit . Konvektion umfasst sowohl Advektion (Fluidbewegung) als auch Diffusion (Leitung). Die leitfähige Komponente wird unter den gleichen Bedingungen wie die konvektive gemessen, jedoch für eine hypothetisch bewegungslose Flüssigkeit. Es ist eine dimensionslose Zahl , die eng mit der Rayleigh-Zahl der Flüssigkeit verwandt ist .

Eine Nusselt-Zahl vom Wert eins repräsentiert die Wärmeübertragung durch reine Leitung. Ein Wert zwischen eins und 10 ist charakteristisch für Schwallströmung oder Laminarströmung . Eine größere Nusselt-Zahl entspricht einer aktiveren Konvektion, mit turbulenter Strömung typischerweise im Bereich von 100–1000. Die Nusselt-Zahl ist nach Wilhelm Nusselt benannt , der bedeutende Beiträge zur Wissenschaft der konvektiven Wärmeübertragung geleistet hat.

Eine ähnliche dimensionslose Eigenschaft ist die Biot-Zahl , die die Wärmeleitfähigkeit für einen Festkörper und nicht für eine Flüssigkeit betrifft . Das Stoffübergangsanalogon der Nusselt-Zahl ist die Sherwood-Zahl .

Definition

Die Nusselt-Zahl ist das Verhältnis von konvektiver zu konduktiver Wärmeübertragung über eine Grenze. Die Konvektions- und Wärmeleitungsströme verlaufen parallel zueinander und zur Flächennormalen der Grenzfläche und stehen im einfachen Fall alle senkrecht zur mittleren Fluidströmung.

${\displaystyle \mathrm {Nu} _{L}={\frac {\mbox{Konvektive Wärmeübertragung}}{\mbox{Konduktive Wärmeübertragung}}}={\frac {h}{k/L}}={ \frac {hL}{k}}}$

wobei h der konvektive Wärmeübergangskoeffizient der Strömung ist, L die charakteristische Länge ist , k die Wärmeleitfähigkeit des Fluids ist.

• Die Auswahl der charakteristischen Länge sollte in Wachstumsrichtung (oder Dicke) der Grenzschicht erfolgen; Einige Beispiele für charakteristische Längen sind: der Außendurchmesser eines Zylinders in (äußerer) Querströmung (senkrecht zur Zylinderachse), die Länge einer vertikalen Platte, die einer natürlichen Konvektion unterliegt , oder der Durchmesser einer Kugel. Bei komplexen Formen kann die Länge als das Volumen des Fluidkörpers geteilt durch die Oberfläche definiert werden.
• Die thermische Leitfähigkeit des Fluids ist in der Regel (aber nicht immer) bei der bewertete Folientemperatur , die für technische Zwecke kann als berechnet wird mittleres -Mittlere der Schüttfluidtemperatur und Wandoberflächentemperatur.

Im Gegensatz zu der oben gegebenen Definition, die als durchschnittliche Nusselt-Zahl bekannt ist , wird die lokale Nusselt-Zahl definiert, indem die Länge als der Abstand von der Oberflächengrenze zum lokalen interessierenden Punkt genommen wird.

${\displaystyle \mathrm {Nu} _{x}={\frac {h_{x}x}{k}}}$

Der Mittelwert oder Durchschnitt wird durch Integrieren des Ausdrucks über den interessierenden Bereich erhalten, wie zum Beispiel:

${\displaystyle {\overline {\mathrm {Nu}}}={\frac {{\frac {1}{L}}\int _{0}^{L}h_{x}\ dx\ L}{k }}={\frac {{\overline {h}}L}{k}}}$

Kontext

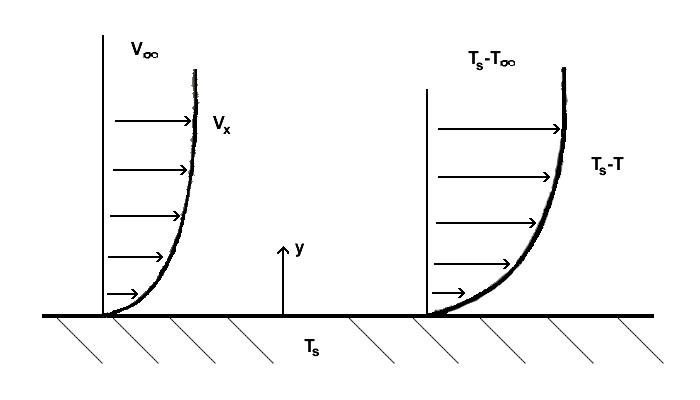
Um die konvektive Wärmeübertragung zwischen einer Oberfläche und einem daran vorbeiströmenden Fluid zu verstehen, ist ein Verständnis der Konvektionsgrenzschichten erforderlich. Eine thermische Grenzschicht entsteht, wenn die Temperatur des freien Strömungsmittelstroms und die Oberflächentemperaturen unterschiedlich sind. Durch den aus dieser Temperaturdifferenz resultierenden Energieaustausch existiert ein Temperaturprofil.

Die Wärmeübertragungsrate kann dann geschrieben werden als

${\displaystyle {{Q}_{y}}=hA\left({{T}_{s}}-{{T}_{\infty}}\right)}$

Und weil die Wärmeübertragung an der Oberfläche durch Leitung erfolgt,

${\displaystyle {{Q}_{y}}=-kA{\frac {\partial }{\partial y}}{{\left.\left(T-{{T}_{s}}\right) \right|}_{y=0}}}$

Diese beiden Begriffe sind gleich; daher

${\displaystyle -kA{\frac {\partial }{\partial y}}{{\left.\left(T-{{T}_{s}}\right)\right|}_{y=0} }=hA\left({{T}_{s}}-{{T}_{\infty}}\right)}$

Neuordnung,

${\displaystyle {\frac {h}{k}}={\frac {{\left.{\frac {\partial \left({{T}_{s}}-T\right)}{\partial y }}\right|}_{y=0}}{\left({{T}_{s}}-{{T}_{\infty}}\right)}}}$

Dimensionslos machen durch Multiplizieren mit der repräsentativen Länge L,

${\displaystyle {\frac {hL}{k}}={\frac {{\left.{\frac {\partial \left({{T}_{s}}-T\right)}{\partial y }}\right|}_{y=0}}{\frac {\left({{T}_{s}}-{{T}_{\infty}}\right)}{L}}}}$

Die rechte Seite ist nun das Verhältnis des Temperaturgradienten an der Oberfläche zum Referenztemperaturgradienten, während die linke Seite ähnlich dem Biot-Modul ist. Dies wird das Verhältnis des leitenden Wärmewiderstands zum konvektiven Wärmewiderstand des Fluids, auch bekannt als die Nusselt-Zahl Nu.

${\displaystyle \mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}}$

Ableitung

Die Nusselt-Zahl kann durch eine dimensionslose Analyse des Fourier-Gesetzes erhalten werden, da sie gleich dem dimensionslosen Temperaturgradienten an der Oberfläche ist:

${\displaystyle q=-kA\nabla T}$, wobei q die Wärmeübertragungsrate ist , k die konstante Wärmeleitfähigkeit und T die Fluidtemperatur ist .

Tatsächlich, wenn: , und ${\displaystyle \nabla '=L\nabla}$${\displaystyle T'={\frac {T-T_{h}}{T_{h}-T_{c}}}}$

wir kommen an

${\displaystyle -\nabla 'T'={\frac {L}{kA(T_{h}-T_{c})}}q={\frac {hL}{k}}}$

dann definieren wir

${\displaystyle \mathrm {Nu} _{L}={\frac {hL}{k}}}$

so wird die Gleichung

${\displaystyle \mathrm {Nu} _{L}=-\nabla 'T'}$

Durch Integration über die Körperoberfläche:

${\displaystyle {\overline {\mathrm {Nu}}}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S '\!}$,

wo ${\displaystyle S'={\frac {S}{L^{2}}}}$

Empirische Korrelationen

Typischerweise wird für freie Konvektion die durchschnittliche Nusselt-Zahl als Funktion der Rayleigh-Zahl und der Prandtl-Zahl ausgedrückt als:

${\displaystyle\mathrm{Nu} =f(\mathrm{Ra},\mathrm{Pr})}$

Ansonsten ist die Nusselt-Zahl bei erzwungener Konvektion im Allgemeinen eine Funktion der Reynolds-Zahl und der Prandtl-Zahl , oder

${\displaystyle \mathrm{Nu} =f(\mathrm{Re},\mathrm{Pr})}$

Es liegen empirische Korrelationen für verschiedenste Geometrien vor, die die Nusselt-Zahl in den oben genannten Formen ausdrücken.

Freie Konvektion

Freie Konvektion an einer senkrechten Wand

Zitiert als aus Churchill und Chu stammend:

${\displaystyle {\overline {\mathrm {Nu}}}_{L}\ =0.68+{\frac {0.663\,\mathrm {Ra}_{L}^{1/4}}{\left[1 +(0,492/\mathrm{Pr})^{9/16}\,\right]^{4/9}\,}}\quad\mathrm{Ra}_{L}\leq 10^{8}}$

Freie Konvektion durch horizontale Platten

Wenn die charakteristische Länge definiert ist

${\displaystyle L\ ={\frac {A_{s}}{P}}}$

wo ist die Oberfläche der Platte und ihr Umfang. ${\displaystyle \mathrm {A} _{s}}$${\displaystyle P}$

Dann für die Oberseite eines heißen Objekts in einer kälteren Umgebung oder die Unterseite eines kalten Objekts in einer heißeren Umgebung

${\displaystyle {\overline {\mathrm {Nu}}}_{L}\ =0.54\,\mathrm {Ra} _{L}^{1/4}\,\quad 10^{4}\leq\ Mathrm {Ra} _{L}\leq 10^{7}}$

${\displaystyle {\overline {\mathrm {Nu}}}_{L}\ =0,15\,\mathrm {Ra} _{L}^{1/3}\,\quad 10^{7}\leq\ Mathrm {Ra} _{L}\leq 10^{11}}$

Und für die Unterseite eines heißen Objekts in einer kälteren Umgebung oder die Oberseite eines kalten Objekts in einer heißeren Umgebung

${\displaystyle {\overline {\mathrm {Nu}}}_{L}\ =0.52\,\mathrm {Ra} _{L}^{1/5}\,\quad 10^{5}\leq\ Mathrm {Ra} _{L}\leq 10^{10}}$

Erzwungene Konvektion auf flacher Platte

Flache Platte im Laminar Flow

Die lokale Nusselt-Zahl für laminare Strömung über eine ebene Platte im Abstand stromabwärts vom Plattenrand ist gegeben durch ${\displaystyle x}$

${\displaystyle \mathrm {Nu} _{x}\ =0.332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3},(\mathrm { Pr} >0,6)}$

Die durchschnittliche Nusselt-Zahl für laminare Strömung über eine ebene Platte, vom Plattenrand bis zu einer stromabwärtigen Strecke , ist gegeben durch ${\displaystyle x}$

${\displaystyle {\overline {\mathrm {Nu}}}_{x}\ ={2}\cdot 0,332\,\mathrm {Re} _{x}^{1/2}\,\mathrm {Pr} ^{1/3}\ =0,664\,\mathrm{Re}_{x}^{1/2}\,\mathrm{Pr}^{1/3},(\mathrm{Pr} >0,6)}$

Kugel in konvektiver Strömung

Bei einigen Anwendungen, wie der Verdampfung von kugelförmigen Flüssigkeitströpfchen in Luft, wird die folgende Korrelation verwendet:

${\displaystyle \mathrm {Nu} _{D}\ ={2}+0,4\,\mathrm {Re} _{D}^{1/2}\,\mathrm {Pr} ^{1/3}\ ,}$

Erzwungene Konvektion in turbulenter Rohrströmung

Gnielinski-Korrelation

Gnielinskis Korrelation für turbulente Strömung in Rohren:

${\displaystyle \mathrm {Nu} _{D}={\frac {\left(f/8\right)\left(\mathrm {Re}_{D}-1000\right)\mathrm {Pr} }{ 1+12.7(f/8)^{1/2}\left(\mathrm{Pr}^{2/3}-1\right)}}}$

wobei f der Darcy-Reibungsfaktor ist , der entweder aus dem Moody-Diagramm oder für glatte Rohre aus der von Petukhov entwickelten Korrelation erhalten werden kann:

${\displaystyle f=\left(0,79\ln\left(\mathrm {Re}_{D}\right)-1,64\right)^{-2}}$

Die Gnielinski-Korrelation gilt für:

${\displaystyle 0.5\leq \mathrm {Pr} \leq 2000}$

${\displaystyle 3000\leq \mathrm {Re} _{D}\leq 5\times 10^{6}}$

Dittus-Boelter-Gleichung

Die Dittus-Boelter-Gleichung (für turbulente Strömung) ist eine explizite Funktion zur Berechnung der Nusselt-Zahl. Es ist leicht zu lösen, aber weniger genau, wenn eine große Temperaturdifferenz in der Flüssigkeit besteht. Es ist auf glatte Rohre zugeschnitten, daher wird von der Verwendung für raue Rohre (die meisten kommerziellen Anwendungen) abgeraten. Die Dittus-Boelter-Gleichung lautet:

${\displaystyle \mathrm {Nu} _{D}=0,023\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{n}}$

wo:

${\displaystyle D}$ ist der Innendurchmesser des runden Kanals

${\displaystyle \mathrm {Pr}}$ist die Prandtl-Zahl

${\displaystyle n=0,4}$für das Fluid, das erhitzt wird, und für das Fluid, das gekühlt wird.${\displaystyle n=0,3}$

Die Dittus-Boelter-Gleichung gilt für

${\displaystyle 0.6\leq \mathrm {Pr} \leq 160}$

${\displaystyle \mathrm {Re} _{D}\gtrsim 10\,000}$

${\displaystyle {\frac {L}{D}}\gtrsim 10}$

Beispiel Die Dittus-Boelter-Gleichung ist eine gute Näherung, bei der die Temperaturunterschiede zwischen der Hauptflüssigkeit und der Wärmeübertragungsoberfläche minimal sind, wodurch Gleichungskomplexität und iteratives Lösen vermieden werden. Nimmt man Wasser mit einer mittleren Flüssigkeitstemperatur von 20 °C, einer Viskosität von 10,07 × 10 ^–4 Pa·s und einer Wärmeübertragungsoberflächentemperatur von 40 °C (Viskosität 6,96 × 10 ^–4 , kann ein Viskositätskorrekturfaktor für 1,45 erhalten werden) Dieser erhöht sich auf 3,57 bei einer Wärmeübergangsoberflächentemperatur von 100 °C (Viskosität 2,82×10 ⁻⁴ Pa·s), was einen signifikanten Unterschied in der Nusselt-Zahl und dem Wärmeübergangskoeffizienten ausmacht. ${\displaystyle ({\mu}/{\mu_{s}})}$

Sieder-Tate-Korrelation

Die Sieder-Tate-Korrelation für turbulente Strömung ist eine implizite Funktion , da sie das System als nichtlineares Randwertproblem analysiert . Das Sieder-Tate-Ergebnis kann genauer sein, da es die Viskositätsänderung ( und ) aufgrund der Temperaturänderung zwischen der Durchschnittstemperatur des Massenfluids bzw. der Temperatur der Wärmeübertragungsoberfläche berücksichtigt . Die Sieder-Tate-Korrelation wird normalerweise durch einen iterativen Prozess gelöst, da sich der Viskositätsfaktor mit der Änderung der Nusselt-Zahl ändert. ${\displaystyle\mu}$${\displaystyle \mu_{s}}$

${\displaystyle \mathrm {Nu} _{D}=0.027\,\mathrm {Re} _{D}^{4/5}\,\mathrm {Pr} ^{1/3}\left({\frac {\mu}{\mu_{s}}}\right)^{0,14}}$

wo:

${\displaystyle\mu}$ ist die Viskosität des Fluids bei der Temperatur des Volumens des Fluids

${\displaystyle \mu_{s}}$ ist die Fluidviskosität bei der Grenzflächentemperatur des Wärmeübergangs

Die Sieder-Tate-Korrelation gilt für

${\displaystyle 0.7\leq\mathrm {Pr}\leq 16\,700}$

${\displaystyle \mathrm {Re} _{D}\geq 10\,000}$

${\displaystyle {\frac {L}{D}}\gtrsim 10}$

Erzwungene Konvektion bei voll entwickelter laminarer Rohrströmung

Bei voll entwickelter innerer laminarer Strömung tendieren die Nusselt-Zahlen bei langen Rohren zu einem konstanten Wert.

Für internen Fluss:

${\displaystyle \mathrm {Nu} ={\frac {hD_{h}}{k_{f}}}}$

wo:

D _h = Hydraulischer Durchmesser

k _f = Wärmeleitfähigkeit des Fluids

h = konvektiver Wärmedurchgangskoeffizient

Konvektion mit gleichmäßiger Temperatur für Rundrohre

Von Incropera & DeWitt,

${\displaystyle \mathrm {Nu} _{D}=3.66}$

Die OEIS-Sequenz A282581 gibt diesen Wert als . ${\displaystyle \mathrm {Nu} _{D}=3.6567934577632923619...}$

Konvektion mit gleichmäßigem Wärmestrom für Rundrohre

Bei konstantem Oberflächenwärmestrom gilt:

${\displaystyle \mathrm {Nu} _{D}=4.36}$

Siehe auch

• Sherwood-Nummer (Massentransfer-Nusselt-Nummer)
• Churchill-Bernstein-Gleichung
• Biot-Nummer
• Reynolds Nummer
• Konvektive Wärmeübertragung
• Hitzeübertragungskoeffizient
• Wärmeleitfähigkeit

Verweise

Externe Links

• Einfache Ableitung der Nusselt-Zahl aus dem Newtonschen Kühlgesetz (Zugriff am 23. September 2009)