Teilung einer Menge - Partition of a set

Ein Satz Briefmarken, der in Bündel unterteilt ist: Keine Briefmarke ist in zwei Bündeln, kein Bündel ist leer und jede Briefmarke befindet sich in einem Bündel.

Die 52 Partitionen eines Sets mit 5 Elementen. Ein farbiger Bereich zeigt eine Teilmenge von X an, die ein Mitglied der umschließenden Partition bildet. Ungefärbte Punkte weisen auf Einzelelement-Untermengen hin. Die erste gezeigte Partition enthält fünf Einzelelement-Untermengen; die letzte Partition enthält eine Teilmenge mit fünf Elementen.

Die traditionellen japanischen Symbole für die 54 Kapitel der Tale of Genji basieren auf den 52 Arten der Unterteilung von fünf Elementen (die beiden roten Symbole stehen für dieselbe Unterteilung, und das grüne Symbol wird hinzugefügt, um 54 zu erreichen).

In der Mathematik ist eine Partition einer Menge eine Gruppierung ihrer Elemente in nichtleere Teilmengen , so dass jedes Element in genau einer Teilmenge enthalten ist.

Jede Äquivalenzrelation auf einer Menge definiert eine Partition dieser Menge, und jede Partition definiert eine Äquivalenzrelation. Eine Menge, die mit einer Äquivalenzrelation oder einer Partition ausgestattet ist, wird manchmal Setoid genannt , typischerweise in der Typentheorie und der Beweistheorie .

Definition und Notation

Eine Partition einer Menge X ist eine Menge nichtleerer Teilmengen von X, so dass jedes Element x in X in genau einer dieser Teilmengen liegt (dh X ist eine disjunkte Vereinigung der Teilmengen).

Äquivalent ist eine Menge von Mengen P genau dann eine Partition von X, wenn alle der folgenden Bedingungen erfüllt sind:

• Die Familie P enthält nicht die leere Menge (also ).${\displaystyle \emptyset\notin P}$
• Die Vereinigung der Mengen in P ist gleich X (also ). Die Mengen in P sollen X erschöpfen oder abdecken . Siehe auch kollektiv erschöpfende Ereignisse und Cover (Topologie) .${\displaystyle \textstyle \bigcup _{A\in P}A=X}$
• Der Schnittpunkt zweier verschiedener Mengen in P ist leer (also ). Die Elemente von P heißen paarweise disjunkt .${\displaystyle (\forall A,B\in P)\;A\neq B\implies A\cap B=\emptyset }$

Die Mengen in P werden Blöcke , Teile oder Zellen der Partition genannt. Wenn dann stellen wir die Zelle dar, die a enthält durch . Das heißt, ist Notation für die Zelle in P , die enthält ein . ${\displaystyle a\in X}$${\displaystyle [a]}$${\displaystyle [a]}$

Jede Partition P kann mit einer Äquivalenzrelation auf identifiziert wird X , nämlich die Beziehung , so dass für jede wir haben , wenn und nur wenn (äquivalent, wenn und nur wenn ). Die Notation evoziert die Idee, dass die Äquivalenzrelation aus der Partition konstruiert werden kann. Umgekehrt kann jede Äquivalenzrelation mit einer Partition identifiziert werden. Aus diesem Grund wird manchmal informell gesagt, dass "eine Äquivalenzrelation dasselbe ist wie eine Partition". Wenn P die Partition ist, die mit einer gegebenen Äquivalenzrelation identifiziert wird , dann schreiben einige Autoren . Diese Notation weist auf die Idee hin, dass die Partition die Menge X ist, die in Zellen unterteilt ist. Die Notation evoziert auch die Idee, dass man aus der Äquivalenzrelation die Partition konstruieren kann. ${\displaystyle \sim_{P}}$${\displaystyle a,b\in X}$${\displaystyle a\sim_{P}b}$${\displaystyle a\in [b]}$${\displaystyle b\in [a]}$${\displaystyle \sim_{P}}$${\displaystyle\sim}$${\displaystyle P=X/\sim}$

Der Rang von P ist | X | − | P | Wenn X ist endlich .

Beispiele

• Die leere Menge hat genau eine Partition, nämlich . (Hinweis: Dies ist die Partition, kein Mitglied der Partition.)${\displaystyle \emptyset}$${\displaystyle \emptyset}$
• Für jede nichtleere Menge X ist P = { X } eine Partition von X , die triviale Partition genannt wird .
  • Insbesondere hat jede Singleton-Menge { x } genau eine Partition, nämlich { { x } }.
• Für jede nichtleere echte Teilmenge A einer Menge U bildet die Menge A zusammen mit ihrem Komplement eine Partition von U , nämlich { A , U ∖ A }.
• Die Menge {1, 2, 3} hat diese fünf Partitionen (eine Partition pro Element):
  • { {1}, {2}, {3} }, manchmal geschrieben 1 | 2 | 3.
  • { {1, 2}, {3} } oder 1 2 | 3.
  • { {1, 3}, {2} } oder 1 3 | 2.
  • { {1}, {2, 3} } oder 1 | 2 3.
  • { {1, 2, 3} } oder 123 (in Kontexten, in denen es keine Verwechslung mit der Zahl gibt).
• Das Folgende sind keine Partitionen von {1, 2, 3}:
  • { {}, {1, 3}, {2} } ist keine Partition (einer Menge), da eines ihrer Elemente die leere Menge ist .
  • { {1, 2}, {2, 3} } ist keine Partition (einer Menge), da das Element 2 in mehr als einem Block enthalten ist.
  • { {1}, {2} } ist keine Partition von {1, 2, 3}, da keiner seiner Blöcke 3 enthält; es ist jedoch eine Partition von {1, 2}.

Partitionen und Äquivalenzrelationen

Für jede Äquivalenzrelation auf einer Menge X ist die Menge ihrer Äquivalenzklassen eine Partition von X . Umgekehrt können wir aus jeder Partition P von X eine Äquivalenzrelation auf X definieren, indem wir x ~ y genau dann setzen, wenn x und y in P im gleichen Teil liegen . Somit sind die Begriffe Äquivalenzrelation und Partition im Wesentlichen äquivalent.

Das Auswahlaxiom garantiert für jede Partition einer Menge X die Existenz einer Teilmenge von X, die genau ein Element aus jedem Teil der Partition enthält. Dies impliziert, dass man bei einer Äquivalenzrelation auf einer Menge aus jeder Äquivalenzklasse ein kanonisches repräsentatives Element auswählen kann .

Verfeinerung der Partitionen

Partitionen einer 4er-Menge, geordnet nach Verfeinerung

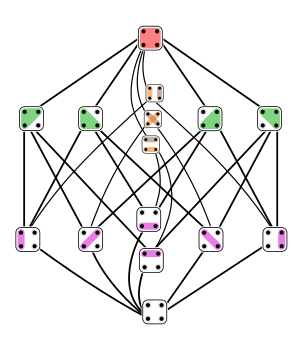
Eine Trennwand α einen Satz X ist eine Verfeinerung einer Partition ρ von X -und wir sagen , dass α ist feiner als ρ und ρ ist gröber als α -wenn jedes Element von α eine Teilmenge von einem Elemente von ist ρ . Informell bedeutet dies, dass α eine weitere Fragmentierung von ρ ist . In diesem Fall wird geschrieben, dass α ≤ ρ .

Diese Feiner-als- Beziehung auf der Menge von Partitionen von X ist eine Teilordnung (also die Notation "≤" ist angemessen). Jede Menge von Elementen hat eine kleinste obere Schranke und eine größte untere Schranke , so dass sie ein Gitter bildet , und genauer gesagt (für Partitionen einer endlichen Menge) ist sie ein geometrisches Gitter . Das Teilungsgitter einer 4-Element-Menge hat 15 Elemente und ist im Hasse-Diagramm links dargestellt.

Basierend auf dem Kryptomorphismus zwischen geometrischen Gittern und Matroiden entspricht dieses Partitionsgitter einer endlichen Menge einem Matroid, bei dem die Basismenge des Matroids aus den Atomen des Gitters besteht, nämlich den Partitionen mit Singleton-Mengen und einem Zweielement einstellen. Diese atomaren Partitionen entsprechen eins zu eins den Kanten eines vollständigen Graphen . Der matroide Abschluss einer Menge atomarer Partitionen ist die feinste gemeinsame Vergröberung von allen; graphentheoretisch ist es die Zerlegung der Ecken des vollständigen Graphen in die zusammenhängenden Komponenten des Teilgraphen, der durch die gegebene Kantenmenge gebildet wird. Auf diese Weise entspricht das Gitter der Partitionen dem Gitter der Ebenen des grafischen Matroids des vollständigen Graphen. ${\displaystyle n-2}$

Ein weiteres Beispiel illustriert die Verfeinerung von Partitionen aus der Perspektive von Äquivalenzrelationen. Wenn D der Kartensatz in einem standardmäßigen 52-Karten-Deck ist, hat die gleiche Farbe-wie- Beziehung auf D – die als ~ _{C bezeichnet werden kann} – zwei Äquivalenzklassen: die Sätze {rote Karten} und {schwarze Karten}. Die 2-teilige Partition, die ~ _C entspricht, hat eine Verfeinerung, die die gleiche-Anzug-wie- Relation ~ _S liefert , die die vier Äquivalenzklassen {Pik}, {Rauten}, {Herzen} und {Keulen} hat.

Nicht kreuzende Partitionen

Eine Zerlegung der Menge N = {1, 2, ..., n } mit entsprechender Äquivalenzrelation ~ ist nicht kreuzend, wenn sie folgende Eigenschaft hat: Wenn vier Elemente a , b , c und d von N mit a < b < c < d erfüllen a ~ c und b ~ d , dann a ~ b ~ c ~ d . Der Name kommt von der folgenden äquivalenten Definition: Stellen Sie sich die Elemente 1, 2, ..., n von N als die n Ecken eines regulären n -Ecks (im Gegenuhrzeigersinn) vor. Eine Partition kann dann visualisiert werden, indem jeder Block als Polygon gezeichnet wird (dessen Scheitelpunkte die Elemente des Blocks sind). Die Partition ist dann genau dann nicht kreuzend, wenn sich diese Polygone nicht schneiden.

Das Gitter der sich nicht kreuzenden Partitionen einer endlichen Menge hat in letzter Zeit wegen seiner Rolle in der Theorie der freien Wahrscheinlichkeit an Bedeutung gewonnen. Diese bilden eine Teilmenge des Gitters aller Partitionen, aber kein Untergitter, da die Verknüpfungsoperationen der beiden Gitter nicht übereinstimmen.

Zählen von Partitionen

Die Gesamtzahl der Partitionen einer n- elementigen Menge ist die Bell-Zahl B _n . Die ersten mehreren Glockenzahlen sind B ₀ = 1, B ₁ = 1, B ₂ = 2, B ₃ = 5, B ₄ = 15, B ₅ = 52 und B ₆ = 203 (Sequenz A000110 im OEIS ). Glockenzahlen erfüllen die Rekursion

${\displaystyle B_{n+1}=\sum_{k=0}^{n}{n \choose k}B_{k}}$

und haben die exponentielle erzeugende Funktion

${\displaystyle \sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}z^{n}=e^{e^{z}-1}.}$

Konstruktion des Glockendreiecks

Die Bell-Zahlen können auch mit dem Bell-Dreieck berechnet werden, bei dem der erste Wert in jeder Reihe vom Ende der vorherigen Reihe kopiert wird und die nachfolgenden Werte durch Addieren von zwei Zahlen berechnet werden, die Zahl links und die Zahl oben links von der Stelle. Die Glockenzahlen werden auf beiden Seiten dieses Dreiecks wiederholt. Die Zahlen innerhalb des Dreiecks zählen Partitionen, in denen ein gegebenes Element das größte Singleton ist .

Die Anzahl der Partitionen einer n- elementigen Menge in genau k nicht-leere Teile ist die Stirling-Zahl zweiter Art S ( n , k ).

Die Anzahl der sich nicht kreuzenden Partitionen einer n- elementigen Menge ist die katalanische Zahl C _n , gegeben durch

${\displaystyle C_{n}={1 \over n+1}{2n \choose n}.}$

Siehe auch

• Genaue Abdeckung
• Blockdesign
• Clusteranalyse
• Schwache Ordnung (geordnete Satzpartition)
• Partielle Äquivalenzrelation
• Partitionsverfeinerung
• Liste der Partitionsthemen
• Laminierung (Topologie)
• Reimschemata nach Satzpartition

Anmerkungen

Verweise

• Brualdi, Richard A. (2004). Einführende Kombinatorik (4. Aufl.). Pearson Prentice Hall. ISBN 0-13-100119-1.
• Scheiter, Eric (1997). Handbuch der Analysis und ihrer Grundlagen . Akademische Presse. ISBN 0-12-622760-8.