Reaktions-Diffusionssystem - Reaction–diffusion system

Eine Simulation zweier virtueller Chemikalien, die auf einem Torus reagieren und diffundieren, unter Verwendung des Gray-Scott-Modells

Reaktions-Diffusions-Systeme sind mathematische Modelle, die mehreren physikalischen Phänomenen entsprechen. Am gebräuchlichsten ist die räumliche und zeitliche Änderung der Konzentration eines oder mehrerer chemischer Stoffe: lokale chemische Reaktionen, bei denen die Stoffe ineinander umgewandelt werden, und Diffusion, bei der sich die Stoffe über eine Fläche im Raum ausbreiten.

Reaktions-Diffusions-Systeme werden natürlicherweise in der Chemie verwendet . Das System kann aber auch dynamische Prozesse nicht-chemischer Natur beschreiben. Beispiele finden sich in Biologie , Geologie und Physik (Neutronendiffusionstheorie) und Ökologie . Mathematisch haben Reaktions-Diffusions-Systeme die Form halblinearer parabolischer partieller Differentialgleichungen . Sie können in der allgemeinen Form dargestellt werden

\partial_{t}{\boldsymbol {q}}={\underline {\underline {\boldsymbol {D}}}}\,\nabla ^{2}{\boldsymbol {q}}+{\ Fettsymbol {R}}({\boldsymbol {q}}),

wobei $q (x, t)$ die unbekannte Vektorfunktion darstellt, $D$ eine Diagonalmatrix von Diffusionskoeffizienten ist und $R$ alle lokalen Reaktionen berücksichtigt. Die Lösungen von Reaktions-Diffusions-Gleichungen zeigen ein breites Spektrum an Verhalten, einschließlich der Bildung von Wanderwellen und wellenähnlichen Phänomenen sowie anderer selbstorganisierter Muster wie Streifen, Sechsecke oder komplizierterer Strukturen wie dissipativen Solitonen . Solche Muster wurden „ Turing-Muster “ genannt. Jede Funktion, für die eine Reaktions-Diffusions-Differentialgleichung gilt, repräsentiert tatsächlich eine Konzentrationsvariable .

Einkomponentige Reaktions-Diffusions-Gleichungen

Die einfachste Reaktions-Diffusions-Gleichung liegt in einer räumlichen Dimension in ebener Geometrie vor,

\partial_{t}u=D\partial_{x}^{2}u+R(u),

wird auch als Kolmogorov-Petrovsky-Piskunov-Gleichung bezeichnet . Verschwindet der Reaktionsterm, so stellt die Gleichung einen reinen Diffusionsprozess dar. Die entsprechende Gleichung ist das zweite Fick-Gesetz . Die Wahl $R (u) = u (1 - u)$ ergibt die Fisher-Gleichung , die ursprünglich zur Beschreibung der Ausbreitung biologischer Populationen verwendet wurde , die Newell-Whitehead-Segel-Gleichung mit $R (u) = u (1 - u 2)$ zur Beschreibung Rayleigh-Bénard-Konvektion , die allgemeinere Zeldovich- Gleichung mit $R (u) = u (1 - u)(u - α)$ und $0 < α < 1$ , die in der Verbrennungstheorie auftritt, und ihr spezieller entarteter Fall mit $R (u) = u 2 - u 3$ , die manchmal auch als Zeldovich-Gleichung bezeichnet wird.

Die Dynamik von Einkomponentensystemen unterliegt gewissen Einschränkungen, da die Evolutionsgleichung auch in der Variationsform geschrieben werden kann

\partial_{t}u=-{\frac {\delta {\mathfrak{L}}}{\delta u}}

und beschreibt damit eine permanente Abnahme der durch das Funktional gegebenen "freien Energie" ${\mathfrak {L}}$

{\mathfrak{L}}=\int_{-\infty}^{\infty}\left[{\tfrac{D}{2}}\left(\partial_{x}u\right) ^{2}-V(u)\right]\,{\text{d}}x

mit einem Potential $V (u)$ , so dass $R ( u ) =.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} d V ( u )/d u.$

Eine Wanderwellenfront-Lösung für die Fisher-Gleichung.

In Systemen mit mehr als einer stationären homogenen Lösung wird eine typische Lösung durch Wanderfronten gegeben, die die homogenen Zustände verbinden. Diese Lösungen bewegen sich mit konstanter Geschwindigkeit ohne ihre Form zu ändern und haben die Form $u (x, t) = û (ξ)$ mit $ξ = x - ct$ , wobei $c$ die Geschwindigkeit der Wanderwelle ist. Beachten Sie, dass Wanderwellen zwar allgemein stabile Strukturen sind, aber alle nicht monotonen stationären Lösungen (zB lokalisierte Domänen bestehend aus einem Front-Antifront-Paar) instabil sind. Für $c = 0$ gibt es einen einfachen Beweis für diese Aussage: Wenn $u 0 (x)$ eine stationäre Lösung und $u = u 0 (x) + ũ (x, t)$ eine infinitesimal gestörte Lösung ist, liefert die lineare Stabilitätsanalyse die Gleichung

\partial_{t}{\tilde{u}}=D\partial_{x}^{2}{\tilde{u}}-U(x){\tilde{u}},\qquad U(x)=-R^{\prime}(u){\Big |}_{u=u_{0}(x)}.

Mit dem Ansatz $ũ = ψ (x)exp(- λt) erhalten$ wir das Eigenwertproblem

{\hat{H}}\psi =\lambda\psi,\qquad{\hat{H}}=-D\partial_{x}^{2}+U(x),

vom Schrödinger-Typ, wobei negative Eigenwerte zur Instabilität der Lösung führen. Aufgrund der Translationsinvarianz ist $ψ = \partial x u 0 (x)$ eine neutrale Eigenfunktion mit dem Eigenwert $λ = 0$ , und alle anderen Eigenfunktionen lassen sich nach steigender Knotenzahl sortieren, wobei der Betrag des entsprechenden reellen Eigenwerts monoton mit dem Anzahl der Nullen. Die Eigenfunktion $ψ = \partial x u 0 (x)$ sollte mindestens eine Nullstelle haben, und für eine nicht monotone stationäre Lösung kann der zugehörige Eigenwert $λ = 0$ nicht der kleinste sein, was Instabilität impliziert.

Um die Geschwindigkeit $c$ einer sich bewegenden Front zu bestimmen , kann man zu einem bewegten Koordinatensystem gehen und stationäre Lösungen betrachten:

D\partial_{\xi}^{2}{\hat{u}}(\xi)+c\partial_{\xi}{\hat{u}}(\xi)+R({ \hat{u}}(\xi))=0.

Diese Gleichung hat ein schönes mechanisches Analogon als die Bewegung einer Masse $D$ mit Position $û$ im Verlauf der "Zeit" $ξ$ unter der Kraft $R$ mit dem Dämpfungskoeffizienten c, was einen recht anschaulichen Zugang zur Konstruktion verschiedener Lösungstypen ermöglicht und die Bestimmung von $c$ .

Beim Übergang von einer zu mehreren Raumdimensionen können noch eine Reihe von Aussagen aus eindimensionalen Systemen angewendet werden. Planare oder gekrümmte Wellenfronten sind typische Strukturen, und ein neuer Effekt tritt auf, wenn die lokale Geschwindigkeit einer gekrümmten Front vom lokalen Krümmungsradius abhängt (dies kann durch die Polarkoordinaten gesehen werden ). Dieses Phänomen führt zur sogenannten krümmungsbedingten Instabilität.

Zweikomponenten-Reaktions-Diffusions-Gleichungen

Zweikomponentensysteme ermöglichen eine viel größere Bandbreite möglicher Phänomene als ihre einkomponentigen Gegenstücke. Eine wichtige Idee, die zuerst von Alan Turing vorgeschlagen wurde, ist, dass ein im lokalen System stabiler Zustand in Gegenwart von Diffusion instabil werden kann .

Eine lineare Stabilitätsanalyse zeigt jedoch, dass bei der Linearisierung des allgemeinen Zweikomponentensystems

{\begin{pmatrix}\partial_{t}u\\\partial_{t}v\end{pmatrix}}={\begin{pmatrix}D_{u}&0\\0&D_{v}\ end{pmatrix}}{\begin{pmatrix}\partial_{xx}u\\\partial_{xx}v\end{pmatrix}}+{\begin{pmatrix}F(u,v)\\G( u,v)\end{pmatrix}}

eine ebene Welle Perturbation

{\tilde {\boldsymbol {q}}}_{\boldsymbol {k}}({\boldsymbol {x}},t)={\begin{pmatrix}{\tilde {u}}(t) \\{\tilde{v}}(t)\end{pmatrix}}e^{i{\boldsymbol {k}}\cdot {\boldsymbol {x}}}

der stationären homogenen Lösung erfüllt

{\begin{pmatrix}\partial_{t}{\tilde {u}}_{\boldsymbol {k}}(t)\\\partial_{t}{\tilde {v}}_{ \boldsymbol {k}}(t)\end{pmatrix}}=-k^{2}{\begin{pmatrix}D_{u}{\tilde {u}}_{\boldsymbol {k}}(t) \\D_{v}{\tilde{v}}_{\boldsymbol {k}}(t)\end{pmatrix}}+{\boldsymbol {R}}^{\prime }{\begin{pmatrix}{ \tilde{u}}_{\boldsymbol{k}}(t)\\{\tilde{v}}_{\boldsymbol{k}}(t)\end{pmatrix}}.

Turings Idee lässt sich nur in vier Äquivalenzklassen von Systemen realisieren, die durch die Vorzeichen des Jacobi- $R'$ der Reaktionsfunktion gekennzeichnet sind. Insbesondere wenn ein endlicher Wellenvektor $k$ der instabilste sein soll, muss der Jacobi- Vektor die Vorzeichen

{\begin{pmatrix}+&-\\+&-\end{pmatrix}},\quad {\begin{pmatrix}+&+\\-&-\end{pmatrix}},\quad { \begin{pmatrix}-&+\\-&+\end{pmatrix}},\quad {\begin{pmatrix}-&-\\+&+\end{pmatrix}}.

Diese Systemklasse wird nach ihrem ersten Vertreter als Aktivator-Inhibitor-System bezeichnet : Nahe dem Grundzustand stimuliert eine Komponente die Produktion beider Komponenten, während die andere deren Wachstum hemmt. Ihr prominentester Vertreter ist die FitzHugh-Nagumo-Gleichung

{\begin{ausgerichtet}\partial_{t}u&=d_{u}^{2}\,\nabla ^{2}u+f(u)-\sigma v,\\\tau \partial _{t}v&=d_{v}^{2}\,\nabla ^{2}v+uv\end{ausgerichtet}}

mit $f$ $($ $u$ $) =$ $λu$ $-$ $u$ $3$ $-$ $κ$ was beschreibt, wie ein Aktionspotential durch einen Nerv wandert. Hier $d$ $u$ $,$ $d$ $v$ $,$ $τ$ $,$ $σ$ und $λ$ positive Konstanten sind .

Wenn ein Aktivator-Inhibitor-System eine Parameteränderung erfährt, kann man von Bedingungen, unter denen ein homogener Grundzustand stabil ist, zu Bedingungen übergehen, unter denen er linear instabil ist. Die entsprechende Bifurkation kann entweder eine Hopf-Bifurkation in einen global oszillierenden homogenen Zustand mit einer dominanten Wellenzahl $k = 0$ oder eine Turing-Bifurkation in einen global gemusterten Zustand mit einer dominanten endlichen Wellenzahl sein. Letzteres in zwei Raumdimensionen führt typischerweise zu Streifen- oder Sechseckmustern.

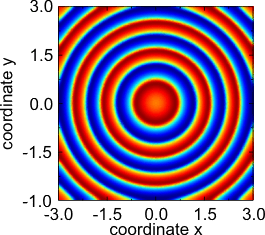
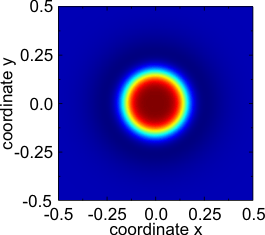
Subkritische Turing-Verzweigung: Bildung eines hexagonalen Musters aus verrauschten Anfangsbedingungen im obigen Zweikomponenten-Reaktions-Diffusions-System vom Fitzhugh-Nagumo-Typ.
Verrauschte Anfangsbedingungen bei t = 0.
Zustand des Systems bei t = 10.
Fast konvergierter Zustand bei t = 100.

Für das Fitzhugh-Nagumo-Beispiel sind die neutralen Stabilitätskurven, die die Grenze des linear stabilen Bereichs für die Turing- und Hopf-Bifurkation markieren, gegeben durch

{\begin{ausgerichtet}q_{\text{n}}^{H}(k):&{}\quad {\frac {1}{\tau}}+\left(d_{u}^ {2}+{\frac{1}{\tau}}d_{v}^{2}\right)k^{2}&=f^{\prime}(u_{h}),\\[6pt ]q_{\text{n}}^{T}(k):&{}\quad {\frac {\kappa }{1+d_{v}^{2}k^{2}}}+d_{ u}^{2}k^{2}&=f^{\prime}(u_{h}).\end{ausgerichtet}}

Wenn die Bifurkation unterkritisch ist, können oft lokalisierte Strukturen ( dissipative Solitonen ) in der Hystereseregion beobachtet werden, in der das Muster mit dem Grundzustand koexistiert. Andere häufig anzutreffende Strukturen umfassen Pulsfolgen (auch als periodische Wanderwellen bekannt ), Spiralwellen und Zielmuster. Diese drei Lösungstypen sind auch generische Merkmale von Zwei-(oder Mehr-)Komponenten-Reaktions-Diffusions-Gleichungen, in denen die lokale Dynamik einen stabilen Grenzzyklus hat

Andere Muster, die in dem obigen Zweikomponenten-Reaktions-Diffusions-System vom Fitzhugh-Nagumo-Typ gefunden wurden.
Rotierende Spirale.
Zielmuster.
Stationärer lokalisierter Puls (dissipatives Soliton).

Drei- und Mehrkomponenten-Reaktions-Diffusions-Gleichungen

Für eine Vielzahl von Systemen wurden Reaktions-Diffusions-Gleichungen mit mehr als zwei Komponenten vorgeschlagen, zB die Belousov-Zhabotinsky-Reaktion , für Blutgerinnungs- oder planare Gasentladungssysteme .

Es ist bekannt, dass Systeme mit mehr Komponenten eine Vielzahl von Phänomenen ermöglichen, die in Systemen mit einer oder zwei Komponenten nicht möglich sind (zB stabile Laufpulse in mehr als einer räumlichen Dimension ohne globale Rückkopplung). Eine Einführung und ein systematischer Überblick über die möglichen Phänomene in Abhängigkeit von den Eigenschaften des zugrunde liegenden Systems findet sich in.

Anwendungen und Universalität

In jüngster Zeit haben Reaktions-Diffusions-Systeme als Prototypmodell für die Musterbildung großes Interesse geweckt . Die oben genannten Muster (Fronten, Spiralen, Targets, Sechsecke, Streifen und dissipative Solitonen) finden sich trotz großer Diskrepanzen zB in den lokalen Reaktionstermen in verschiedenen Typen von Reaktions-Diffusions-Systemen. Es wurde auch argumentiert, dass Reaktions-Diffusions-Prozesse eine wesentliche Grundlage für Prozesse im Zusammenhang mit der Morphogenese in der Biologie sind und sogar mit Tierfellen und Hautpigmentierung zusammenhängen können. Andere Anwendungen von Reaktions-Diffusions-Gleichungen umfassen ökologische Invasionen, Ausbreitung von Epidemien, Tumorwachstum und Wundheilung. Ein weiterer Grund für das Interesse an Reaktions-Diffusions-Systemen besteht darin, dass es sich zwar um nichtlineare partielle Differentialgleichungen handelt, es jedoch oft Möglichkeiten für eine analytische Behandlung gibt.

Experimente

Gut kontrollierbare Experimente in chemischen Reaktions-Diffusions-Systemen wurden bisher auf drei Arten realisiert. Zunächst können Gelreaktoren oder gefüllte Kapillarröhrchen verwendet werden. Zweitens wurden Temperaturpulse auf katalytischen Oberflächen untersucht. Drittens wird die Ausbreitung von Nervenimpulsen mit Reaktions-Diffusions-Systemen modelliert.

Abgesehen von diesen generischen Beispielen hat sich gezeigt, dass elektrische Transportsysteme wie Plasmen oder Halbleiter unter geeigneten Umständen in einem Reaktions-Diffusions-Ansatz beschrieben werden können. Für diese Systeme wurden verschiedene Experimente zur Musterbildung durchgeführt.

Numerische Behandlungen

Ein Reaktions-Diffusions-System kann mit Methoden der numerischen Mathematik gelöst werden . In der Forschungsliteratur gibt es mehrere numerische Behandlungen. Auch für komplexe Geometrien werden numerische Lösungsverfahren vorgeschlagen. Bis ins kleinste Detail werden Reaktions-Diffusions-Systeme mit partikelbasierten Simulationstools wie SRSim oder ReaDDy beschrieben, die beispielsweise reversible Wechselwirkungs-Partikel-Reaktionsdynamiken verwenden.

Siehe auch

Beispiele

Verweise

Externe Links

Reaktion-Diffusion durch das Gray-Scott-Modell: Pearsons Parametrisierung eine visuelle Karte des Parameterraums der Gray-Scott-Reaktionsdiffusion.
Eine Dissertation über Reaktions-Diffusions-Muster mit einem Überblick über das Gebiet

Languages

In other projects