Turm von Hanoi - Tower of Hanoi

Ein Modellset des Turms von Hanoi (mit 8 Scheiben)

Eine animierte Lösung des Rätsels Turm von Hanoi für T (4, 3)

Interaktive Ausstellung des Turms von Hanoi im Universum Museum in Mexiko-Stadt

Der Turm von Hanoi (auch Das Problem des Benares-Tempels oder Turm von Brahma oder Lucas' Turm genannt und manchmal als Türme oder einfach als Pyramidenpuzzle bezeichnet ) ist ein mathematisches Spiel oder Puzzle, das aus drei Stäben und einer Reihe von Scheiben mit verschiedenen Durchmessern besteht. die auf jede Stange gleiten kann. Das Puzzle beginnt damit, dass die Scheiben nach abnehmender Größe auf einem Stab gestapelt sind, die kleinste oben, wodurch sich eine konische Form annähert. Das Ziel des Puzzles besteht darin, den gesamten Stapel bis zum letzten Stab zu bewegen, wobei die folgenden Regeln beachtet werden:

1. Es kann immer nur eine Festplatte gleichzeitig verschoben werden.
2. Jeder Zug besteht darin, die obere Scheibe von einem der Stapel zu nehmen und auf einen anderen Stapel oder auf einen leeren Stab zu legen.
3. Keine Diskette darf auf eine kleinere Diskette gelegt werden.

Mit 3 Scheiben kann das Puzzle in 7 Zügen gelöst werden. Die Mindestanzahl an Zügen, die zum Lösen eines Turms von Hanoi-Rätsel erforderlich sind, beträgt 2 ⁿ − 1, wobei n die Anzahl der Scheiben ist.

Ursprünge

Das Puzzle wurde 1883 von dem französischen Mathematiker Édouard Lucas in den Westen eingeführt. Zahlreiche Mythen über die antike und mystische Natur des Puzzles tauchten fast sofort auf, darunter einer über einen indischen Tempel in Kashi Vishwanath , der einen großen Raum mit drei von der Zeit getragenen Beiträge darin, umgeben von 64 goldenen Scheiben. Seit dieser Zeit bewegen Brahmanenpriester diese Scheiben gemäß den unveränderlichen Regeln von Brahma, indem sie den Befehl einer alten Prophezeiung ausführen . Das Puzzle wird daher auch als Turm von Brahma bezeichnet . Der Legende nach endet die Welt, wenn der letzte Zug des Puzzles abgeschlossen ist.

Wenn die Legende wahr wäre und die Priester in der Lage wären, Scheiben mit einer Geschwindigkeit von einer pro Sekunde und mit der kleinsten Anzahl von Bewegungen zu bewegen, würden sie 2 ⁶⁴  − 1 Sekunden oder ungefähr 585 Milliarden Jahre brauchen, um sie fertig zu stellen, was ungefähr ist 42 mal das aktuelle Alter des Universums.

Es gibt viele Variationen dieser Legende. Zum Beispiel ist in manchen Erzählungen der Tempel ein Kloster und die Priester sind Mönche . Der Tempel oder das Kloster kann sich an verschiedenen Orten befinden, einschließlich Hanoi , und kann mit jeder Religion in Verbindung gebracht werden . In einigen Versionen werden andere Elemente eingeführt, wie zum Beispiel die Tatsache, dass der Turm am Anfang der Welt entstand oder dass die Priester oder Mönche nur einen Zug pro Tag machen dürfen.

Lösung

Das Puzzle kann mit beliebig vielen Scheiben gespielt werden, obwohl viele Spielzeugversionen etwa 7 bis 9 davon haben. Die minimale Anzahl an Zügen, die zum Lösen eines Turms von Hanoi-Rätsel erforderlich sind, beträgt 2 ⁿ − 1 , wobei n die Anzahl der Scheiben ist. Dies ist genau die n- ^te Mersenne-Zahl ohne Primalitätsanforderungen.

Iterative Lösung

Animation eines iterativen Algorithmus zur Lösung des 6-Disk-Problems

Eine einfache Lösung für das Spielzeugpuzzle besteht darin, die Bewegungen zwischen dem kleinsten Teil und einem nicht-kleinsten Teil abzuwechseln. Beim Verschieben des kleinsten Teils immer in die gleiche Richtung auf die nächste Position verschieben (nach rechts bei gerader Startzahl, nach links bei ungerader Startzahl). Wenn in der gewählten Richtung keine Turmposition vorhanden ist, bewegen Sie das Teil zum gegenüberliegenden Ende, bewegen Sie sich dann jedoch weiter in die richtige Richtung. Wenn Sie zum Beispiel mit drei Stücken begonnen haben, würden Sie das kleinste Stück zum gegenüberliegenden Ende verschieben und danach in die linke Richtung weiterfahren. Wenn die nicht-kleinste Figur an der Reihe ist, gibt es nur einen legalen Zug. Dadurch wird das Puzzle in den wenigsten Zügen vervollständigt.

Einfachere Aussage der iterativen Lösung

Für eine gerade Anzahl von Festplatten:

• Machen Sie die legale Bewegung zwischen den Spielsteinen A und B (in beide Richtungen),
• Machen Sie die legale Bewegung zwischen den Spielsteinen A und C (in beide Richtungen),
• Machen Sie die legale Bewegung zwischen den Spielsteinen B und C (in beide Richtungen),
• wiederholen, bis es fertig ist.

Für eine ungerade Anzahl von Festplatten:

• Machen Sie die legale Bewegung zwischen den Spielsteinen A und C (in beide Richtungen),
• Machen Sie die legale Bewegung zwischen den Spielsteinen A und B (in beide Richtungen),
• Machen Sie die legale Bewegung zwischen den Spielsteinen B und C (in beide Richtungen),
• wiederholen, bis es fertig ist.

Es werden jeweils insgesamt 2 ⁿ − 1 Züge ausgeführt.

Äquivalente iterative Lösung

Eine andere Möglichkeit, die einzigartige optimale iterative Lösung zu generieren:

Nummerieren Sie die Festplatten von 1 bis n (vom größten zum kleinsten).

• Wenn n ungerade ist, erfolgt der erste Zug von Peg A nach Peg C.
• Wenn n gerade ist, erfolgt der erste Zug von Peg A nach Peg B.

Fügen Sie nun diese Einschränkungen hinzu:

• Keine ungerade Scheibe darf direkt auf eine ungerade Scheibe gelegt werden.
• Keine gerade Scheibe darf direkt auf eine gerade Scheibe gelegt werden.
• Manchmal gibt es zwei mögliche Stifte: einer hat Festplatten und der andere ist leer. Legen Sie die Diskette auf den nicht leeren Stift.
• Verschieben Sie eine Diskette nie zweimal hintereinander.

In Anbetracht dieser Einschränkungen nach dem ersten Zug gibt es in jedem weiteren Zug nur einen legalen Zug.

Die Abfolge dieser einzigartigen Bewegungen ist eine optimale Lösung des Problems, das der oben beschriebenen iterativen Lösung entspricht.

Rekursive Lösung

Illustration einer rekursiven Lösung für das Rätsel Türme von Hanoi mit 4 Scheiben

Der Schlüssel zur rekursiven Lösung eines Problems besteht darin, zu erkennen, dass es in eine Sammlung kleinerer Teilprobleme zerlegt werden kann, für die jeweils dasselbe allgemeine Lösungsverfahren gilt, das wir suchen , und die Gesamtlösung wird dann in einigen einfachen Weg von den Lösungen dieser Teilprobleme. Jedes dieser erzeugten Unterprobleme ist "kleiner" und garantiert, dass der/die Basisfall(e) schließlich erreicht wird/werden. Von dort für die Türme von Hanoi:

• beschrifte die Stifte A, B, C,
• sei n die Gesamtzahl der Festplatten,
• Nummeriere die Platten von 1 (kleinste, oberste) bis n (größte, unterste).

Angenommen, alle n Platten sind in gültiger Anordnung auf die Stifte verteilt; unter der Annahme, dass es m oberste Festplatten auf einem Quell- Peg gibt und alle übrigen Festplatten größer als m sind , sodass sie sicher ignoriert werden können; um m Festplatten von einem Quell-Peg zu einem Ziel- Peg zu verschieben, indem ein Ersatz- Peg verwendet wird, ohne die Regeln zu verletzen:

1. Verschieben Sie m − 1 Platten von der Quelle auf den Ersatzstift , indem Sie das gleiche allgemeine Lösungsverfahren anwenden . Regeln werden nicht verletzt, nach Annahme. Dadurch verbleibt die Platte m als oberste Platte auf dem Quellstift.
2. Verschieben Sie die Platte m vom Quell- zum Ziel- Peg, was nach den Annahmen garantiert eine gültige Bewegung ist – ein einfacher Schritt .
3. Bewegen Sie die m - 1 Platten , dass wir nur auf dem Ersatz platziert haben, von dem Ersatz zum Ziel peg durch die gleichen allgemeinen Lösungsverfahren , so dass sie auf der Oberseite der Scheibe angeordnet sind , m , ohne die Regeln zu verletzen.
4. Der Basisfall besteht darin, 0 Platten zu verschieben (in den Schritten 1 und 3), also nichts zu tun – was offensichtlich nicht gegen die Regeln verstößt.

Die vollständige Tower of Hanoi-Lösung besteht dann darin, n Platten vom Quell-Peg A zum Ziel-Peg C zu verschieben, wobei B als Ersatz-Peg verwendet wird.

Dieser Ansatz kann mit mathematischer Induktion streng mathematisch bewiesen werden und wird oft als Beispiel für Rekursion im Programmierunterricht verwendet.

Logische Analyse der rekursiven Lösung

Wie bei vielen mathematischen Rätseln wird die Lösungsfindung durch das Lösen eines etwas allgemeineren Problems erleichtert: wie man einen Turm aus h (Höhe) Scheiben von einem Startstift f = A (von) auf einen Zielstift t = C (nach ), B der verbleibende dritte PEG ist und unter der Annahme , t ≠ f . Beachten Sie zunächst, dass das Problem für Permutationen der Namen der Stifte symmetrisch ist ( symmetrische Gruppe S ₃ ). Wenn eine Lösung bekannt ist, die von Peg A zu Peg C wechselt , dann kann durch Umbenennen der Pegs dieselbe Lösung für jede andere Wahl von Start- und Ziel-Peg verwendet werden. Wenn nur eine Festplatte (oder gar keine) vorhanden ist, ist das Problem trivial. Wenn h = 1, dann verschieben Sie einfach die Scheibe von Peg A nach Peg C . Wenn h > 1, dann muss irgendwo in der Bewegungsfolge die größte Scheibe von Peg A zu einem anderen Peg bewegt werden , vorzugsweise nach Peg C . Die einzige Situation, die diese Bewegung erlaubt, ist, wenn alle kleineren h − 1-Scheiben auf Peg B liegen . Daher müssen zuerst alle h − 1 kleineren Scheiben von A nach B gehen . Dann verschiebe die größte Scheibe und schließlich die h − 1 kleineren Scheiben von Peg B nach Peg C . Das Vorhandensein der größten Scheibe behindert die Bewegung der h − 1 kleineren Scheiben nicht und kann vorübergehend ignoriert werden. Nun reduziert sich das Problem darauf, h − 1 Scheiben von einem Peg auf einen anderen zu verschieben, zuerst von A nach B und dann von B nach C , aber die gleiche Methode kann beide Male verwendet werden, indem die Pegs umbenannt werden. Die gleiche Strategie kann verwendet werden, um das h − 1-Problem auf h − 2, h − 3 usw. zu reduzieren , bis nur noch eine Scheibe übrig ist. Dies wird als Rekursion bezeichnet. Dieser Algorithmus kann wie folgt schematisiert werden.

Identifizieren Sie die Platten in der Reihenfolge aufsteigender Größe durch die natürlichen Zahlen von 0 bis einschließlich h . Daher ist Scheibe 0 die kleinste und Scheibe h − 1 die größte.

Das Folgende ist ein Verfahren zum Bewegen eines Turms von h- Scheiben von einem Zapfen A auf einen Zapfen C , wobei B der verbleibende dritte Zapfen ist:

1. Wenn h > 1, dann verwenden Sie dieses Verfahren zuerst, um die h − 1 kleineren Scheiben von Peg A nach Peg B zu verschieben .
2. Nun kann die größte Scheibe, dh Scheibe h von Peg A nach Peg C verschoben werden .
3. Wenn h > 1, dann verwenden Sie dieses Verfahren erneut, um die h − 1 kleineren Scheiben von Peg B nach Peg C zu verschieben .

Mittels mathematischer Induktion lässt sich leicht beweisen, dass das obige Verfahren die minimale Anzahl von möglichen Zügen erfordert und dass die erzeugte Lösung die einzige mit dieser minimalen Anzahl von Zügen ist. Unter Verwendung von Wiederholungsbeziehungen kann die genaue Anzahl von Zügen, die diese Lösung erfordert, berechnet werden durch: . Dieses Ergebnis wird erhalten, indem man feststellt, dass die Schritte 1 und 3 Züge erfordern und dass Schritt 2 einen Zug erfordert, was ergibt . ${\displaystyle 2^{h}-1}$${\displaystyle T_{h-1}}$${\displaystyle T_{h}=2T_{h-1}+1}$

Rekursive Implementierung

Der folgende Python- Code hebt eine wesentliche Funktion der rekursiven Lösung hervor, die ansonsten missverstanden oder übersehen werden könnte. Das heißt, bei jeder Rekursionsebene invertiert der erste rekursive Aufruf die Ziel- und Hilfsstapel , während beim zweiten rekursiven Aufruf der Quell- und Hilfsstapel invertiert werden.

A = [3, 2, 1]
B = []
C = []

def move(n, source, target, auxiliary):
    if n > 0:
        # Move n - 1 disks from source to auxiliary, so they are out of the way
        move(n - 1, source, auxiliary, target)

        # Move the nth disk from source to target
        target.append(source.pop())

        # Display our progress
        print(A, B, C, '##############', sep='\n')

        # Move the n - 1 disks that we left on auxiliary onto target
        move(n - 1, auxiliary, target, source)

# Initiate call from source A to target C with auxiliary B
move(3, A, C, B)

Nicht-rekursive Lösung

Die Liste der Züge für einen Turm, der von einem Zapfen auf einen anderen übertragen wird, wie sie durch den rekursiven Algorithmus erzeugt wird, hat viele Gesetzmäßigkeiten. Beim Zählen der Züge beginnend mit 1 ist die Ordnungszahl der zu bewegenden Scheibe während des Zuges m die Anzahl der Male, die m durch 2 geteilt werden kann. Daher bezieht sich jeder ungerade Zug auf die kleinste Scheibe. Es kann auch beobachtet werden, dass die kleinste Scheibe die Zapfen f , t , r , f , t , r usw. bei ungerader Höhe des Turms durchquert und die Zapfen f , r , t , f , r , t usw. durchquert . für gleichmäßige Turmhöhe. Dies liefert den folgenden Algorithmus, der von Hand einfacher auszuführen ist als der rekursive Algorithmus.

In alternativen Zügen:

• Verschieben Sie die kleinste Festplatte auf den Stift, von dem sie nicht vor kurzem gekommen ist.
• Verschieben Sie einen anderen Datenträger legal (es gibt nur eine Möglichkeit).

Beim allerersten Zug geht die kleinste Scheibe auf peg t, wenn h ungerade ist, und auf peg r, wenn h gerade ist.

Beachten Sie auch Folgendes:

• Scheiben, deren Ordinalzahlen gerade Parität haben, bewegen sich im gleichen Sinne wie die kleinste Scheibe.
• Scheiben, deren Ordinalzahlen ungerade Parität haben, bewegen sich in entgegengesetzter Richtung.
• Wenn h gerade ist, ist der verbleibende dritte Stift während aufeinanderfolgender Bewegungen t , r , f , t , r , f usw.
• Wenn h ungerade ist, ist der verbleibende dritte Stift während aufeinanderfolgender Züge r , t , f , r , t , f usw.

Mit diesem Wissen kann ein Plattensatz in der Mitte einer optimalen Lösung ohne mehr Zustandsinformationen als die Positionen der einzelnen Platten wiederhergestellt werden:

• Nennen Sie die oben beschriebenen Züge den "natürlichen" Zug einer Scheibe.
• Untersuchen Sie die kleinste oberste Scheibe, die nicht Scheibe 0 ist, und notieren Sie, was ihr einziger (legaler) Zug wäre: Wenn es keine solche Scheibe gibt, sind wir entweder beim ersten oder letzten Zug.
• Wenn diese Bewegung die "natürliche" Bewegung der Scheibe ist, dann wurde die Scheibe seit der letzten Bewegung von Scheibe 0 nicht bewegt, und diese Bewegung sollte ausgeführt werden.
• Wenn dieser Zug nicht der "natürliche" Zug der Scheibe ist, dann bewege Scheibe 0.

Binäre Lösung

Plattenpositionen können direkter aus der binären (Basis-2) Darstellung der Zugnummer bestimmt werden (der Anfangszustand ist Zug #0 mit allen Ziffern 0 und der Endzustand ist mit allen Ziffern 1) unter Verwendung der folgenden Regeln:

• Für jede Platte gibt es eine Binärziffer ( Bit ).
• Das höchstwertige (ganz links) Bit repräsentiert die größte Platte. Ein Wert von 0 gibt an, dass sich die größte Platte auf dem ersten Peg befindet, während eine 1 anzeigt, dass sie sich auf dem letzten Peg befindet (rechter Peg, wenn die Anzahl der Platten ungerade ist, andernfalls der mittlere Peg).
• Der Bitstring wird von links nach rechts gelesen, und jedes Bit kann verwendet werden, um die Position der entsprechenden Platte zu bestimmen.
• Ein Bit mit dem gleichen Wert wie das vorherige bedeutet, dass die entsprechende Platte auf der vorherigen Platte auf demselben Stift gestapelt wird.

  (Das heißt: Eine gerade Abfolge von 1er oder 0er bedeutet, dass die entsprechenden Scheiben alle auf dem gleichen Stift liegen.)

• Ein Bit mit einem anderen Wert als das vorherige bedeutet, dass sich die entsprechende Platte eine Position links oder rechts von der vorherigen befindet. Ob links oder rechts, wird durch diese Regel bestimmt:
  • Angenommen, der Anfangsstift befindet sich auf der linken Seite.
  • Nehmen Sie auch „Wrapping“ an – der rechte Zapfen zählt also als ein Zapfen „links“ vom linken Zapfen und umgekehrt.
  • Sei n die Anzahl der größeren Platten, die sich auf demselben Peg wie ihre erste größere Platte befinden, und addiere 1 hinzu, wenn sich die größte Platte auf der linken Peg befindet. Wenn n gerade ist, befindet sich die Scheibe einen Zapfen nach rechts, ist n ungerade, befindet sich die Scheibe einen Zapfen nach links (bei einer geraden Anzahl von Scheiben und sonst umgekehrt).

Zum Beispiel in einem Hanoi mit 8 Festplatten:

• Verschiebe 0 = 00000000.
  • Die größte Platte ist 0, sie befindet sich also auf dem linken (anfänglichen) Stift.
  • Alle anderen Platten sind ebenfalls 0, also werden sie darüber gestapelt. Daher befinden sich alle Festplatten auf dem ursprünglichen Peg.
• Bewegen Sie 2 ⁸ − 1 = 11111111.
  • Die größte Scheibe ist 1, also befindet sie sich auf dem mittleren (letzten) Stift.
  • Alle anderen Disketten sind ebenfalls 1, also werden sie darüber gestapelt. Damit sind alle Disketten auf dem letzten Stift und das Puzzle ist komplett.
• Verschiebe 216 ₁₀ = 11011000.
  • Die größte Scheibe ist 1, also befindet sie sich auf dem mittleren (letzten) Stift.
  • Scheibe zwei ist ebenfalls 1, also wird sie oben auf dem mittleren Stift gestapelt.
  • Datenträger drei ist 0, also auf einem anderen Stift. Da n ungerade ist ( n = 1), liegt es einen Zapfen links, dh auf dem linken Zapfen.
  • Scheibe vier ist 1, also liegt sie auf einem anderen Stift. Da n ungerade ist ( n = 1), liegt es einen Zapfen nach links, dh auf dem rechten Zapfen.
  • Scheibe fünf ist ebenfalls 1, also wird sie oben auf dem rechten Stift gestapelt.
  • Datenträger sechs ist 0, also auf einem anderen Stift. Da n gerade ist ( n = 2), befindet sich die Scheibe einen Zapfen rechts, dh auf dem linken Zapfen.
  • Die Scheiben sieben und acht sind ebenfalls 0, also werden sie oben auf dem linken Stift gestapelt.

Die Quell- und Ziel-Pegs für den m- ten Zug lassen sich auch elegant aus der binären Darstellung von m mit bitweisen Operationen ermitteln . Um die Syntax der Programmiersprache C zu verwenden , verschieben Sie m von peg (m & m - 1) % 3zu peg ((m | m - 1) + 1) % 3, wobei die Platten auf peg 0 beginnen und auf peg 1 oder 2 enden, je nachdem, ob die Anzahl der Platten gerade oder ungerade ist. Eine andere Formulierung ist von Peg (m - (m & -m)) % 3zu Peg (m + (m & -m)) % 3.

Darüber hinaus wird die zu bewegende Platte dadurch bestimmt, wie oft der Bewegungszähler ( m ) durch 2 geteilt werden kann (dh die Anzahl der Null-Bits rechts), wobei die erste Bewegung als 1 gezählt wird und die Platten durch die Zahlen identifiziert werden 0, 1, 2 usw. in aufsteigender Reihenfolge. Dies ermöglicht eine sehr schnelle nicht-rekursive Computerimplementierung, um die Positionen der Platten nach m Bewegungen ohne Bezugnahme auf eine vorherige Bewegung oder Verteilung von Platten zu finden.

Die Operation, die die Anzahl der aufeinanderfolgenden Nullen am Ende einer Binärzahl zählt, bietet eine einfache Lösung des Problems: Die Scheiben werden von Null aus nummeriert, und bei move m wird die Zahl der nachgestellten Nullen um den minimal möglichen Abstand zu . verschoben rechts (bei Bedarf nach links zurückkreisen).

Gray-Code-Lösung

Das binäre Zahlensystem der Gray-Codes bietet eine alternative Lösung des Rätsels. Im Gray-System werden Zahlen in einer binären Kombination von Nullen und Einsen ausgedrückt, aber anstatt ein standardmäßiges Positionszahlensystem zu sein , arbeitet Gray-Code unter der Prämisse, dass sich jeder Wert von seinem Vorgänger nur um ein (und genau ein) geändertes Bit unterscheidet .

Zählt man im Gray-Code einer Bitgröße, die der Anzahl der Platten in einem bestimmten Turm von Hanoi entspricht, beginnt bei Null und zählt aufwärts, dann entspricht das bei jeder Bewegung geänderte Bit der zu bewegenden Platte, wobei das am wenigsten signifikante Bit ist die kleinste Platte, und das bedeutendste Bit ist das größte.

Zählt man die Bewegungen von 1 an und identifiziert die Scheiben durch Zahlen, die bei 0 beginnen, in aufsteigender Reihenfolge, so ist die Ordinalzahl der Scheibe, die während der Bewegung m bewegt werden soll, die Anzahl von Malen, die m durch 2 geteilt werden kann.

Diese Technik identifiziert, welche Festplatte verschoben werden soll, aber nicht wohin sie verschoben werden soll. Für die kleinste Platte gibt es immer zwei Möglichkeiten. Für die anderen Platten gibt es immer eine Möglichkeit, außer wenn alle Platten auf dem gleichen Stift liegen, aber dann muss entweder die kleinste Platte verschoben werden oder das Ziel ist bereits erreicht. Glücklicherweise gibt es eine Regel, die sagt, wohin die kleinste Festplatte verschoben werden soll. Sei f der Start-Peg, t der Ziel-Peg und r der verbleibende dritte Peg. Bei ungerader Scheibenanzahl kreist die kleinste Scheibe entlang der Zapfen in der Reihenfolge f → t → r → f → t → r usw. Bei gerader Scheibenanzahl muss dies umgekehrt werden: f → r → t → f → r → t usw.

Die Position der Bitänderung in der Gray-Code-Lösung gibt die Größe der bei jedem Schritt bewegten Scheibe an: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, ... (Sequenz A001511 im OEIS ), eine Sequenz , auch bekannt als die Lineal - Funktion oder eine mehr als die Potenz von 2 in dem Zugnummer. In der Wolfram Sprache , IntegerExponent[Range[2^8 - 1], 2] + 1gibt bewegt sich für das 8-Disk - Puzzle.

Grafische Darstellung

Das Spiel kann durch einen ungerichteten Graphen dargestellt werden , wobei die Knoten Verteilungen von Scheiben und die Kanten Züge darstellen. Für eine Festplatte ist der Graph ein Dreieck:

Der Graph für zwei Scheiben besteht aus drei Dreiecken, die verbunden sind, um die Ecken eines größeren Dreiecks zu bilden.

Ein zweiter Buchstabe wird hinzugefügt, um die größere Festplatte darzustellen. Natürlich kann es zunächst nicht verschoben werden.

Das oberste kleine Dreieck stellt nun die One-Move-Möglichkeiten mit zwei Scheiben dar:

Die Knoten an den Ecken des äußersten Dreiecks stellen Verteilungen dar, bei denen alle Scheiben auf demselben Zapfen liegen.

Nimm für h + 1-Scheiben den Graphen von h-Scheiben und ersetze jedes kleine Dreieck durch den Graphen für zwei Scheiben.

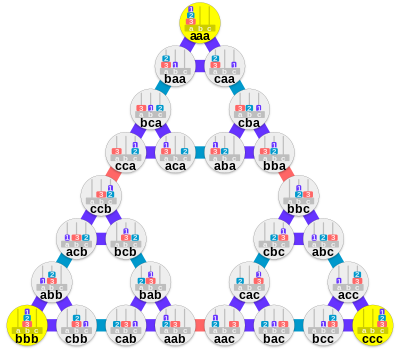
Für drei Festplatten ist das Diagramm:

Der Spielgraph von Level 7 zeigt die Verwandtschaft zum Sierpiński-Dreieck .

• nenne die Stifte a, b und c
• Listen Sie die Festplattenpositionen von links nach rechts in aufsteigender Größe auf

Die Seiten des äußersten Dreiecks stellen die kürzesten Wege dar, um einen Turm von einem Pflock zum anderen zu bewegen. Die Kante in der Mitte der Seiten des größten Dreiecks repräsentiert eine Bewegung der größten Scheibe. Die Kante in der Mitte der Seiten jedes nächstkleineren Dreiecks repräsentiert eine Bewegung der jeweils nächstkleineren Scheibe. Die Seiten der kleinsten Dreiecke repräsentieren die Bewegungen der kleinsten Scheibe.

Im Allgemeinen gibt es für ein Puzzle mit n Scheiben 3 ⁿ Knoten im Graphen; Jeder Knoten hat drei Kanten zu anderen Knoten, mit Ausnahme der drei Eckknoten, die zwei haben: Es ist immer möglich, die kleinste Scheibe auf einen der beiden anderen Stifte zu verschieben, und es ist möglich, eine Scheibe zwischen diesen beiden Stiften zu verschieben, außer in die Situation, in der alle Festplatten auf einem Stift gestapelt sind. Die Eckknoten stellen die drei Fälle dar, in denen alle Scheiben auf einem Stift gestapelt sind. Das Diagramm für n  + 1 Scheiben erhält man, indem man drei Kopien des n -Scheiben-Diagramms nimmt – jedes repräsentiert alle Zustände und Bewegungen der kleineren Scheiben für eine bestimmte Position der neuen größten Scheibe – und sie an den Ecken mit drei . verbindet neue Kanten, die die einzigen drei Möglichkeiten darstellen, die größte Platte zu bewegen. Die resultierende Figur hat somit 3 ^{n +1} Knoten und hat immer noch drei Ecken mit nur zwei Kanten.

Wenn mehr Scheiben hinzugefügt werden, ähnelt die grafische Darstellung des Spiels einer fraktalen Figur, dem Sierpiński-Dreieck . Es ist klar, dass die allermeisten Positionen im Puzzle mit der kürzestmöglichen Lösung nie erreicht werden; tatsächlich, wenn die Priester der Legende die längstmögliche Lösung verwenden (ohne eine Position erneut aufzusuchen), werden sie 3 ⁶⁴  − 1 Züge oder mehr als 10 ²³ Jahre brauchen.

Der längste sich nicht wiederholende Weg für drei Platten kann durch Löschen der nicht verwendeten Kanten visualisiert werden:

Übrigens kann dieser längste sich nicht wiederholende Weg erhalten werden, indem alle Bewegungen von a nach c verboten werden .

Der Hamilton-Zyklus für drei Scheiben lautet:

Die Grafiken zeigen deutlich, dass:

• Von jeder beliebigen Plattenverteilung gibt es genau einen kürzesten Weg, um alle Platten auf einen der drei Stifte zu verschieben.
• Zwischen jedem Paar willkürlicher Plattenverteilungen gibt es einen oder zwei verschiedene kürzeste Pfade.
• Von jeder willkürlichen Verteilung von Platten gibt es einen oder zwei verschiedene längste nicht selbstkreuzende Pfade, um alle Platten zu einem der drei Stifte zu bewegen.
• Zwischen jedem Paar willkürlicher Plattenverteilungen gibt es ein oder zwei verschiedene längste sich nicht selbst kreuzende Pfade.
• Sei N _h die Anzahl der sich nicht selbst kreuzenden Pfade zum Bewegen eines Turms von h- Scheiben von einem Zapfen zu einem anderen. Dann:
  • N ₁ = 2
  • N _{h + 1} = ( N _h ) ² + ( N _h ) ³

Daraus ergibt sich N _h zu 2, 12, 1872, 6563711232, ... (Sequenz A125295 im OEIS )

Variationen

Angrenzende Heringe

Wenn alle Bewegungen zwischen benachbarten Spielsteinen erfolgen müssen (dh bei Spielsteinen A, B, C kann man sich nicht direkt zwischen Spielsteinen A und C bewegen), dann braucht ein Stapel von n Scheiben von Spielstein A nach Spielstein C 3 ⁿ − 1 Züge. Die Lösung verwendet alle 3 ⁿ gültigen Positionen, wobei immer der eindeutige Zug ausgeführt wird, der den vorherigen Zug nicht rückgängig macht. Die Position mit allen Scheiben an Zapfen B ist zur Hälfte erreicht, dh nach (3 ⁿ − 1) / 2 Zügen.

Zyklisches Hanoi

In Cyclic Hanoi erhalten wir drei Stifte (A, B, C), die als Kreis angeordnet sind, wobei die Richtungen im Uhrzeigersinn und gegen den Uhrzeigersinn als A – B – C – A bzw. A – C – B – A definiert sind. Die Bewegungsrichtung der Scheibe muss im Uhrzeigersinn sein. Es genügt, die Reihenfolge der zu bewegenden Platten darzustellen. Die Lösung kann mit zwei sich gegenseitig rekursiven Verfahren gefunden werden:

Um n Scheiben gegen den Uhrzeigersinn zum benachbarten Zielstift zu bewegen :

1. bewege n − 1 Scheiben gegen den Uhrzeigersinn zum Zielstift
2. bewege Scheibe # n einen Schritt im Uhrzeigersinn
3. bewege n − 1 Scheiben im Uhrzeigersinn zum Startstift
4. bewege Scheibe # n einen Schritt im Uhrzeigersinn
5. bewege n − 1 Scheiben gegen den Uhrzeigersinn zum Zielstift

Um n Scheiben im Uhrzeigersinn zum benachbarten Zielstift zu bewegen :

1. verschiebe n − 1 Scheiben gegen den Uhrzeigersinn auf einen Ersatzstift
2. bewege Scheibe # n einen Schritt im Uhrzeigersinn
3. bewege n − 1 Scheiben gegen den Uhrzeigersinn zum Zielstift

Seien C(n) und A(n) die Bewegung von n Scheiben im Uhrzeigersinn und gegen den Uhrzeigersinn, dann können wir beide Formeln aufschreiben:

      C(n) = A(n-1) n A(n-1)    and      A(n) = A(n-1) n C(n-1) n A(n-1).

Thus  C(1) = 1                  and      A(1) = 1 1,
      C(2) = 1 1 2 1 1          and      A(2) = 1 1 2 1 2 1 1.

Die Lösung für das zyklische Hanoi hat einige interessante Eigenschaften:

1) Die Bewegungsmuster beim Übertragen eines Turms von Scheiben von einem Stift zu einem anderen Stift sind in Bezug auf die Mittelpunkte symmetrisch.

2) Die kleinste Scheibe ist die erste und letzte Scheibe, die bewegt wird.

3) Gruppen der kleinsten Plattenbewegungen wechseln sich mit Einzelbewegungen anderer Platten ab.

4) Die Anzahl der durch C(n) und A(n) spezifizierten Plattenbewegungen ist minimal.

Mit vier Heringe und mehr

Obwohl die Version mit drei Stiften eine einfache rekursive Lösung seit langem hat, wurde die optimale Lösung für das Problem des Turms von Hanoi mit vier Stiften (genannt Reves Puzzle) erst 2014 von Bousch verifiziert.

Bei vier oder mehr Pegs ist der Frame-Stewart-Algorithmus jedoch seit 1941 ohne Optimalitätsnachweis bekannt.

Für die formale Ableitung der genauen Anzahl von minimalen Zügen, die erforderlich sind, um das Problem durch Anwendung des Frame-Stewart-Algorithmus (und anderer äquivalenter Methoden) zu lösen, siehe das folgende Papier.

Für andere Varianten des Problems des Turms von Hanoi mit vier Zapfen siehe das Übersichtspapier von Paul Stockmeyer.

Die sogenannten Towers of Bukarest und Towers of Klagenfurt Spielkonfigurationen ergeben ternäre und pentary Gray-Codes.

Frame–Stewart-Algorithmus

Der Frame-Stewart-Algorithmus wird im Folgenden beschrieben:

• Sei die Anzahl der Festplatten.${\displaystyle n}$
• Sei die Anzahl der Stifte.${\displaystyle r}$
• Definieren Sie dies als die minimale Anzahl von Bewegungen, die erforderlich ist, um n Platten mit r Stiften zu übertragen.${\displaystyle T(n,r)}$

Der Algorithmus lässt sich rekursiv beschreiben:

1. Bei einigen , übertragen Sie die obersten Scheiben auf einen anderen Stift als den Start- oder Zielstift und führen Sie Bewegungen aus.${\displaystyle k}$${\displaystyle 1\leq k<n}$${\displaystyle k}$${\displaystyle T(k,r)}$
2. Ohne den Stift zu stören, der jetzt die obersten Scheiben enthält , übertragen Sie die verbleibenden Scheiben auf den Zielstift, indem Sie nur die verbleibenden Stifte verwenden und Bewegungen ausführen.${\displaystyle k}$${\displaystyle nk}$${\displaystyle r-1}$${\displaystyle T(nk,r-1)}$
3. Schließlich übertragen Sie die oberen Scheiben auf den Zielstift und machen Sie Bewegungen.${\displaystyle k}$${\displaystyle T(k,r)}$

Der gesamte Prozess erfordert Bewegungen. Daher sollte die Anzahl kommissioniert werden, für die diese Menge minimal ist. Im 4-Stift-Fall ist das Optimum gleich , wobei die nächste ganzzahlige Funktion ist . Im UPenn CIS 194-Kurs zu Haskell beispielsweise listet die erste Aufgabenseite die optimale Lösung für den Fall von 15 Platten und 4 Stiften als 129 Schritte auf, die für den obigen Wert von k erhalten wird . ${\displaystyle 2T(k,r)+T(nk,r-1)}$${\displaystyle k}$${\displaystyle k}$${\displaystyle n-\left\lfloor {\sqrt {2n+1}}\right\rceil +1}$${\displaystyle \left\lfloor \cdot \right\rceil}$

Es wird angenommen, dass dieser Algorithmus für eine beliebige Anzahl von Stiften optimal ist; seine Zugzahl beträgt 2 ^{Θ ( n 1/( r −2) )} (für festes r ).

Allgemeine kürzeste Wege und die Nummer 466/885

Eine kuriose Verallgemeinerung des ursprünglichen Ziels des Puzzles besteht darin, von einer gegebenen Konfiguration der Scheiben auszugehen, bei der sich nicht unbedingt alle Scheiben auf demselben Stift befinden, und in einer minimalen Anzahl von Zügen zu einer anderen gegebenen Konfiguration zu gelangen. Im Allgemeinen kann es ziemlich schwierig sein, eine kürzeste Zugfolge zu berechnen, um dieses Problem zu lösen. Eine Lösung wurde von Andreas Hinz vorgeschlagen und basiert auf der Beobachtung, dass in einer kürzesten Folge von Zügen die größte Scheibe, die bewegt werden muss (natürlich kann man alle größten Scheiben ignorieren, die sowohl im Anfangs- als auch im Endkonfigurationen) werden entweder genau einmal oder genau zweimal verschoben.

Die mit diesem verallgemeinerten Problem verbundene Mathematik wird noch interessanter, wenn man die durchschnittliche Anzahl von Zügen in einer kürzesten Zugfolge zwischen zwei zufällig ausgewählten anfänglichen und endgültigen Scheibenkonfigurationen betrachtet. Hinz und Chan Tat-Hung haben unabhängig voneinander festgestellt (siehe auch ), dass die durchschnittliche Anzahl der Züge in einem n-Scheiben-Turm durch die folgende genaue Formel gegeben ist:

${\displaystyle {\frac {466}{885}}\cdot 2^{n}-{\frac {1}{3}}-{\frac {3}{5}}\cdot \left({\frac {1}{3}}\right)^{n}+\left({\frac {12}{59}}+{\frac {18}{1003}}{\sqrt {17}}\right)\ left({\frac {5+{\sqrt {17}}}{18}}\right)^{n}+\left({\frac {12}{59}}-{\frac {18}{1003 }}{\sqrt {17}}\right)\left({\frac {5-{\sqrt {17}}}{18}}\right)^{n}.}$

Wenn n groß genug ist , konvergieren nur der erste und der zweite Term nicht gegen Null, so dass wir einen asymptotischen Ausdruck erhalten : , as . Intuitiv könnten wir also den Bruchteil von als das Verhältnis der Arbeit interpretieren, die man leisten muss, wenn man von einer zufällig gewählten Konfiguration zu einer anderen zufällig gewählten Konfiguration wechselt, relativ zu der Schwierigkeit, den "schwierigsten" Weg der Länge zu überwinden, der beinhaltet das Verschieben aller Festplatten von einem Stift zum anderen. Eine alternative Erklärung für das Auftreten der Konstanten 466/885 sowie ein neuer und etwas verbesserter Algorithmus zur Berechnung des kürzesten Weges lieferte Romik. ${\displaystyle 466/885\cdot 2^{n}-1/3+o(1)}$${\displaystyle n\to\infty}$${\displaystyle 466/885\ca. 52,6\%}$${\displaystyle 2^{n}-1}$

Magnetisches Hanoi

In Magnetic Tower of Hanoi hat jede Scheibe zwei unterschiedliche Seiten Nord und Süd (normalerweise "rot" und "blau"). Scheiben dürfen nicht mit den gleichen Polen zusammen platziert werden – Magnete in jeder Scheibe verhindern diese illegale Bewegung. Außerdem muss jede Scheibe beim Bewegen umgedreht werden.

Erstkonfiguration der zweifarbigen Türme von Hanoi (n=4)

Zweifarbige Türme von Hanoi

Diese Variante des berühmten Puzzles Turm von Hanoi wurde im Juli 1988 den Schülern der 3. bis 6. Klasse des 2ème Championnat de France des Jeux Mathématiques et Logiques angeboten .

Endgültige Konfiguration der zweifarbigen Türme von Hanoi (n=4)

Die Regeln des Puzzles sind im Wesentlichen die gleichen: Scheiben werden einzeln zwischen den Stiften verschoben. Zu keinem Zeitpunkt darf eine größere Scheibe auf eine kleinere gelegt werden. Der Unterschied besteht darin, dass es jetzt für jede Größe zwei Scheiben gibt: eine schwarze und eine weiße. Außerdem gibt es jetzt zwei Türme aus Scheiben in wechselnden Farben. Das Ziel des Puzzles ist es, die Türme einfarbig (gleiche Farbe) zu machen. Es wird angenommen, dass die größten Scheiben am unteren Ende der Türme die Positionen tauschen.

Turm von Hanoy

Eine Variation des Puzzles wurde als Solitärspiel mit neun Spielkarten unter dem Namen Tower of Hanoy adaptiert . Es ist nicht bekannt, ob die geänderte Schreibweise des ursprünglichen Namens beabsichtigt oder zufällig ist.

Anwendungen

Topografisches 3D-AFM-Bild eines mehrschichtigen Palladium-Nanoblatts auf einem Siliziumwafer mit einem Turm mit Hanoi-ähnlicher Struktur.

Der Turm von Hanoi wird häufig in der psychologischen Problemlösungsforschung verwendet . Es gibt auch eine Variante dieser Aufgabe namens Tower of London zur neuropsychologischen Diagnostik und Behandlung von Exekutivfunktionen.

Zhang und Norman verwendeten mehrere isomorphe (äquivalente) Darstellungen des Spiels, um den Einfluss des Darstellungseffekts auf das Aufgabendesign zu untersuchen. Sie zeigten einen Einfluss auf die Benutzerleistung, indem sie die Art und Weise änderten, wie die Spielregeln dargestellt werden, indem Variationen im physischen Design der Spielkomponenten verwendet wurden. Dieses Wissen ist in die Entwicklung des TURF-Frameworks zur Darstellung der Mensch-Computer-Interaktion eingeflossen .

Der Turm von Hanoi wird auch als verwendet Backup - Rotationsschema , wenn Computerdaten , um Sicherungen in denen mehrere Bänder / Medien beteiligt sind.

Wie bereits erwähnt, ist der Turm von Hanoi beliebt, um Anfängern in der Programmierung rekursive Algorithmen beizubringen. Eine bildhafte Version dieses Puzzles ist in den Emacs- Editor programmiert, auf den Sie durch Eingabe von Mx Hanoi zugreifen können. Es gibt auch einen Beispielalgorithmus, der in Prolog geschrieben ist .

Der Turm von Hanoi wird auch als Test von Neuropsychologen verwendet, die versuchen, Frontallappendefizite zu bewerten .

Im Jahr 2010 veröffentlichten Forscher die Ergebnisse eines Experiments, bei dem festgestellt wurde, dass die Ameisenart Linepithema humile die 3-Scheiben-Version des Turms von Hanoi-Problem durch nichtlineare Dynamik und Pheromonsignale erfolgreich lösen konnte.

Im Jahr 2014 synthetisierten Wissenschaftler mehrschichtige Palladium-Nanoblätter mit einer dem Turm von Hanoi ähnlichen Struktur.

In der Populärkultur

In der Science-Fiction-Geschichte "Now Inhale" von Eric Frank Russell wird ein Mensch auf einem Planeten gefangen gehalten, auf dem der lokale Brauch darin besteht, den Gefangenen ein Spiel spielen zu lassen, bis es vor seiner Hinrichtung gewonnen oder verloren ist. Der Protagonist weiß, dass es ein Jahr oder länger dauern kann, bis ein Rettungsschiff eintrifft, also entscheidet er sich dafür, Towers of Hanoi mit 64 Disketten zu spielen. Diese Geschichte nimmt Bezug auf die Legende über die buddhistischen Mönche, die das Spiel bis zum Ende der Welt spielen.

In der Doctor Who- Geschichte The Celestial Toymaker aus dem Jahr 1966 zwingt der gleichnamige Bösewicht den Doctor , ein zehnteiliges, 1.023 Züge umfassendes Tower of Hanoi-Spiel mit dem Titel The Trilogic Game zu spielen, bei dem die Teile beim Stapeln eine Pyramidenform bilden.

Im Jahr 2007 wurde das Konzept des Towers Of Hanoi-Problems in Professor Layton und der Diabolical Box in den Rätseln 6, 83 und 84 verwendet, aber die Scheiben wurden zu Pfannkuchen geändert. Das Puzzle basierte auf einem Dilemma, bei dem der Koch eines Restaurants einen Stapel Pfannkuchen von einem Teller auf den anderen bewegen musste, mit den Grundprinzipien des ursprünglichen Puzzles (dh drei Teller, auf die die Pfannkuchen verschoben werden konnten, ohne in der Lage zu sein, einen größeren Pfannkuchen auf einen kleineren legen usw.)

Im Film Rise of the Planet of the Apes (2011) wird dieses Puzzle, das im Film "Lucas Tower" genannt wird, als Test verwendet, um die Intelligenz von Affen zu untersuchen.

Das Puzzle wird regelmäßig in Abenteuer- und Puzzlespielen vorgestellt . Da es einfach zu implementieren und leicht zu erkennen ist, eignet es sich gut als Puzzle in einem größeren Grafikspiel (zB Star Wars: Knights of the Old Republic und Mass Effect ). Einige Implementierungen verwenden gerade Scheiben, andere verbergen das Rätsel jedoch in einer anderen Form. Es gibt eine Arcade-Version von Sega .

Eine 15-Disk-Version des Puzzles erscheint im Spiel Sunless Sea als Schloss zu einem Grab. Der Spieler hat die Möglichkeit, sich durch jeden Zug des Puzzles zu klicken, um es zu lösen, aber das Spiel merkt an, dass es 32767 Züge braucht, um es abzuschließen. Wenn ein besonders engagierter Spieler sich bis zum Ende des Puzzles durchklickt, stellt sich heraus, dass das Beenden des Puzzles die Tür nicht aufschließt.

In Yu-Gi-Oh! VRAINS , eine Hacker-Gruppe namens "Knight of Hanoi", erstellt eine Struktur namens "Tower of Hanoi" innerhalb des gleichnamigen Virtual-Reality-Netzwerks VRAINS.

Dies wurde erstmals 2002 in Survivor Thailand als Herausforderung eingesetzt, aber anstelle von Ringen wurden die Stücke einem Tempel ähneln. Sook Jai stellte sich der Herausforderung, Jed loszuwerden, obwohl Shii-Ann genau wusste, wie man das Rätsel löst. Das Problem wird als Teil einer Belohnungsherausforderung in einer Folge der amerikanischen Version der TV-Serie Survivor aus dem Jahr 2011 vorgestellt . Beide Spieler ( Ozzy Lusth und Benjamin "Coach" Wade ) hatten Mühe, das Rätsel zu lösen, und wurden dabei von ihren Stammeskollegen unterstützt.

Siehe auch

Teil einer Serie über
Rätsel
Typen Raten Rätsel Situation Logik Präparation Induktion Logikraster Selbstreferenz Mechanisch Kombination Konstruktion Entwirrung Sperren Gehe Probleme Falten Stock Fliesen Tour Gleiten Schach Labyrinth  ( Logisches Labyrinth ) Wort und Zahl Kreuzworträtsel Sudoku Puzzle-Videospiele Labyrinthe Metapuzzles
Themen Rätsel Dilemma Optische Täuschung Verpackungsprobleme Paradox Probleme lösen Puzzlejagd Syllogismus in andere Richtungen denken
Listen Unmögliche Rätsel Labyrinth-Videospiele Nikoli-Rätseltypen Puzzle-Videospiele Rätselthemen
v T e

• ABACABA-Muster
• Backup-Rotationsschema , eine TOH-Anwendung
• Baguenaudier
• Rekursion (Informatik)

Anmerkungen

Externe Links

• Weisstein, Eric W. "Turm von Hanoi" . MathWorld .