Heronisches Dreieck - Heronian triangle
In Geometrie , ein Heronisches Dreieck ist ein Dreieck , das Seitenlängen aufweist und Bereich , die alle sind ganze Zahlen . Heronische Dreiecke sind nach dem Helden von Alexandria benannt . Der Begriff wird manchmal breiter auf Dreiecke angewendet, deren Seiten und Fläche alle rationale Zahlen sind , da man die Seiten um ein gemeinsames Vielfaches neu skalieren kann, um ein Dreieck zu erhalten, das im obigen Sinne heronisch ist.
Eigenschaften
Jedes rechtwinklige Dreieck, dessen Seitenlängen ein pythagoräisches Tripel sind, ist ein Heronisches Dreieck, da die Seitenlängen eines solchen Dreiecks ganze Zahlen sind und seine Fläche ebenfalls eine ganze Zahl ist, da sie die Hälfte des Produkts der beiden kürzeren Seiten des Dreiecks ist, at mindestens einer davon muss gerade sein.
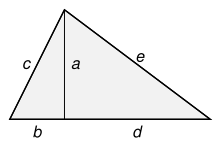
Ein Beispiel für ein nicht rechtwinkliges Heronisches Dreieck ist das gleichschenklige Dreieck mit den Seitenlängen 5, 5 und 6, dessen Fläche 12 ist. Dieses Dreieck erhält man, indem man zwei Kopien des rechtwinkligen Dreiecks mit den Seiten 3, 4, und 5 entlang der Seiten der Länge 4. Dieser Ansatz funktioniert im Allgemeinen, wie im nebenstehenden Bild dargestellt. Man nimmt ein pythagoräisches Tripel ( a , b , c ), wobei c am größten ist, dann ein anderes ( a , d , e ), wobei e am größten ist, konstruiert die Dreiecke mit diesen Seitenlängen und verbindet sie entlang der Seitenlängen a , um ein Dreieck mit ganzzahligen Seitenlängen c , e und b + d zu erhalten , und mit Fläche
- (die Hälfte mal die Basis mal die Höhe).
Wenn a gerade ist, ist die Fläche A eine ganze Zahl. Weniger offensichtlich, wenn a ungerade ist, ist A immer noch eine ganze Zahl, da b und d beide gerade sein müssen, was b + d auch gerade macht.
Einige heronische Dreiecke können nicht durch Zusammenfügen zweier rechtwinkliger Dreiecke mit ganzzahligen Seiten wie oben beschrieben erhalten werden. Zum Beispiel kann ein 5, 29, 30 Heronisches Dreieck mit Fläche 72 nicht aus zwei ganzzahligen pythagoräischen Dreiecken konstruiert werden, da keine seiner Höhen ganze Zahlen sind. Auch kann kein primitives pythagoräisches Dreieck aus zwei kleineren ganzzahligen pythagoräischen Dreiecken konstruiert werden. Solche heronischen Dreiecke werden als unzerlegbar bezeichnet . Wenn man jedoch pythagoreische Tripel mit rationalen Werten, nicht unbedingt ganzen Zahlen, zulässt, dann existiert immer eine Zerlegung in rechtwinklige Dreiecke mit rationalen Seiten, denn jede Höhe eines heronischen Dreiecks ist rational (da sie gleich dem doppelten ganzzahligen Bereich geteilt durch die ganzzahlige Basis ist) . Das heronische Dreieck mit den Seiten 5, 29, 30 kann also aus rationalen pythagoräischen Dreiecken mit den Seiten 7/5, 24/5, 5 und 143/5, 24/5, 29 konstruiert werden. Beachten Sie, dass ein pythagoräisches Tripel mit rationalen Werten gerade . ist eine skalierte Version eines Tripels mit ganzzahligen Werten.
Andere Eigenschaften von Heronschen Dreiecken sind wie folgt:
- Der Umfang eines Heronschen Dreiecks ist immer eine gerade Zahl. Somit hat jedes Heronische Dreieck eine ungerade Anzahl von Seiten gerader Länge, und jedes primitive Heronische Dreieck hat genau eine gerade Seite.
- Der Semiperimeter s eines Heronschen Dreiecks mit den Seiten a , b und c kann niemals prim sein. Dies kann daran gesehen werden, dass s(s−a)(s−b)(s−c) ein perfektes Quadrat sein muss und wenn s eine Primzahl ist, dann muss einer der anderen Terme s als Faktor haben, aber dies ist unmöglich, da diese Begriffe alle kleiner als s sind .
- Die Fläche eines Heronschen Dreiecks ist immer durch 6 teilbar.
- Alle Höhen eines heronischen Dreiecks sind rational. Dies kann daran gesehen werden, dass die Fläche eines Dreiecks die Hälfte einer Seite mal seiner Höhe von dieser Seite beträgt und ein heronisches Dreieck ganzzahlige Seiten und Flächen hat. Einige heronische Dreiecke haben drei nicht ganzzahlige Höhen, zum Beispiel das spitze (15, 34, 35) mit der Fläche 252 und das stumpfe (5, 29, 30) mit der Fläche 72. Jedes heronische Dreieck mit einer oder mehreren nicht ganzzahligen Höhen kann um einen Faktor hochskaliert werden, der dem kleinsten gemeinsamen Vielfachen der Höhennenner entspricht , um ein ähnliches Heronisches Dreieck mit drei ganzzahligen Höhen zu erhalten.
- Heronische Dreiecke ohne ganzzahlige Höhe ( unzerlegbar und nicht-pythagoräisch) haben Seiten, die alle durch Primzahlen der Form 4 k +1 teilbar sind . Zerlegbare heronische Dreiecke müssen jedoch zwei Seiten haben, die die Hypotenuse von pythagoräischen Dreiecken sind. Daher haben alle heronischen Dreiecke, die nicht Pythagoras sind, mindestens zwei Seiten, die durch Primzahlen der Form 4 k +1 teilbar sind . Übrig bleiben pythagoräische Dreiecke. Daher haben alle Heronschen Dreiecke mindestens eine Seite, die durch Primzahlen der Form 4 k +1 teilbar ist . Wenn ein Heronisches Dreieck schließlich nur eine Seite hat, die durch Primzahlen der Form 4 k +1 teilbar ist, muss es pythagoräisch sein mit der Seite als Hypotenuse und die Hypotenuse muss durch 5 teilbar sein .
- Alle die Innen senkrechten Halbierenden eines Heronisches Dreieck rational sind: Für jedes Dreieck diese sind gegeben durch und wo die Seiten a ≥ b ≥ c und die Fläche ist A ; in einem Heronschen Dreieck sind alle a , b , c und A ganze Zahlen.
- Es gibt keine gleichseitigen heronischen Dreiecke.
- Es gibt keine heronischen Dreiecke mit einer Seitenlänge von 1 oder 2.
- Es gibt unendlich viele primitive Heronische Dreiecke mit einer Seitenlänge gleich a, vorausgesetzt a > 2.
- Es gibt keine heronischen Dreiecke, deren Seitenlängen einen geometrischen Verlauf bilden .
- Wenn zwei Seiten (aber nicht drei) eines Heronschen Dreiecks einen gemeinsamen Faktor haben, muss dieser Faktor die Summe zweier Quadrate sein.
- Jeder Winkel eines Heronschen Dreiecks hat einen rationalen Sinus. Dies folgt aus der Flächenformel Fläche = (1/2) ab sin C , in der die Fläche und die Seiten a und b ganze Zahlen sind, und äquivalent für die anderen Winkel.
- Jeder Winkel eines Heronschen Dreiecks hat einen rationalen Kosinus. Dies ergibt sich aus dem Gesetz des Kosinus , c 2 = ein 2 + b 2 - 2 ab cos C , in dem die Seiten a , b und c ganze Zahlen sind, und die in äquivalenter Weise für den anderen Winkel.
- Da alle Heronschen Dreiecke alle Winkel Sinus und Kosinus rational haben, bedeutet dies, dass jeder schiefe Winkel eines Heronschen Dreiecks einen rationalen Tangens, Kotangens, Sekanten und Kosekansen hat. Außerdem hat die Hälfte jedes Winkels einen rationalen Tangens, weil tan C/2 = sin C / (1 + cos C) und äquivalent für andere Winkel.
- Es gibt keine heronischen Dreiecke, deren drei Innenwinkel eine arithmetische Folge bilden. Dies liegt daran, dass alle ebenen Dreiecke mit Winkeln in einer arithmetischen Folge einen Winkel von 60° haben müssen, der keinen rationalen Sinus hat.
- Jedes Quadrat, das in ein Heronisches Dreieck eingeschrieben ist, hat rationale Seiten: Für ein allgemeines Dreieck hat das eingeschriebene Quadrat auf der Seite der Länge a eine Länge, wobei A die Fläche des Dreiecks ist; in einem Heronschen Dreieck sind sowohl A als auch a ganze Zahlen.
- Jedes heronische Dreieck hat einen rationalen Innenradius (Radius seines eingeschriebenen Kreises): Bei einem allgemeinen Dreieck ist der Innenradius das Verhältnis der Fläche zum halben Umfang, und beide sind in einem Heronischen Dreieck rational.
- Jedes heronische Dreieck hat einen rationalen Umkreisradius (den Radius seines umschriebenen Kreises): Für ein allgemeines Dreieck ist der Umkreisradius gleich einem Viertel des Produkts der Seiten geteilt durch die Fläche; in einem Heronschen Dreieck sind die Seiten und die Fläche ganze Zahlen.
- In einem Heronschen Dreieck ist der Abstand vom Schwerpunkt zu jeder Seite rational, da dieser Abstand bei allen Dreiecken das Verhältnis der doppelten Fläche zu der dreifachen Seitenlänge ist. Dies kann verallgemeinert werden, indem man feststellt, dass alle Zentren, die mit Heronschen Dreiecken verbunden sind, deren baryzentrische Koordinaten rationale Verhältnisse sind, einen rationalen Abstand zu jeder Seite haben. Diese Zentren gehören die circumcenter , Höhenschnittpunkt , Neun-Punkte - Zentrum , Symmediane Punkt , Gergonne Punkt und Nagel Punkt .
- Alle heronischen Dreiecke können auf einem Gitter platziert werden, wobei jeder Scheitelpunkt an einem Gitterpunkt liegt.
Genaue Formel für alle Heronischen Dreiecke
Der indische Mathematiker Brahmagupta (598-668 n. Chr.) leitete die parametrische Lösung so ab, dass jedes heronische Dreieck Seiten proportional zu:
für ganze Zahlen m , n und k wobei:
- .
Der Proportionalitätsfaktor ist in der Regel ein rationaler p / q , wo q = gcd ( a, b, c ) , um den erzeugten Heronisches Dreieck zu seinen ursprünglichen und reduziert p Skalen bis diesem primitiven auf die gewünschte Größe. Nimmt man beispielsweise m = 36, n = 4 und k = 3, so ergibt sich ein Dreieck mit a = 5220, b = 900 und c = 5400, das dem 5, 29, 30 Heronschen Dreieck ähnlich ist und der verwendete Proportionalitätsfaktor hat p = 1 und q = 180.
Das Hindernis für eine rechnerische Verwendung der parametrischen Lösung von Brahmagupta ist der Nenner q des Proportionalitätsfaktors. q kann nur durch Berechnung des größten gemeinsamen Teilers der drei Seiten ( gcd( a, b, c ) ) bestimmt werden und bringt ein Element der Unvorhersehbarkeit in den Erzeugungsprozess ein. Der einfachste Weg, Listen von Heronschen Dreiecken zu generieren, besteht darin, alle ganzzahligen Dreiecke bis zu einer maximalen Seitenlänge zu generieren und auf eine ganzzahlige Fläche zu testen.
Schnellere Algorithmen wurden von Kurz (2008) abgeleitet .
Es gibt unendlich viele primitive und unzerlegbare nicht-pythagoräische heronische Dreiecke mit ganzzahligen Werten für den Innenradius und alle drei Exradien , einschließlich der von . erzeugten
Es gibt unendlich viele Heronische Dreiecke, die auf einem Gitter platziert werden können, so dass nicht nur die Scheitelpunkte an Gitterpunkten liegen, wie es für alle Heronschen Dreiecke gilt, sondern zusätzlich die Mittelpunkte der In- und Exkreise an Gitterpunkten liegen.
Siehe auch Formeln für Heronische Dreiecke mit einem Winkel gleich zweimal dem anderen , Heronische Dreiecke mit Seiten in arithmetischer Folge und gleichschenklige Heronische Dreiecke .
Alle heronischen Dreiecke aus Halbwinkeltangenten
Der Tangens der Hälfte eines beliebigen Innenwinkels eines heronischen Dreiecks ist notwendigerweise rational; siehe Eigenschaften oben. Diese Halbwinkel sind positiv und summieren sich zu 90° ( π /2 Radiant), weil die Innenwinkel ( A , B , C ) jedes Dreiecks sich zu 180° ( π Radiant) summieren . Wir beginnen damit, dass wir r = tan( A /2) und s = tan( B /2) als beliebige positive rationale Zahlen wählen, die rs < 1 erfüllen . Die Grenze von 1 stellt sicher, dass der Winkel A /2 + B /2 kleiner als 90° ist und somit der Winkel C /2 positiv ist. Der Wert t = tan( C /2) wird auch eine positive rationale Zahl sein, weil
Wir können den Sinus eines Winkels unter Verwendung der Formel berechnet werden , so dass die Sinusse aus sind jeweils. Diese Werte sind rational, weil die Werte von r , s und t rational sind.
Wir verwenden das Sinusgesetz, um zu schließen, dass die Seitenlängen des Dreiecks proportional zu diesen Sinus sind. Ganzzahlwerte für die Seitenlängen erhält man, indem man die Sinus mit dem kleinsten gemeinsamen Vielfachen ihrer Nenner multipliziert und dann durch den größten gemeinsamen Faktor der Ergebnisse dividiert. Somit haben wir die Seitenlängen eines primitiven heronischen Dreiecks aus seinen Halbwinkeltangenten berechnet.
Wenn auch r , s oder t gleich 1 ist, dann ist der entsprechende Innenwinkel ein rechter Winkel und die drei Seiten definieren ebenfalls ein pythagoräisches Tripel .
Beispiele
Die Liste der primitiven ganzzahligen Heronschen Dreiecke, sortiert nach Fläche und, wenn diese gleich ist, nach Umfang , beginnt wie in der folgenden Tabelle. „Primitiv“ bedeutet, dass der größte gemeinsame Teiler der drei Seitenlängen gleich 1 ist.
| Bereich | Umfang | Seitenlänge b+d | Seitenlänge e | Seitenlänge c |
|---|---|---|---|---|
| 6 | 12 | 5 | 4 | 3 |
| 12 | 16 | 6 | 5 | 5 |
| 12 | 18 | 8 | 5 | 5 |
| 24 | 32 | fünfzehn | 13 | 4 |
| 30 | 30 | 13 | 12 | 5 |
| 36 | 36 | 17 | 10 | 9 |
| 36 | 54 | 26 | 25 | 3 |
| 42 | 42 | 20 | fünfzehn | 7 |
| 60 | 36 | 13 | 13 | 10 |
| 60 | 40 | 17 | fünfzehn | 8 |
| 60 | 50 | 24 | 13 | 13 |
| 60 | 60 | 29 | 25 | 6 |
| 66 | 44 | 20 | 13 | 11 |
| 72 | 64 | 30 | 29 | 5 |
| 84 | 42 | fünfzehn | 14 | 13 |
| 84 | 48 | 21 | 17 | 10 |
| 84 | 56 | 25 | 24 | 7 |
| 84 | 72 | 35 | 29 | 8 |
| 90 | 54 | 25 | 17 | 12 |
| 90 | 108 | 53 | 51 | 4 |
| 114 | 76 | 37 | 20 | 19 |
| 120 | 50 | 17 | 17 | 16 |
| 120 | 64 | 30 | 17 | 17 |
| 120 | 80 | 39 | 25 | 16 |
| 126 | 54 | 21 | 20 | 13 |
| 126 | 84 | 41 | 28 | fünfzehn |
| 126 | 108 | 52 | 51 | 5 |
| 132 | 66 | 30 | 25 | 11 |
| 156 | 78 | 37 | 26 | fünfzehn |
| 156 | 104 | 51 | 40 | 13 |
| 168 | 64 | 25 | 25 | 14 |
| 168 | 84 | 39 | 35 | 10 |
| 168 | 98 | 48 | 25 | 25 |
| 180 | 80 | 37 | 30 | 13 |
| 180 | 90 | 41 | 40 | 9 |
| 198 | 132 | 65 | 55 | 12 |
| 204 | 68 | 26 | 25 | 17 |
| 210 | 70 | 29 | 21 | 20 |
| 210 | 70 | 28 | 25 | 17 |
| 210 | 84 | 39 | 28 | 17 |
| 210 | 84 | 37 | 35 | 12 |
| 210 | 140 | 68 | 65 | 7 |
| 210 | 300 | 149 | 148 | 3 |
| 216 | 162 | 80 | 73 | 9 |
| 234 | 108 | 52 | 41 | fünfzehn |
| 240 | 90 | 40 | 37 | 13 |
| 252 | 84 | 35 | 34 | fünfzehn |
| 252 | 98 | 45 | 40 | 13 |
| 252 | 144 | 70 | 65 | 9 |
| 264 | 96 | 44 | 37 | fünfzehn |
| 264 | 132 | 65 | 34 | 33 |
| 270 | 108 | 52 | 29 | 27 |
| 288 | 162 | 80 | 65 | 17 |
| 300 | 150 | 74 | 51 | 25 |
| 300 | 250 | 123 | 122 | 5 |
| 306 | 108 | 51 | 37 | 20 |
| 330 | 100 | 44 | 39 | 17 |
| 330 | 110 | 52 | 33 | 25 |
| 330 | 132 | 61 | 60 | 11 |
| 330 | 220 | 109 | 100 | 11 |
| 336 | 98 | 41 | 40 | 17 |
| 336 | 112 | 53 | 35 | 24 |
| 336 | 128 | 61 | 52 | fünfzehn |
| 336 | 392 | 195 | 193 | 4 |
| 360 | 90 | 36 | 29 | 25 |
| 360 | 100 | 41 | 41 | 18 |
| 360 | 162 | 80 | 41 | 41 |
| 390 | 156 | 75 | 68 | 13 |
| 396 | 176 | 87 | 55 | 34 |
| 396 | 198 | 97 | 90 | 11 |
| 396 | 242 | 120 | 109 | 13 |
Listen von primitiven heronischen Dreiecken, deren Seiten 6.000.000 nicht überschreiten, finden Sie unter "Listen von primitiven heronischen Dreiecken" . Sascha Kurz, Universität Bayreuth, Deutschland. Archiviert (PDF) vom Original im Mai 2016 . Abgerufen am 29. März 2016 .
Gleiche Dreiecke
Eine Form heißt gleich, wenn ihre Fläche ihrem Umfang entspricht. Es gibt genau fünf gleiche Heronische Dreiecke: die mit den Seitenlängen (5,12,13), (6,8,10), (6,25,29), (7,15,20) und (9,10 ,17).
Fast gleichseitige heronische Dreiecke
Da die Fläche eines gleichseitigen Dreiecks mit rationalen Seiten eine irrationale Zahl ist , ist kein gleichseitiges Dreieck heronisch. Es gibt jedoch eine einzigartige Folge von Heronschen Dreiecken, die "fast gleichseitig" sind, weil die drei Seiten die Form n − 1, n , n + 1 haben. Eine Methode zur Generierung aller Lösungen dieses Problems basierend auf Kettenbrüchen wurde in . beschrieben 1864 von Edward Sang und 1880 gab Reinhold Hoppe einen geschlossenen Ausdruck für die Lösungen. Die ersten Beispiele dieser fast gleichseitigen Dreiecke sind in der folgenden Tabelle aufgeführt (Sequenz A003500 im OEIS ):
| Seitenlänge | Bereich | Umkreis | ||
|---|---|---|---|---|
| n − 1 | n | n + 1 | ||
| 3 | 4 | 5 | 6 | 1 |
| 13 | 14 | fünfzehn | 84 | 4 |
| 51 | 52 | 53 | 1170 | fünfzehn |
| 193 | 194 | 195 | 16296 | 56 |
| 723 | 724 | 725 | 226974 | 209 |
| 2701 | 2702 | 2703 | 3161340 | 780 |
| 10083 | 10084 | 10085 | 44031786 | 2911 |
| 37633 | 37634 | 37635 | 613283664 | 10864 |
Nachfolgende Werte von n können gefunden werden, indem man den vorherigen Wert mit 4 multipliziert und dann den Wert davor subtrahiert (52 = 4 × 14 − 4, 194 = 4 × 52 − 14 usw.), also:
wobei t eine beliebige Zeile in der Tabelle bezeichnet. Dies ist eine Lucas-Sequenz . Alternativ generiert die Formel alle n . Äquivalent sei A = Fläche und y = Innenradius, dann gilt
wobei { n , y } Lösungen von n 2 − 12 y 2 = 4 sind. Eine kleine Transformation n = 2x liefert eine konventionelle Pell-Gleichung x 2 − 3 y 2 = 1, deren Lösungen dann aus der regulären Fortsetzung abgeleitet werden können Bruchentwicklung für √ 3 .
Die Variable n hat die Form , wobei k 7, 97, 1351, 18817, … ist. Die Zahlen in dieser Folge haben die Eigenschaft, dass k aufeinanderfolgende ganze Zahlen eine ganzzahlige Standardabweichung haben .
Siehe auch
Verweise
Externe Links
- Weisstein, Eric W. "Heronisches Dreieck" . MathWorld .
- Online-Enzyklopädie der Integer-Sequenzen Heronian
- Wm. Fitch Cheney, Jr. (Januar 1929), "Heronian Triangles", Amer. Mathematik. Monatlich , 36 (1): 22–28, doi : 10.1080/00029890.1929.11986902 , JSTOR 2300173
- S. sch. Kozhegel'dinov (1994), "Über fundamentale heronische Dreiecke", Math. Anmerkungen , 55 (2): 151–6, doi : 10.1007/BF02113294 , S2CID 115233024