Hyperebenen-Trennungssatz - Hyperplane separation theorem

In der Geometrie ist der Hyperebenen-Trennungssatz ein Satz über disjunkte konvexe Mengen im n- dimensionalen euklidischen Raum . Es gibt mehrere ziemlich ähnliche Versionen. In einer Version des Theorems, wenn diese beiden Mengen abgeschlossen sind und mindestens eine von ihnen kompakt ist , dann gibt es eine Hyperebene zwischen ihnen und sogar zwei parallele Hyperebenen dazwischen, die durch eine Lücke getrennt sind. In einer anderen Version, wenn beide disjunkten konvexen Mengen offen sind, gibt es eine Hyperebene zwischen ihnen, aber nicht unbedingt eine Lücke. Eine Achse, die orthogonal zu einer trennenden Hyperebene ist, ist eine Trennachse , weil die orthogonalen Projektionen der konvexen Körper auf die Achse disjunkt sind.

Der Hyperebenen-Trennsatz geht auf Hermann Minkowski zurück . Der Trennungssatz von Hahn-Banach verallgemeinert das Ergebnis auf topologische Vektorräume .

Ein verwandtes Ergebnis ist das unterstützende Hyperebenen-Theorem .

Im Kontext von Support-Vektor-Maschinen ist die optimal trennende Hyperebene oder Hyperebene mit maximalem Rand eine Hyperebene, die zwei konvexe Hüllen von Punkten trennt und von beiden gleich weit entfernt ist.

Aussagen und Beweise

Der Beweis basiert auf folgendem Lemma:

Beweis von Lemma : Let Let eine Folge in so dass . Beachten Sie, dass in da konvex ist und so . Schon seit ${\displaystyle \delta =\inf\{|x|:x\in K\}.}$${\displaystyle x_{j}}$${\displaystyle K}$${\displaystyle |x_{j}|\to\delta}$${\displaystyle (x_{i}+x_{j})/2}$${\displaystyle K}$${\displaystyle K}$${\displaystyle |x_{i}+x_{j}|^{2}\geq 4\delta ^{2}}$

${\displaystyle |x_{i}-x_{j}|^{2}=2|x_{i}|^{2}+2|x_{j}|^{2}-|x_{i}+x_ {j}|^{2}\leq 2|x_{i}|^{2}+2|x_{j}|^{2}-4\delta ^{2}\to 0}$

als , eine Cauchy - Folge und so hat Grenze x in . Sie ist eindeutig, denn wenn y in ist und die Norm δ hat, dann gilt und x = y .${\displaystyle i,j\to\infty}$${\displaystyle x_{i}}$${\displaystyle K}$${\displaystyle K}$${\displaystyle |xy|^{2}\leq 2|x|^{2}+2|y|^{2}-4\delta ^{2}=0}$${\displaystyle \square}$

Beweis des Satzes : Gegeben disjunkte nichtleere konvexe Mengen A , B , sei

${\displaystyle K=A+(-B)=\{xy\mid x\in A,y\in B\}.}$

Da konvex ist und die Summe der konvexen Mengen konvex ist, ist konvex. Nach dem Lemma enthält der Abschluss von , der konvex ist, einen Vektor minimaler Norm. Da für jedes in konvex ist , ist das Geradensegment ${\displaystyle -B}$${\displaystyle K}$${\displaystyle {\overline {K}}}$${\displaystyle K}$${\displaystyle v}$${\displaystyle {\overline {K}}}$${\displaystyle n}$${\displaystyle K}$

${\displaystyle v+t(nv),\,0\leq t\leq 1}$

liegt drin und so ${\displaystyle {\overline {K}}}$

${\displaystyle |v|^{2}\leq |v+t(nv)|^{2}=|v|^{2}+2t\langle v,nv\rangle +t^{2}|nv| ^{2}}$.

Für haben wir also: ${\displaystyle 0<t\leq 1}$

${\displaystyle 0\leq 2\langle v,n\rangle -2|v|^{2}+t|nv|^{2}}$

und lassen gibt: . Daher gilt für jedes x in A und y in B : . Wenn also v ungleich Null ist, ist der Beweis vollständig, da ${\displaystyle t\to 0}$${\displaystyle \langle n,v\rangle\geq |v|^{2}}$${\displaystyle \langle xy,v\rangle\geq |v|^{2}}$

${\displaystyle \inf_{x\in A}\langle x,v\rangle \geq |v|^{2}+\sup_{y\in B}\langle y,v\rangle.}$

Allgemeiner (für den Fall v = 0) nehmen wir zunächst den Fall, dass das Innere von nicht leer ist. Das Innere kann durch eine verschachtelte Folge von nichtleeren kompakten konvexen Teilmengen (nämlich put ) erschöpft werden . Da 0 nicht in ist , enthält jeder einen von Null verschiedenen Vektor minimaler Länge und nach dem Argument im ersten Teil haben wir: für jeden . Wir können die 's so normalisieren , dass sie die Länge eins haben. Dann enthält die Folge eine konvergente Teilfolge (weil die n-Sphäre kompakt ist) mit Grenzwert v , der von Null verschieden ist. Wir haben für jedes x im Inneren von und durch Stetigkeit gilt dasselbe für alle x in . Wir beenden nun den Beweis wie zuvor. Wenn es schließlich einen leeren Innenraum hat, hat die affine Menge , die es umspannt, eine Dimension, die kleiner ist als die des gesamten Raums. Folglich ist in einer Hyperebene enthalten ; also für alle x in und wir beenden den Beweis wie zuvor.${\displaystyle K}$${\displaystyle K_{1}\subset K_{2}\subset K_{3}\subset \cdots}$${\displaystyle K_{j}\equiv [-j,j]^{n}\cap \{x\in {\text{int}}(K):d(x,({\text{int}}( K))^{c})\geq {\frac {1}{j}}\}}$${\displaystyle K}$${\displaystyle K_{n}}$${\displaystyle v_{n}}$${\displaystyle \langle x,v_{n}\rangle \geq 0}$${\displaystyle x\in K_{n}}$${\displaystyle v_{n}}$${\displaystyle v_{n}}$${\displaystyle\langle x,v\rangle\geq 0}$${\displaystyle K}$${\displaystyle K}$${\displaystyle K}$${\displaystyle K}$${\displaystyle \langle \cdot ,v\rangle =c}$${\displaystyle \langle x,v\rangle \geq c}$${\displaystyle K}$${\displaystyle \square}$

Die Anzahl der Dimensionen muss endlich sein. In unendlichdimensionalen Räumen gibt es Beispiele für zwei geschlossene, konvexe, disjunkte Mengen, die nicht durch eine geschlossene Hyperebene (eine Hyperebene, in der ein stetiges lineares Funktional einer Konstanten entspricht) getrennt werden können, selbst im schwachen Sinne, wo die Ungleichungen nicht streng sind.

Der obige Beweis beweist auch die erste Version des in der Lede erwähnten Satzes (um es zu sehen, beachten Sie, dass der Beweis unter der Hypothese des folgenden Satzes abgeschlossen ist.) ${\displaystyle K}$

Hier kann die Kompaktheit der Hypothese nicht gelockert werden; siehe ein Beispiel im nächsten Abschnitt. Diese Version des Trennungssatzes verallgemeinert sich auf unendliche Dimensionen; die Verallgemeinerung ist häufiger als Hahn-Banach-Trennungssatz bekannt .

Wir haben auch:

Dies folgt aus der Standardversion, da die trennende Hyperebene das Innere der konvexen Mengen nicht schneiden kann.

Umkehrung des Satzes

Beachten Sie, dass die Existenz einer Hyperebene, die nur zwei konvexe Mengen im schwachen Sinne "trennt", dass beide Ungleichungen nicht streng sind, offensichtlich nicht impliziert, dass die beiden Mengen disjunkt sind. Beide Sätze könnten Punkte haben, die sich auf der Hyperebene befinden.

Gegenbeispiele und Einzigartigkeit

Wenn eines von A oder B nicht konvex ist, gibt es viele mögliche Gegenbeispiele. Zum Beispiel A und B könnten konzentrische Kreise sein. Ein subtileres Gegenbeispiel ist eines, in dem A und B beide abgeschlossen sind, aber keines davon kompakt ist. Wenn beispielsweise A eine geschlossene Halbebene ist und B von einem Arm einer Hyperbel begrenzt wird, dann gibt es keine streng trennende Hyperebene:

${\displaystyle A=\{(x,y):x\leq 0\}}$

${\displaystyle B=\{(x,y):x>0,y\geq 1/x\}.\ }$

(Obwohl es nach einer Instanz des zweiten Satzes eine Hyperebene gibt, die ihr Inneres trennt.) Eine andere Art von Gegenbeispiel hat A kompakt und B offen. Zum Beispiel kann A ein geschlossenes Quadrat sein und B kann ein offenes Quadrat sein, das A berührt .

In der ersten Version des Theorems ist die trennende Hyperebene offensichtlich nie eindeutig. In der zweiten Version kann es eindeutig sein oder nicht. Technisch gesehen ist eine Trennachse nie eindeutig, weil sie verschoben werden kann; in der zweiten Version des Theorems kann eine Trennachse bis auf die Translation eindeutig sein.

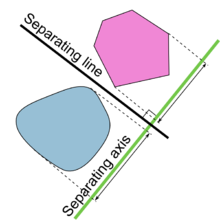
Verwendung bei der Kollisionserkennung

Der Trennachsensatz (SAT) besagt:

Zwei konvexe Objekte überlappen sich nicht, wenn eine Linie (als Achse bezeichnet) existiert, auf der sich die Projektionen der beiden Objekte nicht überlappen.

SAT schlägt einen Algorithmus vor, um zu testen, ob sich zwei konvexe Körper schneiden oder nicht.

Unabhängig von der Dimensionalität ist die Trennachse immer eine Linie. In 3D ist der Raum beispielsweise durch Ebenen getrennt, die Trennachse steht jedoch senkrecht zur Trennebene.

Das Trennachsentheorem kann zur schnellen Kollisionserkennung zwischen Polygonnetzen angewendet werden . Die Normalen- oder andere Feature-Richtung jeder Fläche wird als Trennachse verwendet. Beachten Sie, dass dies mögliche Trennachsen ergibt, keine Trennlinien/Ebenen.

In 3D kann die alleinige Verwendung von Flächennormalen einige nicht kollidierende Fälle von Kante zu Kante nicht trennen. Es werden zusätzliche Achsen benötigt, die aus den Kreuzprodukten von Kantenpaaren bestehen, eine von jedem Objekt genommen.

Zur Erhöhung der Effizienz können parallele Achsen als eine einzige Achse berechnet werden.

Siehe auch

• Doppelkegel
• Farkas Lemma
• Satz von Kirchberger
• Optimale Kontrolle

Anmerkungen

Verweise

• Boyd, Stephen P.; Vandenberghe, Lieven (2004). Konvexe Optimierung (PDF) . Cambridge University Press. ISBN 978-0-521-83378-3.
• Golshtein, EG; Tretjakow, NV (1996). Modifizierte Lagrange- und monotone Karten in der Optimierung . New York: Wiley. P. 6. ISBN 0-471-54821-9.
• Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Nicht differenzierbare und zweistufige mathematische Programmierung . Boston: Kluwer Academic Publishers. P. 19. ISBN 0-7923-9821-1.

Externe Links

• Kollisionserkennung und Reaktion