Lineare Diskriminanzanalyse - Linear discriminant analysis

Die lineare Diskriminanzanalyse ( LDA ), die normale Diskriminanzanalyse ( NDA ) oder die Diskriminanzfunktionsanalyse ist eine Verallgemeinerung der linearen Diskriminanz von Fisher , einer Methode, die in der Statistik und anderen Bereichen verwendet wird, um eine lineare Kombination von Merkmalen zu finden, die zwei oder mehr Klassen charakterisiert oder trennt von Objekten oder Ereignissen. Die resultierende Kombination kann als linearer Klassifikator oder häufiger zur Dimensionsreduktion vor der späteren Klassifizierung verwendet werden .

LDA steht in engem Zusammenhang mit der Varianzanalyse (ANOVA) und der Regressionsanalyse , die ebenfalls versuchen, eine abhängige Variable als Linearkombination anderer Merkmale oder Messwerte auszudrücken . ANOVA verwendet jedoch kategoriale unabhängige Variablen und eine kontinuierliche abhängige Variable , während die Diskriminanzanalyse kontinuierliche unabhängige Variablen und eine kategoriale abhängige Variable ( dh das Klassenlabel) hat. Logistische Regression und Probit-Regression sind LDA ähnlicher als ANOVA, da sie auch eine kategoriale Variable durch die Werte stetiger unabhängiger Variablen erklären. Diese anderen Methoden sind in Anwendungen vorzuziehen, bei denen es nicht sinnvoll ist, anzunehmen, dass die unabhängigen Variablen normalverteilt sind, was eine grundlegende Annahme der LDA-Methode ist.

LDA ist auch eng mit der Hauptkomponentenanalyse (PCA) und der Faktorenanalyse verbunden , da beide nach Linearkombinationen von Variablen suchen, die die Daten am besten erklären. LDA versucht explizit, den Unterschied zwischen den Datenklassen zu modellieren. Im Gegensatz dazu berücksichtigt PCA keine Klassenunterschiede, und die Faktoranalyse erstellt die Merkmalskombinationen basierend auf Unterschieden und nicht auf Ähnlichkeiten. Die Diskriminanzanalyse unterscheidet sich von der Faktorenanalyse auch dadurch, dass sie keine Interdependenztechnik ist: Es muss zwischen unabhängigen Variablen und abhängigen Variablen (auch Kriteriumsvariablen genannt) unterschieden werden.

LDA funktioniert, wenn die Messungen an unabhängigen Variablen für jede Beobachtung kontinuierliche Größen sind. Beim Umgang mit kategorialen unabhängigen Variablen ist die äquivalente Technik die diskriminante Korrespondenzanalyse.

Die Diskriminanzanalyse wird verwendet, wenn Gruppen a priori bekannt sind (im Gegensatz zur Clusteranalyse ). Jeder Fall muss eine Punktzahl für eine oder mehrere quantitative Prädiktorkennzahlen und eine Punktzahl für eine Gruppenkennzahl aufweisen. Vereinfacht ausgedrückt ist die Diskriminanzfunktionsanalyse eine Klassifikation – der Vorgang, Dinge in Gruppen, Klassen oder Kategorien desselben Typs einzuteilen.

Geschichte

Die ursprüngliche dichotome Diskriminanzanalyse wurde 1936 von Sir Ronald Fisher entwickelt . Sie unterscheidet sich von einer ANOVA oder MANOVA , die verwendet wird, um eine (ANOVA) oder mehrere (MANOVA) kontinuierliche abhängige Variablen durch eine oder mehrere unabhängige kategoriale Variablen vorherzusagen. Die Diskriminanzfunktionsanalyse ist nützlich, um zu bestimmen, ob ein Satz von Variablen bei der Vorhersage der Kategoriezugehörigkeit wirksam ist.

LDA für zwei Klassen

Betrachten Sie eine Reihe von Beobachtungen (auch als Merkmale, Attribute, Variablen oder Messungen bezeichnet) für jede Stichprobe eines Objekts oder Ereignisses mit bekannter Klasse . Dieser Satz von Stichproben wird als Trainingssatz bezeichnet . Das Klassifikationsproblem besteht dann darin, einen guten Prädiktor für die Klasse einer beliebigen Stichprobe derselben Verteilung (nicht unbedingt aus dem Trainingssatz) zu finden, wenn nur eine Beobachtung gegeben ist . ${\displaystyle {\vec {x}}}$${\displaystyle y}$${\displaystyle y}$${\displaystyle {\vec {x}}}$

LDA nähert sich das Problem , dass die bedingten Annahme Wahrscheinlichkeitsdichtefunktionen und ist sowohl die Normalverteilung mit dem Mittelwert und Kovarianz - Parametern und sind. Unter dieser Annahme besteht die optimale Bayes-Lösung darin, Punkte als aus der zweiten Klasse zu prognostizieren, wenn der Logarithmus der Likelihood-Verhältnisse größer als ein Schwellenwert T ist, so dass: ${\displaystyle p({\vec {x}}|y=0)}$${\displaystyle p({\vec {x}}|y=1)}$${\displaystyle \left({\vec {\mu}}_{0},\Sigma_{0}\right)}$${\displaystyle \left({\vec {\mu}}_{1},\Sigma_{1}\right)}$

${\displaystyle ({\vec {x}}-{\vec {\mu}}_{0})^{T}\Sigma _{0}^{-1}({\vec {x}}-{ \vec {\mu}}_{0})+\ln |\Sigma_{0}|-({\vec {x}}-{\vec {\mu}}_{1})^{T} \Sigma _{1}^{-1}({\vec {x}}-{\vec {\mu}}_{1})-\ln |\Sigma_{1}|\ >\ T}$

Ohne weitere Annahmen wird der resultierende Klassifikator als QDA ( quadratische Diskriminanzanalyse ) bezeichnet.

LDA macht stattdessen die zusätzliche vereinfachende Annahme der Homoskedastizität ( dh dass die Klassenkovarianzen identisch sind, also ) und dass die Kovarianzen vollen Rang haben. In diesem Fall stornieren mehrere Begriffe: ${\displaystyle \Sigma_{0}=\Sigma_{1}=\Sigma}$

${\displaystyle {\vec {x}}^{T}\Sigma _{0}^{-1}{\vec {x}}={\vec {x}}^{T}\Sigma _{1} ^{-1}{\vec {x}}}$

${\displaystyle {\vec {x}}^{T}{\Sigma_{i}}^{-1}{\vec {\mu}}_{i}={{\vec {\mu}}_ {i}}^{T}{\Sigma_{i}}^{-1}{\vec {x}}}$ weil ist Hermitian${\displaystyle \Sigma_{i}}$

und das obige Entscheidungskriterium wird zu einem Schwellenwert für das Skalarprodukt

${\displaystyle {\vec {w}}\cdot {\vec {x}}>c}$

für eine Schwellenkonstante c , wobei

${\displaystyle {\vec {w}}=\Sigma^{-1}({\vec {\mu}}_{1}-{\vec {\mu}}_{0})}$

${\displaystyle c={\vec {w}}\cdot {\frac {1}{2}}({\vec {\mu}}_{1}+{\vec {\mu}}_{0} )}$

Dies bedeutet, dass das Kriterium der Zugehörigkeit eines Inputs zu einer Klasse rein eine Funktion dieser Linearkombination der bekannten Beobachtungen ist. ${\displaystyle {\vec {x}}}$${\displaystyle y}$

Es ist oft nützlich, diese Schlussfolgerung in geometrischer Hinsicht zu sehen: Das Kriterium, dass eine Eingabe in einer Klasse ist, ist eine reine Funktion der Projektion des mehrdimensionalen Raumpunktes auf den Vektor (also betrachten wir nur seine Richtung). Mit anderen Worten, die Beobachtung gehört zu, wenn sich die entsprechende auf einer bestimmten Seite einer Hyperebene senkrecht zu befindet . Die Lage der Ebene wird durch den Schwellenwert c definiert. ${\displaystyle {\vec {x}}}$${\displaystyle y}$${\displaystyle {\vec {x}}}$${\displaystyle {\vec {w}}}$${\displaystyle y}$${\displaystyle {\vec {x}}}$${\displaystyle {\vec {w}}}$

Annahmen

Die Annahmen der Diskriminanzanalyse sind die gleichen wie bei der MANOVA. Die Analyse reagiert sehr empfindlich auf Ausreißer und die Größe der kleinsten Gruppe muss größer sein als die Anzahl der Prädiktorvariablen.

• Multivariate Normalität : Unabhängige Variablen sind für jede Ebene der Gruppierungsvariablen normal.
• Homogenität der Varianz/Kovarianz ( Homoskedastizität ): Die Varianzen zwischen den Gruppenvariablen sind über die Prädiktorenebenen hinweg gleich. Kann mit der M- Statistik von Box getestet werden . Es wurde jedoch vorgeschlagen, dass die lineare Diskriminanzanalyse verwendet wird, wenn die Kovarianzen gleich sind, und dass die quadratische Diskriminanzanalyse verwendet werden kann, wenn die Kovarianzen nicht gleich sind.
• Multikollinearität : Die Vorhersagekraft kann mit einer erhöhten Korrelation zwischen Prädiktorvariablen abnehmen.
• Unabhängigkeit : Es wird davon ausgegangen, dass die Teilnehmer zufällig ausgewählt wurden, und es wird angenommen, dass die Punktzahl eines Teilnehmers bei einer Variablen unabhängig von den Bewertungen dieser Variablen für alle anderen Teilnehmer ist.

Es wurde vorgeschlagen, dass die Diskriminanzanalyse relativ robust gegenüber leichten Verletzungen dieser Annahmen ist, und es wurde auch gezeigt, dass die Diskriminanzanalyse immer noch zuverlässig sein kann, wenn dichotome Variablen verwendet werden (bei denen die multivariate Normalität oft verletzt wird).

Diskriminierende Funktionen

Die Diskriminanzanalyse funktioniert, indem eine oder mehrere lineare Kombinationen von Prädiktoren erstellt werden, wodurch für jede Funktion eine neue latente Variable erstellt wird . Diese Funktionen werden Diskriminanzfunktionen genannt. Die Anzahl der Funktionen möglich ist , entweder in dem = Anzahl der Gruppen, oder (die Anzahl der Prädiktoren), je nachdem , was kleiner ist . Die erste erstellte Funktion maximiert die Unterschiede zwischen den Gruppen dieser Funktion. Die zweite Funktion maximiert die Unterschiede dieser Funktion, darf aber auch nicht mit der vorherigen Funktion korreliert werden. Dies setzt sich mit nachfolgenden Funktionen fort, mit der Anforderung, dass die neue Funktion nicht mit einer der vorherigen Funktionen korreliert. ${\displaystyle N_{g}-1}$${\displaystyle N_{g}}$${\displaystyle p}$

Gegebene Gruppe mit Mengen von Stichprobenräumen gibt es eine Diskriminanzregel, so dass wenn , dann . Die Diskriminanzanalyse findet dann „gute“ Bereiche, um Klassifikationsfehler zu minimieren, und führt daher zu einem hohen Prozentsatz richtiger Klassifikation in der Klassifikationstabelle. ${\displaystyle j}$${\displaystyle \mathbb{R}_{j}}$${\displaystyle x\in\mathbb{R}_{j}}$${\displaystyle x\in j}$${\displaystyle \mathbb{R}_{j}}$

Jede Funktion erhält eine Diskriminanzbewertung, um zu bestimmen, wie gut sie die Gruppenplatzierung vorhersagt.

• Strukturkorrelationskoeffizienten: Die Korrelation zwischen jedem Prädiktor und dem Diskriminanzwert jeder Funktion. Dies ist eine Korrelation nullter Ordnung (dh nicht für die anderen Prädiktoren korrigiert).
• Standardisierte Koeffizienten: Das Gewicht jedes Prädiktors in der Linearkombination, die die Diskriminanzfunktion ist. Wie in einer Regressionsgleichung sind diese Koeffizienten partiell (dh um die anderen Prädiktoren korrigiert). Gibt den eindeutigen Beitrag jedes Prädiktors zur Vorhersage der Gruppenzuordnung an.
• Funktionen an Gruppenschwerpunkten: Für jede Funktion werden mittlere Diskriminanzwerte für jede Gruppierungsvariable angegeben. Je weiter die Mittelwerte auseinander liegen, desto weniger Fehler treten bei der Klassifizierung auf.

Diskriminierungsregeln

• Maximale Wahrscheinlichkeit : Weist x der Gruppe zu, die die Bevölkerungsdichte (Gruppendichte) maximiert.
• Bayes-Diskriminanzregel: Weist x der Gruppe zu, die maximiert , wobei π _i die vorherige Wahrscheinlichkeit dieser Klassifizierung darstellt und die Bevölkerungsdichte darstellt.${\displaystyle \pi_{i}f_{i}(x)}$${\displaystyle f_{i}(x)}$
• Fishers lineare Diskriminanzregel : Maximiert das Verhältnis zwischen SS _zwischen und SS _innerhalb und findet eine Linearkombination der Prädiktoren, um die Gruppe vorherzusagen.

Eigenwerte

Ein Eigenwert in der Diskriminanzanalyse ist die charakteristische Wurzel jeder Funktion. Es ist ein Hinweis darauf, wie gut diese Funktion die Gruppen unterscheidet, wobei die Funktion umso besser differenziert, je größer der Eigenwert ist. Dies ist jedoch mit Vorsicht zu interpretieren, da Eigenwerte keine Obergrenze haben. Der Eigenwert kann als Verhältnis von SS _zwischen und SS _innerhalb wie bei der ANOVA betrachtet werden, wenn die abhängige Variable die Diskriminanzfunktion ist und die Gruppen die Niveaus von IV sind . Dies bedeutet, dass der größte Eigenwert der ersten Funktion zugeordnet ist, der zweitgrößte der zweiten usw.

Effektgröße

Einige schlagen die Verwendung von Eigenwerten als Effektstärkenmaß vor , dies wird jedoch im Allgemeinen nicht unterstützt. Stattdessen ist die kanonische Korrelation das bevorzugte Maß für die Effektstärke. Er ähnelt dem Eigenwert, ist aber die Quadratwurzel des Verhältnisses von SS _zwischen und SS _total . Es ist die Korrelation zwischen Gruppen und der Funktion. Ein weiteres beliebtes Maß für die Effektstärke ist der Prozentsatz der Varianz für jede Funktion. Dies wird wie folgt berechnet: ( λ _x / Σλ _i ) X 100 , wobei λ _x ist der Eigenwert für die Funktion und Σ & lgr; _i die Summe aller Eigenwerte ist. Dies sagt uns, wie stark die Vorhersage für diese bestimmte Funktion im Vergleich zu den anderen ist. Prozent richtig klassifiziert kann auch als Effektstärke analysiert werden. Der Kappa-Wert kann dies beschreiben, während er um zufällige Übereinstimmung korrigiert wird. Kappa normalisiert sich über alle Kategorisierungen hinweg, anstatt durch eine signifikant gute oder schlecht abschneidende Klasse voreingenommen zu sein.

Kanonische Diskriminanzanalyse für k Klassen

Die kanonische Diskriminanzanalyse (CDA) findet Achsen ( k  − 1 kanonische Koordinaten , k ist die Anzahl der Klassen), die die Kategorien am besten trennen. Diese linearen Funktionen sind unkorreliert und definieren effektiv einen optimalen k  − 1-Raum durch die n- dimensionale Datenwolke, die (die Projektionen in diesem Raum von) die k Gruppen am besten trennt . Siehe " Multiclass LDA " für Details weiter unten.

Lineare Diskriminante nach Fisher

Die Begriffe Fishers lineare Diskriminanzanalyse und LDA werden häufig synonym verwendet, obwohl Fishers Original - Artikel beschreibt eigentlich eine etwas andere Diskriminanten, die einige der Annahmen von LDA wie macht nicht normalverteilt Klassen oder gleich Klasse Kovarianzen .

Angenommen, zwei Klassen von Beobachtungen haben Mittelwerte und Kovarianzen . Dann wird die lineare Kombination von Merkmalen haben Mittel und Varianzen für . Fisher definierte die Trennung zwischen diesen beiden Verteilungen als das Verhältnis der Varianz zwischen den Klassen zur Varianz innerhalb der Klassen: ${\displaystyle {\vec {\mu}}_{0},{\vec {\mu}}_{1}}$${\displaystyle \Sigma_{0},\Sigma_{1}}$${\displaystyle {\vec {w}}\cdot {\vec {x}}}$ ${\displaystyle {\vec {w}}\cdot {\vec {\mu}}_{i}}$ ${\displaystyle {\vec {w}}^{T}\Sigma _{i}{\vec {w}}}$${\displaystyle i=0,1}$

${\displaystyle S={\frac {\sigma_{\text{zwischen}}^{2}}{\sigma_{\text{innerhalb}}^{2}}}={\frac {({\vec {w}}\cdot {\vec {\mu}}_{1}-{\vec {w}}\cdot {\vec {\mu}}_{0})^{2}}{{\vec {w}}^{T}\Sigma_{1}{\vec {w}}+{\vec {w}}^{T}\Sigma_{0}{\vec {w}}}}={ \frac {({\vec {w}}\cdot ({\vec {\mu}}_{1}-{\vec {\mu}}_{0}))^{2}}{{\vec {w}}^{T}(\Sigma_{0}+\Sigma_{1}){\vec {w}}}}}$

Dieses Maß ist gewissermaßen ein Maß für das Signal-Rausch-Verhältnis für die Klassenkennzeichnung. Es kann gezeigt werden, dass die maximale Trennung auftritt, wenn

${\displaystyle {\vec {w}}\propto (\Sigma_{0}+\Sigma_{1})^{-1}({\vec {\mu}}_{1}-{\vec { \mu}}_{0})}$

Wenn die Annahmen von LDA erfüllt sind, ist die obige Gleichung äquivalent zu LDA.

Beachten Sie, dass der Vektor die Normale zur diskriminanten Hyperebene ist . Beispielsweise ist in einem zweidimensionalen Problem die Linie, die die beiden Gruppen am besten teilt, senkrecht zu . ${\displaystyle {\vec {w}}}$${\displaystyle {\vec {w}}}$

Im Allgemeinen werden die zu unterscheidenden Datenpunkte auf projiziert ; dann wird der Schwellenwert, der die Daten am besten trennt, aus der Analyse der eindimensionalen Verteilung ausgewählt. Es gibt keine allgemeine Regel für den Schwellenwert. Wenn Projektionen von Punkten aus beiden Klassen jedoch ungefähr die gleichen Verteilungen aufweisen, wäre eine gute Wahl die Hyperebene zwischen den Projektionen der beiden Mittelwerte und . In diesem Fall kann der Parameter c in der Schwellenbedingung explizit gefunden werden: ${\displaystyle {\vec {w}}}$${\displaystyle {\vec {w}}\cdot {\vec {\mu}}_{0}}$${\displaystyle {\vec {w}}\cdot {\vec {\mu}}_{1}}$${\displaystyle {\vec {w}}\cdot {\vec {x}}>c}$

${\displaystyle c={\vec {w}}\cdot {\frac {1}{2}}({\vec {\mu}}_{0}+{\vec {\mu}}_{1} )={\frac{1}{2}}{\vec {\mu}}_{1}^{T}\Sigma_{1}^{-1}{\vec {\mu}}_{1 }-{\frac {1}{2}}{\vec {\mu}}_{0}^{T}\Sigma _{0}^{-1}{\vec {\mu}}_{0 }}$.

Die Methode von Otsu ist mit der linearen Diskriminante von Fisher verwandt und wurde entwickelt, um das Histogramm von Pixeln in einem Graustufenbild durch optimale Auswahl des Schwarz/Weiß-Schwellenwerts zu binarisieren, der die Varianz innerhalb der Klasse minimiert und die Varianz zwischen den Klassen innerhalb/zwischen den Graustufen, die Schwarz und zugewiesen sind, maximiert weiße Pixelklassen.

Mehrklassen-LDA

Im Fall von mehr als zwei Klassen kann die bei der Ableitung der Fisher-Diskriminante verwendete Analyse erweitert werden, um einen Unterraum zu finden , der die gesamte Klassenvariabilität zu enthalten scheint. Diese Verallgemeinerung ist auf CR Rao zurückzuführen . Angenommen, jede der C-Klassen hat einen Mittelwert und dieselbe Kovarianz . Dann kann die Streuung zwischen der Klassenvariabilität durch die Stichprobenkovarianz der Klassenmittelwerte definiert werden ${\displaystyle \mu_{i}}$${\displaystyle \Sigma}$

${\displaystyle \Sigma_{b}={\frac{1}{C}}\sum_{i=1}^{C}(\mu_{i}-\mu)(\mu_{i} -\mu)^{T}}$

wo ist der Mittelwert der Klassenmittelwerte. Die Klassentrennung in eine Richtung ist in diesem Fall gegeben durch ${\displaystyle\mu}$${\displaystyle {\vec {w}}}$

${\displaystyle S={\frac {{\vec {w}}^{T}\Sigma _{b}{\vec {w}}}{{\vec {w}}^{T}\Sigma {\ vec {w}}}}}$

Dies bedeutet , dass , wenn eine ist Eigenvektor von der Trennung wird in dem entsprechenden gleich seinen Eigenwerte . ${\displaystyle {\vec {w}}}$${\displaystyle \Sigma^{-1}\Sigma_{b}}$

Wenn diagonalisierbar ist, wird die Variabilität zwischen Merkmalen in dem Unterraum enthalten sein, der von den Eigenvektoren aufgespannt wird, die den C  − 1 größten Eigenwerten entsprechen (da  höchstens den Rang C − 1 hat). Diese Eigenvektoren werden hauptsächlich bei der Merkmalsreduktion verwendet, wie bei der PCA. Die Eigenvektoren, die den kleineren Eigenwerten entsprechen, neigen dazu, sehr empfindlich auf die genaue Wahl der Trainingsdaten zu reagieren, und es ist oft notwendig, eine Regularisierung zu verwenden, wie im nächsten Abschnitt beschrieben. ${\displaystyle \Sigma^{-1}\Sigma_{b}}$${\displaystyle \Sigma_{b}}$

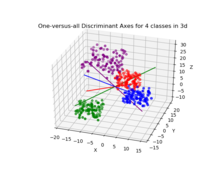
Wenn eine Klassifizierung erforderlich ist, stehen anstelle einer Dimensionsreduktion eine Reihe alternativer Techniken zur Verfügung. Zum Beispiel können die Klassen partitioniert werden und eine Standard-Fischer-Diskriminante oder LDA verwendet werden, um jede Partition zu klassifizieren. Ein gängiges Beispiel dafür ist "Einer gegen den Rest", bei dem die Punkte einer Klasse in eine Gruppe und alles andere in die andere Gruppe gelegt werden und dann die LDA angewendet wird. Dies führt zu C-Klassifikatoren, deren Ergebnisse kombiniert werden. Eine weitere gängige Methode ist die paarweise Klassifikation, bei der für jedes Klassenpaar ein neuer Klassifikator erstellt wird (insgesamt C ( C  − 1)/2 Klassifikatoren), wobei die einzelnen Klassifikatoren zu einer endgültigen Klassifikation kombiniert werden.

Inkrementelles LDA

Die typische Implementierung der LDA-Technik erfordert, dass alle Proben im Voraus verfügbar sind. Es gibt jedoch Situationen, in denen nicht der gesamte Datensatz verfügbar ist und die Eingabedaten als Stream betrachtet werden. In diesem Fall ist es wünschenswert, dass die LDA-Merkmalsextraktion die Fähigkeit hat, die berechneten LDA-Merkmale durch Beobachten der neuen Abtastwerte zu aktualisieren, ohne den Algorithmus für den gesamten Datensatz auszuführen. In vielen Echtzeitanwendungen wie der mobilen Robotik oder der Online-Gesichtserkennung ist es beispielsweise wichtig, die extrahierten LDA-Merkmale zu aktualisieren, sobald neue Beobachtungen verfügbar sind. Eine LDA-Merkmalsextraktionstechnik, die die LDA-Merkmale durch einfaches Beobachten neuer Stichproben aktualisieren kann, ist ein inkrementeller LDA-Algorithmus , und diese Idee wurde in den letzten zwei Jahrzehnten ausgiebig untersucht. Chatterjee und Roychowdhury schlugen einen inkrementellen selbstorganisierten LDA-Algorithmus zur Aktualisierung der LDA-Funktionen vor. In einer anderen Arbeit schlugen Demir und Ozmehmet lokale Online-Lernalgorithmen zur schrittweisen Aktualisierung von LDA-Funktionen unter Verwendung von Fehlerkorrektur und den hebbianischen Lernregeln vor. Später haben Aliyari et al . abgeleitete schnelle inkrementelle Algorithmen, um die LDA-Merkmale durch Beobachten der neuen Stichproben zu aktualisieren.

Praktischer Nutzen

In der Praxis sind die Klassenmittelwerte und Kovarianzen nicht bekannt. Sie können jedoch aus dem Trainingssatz geschätzt werden. Anstelle des exakten Wertes in den obigen Gleichungen kann entweder die maximale Wahrscheinlichkeitsschätzung oder die maximale a-posteriori- Schätzung verwendet werden. Obwohl die Schätzungen der Kovarianz in gewissem Sinne als optimal angesehen werden können, bedeutet dies nicht, dass die resultierende Diskriminante, die durch Ersetzen dieser Werte erhalten wird, in irgendeiner Weise optimal ist, selbst wenn die Annahme normalverteilter Klassen richtig ist.

Eine weitere Komplikation bei der Anwendung von LDA und Fisher's Diskriminante auf reale Daten tritt auf, wenn die Anzahl der Messungen jedes Samples (dh die Dimensionalität jedes Datenvektors) die Anzahl der Samples in jeder Klasse überschreitet. In diesem Fall haben die Kovarianzschätzungen keinen vollen Rang und können daher nicht invertiert werden. Es gibt eine Reihe von Möglichkeiten, damit umzugehen. Eine besteht darin, in den obigen Formeln eine Pseudo-Inverse anstelle der üblichen Matrix-Inversen zu verwenden. Eine bessere numerische Stabilität kann jedoch erreicht werden, indem das Problem zunächst auf den von aufgespannten Unterraum projiziert wird . Eine andere Strategie zum Umgang mit kleinen Stichproben ist die Verwendung eines Schrumpfungsschätzers der Kovarianzmatrix, der mathematisch ausgedrückt werden kann als ${\displaystyle \Sigma_{b}}$

${\displaystyle \Sigma =(1-\lambda)\Sigma +\lambda I\,}$

wobei ist die Identitätsmatrix und ist die Schrumpfungsintensität oder der Regularisierungsparameter . Dies führt zum Rahmen der regularisierten Diskriminanzanalyse oder der Schrumpfungs-Diskriminanzanalyse. ${\displaystyle I}$${\displaystyle \lambda}$

Außerdem sind in vielen praktischen Fällen lineare Diskriminanten nicht geeignet. LDA und Fisher's Diskriminante können über den Kernel-Trick zur Verwendung in der nichtlinearen Klassifikation erweitert werden . Hier werden die ursprünglichen Beobachtungen effektiv in einen höherdimensionalen nichtlinearen Raum abgebildet. Die lineare Klassifikation in diesem nichtlinearen Raum entspricht dann der nichtlinearen Klassifikation im ursprünglichen Raum. Das am häufigsten verwendete Beispiel dafür ist die Kernel-Fischer-Diskriminante .

LDA kann zu einer multiplen Diskriminanzanalyse verallgemeinert werden , wobei c eine kategoriale Variable mit N möglichen Zuständen anstelle von nur zwei wird. Analog dazu, wenn die klassenbedingten Dichten mit geteilten Kovarianzen normal sind, ist die ausreichende Statistik für die Werte von N Projektionen, die der von den N Mittelwerten aufgespannte Unterraum sind, affin projiziert durch die inverse Kovarianzmatrix. Diese Projektionen können durch Lösen eines verallgemeinerten Eigenwertproblems gefunden werden , wobei der Zähler die Kovarianzmatrix ist, die durch Behandlung der Mittelwerte als Stichproben gebildet wird, und der Nenner die gemeinsame Kovarianzmatrix ist. Weitere Informationen finden Sie oben unter „ Mehrklassen-LDA “. ${\displaystyle p({\vec {x}}\mid c=i)}$${\displaystyle P(c\mid {\vec {x}})}$

Anwendungen

Zusätzlich zu den unten aufgeführten Beispielen wird LDA in der Positionierung und im Produktmanagement eingesetzt .

Insolvenzvorhersage

Bei der Konkursvorhersage auf der Grundlage von Bilanzierungskennzahlen und anderen Finanzvariablen war die lineare Diskriminanzanalyse die erste statistische Methode, die angewendet wurde, um systematisch zu erklären, welche Unternehmen in Konkurs gegangen sind oder welche Firmen überlebt haben. Trotz Einschränkungen einschließlich bekannten nonconformance von Verhältnissen zu den normalen Verteilungsannahmen von LDA Buchhaltung, Edward Altman ‚s 1968 - Modell ist nach wie vor eine führende Modell in der Praxis.

Gesichtserkennung

Bei der computergestützten Gesichtserkennung wird jedes Gesicht durch eine große Anzahl von Pixelwerten dargestellt. Die lineare Diskriminanzanalyse wird hier hauptsächlich verwendet, um die Anzahl der Merkmale vor der Klassifizierung auf eine überschaubarere Anzahl zu reduzieren. Jede der neuen Dimensionen ist eine lineare Kombination von Pixelwerten, die eine Vorlage bilden. Die mit der linearen Diskriminante von Fisher erhaltenen Linearkombinationen werden als Fisher-Gesichter bezeichnet , während diejenigen, die mit der zugehörigen Hauptkomponentenanalyse erhalten werden, als Eigengesichter bezeichnet werden .

Marketing

Im Marketing wurde die Diskriminanzanalyse früher oft verwendet, um anhand von Umfragen oder anderen erhobenen Daten die Faktoren zu bestimmen, die verschiedene Kundentypen und/oder Produkte unterscheiden. Logistische Regression oder andere Methoden werden jetzt häufiger verwendet. Der Einsatz der Diskriminanzanalyse im Marketing lässt sich durch folgende Schritte beschreiben:

1. Formulieren Sie das Problem und sammeln Sie Daten – Identifizieren Sie die hervorstechenden Attribute, die Verbraucher zur Bewertung von Produkten in dieser Kategorie verwenden – Verwenden Sie quantitative Marktforschungstechniken (wie Umfragen ), um Daten von einer Stichprobe potenzieller Kunden zu deren Bewertungen aller Produktattribute zu sammeln. Die Datenerhebungsphase wird normalerweise von Marktforschungsexperten durchgeführt. Bei Umfragefragen wird der Befragte aufgefordert, ein Produkt anhand einer Reihe von Attributen, die der Forscher ausgewählt hat, mit eins bis fünf (oder 1 bis 7 oder 1 bis 10) zu bewerten. Es werden zwischen fünf und zwanzig Attribute ausgewählt. Dazu gehören beispielsweise: Benutzerfreundlichkeit, Gewicht, Genauigkeit, Haltbarkeit, Farbigkeit, Preis oder Größe. Die ausgewählten Attribute variieren je nach untersuchtem Produkt. Die gleiche Frage wird zu allen Produkten in der Studie gestellt. Die Daten für mehrere Produkte werden kodiert und in ein Statistikprogramm wie R , SPSS oder SAS eingegeben . (Dieser Schritt ist der gleiche wie bei der Faktorenanalyse).
2. Schätzen Sie die Diskriminanzfunktionskoeffizienten und bestimmen Sie die statistische Signifikanz und Validität – Wählen Sie die geeignete Diskriminanzanalysemethode. Bei der direkten Methode wird die Diskriminanzfunktion geschätzt, so dass alle Prädiktoren gleichzeitig bewertet werden. Bei der schrittweisen Methode werden die Prädiktoren sequentiell eingegeben. Die Zweigruppenmethode sollte verwendet werden, wenn die abhängige Variable zwei Kategorien oder Zustände aufweist. Die multiple Diskriminanzmethode wird verwendet, wenn die abhängige Variable drei oder mehr kategoriale Zustände aufweist. Verwenden Sie Wilks's Lambda , um die Signifikanz in SPSS oder F-Stat in SAS zu testen. Die gebräuchlichste Methode zum Testen der Validität besteht darin, die Stichprobe in eine Schätzungs- oder Analysestichprobe und eine Validierungs- oder Holdout-Stichprobe aufzuteilen. Die Schätzungsstichprobe wird beim Konstruieren der Diskriminanzfunktion verwendet. Aus der Validierungsstichprobe wird eine Klassifikationsmatrix erstellt, die die Anzahl der richtig klassifizierten und falsch klassifizierten Fälle enthält. Der Prozentsatz der richtig klassifizierten Fälle wird als Trefferquote bezeichnet .
3. Zeichnen Sie die Ergebnisse auf einer zweidimensionalen Karte, definieren Sie die Dimensionen und interpretieren Sie die Ergebnisse. Das Statistikprogramm (oder ein verwandtes Modul) bildet die Ergebnisse ab. Die Karte zeichnet jedes Produkt (normalerweise im zweidimensionalen Raum) auf. Der Abstand der Produkte zueinander gibt an, wie unterschiedlich sie sind. Die Maße müssen vom Forscher beschriftet werden. Dies erfordert subjektives Urteilsvermögen und ist oft sehr anspruchsvoll. Siehe Wahrnehmungszuordnung .

Biomedizinische Studien

Die Hauptanwendung der Diskriminanzanalyse in der Medizin ist die Beurteilung des Schweregrads eines Patienten und die Prognose des Krankheitsverlaufs. Bei der retrospektiven Analyse werden die Patienten beispielsweise nach Schweregrad der Erkrankung in Gruppen eingeteilt – leichte, mittelschwere und schwere Form. Anschließend werden die Ergebnisse klinischer und Laboranalysen untersucht, um Variablen aufzudecken, die sich in den untersuchten Gruppen statistisch unterscheiden. Unter Verwendung dieser Variablen werden Diskriminanzfunktionen erstellt, die helfen, die Krankheit eines zukünftigen Patienten objektiv in leichte, mittelschwere oder schwere Form zu klassifizieren.

In der Biologie werden ähnliche Prinzipien verwendet, um Gruppen verschiedener biologischer Objekte zu klassifizieren und zu definieren, zum Beispiel um Phagentypen von Salmonella enteritidis basierend auf Fourier-Transformations-Infrarotspektren zu definieren, um tierische Quellen von Escherichia coli durch Untersuchung seiner Virulenzfaktoren zu erkennen usw.

Erdkunde

Diese Methode kann verwendet werden, um die Änderungszonen zu trennen . Wenn beispielsweise unterschiedliche Daten aus verschiedenen Zonen verfügbar sind, kann die Diskriminanzanalyse das Muster in den Daten finden und es effektiv klassifizieren.

Vergleich zur logistischen Regression

Die Diskriminanzfunktionsanalyse ist der logistischen Regression sehr ähnlich , und beide können verwendet werden, um dieselben Forschungsfragen zu beantworten. Die logistische Regression hat nicht so viele Annahmen und Einschränkungen wie die Diskriminanzanalyse. Wenn jedoch die Annahmen der Diskriminanzanalyse erfüllt sind, ist sie leistungsfähiger als die logistische Regression. Im Gegensatz zur logistischen Regression kann die Diskriminanzanalyse mit kleinen Stichprobengrößen verwendet werden. Es hat sich gezeigt, dass bei gleichen Stichprobengrößen und Homogenität der Varianz/Kovarianz die Diskriminanzanalyse genauer ist. Trotz all dieser Vorteile hat sich die logistische Regression dennoch durchgesetzt, da die Annahmen der Diskriminanzanalyse selten erfüllt werden.

Lineare Diskriminante in hoher Dimension

Geometrische Anomalien in hoher Dimension führen zum bekannten Fluch der Dimensionalität . Dennoch kann die richtige Nutzung der Konzentration von Messphänomenen die Berechnung erleichtern. Ein wichtiger Fall dieses Segens der Dimensionalitätsphänomene wurde von Donoho und Tanner hervorgehoben: Wenn eine Stichprobe im Wesentlichen hochdimensional ist, kann jeder Punkt mit hoher Wahrscheinlichkeit auch bei exponentiell großen Stichproben durch lineare Ungleichung vom Rest der Stichprobe getrennt werden. Diese linearen Ungleichungen können in der Standardform (Fishers) der linearen Diskriminante für eine reiche Familie von Wahrscheinlichkeitsverteilungen ausgewählt werden. Insbesondere sind solche Sätze für log-konkave Verteilungen einschließlich mehrdimensionaler Normalverteilung (der Beweis basiert auf den Konzentrationsungleichungen für log-konkave Maße) und für Produktmaße auf einem mehrdimensionalen Würfel (bewiesen mit der Konzentrationsungleichung von Talagrand für die Produktwahrscheinlichkeit) Leerzeichen). Die Datentrennbarkeit durch klassische lineare Diskriminanten vereinfacht das Problem der Fehlerkorrektur für Systeme der künstlichen Intelligenz in hoher Dimension.

Siehe auch

• Data-Mining
• Entscheidungsbaum lernen
• Faktorenanalyse
• Kernel Fisher Diskriminanzanalyse
• Logit (für logistische Regression )
• Lineare Regression
• Multiple Diskriminanzanalyse
• Mehrdimensionale Skalierung
• Mustererkennung
• Präferenzregression
• Quadratischer Klassifikator
• Statistische Klassifikation

Verweise

Weiterlesen

• Duda, RO; Hart, PE; Storch, DH (2000). Musterklassifizierung (2. Aufl.). Wiley Interscience. ISBN 978-0-471-05669-0. MR  1.802.993 .
• Hilbe, JM (2009). Logistische Regressionsmodelle . Chapman & Hall/CRC-Presse. ISBN 978-1-4200-7575-5.
• Mika, S.; et al. (1999). „Fisher Diskriminanzanalyse mit Kernels“. Neuronale Netze für die Signalverarbeitung IX: Proceedings of the 1999 IEEE Signal Processing Society Workshop (Kat.-Nr. 98TH8468) . IEEE Conference on Neuronal Networks for Signal Processing IX . S. 41–48. CiteSeerX  10.1.1.35.9904 . doi : 10.1109/NNSP.1999.788121 . ISBN 978-0-7803-5673-3. S2CID  8473401 .
• McFarland, H.Richard; Donald, St. P. Richards (2001). "Exakte Fehlklassifizierungswahrscheinlichkeiten für Plug-In-normale quadratische Diskriminanzfunktionen. I. Der Fall mit gleichen Mittelwerten" . Zeitschrift für multivariate Analyse . 77 (1): 21–53. doi : 10.1006/jmva.2000.1924 .
• McFarland, H.Richard; Donald, St. P. Richards (2002). "Exakte Fehlklassifikationswahrscheinlichkeiten für Plug-In-normale quadratische Diskriminanzfunktionen. II. Der heterogene Fall" . Zeitschrift für multivariate Analyse . 82 (2): 299–330. doi : 10.1006/jmva.2001.2034 .
• Haghighat, M.; Abdel-Mottaleb, M.; Alhalabi, W. (2016). "Discriminant Correlation Analysis: Real-Time Feature Level Fusion für multimodale biometrische Erkennung" . IEEE-Transaktionen zu Informationsforensik und -sicherheit . 11 (9): 1984–1996. doi : 10.1109/TIFS.2016.2569061 . S2CID  15624506 .

Externe Links

• Diskriminante Korrelationsanalyse (DCA) des Haghighat-Artikels (siehe oben)
• ALGLIB enthält eine Open-Source-LDA-Implementierung in C# / C++ / Pascal / VBA.
• LDA in Python - LDA-Implementierung in Python
• LDA-Tutorial mit MS Excel
• Biomedizinische Statistik. Diskriminanzanalyse
• StatQuest: Linear Discriminant Analysis (LDA) auf YouTube anschaulich erklärt
• Kursnotizen, Diskriminanzfunktionsanalyse von G. David Garson, NC State University
• Diskriminanzanalyse-Tutorial in Microsoft Excel von Kardi Teknomo
• Kursnotizen, Diskriminanzfunktionsanalyse von David W. Stockburger, Missouri State University
• Diskriminanzfunktionsanalyse (DA) von John Poulsen und Aaron French, San Francisco State University