Metallischer Mittelwert - Metallic mean

Goldener Schnitt im Pentagramm und Silberschnitt im Achteck.

Die metallischen Mittel (auch Verhältnisse oder Konstanten ) der aufeinanderfolgenden natürlichen Zahlen sind die Kettenbrüche :

${\displaystyle n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+\ddots \,}}}}}}}}=[ n;n,n,n,n,\dots]={\frac {n+{\sqrt {n^{2}+4}}}{2}}.}$

Der Goldene Schnitt (1,618...) ist der metallische Mittelwert zwischen 1 und 2, während der Silberanteil (2.414...) der metallische Mittelwert zwischen 2 und 3 ist. Der Begriff "Bronze-Verhältnis" (3,303...) oder Begriffe, die andere Namen von Metallen verwenden (wie Kupfer oder Nickel), werden gelegentlich verwendet, um nachfolgende metallische Mittel zu benennen. Die Werte der ersten zehn metallischen Mittelwerte sind rechts dargestellt. Beachten Sie, dass jeder metallische Mittelwert eine Wurzel der einfachen quadratischen Gleichung ist: , wobei eine beliebige positive natürliche Zahl ist. ${\displaystyle x^{2}-nx=1}$${\displaystyle n}$

Da der Goldene Schnitt mit dem Fünfeck (erste Diagonale/Seite) verbunden ist, ist der Silberschnitt mit dem Achteck (zweite Diagonale/Seite) verbunden. Da das Goldene Verhältnis mit den Fibonacci-Zahlen verbunden ist , ist das Silber-Verhältnis mit den Pell-Zahlen verbunden und das Bronze-Verhältnis ist mit OEIS :  A006190 verbunden . Jede Fibonacci-Zahl ist die Summe der vorherigen Zahl mal eins plus die Zahl davor, jede Pell-Zahl ist die Summe der vorherigen Zahl mal zwei und die davor, und jede "bronze Fibonacci-Zahl" ist die Summe der vorherigen Zahl mal drei plus die Zahl davor. Nimmt man aufeinanderfolgende Fibonacci-Zahlen als Verhältnisse, nähern sich diese Verhältnisse dem goldenen Mittel, die Verhältnisse der Pell-Zahl nähern sich dem silbernen Mittel und die Verhältnisse der "bronzenen Fibonacci-Zahl" nähern sich dem bronzenen Mittel.

Eigenschaften

Entfernt man am Ende eines goldenen Rechtecks ​​das größtmögliche Quadrat, bleibt ein goldenes Rechteck übrig. Wenn man zwei von einem Silber entfernt, bleibt einem ein Silber übrig. Wenn man drei von einer Bronze entfernt, bleibt man mit einer Bronze übrig. Untersuchen Sie die gestrichelten Linien, die die Grenzen der perfekten Quadrate innerhalb jedes Rechtecks ​​darstellen, und beachten Sie, dass die Anzahl dieser gestrichelten Linien immer gleich N ist.

Gold-, Silber- und Bronze-Verhältnisse innerhalb ihrer jeweiligen Rechtecke.

Diese Eigenschaften gelten nur für ganze Zahlen m . Für Nicht-Ganzzahlen sind die Eigenschaften ähnlich, aber etwas anders.

Die obige Eigenschaft für die Potenzen des Silberverhältnisses ist eine Folge einer Eigenschaft der Potenzen der Silbermittel. Für den Silbermittelwert S von m kann die Eigenschaft verallgemeinert werden als

${\displaystyle S_{m}^{n}=K_{n}S_{m}+K_{(n-1)}}$

wo

${\displaystyle K_{n}=mK_{(n-1)}+K_{(n-2)}.}$

Unter Verwendung der Anfangsbedingungen K ₀ = 1 und K ₁ = m wird diese Rekursionsbeziehung zu

${\displaystyle K_{n}={\frac {S_{m}^{n+1}-{\left(m-S_{m}\right)}^{n+1}}{\sqrt {m^ {2}+4}}}.}$

Die Kräfte des Silbermittels haben weitere interessante Eigenschaften:

Wenn n eine positive gerade ganze Zahl ist:

${\displaystyle {S_{m}^{n}-\left\lfloor S_{m}^{n}\right\rfloor}=1-S_{m}^{-n}.}$

Zusätzlich,

${\displaystyle {1 \over {S_{m}^{4}-\left\lfloor S_{m}^{4}\right\rfloor}}+\left\lfloor S_{m}^{4}-1 \right\rfloor =S_{\left(m^{4}+4m^{2}+1\right)}}$

${\displaystyle {1 \over {S_{m}^{6}-\left\lfloor S_{m}^{6}\right\rfloor}}+\left\lfloor S_{m}^{6}-1 \right\rfloor =S_{\left(m^{6}+6m^{4}+9m^{2}+1\right)}.}$

Ein goldenes Dreieck. Das Verhältnis a:b entspricht dem Goldenen Schnitt φ. In einem silbernen Dreieck wäre dies äquivalent zu δ _S .

Ebenfalls,

${\displaystyle S_{m}^{3}=S_{\left(m^{3}+3m\right)}}$

${\displaystyle S_{m}^{5}=S_{\left(m^{5}+5m^{3}+5m\right)}}$

${\displaystyle S_{m}^{7}=S_{\left(m^{7}+7m^{5}+14m^{3}+7m\right)}}$

${\displaystyle S_{m}^{9}=S_{\left(m^{9}+9m^{7}+27m^{5}+30m^{3}+9m\right)}}$

${\displaystyle S_{m}^{11}=S_{\left(m^{11}+11m^{9}+44m^{7}+77m^{5}+55m^{3}+11m\right )}.}$

Im Allgemeinen:

${\displaystyle S_{m}^{2n+1}=S_{\sum _{k=0}^{n}{{2n+1} \over {2k+1}}{{n+k} \choose {2k}}m^{2k+1}}.}$

Der Silbermittelwert S von m hat auch die Eigenschaft, dass

${\displaystyle {\frac {1}{S_{m}}}=S_{m}-m}$

Dies bedeutet, dass der Kehrwert eines Silbermittels denselben Dezimalteil wie der entsprechende Silbermittelwert hat.

${\displaystyle S_{m}=a+b}$

wobei a der ganzzahlige Teil von S und b der Dezimalteil von S ist , dann ist die folgende Eigenschaft wahr:

${\displaystyle S_{m}^{2}=a^{2}+mb+1.}$

Denn (für alle m größer als 0) ist der ganzzahlige Teil von S _m = m , a = m . Für m > 1 gilt dann

${\displaystyle S_{m}^{2}=ma+mb+1}$

${\displaystyle S_{m}^{2}=m(a+b)+1}$

${\displaystyle S_{m}^{2}=m\left(S_{m}\right)+1.}$

Daher ist der Silbermittelwert von m eine Lösung der Gleichung

${\displaystyle x^{2}-mx-1=0.}$

Es kann auch nützlich sein zu beachten, dass der Silbermittelwert S von − m die Umkehrung des Silbermittelwerts S von m . ist

${\displaystyle {\frac {1}{S_{m}}}=S_{(-m)}=S_{m}-m.}$

Ein weiteres interessantes Ergebnis kann durch eine geringfügige Änderung der Formel des Silbermittelwerts erhalten werden. Wenn wir eine Zahl betrachten

${\displaystyle {\frac {n+{\sqrt {n^{2}+4c}}}{2}}=R}$

dann sind die folgenden Eigenschaften wahr:

${\displaystyle R-\lfloor R\rfloor ={\frac {c}{R}}}$wenn c reell ist,

${\displaystyle \left({1 \over R}\right)c=R-\lfloor \operatorname {Re} (R)\rfloor }$wenn c ein Vielfaches von i ist .

Der Silbermittelwert von m ergibt sich auch aus dem Integral

${\displaystyle S_{m}=\int _{0}^{m}{\left({x \over {2{\sqrt {x^{2}+4}}}}+{{m+2} \over {2m}}\right)}\,dx.}$

Eine weitere interessante Form des metallischen Mittelwerts ist gegeben durch

${\displaystyle {\frac {n+{\sqrt {n^{2}+4}}}{2}}=e^{\operatorname {arsinh(n/2)} }}$

Trigonometrische Ausdrücke

n	Trigonometrischer Ausdruck	Zugehöriges regelmäßiges Vieleck
1	${\displaystyle 2\cos {\frac {\pi }{5}}}$	Pentagon
2	${\displaystyle \tan {\frac {3\pi }{8}}}$	Achteck
3	${\displaystyle 8\cos {\frac {\pi }{13}}\cos {\frac {3\pi }{13}}\cos {\frac {4\pi }{13}}}$	Dreizehneck
4	${\displaystyle 8\cos ^{3}{\frac {\pi }{5}}}$	Pentagon
5	${\displaystyle 128\cos {\frac {\pi }{29}}\cos {\frac {4\pi }{29}}\cos {\frac {5\pi }{29}}\cos {\frac {6\pi }{29}}\cos {\frac {7\pi }{29}}\cos {\frac {9\pi }{29}}\cos {\frac {13\pi }{29} }}$	29-gon
6	${\displaystyle {\frac {\sin {\frac {21\pi }{40}}}{\sin {\frac {7\pi }{8}}-\sin {\frac {5\pi }{8 }}\sin {\frac {\pi }{40}}\csc {\frac {11\pi }{40}}-\sin {\frac {19\pi }{20}}\sin {\frac { 9\pi }{40}}\csc {\frac {7\pi }{10}}}}}$	40-gon
7
8	${\displaystyle {\frac {\sin {\frac {6\pi }{17}}\sin {\frac {7\pi }{17}}\sin {\frac {3\pi }{17}}\ sin {\frac {12\pi }{17}}}{\sin {\frac {\pi }{17}}\sin {\frac {9\pi }{17}}\sin {\frac {4\ pi }{17}}\sin {\frac {2\pi }{17}}}}}$	Siebenzehneck
9

Geometrische Konstruktion

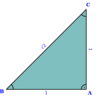
Der metallische Mittelwert für jede gegebene ganze Zahl kann auf folgende Weise geometrisch konstruiert werden. Definiert ein rechtwinkliges Dreieck mit Seiten und mit Längen von , und ist. Das th metallische Mittel ist einfach die Summe der Länge von und der Hypotenuse , . ${\displaystyle N}$${\displaystyle A}$${\displaystyle B}$${\displaystyle 1}$${\displaystyle N/2}$${\displaystyle N}$${\displaystyle M}$${\displaystyle B}$${\displaystyle H}$

Für , ${\displaystyle N=1}$

N = 1

${\displaystyle H={\sqrt {(N/2)^{2}+1^{2}}}={\sqrt {5/4}}=1.1180339...}$

und so

${\displaystyle M=B+H=1/2+1.1180339...=1.6180339...=}$ .

Die Einstellung ergibt den Silberanteil . ${\displaystyle N=2}$

N = 2

${\displaystyle H={\sqrt {(2/2)^{2}+1^{2}}}={\sqrt {2}}=1,4142135...}$

Daher

${\displaystyle M=B+H=2/2+1.4142135...=2.4142135...}$

Ebenso würde das Bronzeverhältnis mit so . berechnet${\displaystyle N=3}$

N = 3

${\displaystyle H={\sqrt {(3/2)^{2}+1^{2}}}={\sqrt {13/4}}=1,8027756...}$

ergibt

${\displaystyle M=B+H=3/2+1.8027756...=3.3027756...}$

Nicht ganzzahlige Argumente erzeugen manchmal Dreiecke mit einem Mittelwert, der selbst eine ganze Zahl ist. Beispiele sind N = 1,5, wobei

N = 1,5

${\displaystyle H={\sqrt {(1.5/2)^{2}+1^{2}}}={\sqrt {1.5625}}=1.25}$

und

${\displaystyle M=B+H=1,5/2+1,25=2}$

Das ist einfach eine verkleinerte Version des 3-4-5 pythagoräischen Dreiecks .

Siehe auch

• Konstante
• Bedeuten
• Verhältnis
• Plastiknummer

Anmerkungen

Verweise

Weiterlesen

• Stakhov, Alekseĭ Petrovich (2009). Die Mathematik der Harmonie: Von Euklid zur zeitgenössischen Mathematik und Informatik , S. 228, 231. World Scientific. ISBN  9789812775832 .

Externe Links

• Cristina-Elena Hrețcanu und Mircea Crasmareanu (2013). " Metallische Strukturen auf Riemannschen Mannigfaltigkeiten ", Revista de la Unión Matemática Argentinien .
• Rakočević, Miloje M. " Weitere Verallgemeinerung des Goldenen Mittelwerts in Bezug auf die 'göttliche' Gleichung von Euler ", Arxiv.org .