Modulares Gitter - Modular lattice

Ein modulares Gitter der Ordnungsdimension 2. Wie bei allen endlichen 2-dimensionalen Gittern ist sein Hasse-Diagramm ein st- planarer Graph .

Im Zweig der Mathematik bezeichnet , um Theorie , ein modulares Gitters ist ein Gitter , dass erfüllt die folgende Selbst dual Bedingung,

Modulares Recht: $a \leq b$ impliziert $a \lor (x \land b) = (a \lor x) \land b$

wobei $x, a, b$ beliebige Elemente im Gitter sind, ≤ die Teilordnung ist und ∨ und ∧ (jeweils Join und Meet genannt ) die Operationen des Gitters sind. Diese Formulierung betont eine Interpretation im Sinne einer Projektion auf das Untergitter $[a, b]$ , eine Tatsache, die als Diamantisomorphiesatz bekannt ist . Eine alternative, aber äquivalente Bedingung in Form einer Gleichung (siehe unten) betont, dass modulare Gitter eine Varietät im Sinne der universellen Algebra bilden .

Modulare Gitter entstehen natürlich in der Algebra und in vielen anderen Bereichen der Mathematik. In diesen Szenarien Modularität ist eine Abstraktion des 2 ^nd Isomorphiesatz . Zum Beispiel bilden die Unterräume eines Vektorraums (und allgemeiner die Untermodule eines Moduls über einem Ring ) ein modulares Gitter.

In einem nicht unbedingt modularen Gitter kann es noch Elemente $b geben,$ für die das Modulgesetz in Verbindung mit beliebigen Elementen $x$ und $a$ (für $a \leq b$ ) gilt. Ein solches Element wird als modulares Element bezeichnet . Noch allgemeiner kann das modulare Gesetz für jedes $a$ und ein festes Paar $(x, b) gelten$ . Ein solches Paar wird als modulares Paar bezeichnet , und es gibt verschiedene Verallgemeinerungen der Modularität, die sich auf diesen Begriff und auf die Semimodularität beziehen .

Modulare Gitter werden manchmal Dedekind-Gitter genannt, nach Richard Dedekind , der die modulare Identität in mehreren motivierenden Beispielen entdeckte .

Einführung

Das modulare Gesetz kann als eingeschränktes Assoziativgesetz betrachtet werden , das die beiden Gitteroperationen ähnlich wie das Assoziativgesetz λ(μ x ) = (λμ) x für Vektorräume Multiplikation im Körper und Skalarmultiplikation verbindet.

Die Beschränkung $a \leq b$ ist eindeutig erforderlich, da es aus folgt $einem \lor (x \land b) = (a \lor x) \land b$ . Mit anderen Worten, kein Gitter mit mehr als einem Element erfüllt die uneingeschränkte Konsequenz des Modulgesetzes.

Es ist leicht zu sehen , dass $ein \leq b$ impliziert $eine \lor (x \land b) \leq (a \lor x) \land b$ in jedem Gitter. Daher kann das modulare Gesetz auch formuliert werden als

Modulares Gesetz (Variante): $a \leq b$ bedeutet $, (a \lor x) \land b \leq a \lor (x \land b)$ .

Das modulare Gesetz kann als Gleichung ausgedrückt werden, die unbedingt gelten muss. Da $a \leq b$ impliziert $a = a \land b$ und da $a \land b \leq b$ , ersetze $a$ durch $a \land b$ in der Definitionsgleichung des modularen Gesetzes, um zu erhalten:

Modulare Identität: $(A \land b) \lor (x \land b) = ((a \land b) \lor x) \land b$ .

Dies zeigt, dass die modularen Gitter unter Verwendung der Terminologie der universellen Algebra eine Untervarietät der Vielfalt der Gitter bilden. Daher sind alle homomorphen Bilder, Untergitter und direkten Produkte modularer Gitter wieder modular.

Beispiele

N ₅ , das kleinste nichtmodulare Gitter: x ∨( a ∧ b ) = x ∨0 = x ≠ b = 1∧ b = ( x ∨ a )∧ b .

Das Gitter von Submodulen eines Moduls über einem Ring ist modular. Als Sonderfall ist das Untergruppengitter einer abelschen Gruppe modular.

Das Gitter der normalen Untergruppen einer Gruppe ist modular. Aber im Allgemeinen ist das Gitter aller Untergruppen einer Gruppe nicht modular. Zum Beispiel ist das Gitter von Untergruppen der Diedergruppe der Ordnung 8 nicht modular.

Das kleinste nichtmodulare Gitter ist das "Pentagon"-Gitter N ₅ bestehend aus fünf Elementen 0, 1, x , a , b mit 0 < x < b < 1, 0 < a < 1, und a ist nicht mit x . vergleichbar oder zu b . Für dieses Gitter

x ∨ ( a ∧ b ) = x ∨ 0 = x < b = 1 ∧ b = ( x ∨ a ) ∧ b

gilt im Widerspruch zum Modulgesetz. Jedes nichtmodulare Gitter enthält eine Kopie von N ₅ als Untergitter.

Eigenschaften

Jedes Verteilungsgitter ist modular.

Dilworth (1954) bewies, dass in jedem endlichen modularen Gitter die Anzahl der verbindenden irreduziblen Elemente gleich der Anzahl der treffen-irreduziblen Elemente ist. Allgemeiner gesagt , für jedes $k$ ist die Anzahl der Elemente des Gitters, die genau $k$ andere Elemente überdecken, gleich der Anzahl, die von genau $k$ anderen Elementen überdeckt werden .

Eine nützliche Eigenschaft, um zu zeigen, dass ein Gitter nicht modular ist, ist wie folgt:

Ein Gitter

G

ist genau dann modular, wenn für jedes

a, b, c \in G

,

{\Big (}(c\leq a){\text{ und }}(a\wedge b=c\wedge b){\text{ und }}(a\vee b=c\vee b) {\Groß)}\Rechtspfeil (a=c)

Beweisskizze: Sei G modular und die Prämisse der Implikation gelte. Dann mit Absorption und modularer Identität:

c = ( c ∧ b ) c = ( a ∧ b ) ∨ c = a ∧ ( b ∨ c ) = a ∧ ( b ∨ a ) = a

Für die andere Richtung gelte die Implikation des Satzes in G. Seien a , b , c beliebige Elemente in G, so dass c ≤ a . Let x = ( a ∧ b ) ∨ c , y = eine ∧ ( B ∨ C ). Aus der modularen Ungleichung folgt sofort x ≤ y . Wenn wir diese zeigen x ∧ b = y ∧ b , x ∨ b = y ∨ b , dann mit der Annahme x = y muss halten. Der Rest des Beweises ist routinemäßige Manipulation mit Infima, Suprema und Ungleichungen.

Satz des Diamantisomorphismus

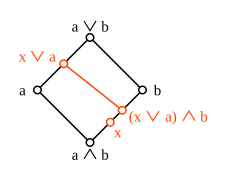
Für zwei beliebige Elemente a , b eines modularen Gitter kann man die Intervalle betrachten [ a ∧ b , b ] und [ a , a ∨ b ]. Sie sind durch ordnungserhaltende Karten verbunden

φ: [ a ∧ b , b ] → [ a , a ∨ b ] und

: [ a , a ∨ b ] → [ a ∧ b , b ]

die definiert sind durch φ( x ) = x ∨ a und ψ( y ) = y ∧ b .

In einem modularen Gitter sind die durch die Pfeile gekennzeichneten Abbildungen φ und ψ gegenseitig inverse Isomorphismen.
Versagen des Diamantisomorphismussatzes in einem nichtmodularen Gitter.

Die Zusammensetzung ψφ ist eine ordnungserhaltende Abbildung vom Intervall [ a ∧ b , b ] auf sich selbst, die auch die Ungleichung ψ(φ( x )) = ( x ∨ a ) ∧ b ≥ x erfüllt . Das Beispiel zeigt, dass diese Ungleichung im Allgemeinen streng sein kann. In einem modularen Gitter gilt jedoch Gleichheit. Da das Dual eines modularen Gitters wiederum modular ist, ist φψ auch die Identität auf [ a , a ∨ b ], und daher sind die beiden Abbildungen φ und ψ Isomorphismen zwischen diesen beiden Intervallen. Dieses Ergebnis wird manchmal als Diamantisomorphismussatz für modulare Gitter bezeichnet. Ein Gitter ist genau dann modular, wenn der Satz der Diamantisomorphie für jedes Elementpaar gilt.

Der Diamant-Isomorphismussatz für modulare Gitter ist analog zum zweiten Isomorphismussatz in der Algebra und eine Verallgemeinerung des Gittersatzes .

Modulare Paare und verwandte Begriffe

Das zentrierte Sechseckgitter S ₇ , auch als D _{2 bekannt} , ist M-symmetrisch, aber nicht modular.

In jedem Gitter, ein modulares Paar ist ein Paar ( a, b ) von Elementen , so dass für alle x erfüllt a ∧ b ≤ x ≤ b , haben wir ( x ∨ a ) ∧ b = x , das heißt , wenn eine Hälfte des Diamanten Der Isomorphismussatz gilt für das Paar. Ein Element b eines Gitters heißt (rechtes) modulares Element, wenn ( a, b ) ein modulares Paar für alle Elemente a ist .

Ein Gitter mit der Eigenschaft, dass wenn ( a, b ) ein modulares Paar ist, dann ist ( b, a ) auch ein modulares Paar, wird als M-symmetrisches Gitter bezeichnet . Da ein Gitter genau dann modular ist, wenn alle Paare von Elementen modular sind, ist offensichtlich jedes modulare Gitter M-symmetrisch. In dem oben beschriebenen Gitter N ₅ ist das Paar ( b, a ) modular, das Paar ( a, b ) jedoch nicht. Daher ist N ₅ nicht M-symmetrisch. Das zentrierte Sechseckgitter S ₇ ist M-symmetrisch aber nicht modular. Da N ₅ ein Untergitter von S _{7 ist} , folgt daraus, dass die M-symmetrischen Gitter keine Untervarietät der Vielfalt von Gittern bilden.

M-Symmetrie ist kein selbstdualer Begriff. Ein duales modulares Paar ist ein Paar, das im dualen Gitter modular ist , und ein Gitter wird dual M-symmetrisch oder M ^* -symmetrisch genannt, wenn sein Dual M-symmetrisch ist. Es kann gezeigt werden, dass ein endliches Gitter genau dann modular ist, wenn es M-symmetrisch und M ^* -symmetrisch ist. Die gleiche Äquivalenz gilt für unendliche Gitter, die die aufsteigende Kettenbedingung (oder die absteigende Kettenbedingung) erfüllen.

Einige weniger wichtige Begriffe sind ebenfalls eng miteinander verbunden. Ein Gitter ist kreuzsymmetrisch, wenn für jedes modulare Paar ( a, b ) das Paar ( b, a ) dualmodular ist. Kreuzsymmetrie impliziert M-Symmetrie, aber nicht M ^* -Symmetrie. Daher ist Kreuzsymmetrie nicht gleichbedeutend mit dualer Kreuzsymmetrie. Ein Gitter mit dem kleinsten Element 0 ist ⊥-symmetrisch, wenn für jedes modulare Paar ( a, b ), das a ∧ b = 0 erfüllt, auch das Paar ( b, a ) modular ist.

Geschichte

Freies modulares Gitter erzeugt durch drei Elemente {x,y,z}

Die Definition der Modularität geht auf Richard Dedekind zurück , der nach seiner Pensionierung die meisten einschlägigen Arbeiten veröffentlichte. In einem Papier im Jahr 1894 veröffentlicht studierte er Gittern, die er als Dual - Gruppen ( deutsch : Dualgruppen ) als Teil seiner „Algebra der Module “ und festgestellt , dass Ideale erfüllen , was wir heute als das modulare Gesetz. Er beobachtete auch, dass für Gitter im Allgemeinen das modulare Gesetz seinem dualen Gesetz entspricht.

In einer anderen Arbeit aus dem Jahr 1897 untersuchte Dedekind das Gitter von Teilern mit gcd und lcm als Operationen, so dass die Gitterordnung durch die Teilbarkeit gegeben ist. In einem Exkurs führte er Gitter in einen allgemeinen Kontext ein und untersuchte sie formal. Er beobachtete, dass das Gitter der Untermodule eines Moduls der modularen Identität genügt. Er nannte solche Gitter Dual Gruppen von Modultyp ( Dualgruppen vom Modultypus ). Er bewies auch, dass die modulare Identität und ihr Duales gleichwertig sind.

In derselben Arbeit untersuchte Dedekind auch die folgende stärkere Form der modularen Identität, die ebenfalls selbstdual ist:

( X ∧ b ) ∨ ( a ∧ b ) = [ x ∨ a ] ∧ b .

Er nannte Gitter, die dieser Identität genügen, duale Gruppen vom Idealtypus ( Dualgruppen vom Idealtypus ). In der modernen Literatur werden sie häufiger als Verteilungsgitter bezeichnet . Er gab Beispiele für ein nicht modulares Gitter und für ein modulares Gitter, das nicht idealtypisch ist.

Ein 1900 von Dedekind veröffentlichter Aufsatz hatte Gitter als zentrales Thema: Er beschrieb das aus drei Elementen erzeugte freie modulare Gitter, ein Gitter mit 28 Elementen (siehe Bild).

Siehe auch

Modularer Graph , eine Klasse von Graphen, die die Hasse-Diagramme von modularen Gittern enthält
Young-Fibonacci-Gitter , ein unendliches modulares Gitter, das auf Zeichenfolgen der Ziffern 1 und 2 definiert ist
Orthomodulares Gitter
Iwasawa-Gruppe

Anmerkungen

^ "Warum sind modulare Gitter wichtig?" . Stack-Austausch für Mathematik . Abgerufen 2018-09-17 .
^ Das Folgende ist für jedes Gitter true: $a \lor (x \land b) \leq (a \lor x) \land (a \lor b)$ . Auchwenn $a \leq b$ , dann $a \lor b = b$ .
^ Blyth, TS (2005). "Modulare Gitter" . Gitter und geordnete algebraische Strukturen . Universitätsex. London: Springer. Satz 4.4. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0.
^ Blyth, TS (2005). "Modulare Gitter" . Gitter und geordnete algebraische Strukturen . Universitätsex. London: Springer. P. 65. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0.
^ In einem Verteilungsgitter gilt:. Darüber hinaus gilt das Absorptionsgesetz,, für jedes Gitter. Setzt man dies für die zweite Konjunktion der rechten Seite der ersten Gleichung ein, erhält man die Modulare Identität. $(a\keil b)\vee (x\keil b)=((a\keil b)\vee x)\keil ((a\keil b)\vee b)$ $(a\wedge b)\vee b=b$
^ Dilworth, RP (1954), "Beweis einer Vermutung über endliche modulare Gitter", Annals of Mathematics , Second Series, 60 (2): 359–364, doi : 10.2307/1969639 , JSTOR 1969639 , MR 0063348. Nachgedruckt in Bogart, Kenneth P.; Freese, Ralph; Kung, Joseph PS, Hrsg. (1990), "Proof of a Conjecture on Finite Modular Lattices", The Dilworth Theorems: Selected Papers of Robert P. Dilworth , Contemporary Mathematicians, Boston: Birkhäuser, S. 219–224, doi : 10.1007/978-1-4899- 3558-8_21 , ISBN 978-1-4899-3560-1
^ Der französische Begriff für modulares Paar ist pair modulaire . Ein Paar ( a, b ) heißtim Französischen paire modulaire, wenn sowohl ( a, b ) als auch ( b, a ) modulare Paare sind.
^ Einige Autoren, zB Fofanova (2001), bezeichnen solche Gitter als semimodulare Gitter . Da jedes M-symmetrische Gitter semimodular ist und für Gitter endlicher Länge das Umgekehrte gilt, kann dies nur bei unendlichen Gittern zu Verwirrung führen.
^ ^a ^b ^c ^d ^e ^f ^g Dedekind, Richard (1897), "Über Zerlegungen von Zahlen durch ihre grössten gemeinsamen Theiler" (PDF) , Festschrift der Herzogl. Technischen Hochschule Carolo-Wilhelmina bei Gelegenheit der 69. Versammlung Deutscher Naturforscher und Ärzte in Braunschweig , Friedrich Vieweg und Sohn
^ Dedekind, Richard (1900), "Über die von drei Moduln erzeugte Dualgruppe" , Mathematische Annalen , 53 (3): 371–403, doi : 10.1007/BF01448979

Verweise

Corry, Leo (2003-11-27), Moderne Algebra und der Aufstieg mathematischer Strukturen (2. Aufl.), S. 121–129, ISBN 978-3-7643-7002-2
Fofanova, T. S. (2001) [1994], "Semi-modular lattice" , Encyclopedia of Mathematics , EMS Press
Maeda, Shûichirô (1965), „Über die Symmetrie der modularen Beziehung in Atomgittern“ , Journal of Science der Hiroshima University , 29 : 165–170
Rota, Gian-Carlo (1997), "Die vielen Leben der Gittertheorie" (PDF) , Mitteilungen der American Mathematical Society , 44 (11): 1440–1445, ISSN 0002-9920
Skornyakov, L. A. (2001) [1994], "Modulares Gitter" , Encyclopedia of Mathematics , EMS Press
Stern, Manfred (1999), Semimodulare Gitter , Cambridge University Press , ISBN 978-0-521-46105-4

Externe Links

"Modulares Gitter" . PlanetMath .
OEIS- Sequenz A006981 (Anzahl der unbeschrifteten modularen Gitter mit n Elementen)
Free Modular Lattice Generator Eine browserbasierte Open-Source-Webanwendung, die einige kostenlose modulare Gitter erzeugen und visualisieren kann.

[1] "Warum sind modulare Gitter wichtig?" . Stack-Austausch für Mathematik . Abgerufen 2018-09-17 .

[2] Das Folgende ist für jedes Gitter true: $a \lor (x \land b) \leq (a \lor x) \land (a \lor b)$ . Auchwenn $a \leq b$ , dann $a \lor b = b$ .

[:0-3] Blyth, TS (2005). "Modulare Gitter" . Gitter und geordnete algebraische Strukturen . Universitätsex. London: Springer. Satz 4.4. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0.

[4] Blyth, TS (2005). "Modulare Gitter" . Gitter und geordnete algebraische Strukturen . Universitätsex. London: Springer. P. 65. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0.

[5] In einem Verteilungsgitter gilt:. Darüber hinaus gilt das Absorptionsgesetz,, für jedes Gitter. Setzt man dies für die zweite Konjunktion der rechten Seite der ersten Gleichung ein, erhält man die Modulare Identität. $(a\keil b)\vee (x\keil b)=((a\keil b)\vee x)\keil ((a\keil b)\vee b)$ $(a\wedge b)\vee b=b$

[6] Dilworth, RP (1954), "Beweis einer Vermutung über endliche modulare Gitter", Annals of Mathematics , Second Series, 60 (2): 359–364, doi : 10.2307/1969639 , JSTOR 1969639 , MR 0063348. Nachgedruckt in Bogart, Kenneth P.; Freese, Ralph; Kung, Joseph PS, Hrsg. (1990), "Proof of a Conjecture on Finite Modular Lattices", The Dilworth Theorems: Selected Papers of Robert P. Dilworth , Contemporary Mathematicians, Boston: Birkhäuser, S. 219–224, doi : 10.1007/978-1-4899- 3558-8_21 , ISBN 978-1-4899-3560-1

[7] Der französische Begriff für modulares Paar ist pair modulaire . Ein Paar ( a, b ) heißtim Französischen paire modulaire, wenn sowohl ( a, b ) als auch ( b, a ) modulare Paare sind.

[8] Einige Autoren, zB Fofanova (2001), bezeichnen solche Gitter als semimodulare Gitter . Da jedes M-symmetrische Gitter semimodular ist und für Gitter endlicher Länge das Umgekehrte gilt, kann dies nur bei unendlichen Gittern zu Verwirrung führen.

[Dedekind.1897-9] ^ ^a ^b ^c ^d ^e ^f ^g Dedekind, Richard (1897), "Über Zerlegungen von Zahlen durch ihre grössten gemeinsamen Theiler" (PDF) , Festschrift der Herzogl. Technischen Hochschule Carolo-Wilhelmina bei Gelegenheit der 69. Versammlung Deutscher Naturforscher und Ärzte in Braunschweig , Friedrich Vieweg und Sohn

[10] Dedekind, Richard (1900), "Über die von drei Moduln erzeugte Dualgruppe" , Mathematische Annalen , 53 (3): 371–403, doi : 10.1007/BF01448979

Languages

In other projects