Monty Hall-Problem - Monty Hall problem
Das Monty-Hall-Problem ist eine Denksportaufgabe in Form eines Wahrscheinlichkeitsrätsels , die lose auf der amerikanischen Fernsehspielshow Let's Make a Deal basiert und nach ihrem ursprünglichen Gastgeber Monty Hall benannt ist . Das Problem wurde ursprünglich in einem Brief von Steve Selvin an den amerikanischen Statistiker im Jahr 1975 gestellt (und gelöst). Berühmt wurde es durch eine Frage des Lesers Craig F. Whitakers Brief, der in Marilyn vos Savant in der Kolumne „Ask Marilyn“ im Parade- Magazin zitiert wird in 1990:
Angenommen, Sie sind in einer Spielshow und haben die Wahl zwischen drei Türen: Hinter einer Tür befindet sich ein Auto; hinter den anderen Ziegen. Sie wählen eine Tür, sagen wir Nr. 1, und der Gastgeber, der weiß, was sich hinter den Türen befindet, öffnet eine andere Tür, sagen wir Nr. 3, die eine Ziege hat. Dann sagt er zu dir: "Möchtest du Tür Nr. 2 wählen?" Ist es zu Ihrem Vorteil, Ihre Wahl zu ändern?
Vos Savants Antwort war, dass der Kandidat zur anderen Tür wechseln sollte. Unter den Standardannahmen hat die Schaltstrategie a2/3 Wahrscheinlichkeit , das Auto zu gewinnen, während die Strategie, die bei der ursprünglichen Wahl verbleibt, nur a1/3 Wahrscheinlichkeit.
Wenn der Spieler zum ersten Mal seine Wahl trifft, gibt es ein 2/3Chance, dass sich das Auto hinter einer der nicht gewählten Türen befindet. Diese Wahrscheinlichkeit ändert sich nicht, nachdem der Host eine der nicht gewählten Türen geöffnet hat. Wenn der Gastgeber Informationen über die 2 nicht gewählten Türen gibt (und enthüllt, dass eine von ihnen nicht das Auto dahinter hat), wird die2/3 Die Wahrscheinlichkeit, dass sich das Auto hinter einer der nicht gewählten Türen befindet, beruht auf der nicht gewählten und nicht sichtbaren Tür, im Gegensatz zu der 1/3 Wahrscheinlichkeit, dass das Auto hinter der Tür steht, die der Kandidat ursprünglich gewählt hat.
Die angegebenen Wahrscheinlichkeiten hängen von bestimmten Annahmen darüber ab, wie Gastgeber und Teilnehmer ihre Türen auswählen. Eine wichtige Erkenntnis ist, dass unter diesen Standardbedingungen mehr Informationen über die Türen 2 und 3 vorhanden sind, als zu Beginn des Spiels verfügbar waren, als der Spieler die Tür 1 wählte: Die bewusste Aktion des Gastgebers wertet die Tür auf, die er nicht gewählt hat entscheiden, zu eliminieren, aber nicht zu dem, den der Teilnehmer ursprünglich gewählt hat. Eine weitere Erkenntnis ist, dass das Wechseln von Türen eine andere Aktion ist als die zufällige Auswahl zwischen den beiden verbleibenden Türen, da die erste Aktion die vorherigen Informationen verwendet und die letztere nicht. Andere mögliche Verhaltensweisen des Hosts als das beschriebene können andere oder gar keine zusätzliche Informationen preisgeben und zu anderen Wahrscheinlichkeiten führen.
Viele Leser der Kolumne von vos Savant weigerten sich, zu glauben, dass ein Wechsel von Vorteil ist, und lehnten ihre Erklärung ab. Nachdem das Problem in Parade aufgetaucht war , schrieben ungefähr 10.000 Leser, darunter fast 1.000 mit Doktortiteln , an das Magazin, die meisten von ihnen nannten vos Savant falsch. Selbst wenn Erklärungen, Simulationen und formale mathematische Beweise gegeben wurden, akzeptierten viele Leute immer noch nicht, dass der Wechsel die beste Strategie ist. Paul Erdős , einer der produktivsten Mathematiker der Geschichte, blieb nicht überzeugt, bis ihm eine Computersimulation gezeigt wurde, die das vorhergesagte Ergebnis von vos Savant demonstrierte.
Das Problem ist ein Paradox veridischen Typs, denn die Lösung von Vos Savant ist so kontraintuitiv, dass sie absurd erscheinen kann, aber dennoch nachweislich wahr ist. Das Monty-Hall-Problem ist mathematisch eng mit dem früheren Drei-Gefangenen-Problem und dem viel älteren Bertrand-Box-Paradoxon verwandt .
Paradox
Steve Selvin schrieb 1975 einen Brief an den amerikanischen Statistiker, in dem er ein Problem auf der Grundlage der Spielshow Let's Make a Deal beschrieb und es in einem nachfolgenden Brief als "Monty-Hall-Problem" bezeichnete. Das Problem ist mathematisch äquivalent zu dem Drei-Gefangenen-Problem, das 1959 in Martin Gardners "Mathematical Games"-Kolumne im Scientific American beschrieben wurde, und dem Drei-Schalen-Problem, das in Gardners Buch Aha Gotcha beschrieben ist .
Standardannahmen
Unter den Standardannahmen beträgt die Wahrscheinlichkeit, das Auto nach dem Wechsel zu gewinnen, 2/3. Der Schlüssel zu dieser Lösung ist das Verhalten des Hosts. Mehrdeutigkeiten in der Parade- Version definieren das Protokoll des Hosts nicht explizit. Die neben Whitakers Frage gedruckte Lösung von Marilyn vos Savant impliziert jedoch, und sowohl Selven als auch vos Savant definieren die Rolle des Gastgebers ausdrücklich wie folgt:
- Der Gastgeber muss immer eine Tür öffnen, die nicht vom Teilnehmer ausgewählt wurde.
- Der Gastgeber muss immer eine Tür öffnen, um eine Ziege zu enthüllen und niemals das Auto.
- Der Gastgeber muss immer die Möglichkeit bieten, zwischen der ursprünglich gewählten Tür und der verbleibenden geschlossenen Tür zu wechseln.
Wenn eine dieser Annahmen geändert wird, kann dies die Gewinnwahrscheinlichkeit durch Türwechsel ändern, wie im folgenden Abschnitt beschrieben . Es wird auch typischerweise angenommen, dass das Auto anfangs zufällig hinter den Türen versteckt ist und dass, wenn der Spieler das Auto anfangs auswählt, die Wahl des Gastgebers, welche Ziegenverstecktür zu öffnen ist, zufällig ist. Einige Autoren, unabhängig oder inklusive, gehen davon aus, dass die anfängliche Wahl des Spielers ebenfalls zufällig ist.
Einfache Lösungen
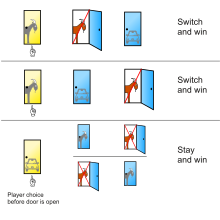
Die von vos Savant in Parade vorgestellte Lösung zeigt die drei möglichen Anordnungen von einem Auto und zwei Ziegen hinter drei Türen und das Ergebnis des Bleibens bzw. Wechselns nach dem anfänglichen Picken von Tür 1 jeweils:
Hinter Tür 1 Hinter Tür 2 Hinter Tür 3 Ergebnis, wenn Sie an Tür Nr. 1 bleiben Ergebnis beim Wechsel auf die angebotene Tür Ziege Ziege Auto Gewinnt Ziege Gewinnt Auto Ziege Auto Ziege Gewinnt Ziege Gewinnt Auto Auto Ziege Ziege Gewinnt Auto Gewinnt Ziege
Ein Spieler, der bei der ursprünglichen Wahl bleibt, gewinnt nur bei einer von drei dieser gleich wahrscheinlichen Möglichkeiten, während ein Spieler, der wechselt, bei zwei von drei gewinnt.
Eine intuitive Erklärung ist , dass, wenn die Teilnehmer zunächst eine Ziege (2 von 3 Türen) aufnimmt, der Teilnehmer wird das Auto durch Umschalten weil die andere Ziege gewinnen kann nicht mehr aufgenommen werden, während , wenn die Teilnehmer zunächst das Auto holen (1 von 3 Türen), der Kandidat wird nicht das Auto durch Umschalten gewinnen. Dass der Gastgeber anschließend eine Ziege in einer der nicht gewählten Türen enthüllt, ändert nichts an der anfänglichen Wahrscheinlichkeit.
Die meisten Leute kommen zu dem Schluss, dass das Wechseln keine Rolle spielt, da es zwei ungeöffnete Türen und ein Auto gibt und es eine 50/50-Wahl ist. Dies wäre der Fall, wenn der Host zufällig eine Tür öffnet, aber das ist nicht der Fall; Die geöffnete Tür hängt von der ursprünglichen Wahl des Spielers ab, daher gilt die Annahme der Unabhängigkeit nicht. Bevor der Gastgeber eine Tür öffnet, gibt es ein1/3Wahrscheinlichkeit, dass sich das Auto hinter jeder Tür befindet. Wenn sich das Auto hinter Tür 1 befindet, kann der Host entweder Tür 2 oder Tür 3 öffnen, daher ist die Wahrscheinlichkeit, dass sich das Auto hinter Tür 1 befindet und der Host Tür 3 öffnet,1/3 × 1/2 = 1/6. Wenn sich das Auto hinter Tür 2 befindet (und der Spieler Tür 1 ausgewählt hat), muss der Host Tür 3 öffnen, daher ist die Wahrscheinlichkeit, dass sich das Auto hinter Tür 2 befindet und der Host Tür 3 öffnet1/3 × 1 = 1/3. Dies sind die einzigen Fälle, in denen der Gastgeber Tür 3 öffnet. Wenn also der Spieler Tür 1 ausgewählt hat und der Gastgeber Tür 3 öffnet, ist die Wahrscheinlichkeit, dass sich das Auto hinter Tür 2 befindet, doppelt so hoch wie bei Tür 1. Der Schlüssel ist, dass, wenn das Auto hinter Tür 2 muss der Gastgeber Tür 3 öffnen, aber wenn sich das Auto hinter Tür 1 befindet, kann der Gastgeber jede Tür öffnen.
Eine andere Möglichkeit, die Lösung zu verstehen, besteht darin, die beiden ursprünglichen, nicht gewählten Türen zusammen zu betrachten. Wie Cecil Adams es ausdrückt: "Monty sagt im Grunde: Sie können Ihre eine Tür behalten oder Sie können die anderen beiden Türen haben." Die2/3Die Chance, das Auto zu finden, hat sich durch das Öffnen einer dieser Türen nicht geändert, da Monty, der den Standort des Autos kennt, mit Sicherheit eine Ziege enthüllt. Die Wahl des Spielers, nachdem der Gastgeber eine Tür geöffnet hat, ist also nicht anders, als wenn der Gastgeber dem Spieler die Option anbietet, von der ursprünglich gewählten Tür zu den beiden verbleibenden Türen zu wechseln . Der Schalter gibt in diesem Fall dem Spieler eindeutig a2/3 Wahrscheinlichkeit, das Auto zu wählen.
Wie Keith Devlin sagt: "Indem Monty seine Tür öffnet, sagt er dem Teilnehmer: 'Es gibt zwei Türen, die Sie nicht gewählt haben, und die Wahrscheinlichkeit, dass sich der Preis hinter einer von ihnen befindet, ist2/3. Ich helfe Ihnen, indem ich mein Wissen nutze, wo sich der Preis befindet, um eine dieser beiden Türen zu öffnen, um Ihnen zu zeigen, dass der Preis nicht verborgen ist. Diese zusätzlichen Informationen können Sie jetzt nutzen. Ihre Wahl von Tür A hat eine Chance von 1 zu 3, der Gewinner zu sein. Ich habe das nicht geändert. Aber durch Tür C beseitigen, habe ich Ihnen gezeigt , dass die Wahrscheinlichkeit , dass Tür B versteckt der Preis ist 2 in 3 ' "
Vos Savant schlägt vor, dass die Lösung mit 1.000.000 Türen intuitiver als mit 3 sein wird. In diesem Fall gibt es 999.999 Türen mit Ziegen dahinter und eine Tür mit einem Preis. Nachdem der Spieler eine Tür ausgewählt hat, öffnet der Host 999.998 der verbleibenden Türen. Im Durchschnitt enthält die verbleibende Tür in 999.999 von 1.000.000 Fällen den Preis. Intuitiv sollte der Spieler fragen, wie wahrscheinlich es ist, dass er bei einer Million Türen anfangs das richtige ausgewählt hat. Stibel et al. schlugen vor, dass die Nachfrage nach dem Arbeitsgedächtnis während des Monty-Hall-Problems besteuert wird und dass dies die Menschen dazu zwingt, ihre Entscheidungen in zwei gleich wahrscheinliche Optionen zu "kollabieren". Sie berichten, dass die Leute dazu neigen, häufiger zu wechseln, wenn die Anzahl der Optionen auf mehr als 7 Optionen (7 Türen) erhöht wird; die meisten Teilnehmer beurteilen die Erfolgswahrscheinlichkeit jedoch immer noch fälschlicherweise bei 50:50.
Vos Savant und die mediale Furore
"Sie haben es vermasselt, und Sie haben es vermasselt! Da Sie anscheinend Schwierigkeiten haben, das Grundprinzip hier zu verstehen, werde ich es erklären. Nachdem der Gastgeber eine Ziege enthüllt hat, haben Sie jetzt eine Chance von eins zu zwei, dass Sie Recht haben." . Ob Sie Ihre Auswahl ändern oder nicht, die Chancen stehen gleich. Es gibt genug mathematische Analphabeten in diesem Land, und wir brauchen nicht den höchsten IQ der Welt, der sich weiter ausbreitet. Schade!“
Scott Smith, Ph.D. Universität von Florida
Vos Savant schrieb in ihrer ersten Kolumne zum Monty-Hall-Problem, dass der Spieler wechseln sollte. Sie erhielt Tausende von Briefen von ihren Lesern – von denen die überwiegende Mehrheit, darunter viele von Lesern mit Doktortitel, mit ihrer Antwort nicht einverstanden war. In den Jahren 1990-1991 waren drei weitere ihrer Kolumnen in Parade dem Paradoxon gewidmet. Zahlreiche Beispiele für Briefe von Lesern der Kolumnen von Vos Savant werden in The Monty Hall Dilemma: A Cognitive Illusion Par Excellence vorgestellt und diskutiert .
Die Diskussion wurde an anderen Orten wiederholt (zB in Cecil Adams ' Zeitungskolumne " The Straight Dope ") und in großen Zeitungen wie der New York Times berichtet .
Um ihre Antwort zu verdeutlichen, schlug sie zur Veranschaulichung ein Hütchenspiel vor: „Du schaust weg, und ich lege eine Erbse unter eine von drei Muscheln. Dann bitte ich dich, deinen Finger auf eine Muschel zu legen eine Erbse sind 1/3, einverstanden? Dann hebe ich einfach eine leere Hülle von den anderen beiden auf. Da ich dies unabhängig von Ihrer Wahl tun kann (und werde), haben wir nichts gelernt, um die Gewinnchancen auf der Schale unter Ihrem Finger zu revidieren." Sie schlug auch eine ähnliche Simulation mit drei Spielkarten vor.
Vos Savant kommentierte , dass, obwohl einige Verwirrung verursacht wurde einige Leser nicht erkennen , dass sie sollten davon ausgehen , dass der Wirt immer eine Ziege offenbaren müssen, die fast alle ihre zahlreichen Korrespondenten hatte richtig verstanden die Problem Annahmen und wurden zunächst noch davon überzeugt , dass vos Savant des Antwort ("switch") war falsch.
Verwirrung und Kritik
Verwirrungsquellen
Beim ersten Mal mit dem Monty-Hall-Problem konfrontiert, geht eine überwältigende Mehrheit der Menschen davon aus, dass jede Tür die gleiche Wahrscheinlichkeit hat und kommt zu dem Schluss, dass das Umschalten keine Rolle spielt. Von 228 Probanden in einer Studie entschieden sich nur 13% für einen Wechsel. In seinem Buch Die Macht des logischen Denkens , Kognitionspsychologe Massimo Piattelli Palmarini schreibt: „Kein anderes statistisches Puzzle kommt so nah an alle die ganze Zeit den Menschen täuschen [und] auch Physiker Nobel systematisch die falsche Antwort geben, und dass sie bestehen darauf, und sie sind bereit, diejenigen, die die richtige Antwort vorschlagen, in gedruckter Form zu beschimpfen." Tauben, die dem Problem immer wieder ausgesetzt sind, zeigen, dass sie im Gegensatz zu Menschen schnell lernen, immer zu wechseln.
Die meisten Aussagen des Problems, insbesondere die in Parade , entsprechen nicht den Regeln der eigentlichen Spielshow und geben das Verhalten des Gastgebers nicht vollständig an oder geben nicht an, dass der Standort des Autos zufällig ausgewählt wird. Krauss und Wang vermuten, dass Menschen die Standardannahmen treffen, auch wenn sie nicht explizit angegeben werden.
Obwohl diese Probleme mathematisch bedeutsam sind, denken fast alle Menschen immer noch, dass jede der beiden ungeöffneten Türen die gleiche Wahrscheinlichkeit hat, und schließen daraus, dass das Umschalten keine Rolle spielt. Diese Annahme der „gleichen Wahrscheinlichkeit“ ist eine tief verwurzelte Intuition. Menschen neigen stark zu der Annahme, dass die Wahrscheinlichkeit gleichmäßig auf so viele Unbekannte verteilt ist, wie vorhanden sind, unabhängig davon, ob dies der Fall ist oder nicht.
Das Problem zieht weiterhin die Aufmerksamkeit von Kognitionspsychologen auf sich. Das typische Verhalten der Mehrheit, das Nichtschalten, kann durch Phänomene erklärt werden, die in der psychologischen Literatur bekannt sind als:
- Der Endowment-Effekt , bei dem Menschen dazu neigen, die Gewinnwahrscheinlichkeit der bereits gewählten – bereits „besessenen“ – Tür zu überschätzen.
- Der Status-Quo-Bias , bei dem die Menschen lieber bei der bereits getroffenen Wahl der Tür bleiben.
- Unterlassungsfehler vs. Provisionsfehler, bei denen unter sonst gleichen Bedingungen Fehler lieber durch Untätigkeit (Stay) als durch Handeln (Switch) gemacht werden.
Experimentelle Beweise bestätigen, dass dies plausible Erklärungen sind, die nicht von der Wahrscheinlichkeitsintuition abhängen. Eine andere Möglichkeit besteht darin, dass sich die Intuition der Menschen einfach nicht mit der Lehrbuchversion des Problems beschäftigt, sondern mit einer echten Spielshow-Einstellung. Dort besteht die Möglichkeit, dass der Showmaster betrügerisch spielt, indem er andere Türen nur dann öffnet, wenn zunächst eine Tür mit dem Auto gewählt wurde. Ein Showmaster, der die Hälfte der Zeiten betrügerisch spielt, modifiziert die Gewinnchancen für den Fall, dass einem angeboten wird, auf "gleiche Wahrscheinlichkeit" umzuschalten.
Kritik an den einfachen Lösungen
Wie bereits erwähnt , lösen die meisten Quellen auf dem Gebiet der Wahrscheinlichkeit , einschließlich vieler einführender Wahrscheinlichkeitslehrbücher, das Problem, indem sie die bedingten Wahrscheinlichkeiten zeigen, dass sich das Auto hinter Tür 1 und Tür 2 befindet1/3 und 2/3 (nicht 1/2 und 1/2) vorausgesetzt, dass der Kandidat zunächst Tür 1 wählt und der Gastgeber Tür 3 öffnet; verschiedene Möglichkeiten, dieses Ergebnis abzuleiten und zu verstehen, wurden in den vorherigen Unterabschnitten beschrieben.
Unter diesen Quellen befinden sich mehrere, die die im Volksmund präsentierten "einfachen" Lösungen ausdrücklich kritisieren und sagen, dass diese Lösungen "richtig, aber ... wackelig" seien oder "das gestellte Problem nicht angehen", oder "unvollständig" seien oder "nicht überzeugend und" seien irreführend" oder sind (am unverblümtsten) "falsch".
Sasha Voloch (2015) schrieb, dass "jede Erklärung, die so etwas wie 'die Wahrscheinlichkeit von Tür 1' 1/3, und nichts kann das ändern ...' ist automatisch faul: Wahrscheinlichkeiten sind Ausdruck unserer Ignoranz über die Welt, und neue Informationen können das Ausmaß unserer Ignoranz ändern."
Manche sagen, dass diese Lösungen eine etwas andere Frage beantworten – eine Formulierung lautet: „Sie müssen vor dem Öffnen einer Tür ankündigen, ob Sie einen Wechsel planen“.
Die einfachen Lösungen zeigen auf verschiedene Weise, dass ein wechselwilliger Teilnehmer mit Wahrscheinlichkeit das Auto gewinnt 2/3, und daher ist das Wechseln die Gewinnstrategie, wenn der Spieler im Voraus zwischen "immer wechseln" und "immer bleiben" wählen muss. Jedoch ist die Gewinnwahrscheinlichkeit durch ständiges Umschalten ein logisch verschiedenes Konzept von der Gewinnwahrscheinlichkeit durch Umschalten, vorausgesetzt, dass der Spieler Tür 1 ausgewählt hat und der Host Tür 3 geöffnet hat . Wie eine Quelle sagt, "scheint die Unterscheidung zwischen [diesen Fragen] viele zu verwirren". Dass diese unterschiedlich sind, lässt sich zeigen, indem man das Problem so variiert, dass diese beiden Wahrscheinlichkeiten unterschiedliche Zahlenwerte haben. Nehmen wir zum Beispiel an, der Kandidat weiß, dass Monty nicht zufällig die zweite Tür unter allen legalen Alternativen auswählt, sondern stattdessen, wenn er die Möglichkeit hat, zwischen zwei verlorenen Türen zu wählen, Monty die rechte öffnet. In dieser Situation haben die folgenden beiden Fragen unterschiedliche Antworten:
- Wie hoch ist die Wahrscheinlichkeit, das Auto zu gewinnen, wenn man immer wechselt?
- Wie groß ist die Wahrscheinlichkeit, das Auto zu gewinnen, wenn der Spieler Tür 1 ausgewählt hat und der Gastgeber Tür 3 geöffnet hat ?
Die Antwort auf die erste Frage lautet 2/3, wie die "einfachen" Lösungen richtig zeigen. Aber die Antwort auf die zweite Frage ist jetzt anders: Die bedingte Wahrscheinlichkeit, dass sich das Auto hinter Tür 1 oder Tür 2 befindet, wenn der Gastgeber Tür 3 (die Tür rechts) geöffnet hat, ist1/2. Dies liegt daran, dass Montys Vorliebe für Türen ganz rechts bedeutet, dass er Tür 3 öffnet, wenn sich das Auto hinter Tür 1 befindet (was ursprünglich mit Wahrscheinlichkeit der Fall ist)1/3) oder wenn das Auto hinter Tür 2 steht (auch ursprünglich mit Wahrscheinlichkeit 1/3). Für diese Variante ergeben die beiden Fragen unterschiedliche Antworten. Solange jedoch die anfängliche Wahrscheinlichkeit, dass sich das Auto hinter jeder Tür befindet, beträgt1/3, es ist nie zum Nachteil des Teilnehmers zu wechseln, da die bedingte Gewinnwahrscheinlichkeit durch Wechseln immer mindestens ist 1/2.
Bei Morganet al. , veröffentlichten vier Universitätsprofessoren einen Artikel in The American Statistician, in dem sie behaupteten, vos Savant habe den richtigen Rat, aber das falsche Argument gegeben. Sie glaubten, dass die Frage nach der Chance auf das Auto hinter Tür 2 gestellt wurde, wenn der Spieler die erste Wahl für Tür 1 und die geöffnete Tür 3 getroffen hatte, und sie zeigten, dass diese Chance alles dazwischen war1/2und 1 abhängig vom Entscheidungsprozess des Gastgebers, der die Wahl hat. Nur wenn die Entscheidung vollständig zufällig ist, ist die Chance2/3.
In einem eingeladenen Kommentar und in nachfolgenden Briefen an den Herausgeber wurden Morgan et al. von einigen Autoren unterstützt, von anderen kritisiert; jeweils eine Antwort von Morgan et al. wird zusammen mit dem Schreiben oder Kommentar in The American Statistician veröffentlicht . Vor allem vos Savant verteidigte sich energisch. Morgan et al. beschwerten sich in ihrer Antwort an vos Savant, dass vos Savant immer noch nicht auf ihren eigenen Hauptpunkt reagiert habe. Später in ihrer Antwort an Hogbin und Nijdam stimmten sie darin überein, dass es natürlich anzunehmen war, dass der Gastgeber eine Tür wählt, die sich völlig zufällig öffnet, wenn er die Wahl hat, und dass daher die bedingte Wahrscheinlichkeit des Gewinnens durch Wechseln (dh bedingt in der Situation, in der sich der Spieler befindet, wenn er seine Wahl treffen muss) denselben Wert hat,2/3, als unbedingte Gewinnwahrscheinlichkeit durch Umschalten (dh gemittelt über alle möglichen Situationen). Diese Gleichheit wurde bereits von Bell (1992) betont, der darauf hinwies, dass die mathematisch komplizierte Lösung von Morgan et al. nur Statistiker ansprechen würde, während die Äquivalenz der bedingten und unbedingten Lösungen im Fall der Symmetrie intuitiv offensichtlich war.
In der Literatur herrscht Uneinigkeit darüber, ob die Formulierung des Problems von vos Savant, wie sie in Parade präsentiert wird, die erste oder zweite Frage stellt und ob dieser Unterschied signifikant ist. Behrends folgert: "Man muss die Sache sorgfältig prüfen, um zu sehen, dass beide Analysen richtig sind"; was nicht heißen soll, dass sie gleich sind. Mehrere Kritiker des Papiers von Morgan et al. , deren Beiträge neben dem Originalpapier veröffentlicht wurden, kritisierte die Autoren, den Wortlaut von vos Savant geändert und ihre Absicht falsch interpretiert zu haben. Ein Diskutant (William Bell) hielt es für Geschmackssache, ob man explizit erwähnt, dass (unter den Standardbedingungen) welche Tür vom Gastgeber geöffnet wird, unabhängig davon ist, ob man wechseln möchte.
Unter den einfachen Lösungen kommt die "Kombinierte Türen-Lösung" einer bedingten Lösung am nächsten, wie wir in der Diskussion der Ansätze mit dem Konzept der Odds und des Bayes-Theorems gesehen haben. Es basiert auf der tief verwurzelten Intuition, dass das Aufdecken von Informationen, die bereits bekannt sind, die Wahrscheinlichkeiten nicht beeinflusst . Zu wissen, dass der Gastgeber eine der beiden nicht ausgewählten Türen öffnen kann, um eine Ziege zu zeigen, bedeutet jedoch nicht, dass das Öffnen einer bestimmten Tür die Wahrscheinlichkeit, dass sich das Auto hinter der ursprünglich gewählten Tür befindet, nicht beeinflusst. Der Punkt ist, obwohl wir im Voraus wissen, dass der Gastgeber eine Tür öffnet und eine Ziege enthüllt, wissen wir nicht, welche Tür er öffnen wird. Wählt der Gastgeber gleichmäßig zufällig zwischen Türen, die eine Ziege verstecken (wie es in der Standardinterpretation der Fall ist), bleibt diese Wahrscheinlichkeit zwar unverändert, kann der Gastgeber jedoch nicht zufällig zwischen solchen Türen wählen, dann die spezifische Tür, die der Gastgeber öffnet gibt zusätzliche Informationen preis. Der Gastgeber kann immer eine Tür öffnen, die eine Ziege enthüllt, und (in der Standardinterpretation des Problems) ändert sich die Wahrscheinlichkeit, dass sich das Auto hinter der ursprünglich gewählten Tür befindet, nicht, aber letzteres ist nicht wegen ersterer wahr. Lösungen, die auf der Behauptung basieren, dass die Handlungen des Gastgebers die Wahrscheinlichkeit, dass sich das Auto hinter dem ursprünglich gewählten Fahrzeug befindet, nicht beeinflussen können, erscheinen überzeugend, aber die Behauptung ist einfach unwahr, es sei denn, jede der beiden Entscheidungen des Gastgebers ist gleich wahrscheinlich, wenn er eine Wahl hat. Die Behauptung ist daher zu begründen; ohne Begründung ist die Lösung bestenfalls unvollständig. Die Antwort kann richtig sein, aber die Begründung, mit der sie begründet wurde, ist mangelhaft.
Lösungen mit bedingter Wahrscheinlichkeit und andere Lösungen
Die einfachen Lösungen oben zeigen, dass ein Spieler mit einer Wechselstrategie das Auto mit Gesamtwahrscheinlichkeit gewinnt 2/3, dh ohne Rücksicht darauf, welche Tür vom Host geöffnet wurde. Im Gegensatz dazu berechnen die meisten Quellen im Bereich der Wahrscheinlichkeit die bedingten Wahrscheinlichkeiten, dass sich das Auto hinter Tür 1 befindet und Tür 2 ist1/3 und 2/3 gegeben, der Teilnehmer wählt zunächst Tür 1 und der Gastgeber öffnet Tür 3. Die Lösungen in diesem Abschnitt betrachten nur die Fälle, in denen der Spieler Tür 1 ausgewählt und der Gastgeber Tür 3 geöffnet hat.
Die einfache Lösung verfeinern
Wenn wir davon ausgehen, dass der Gastgeber willkürlich eine Tür öffnet, dann gibt uns die Tür, die der Gastgeber öffnet, bei der Auswahl überhaupt keine Information darüber, ob sich das Auto hinter Tür 1 befindet oder nicht. Bei den einfachen Lösungen haben wir bereits beobachtet dass die Wahrscheinlichkeit, dass sich das Auto hinter Tür 1 befindet, der ursprünglich vom Spieler gewählten Tür, zunächst 1/3. Darüber hinaus wird der Host sicherlich eine (andere) Tür öffnen, so dass das Öffnen einer Tür ( welche Tür nicht näher bezeichnet) dies nicht ändert.1/3muss die durchschnittliche Wahrscheinlichkeit sein, dass sich das Auto bei der vom Host ausgewählten Tür 2 und der vom Host ausgewählten Tür 3 hinter Tür 1 befindet, da dies die einzigen beiden Möglichkeiten sind. Aber diese beiden Wahrscheinlichkeiten sind gleich. Daher sind beide gleich1/3. Dies zeigt, dass die Wahrscheinlichkeit, dass sich das Auto hinter Tür 1 befindet, wenn der Spieler ursprünglich diese Tür gewählt hat und der Gastgeber Tür 3 geöffnet hat, ist1/3, und daraus folgt, dass die Wahrscheinlichkeit, dass sich das Auto hinter Tür 2 befindet, wenn der Spieler ursprünglich Tür 1 gewählt hat und der Gastgeber Tür 3 geöffnet hat, ist 2/3. Die Analyse zeigt auch, dass die Gesamterfolgsrate von2/3, die durch ständiges Umschalten erreicht wird , nicht verbessert werden kann und unterstreicht, was bereits intuitiv offensichtlich war: Die Wahl, die der Spieler hat, ist die zwischen der ursprünglich gewählten Tür und der anderen Tür, die vom Gastgeber geschlossen bleibt, die spezifischen Zahlen auf diesen Türen sind irrelevant.
Bedingte Wahrscheinlichkeit durch direkte Berechnung
Per Definition ist die bedingte Wahrscheinlichkeit des Gewinnens durch Umschalten, wenn der Teilnehmer anfänglich Tür 1 wählt und der Gastgeber Tür 3 öffnet, die Wahrscheinlichkeit für das Ereignis „Auto ist hinter Tür 2 und Gastgeber öffnet Tür 3“ geteilt durch die Wahrscheinlichkeit für „Gastgeber öffnet Tür 3". Diese Wahrscheinlichkeiten können unter Bezugnahme auf die untenstehende bedingte Wahrscheinlichkeitstabelle oder auf einen äquivalenten Entscheidungsbaum, wie rechts gezeigt, bestimmt werden. Die bedingte Gewinnwahrscheinlichkeit durch Wechseln ist1/3/1/3 + 1/6, welches ist 2/3.
Die bedingte Wahrscheinlichkeitstabelle unten zeigt, wie 300 Fälle, in denen der Spieler anfänglich Tür 1 wählt, im Durchschnitt entsprechend dem Standort des Autos und der Wahl der Tür zum Öffnen durch den Gastgeber aufgeteilt werden.
Satz von Bayes
Viele Lehrbücher und Artikel über Wahrscheinlichkeit auf dem Gebiet der Wahrscheinlichkeitstheorie leiten die bedingte Wahrscheinlichkeitslösung durch eine formale Anwendung des Satzes von Bayes ab ; darunter Bücher von Gill und Henze. Die Verwendung der Odds- Form des Bayes-Theorems, oft als Bayes-Regel bezeichnet, macht eine solche Ableitung transparenter.
Am Anfang steht das Auto mit gleicher Wahrscheinlichkeit hinter einer der drei Türen: Die Quoten für Tür 1, Tür 2 und Tür 3 sind 1 : 1 : 1 . Dies bleibt der Fall, nachdem der Spieler aus Unabhängigkeit Tür 1 gewählt hat. Nach der Bayes-Regel sind die Posterior-Quoten auf den Standort des Autos, vorausgesetzt, der Host öffnet Tür 3, gleich den Prior-Quoten multipliziert mit dem Bayes-Faktor oder der Likelihood, die per Definition die Wahrscheinlichkeit des neuen Spielsteins ist von Informationen (Gastgeber öffnet Tür 3) unter jeder der betrachteten Hypothesen (Standort des Autos). Da der Spieler ursprünglich Tür 1 gewählt hat, beträgt die Chance, dass der Host Tür 3 öffnet, 50%, wenn sich das Auto hinter Tür 1 befindet, 100%, wenn sich das Auto hinter Tür 2 befindet, 0%, wenn sich das Auto hinter Tür 3 befindet der Bayes-Faktor besteht aus den Verhältnissen1/2 : 1 : 0 oder entsprechend 1 : 2 : 0 , während die vorherigen Quoten 1 : 1 : 1 waren . Somit werden die Posterior Odds gleich dem Bayes-Faktor 1 : 2 : 0 . Da der Host Tür 3 geöffnet hat, ist die Wahrscheinlichkeit, dass sich das Auto hinter Tür 3 befindet, null, und es ist doppelt so wahrscheinlich, dass es sich hinter Tür 2 befindet als Tür 1.
Richard Gill analysiert die Wahrscheinlichkeit, dass der Gastgeber Tür 3 öffnet, wie folgt. Da sich das Auto nicht hinter Tür 1 befindet, ist es genauso wahrscheinlich, dass es sich hinter Tür 2 oder 3 befindet. Daher beträgt die Wahrscheinlichkeit, dass der Host Tür 3 öffnet, 50%. Da sich das Auto hinter Tür 1 befindet, beträgt die Wahrscheinlichkeit, dass der Gastgeber Tür 3 öffnet, ebenfalls 50 %, da, wenn der Gastgeber eine Wahl hat, jede Wahl gleich wahrscheinlich ist. Daher beträgt die Wahrscheinlichkeit, dass der Host die Tür 3 öffnet, unabhängig davon, ob sich das Auto hinter Tür 1 befindet oder nicht, 50%. Die Information "Host öffnet Tür 3" trägt einen Bayes-Faktor oder ein Wahrscheinlichkeitsverhältnis von 1 : 1 dazu bei , ob sich das Auto hinter Tür 1 befindet oder nicht. Anfänglich waren die Chancen, dass Tür 1 das Auto verbirgt, 2 : 1 . Daher bleiben die Posterior-Quoten gegen Tür 1, die das Auto verstecken, die gleichen wie die vorherigen Quoten, 2 : 1 .
Mit Worten, die Information, welche Tür vom Gastgeber geöffnet wird (Tür 2 oder Tür 3?) gibt überhaupt keine Auskunft darüber, ob sich das Auto hinter Tür 1 befindet oder nicht, und genau dies wird von Anhängern von . als intuitiv offensichtlich angesehen einfache Lösungen, oder unter Verwendung der Redewendungen mathematischer Beweise, "offensichtlich wahr, durch Symmetrie".
Direkte Berechnung
Man betrachte das Ereignis Ci , das anzeigt, dass sich das Auto hinter der Türnummer i befindet , den Wert Xi für die Auswahl des Spielers und den Wert Hi für das Öffnen der Tür durch den Host annimmt . Der Spieler wählt zunächst Tür i = 1, C = X1 und der Gastgeber öffnet Tür i = 3, C = H3.
In diesem Fall haben wir:
P(H3|X1) = 1/2, weil dieser Ausdruck nur von X1 abhängt , nicht von irgendeinem Ci . In diesem speziellen Ausdruck hängt die Wahl des Hosts also nicht davon ab, wo sich das Auto befindet, und es bleiben nur noch zwei Türen übrig, sobald X1 gewählt wurde (zum Beispiel P(H1|X1) = 0 ); und P(Ci,Xi) = P(Ci)P(Xi), weil Ci und Xi unabhängige Ereignisse sind (der Spieler weiß nicht, wo sich das Auto befindet, um eine Wahl zu treffen).
Wenn der Spieler dann zunächst Tür 1 auswählt und der Gastgeber Tür 3 öffnet, beweisen wir, dass die bedingte Gewinnwahrscheinlichkeit durch Umschalten ist:
Aus der Bayes'schen Regel wissen wir, dass P(A,B) = P(A|B)P(B) = P(B|A)P(A) . Wenn wir diese Logik auf mehrere Ereignisse ausdehnen, zum Beispiel A , B und C , erhalten wir, dass wir mit den verschiedenen Teilmengen von {A, B, C} spielen können , um die Wahrscheinlichkeit der Schnittmenge zu berechnen, als Werkzeug zur Vereinfachung der Berechnung unserer bedingte Wahrscheinlichkeit:
Da wir in unserem Fall wissen, dass P(H3|C2,X1) = 1 ist , haben wir Glück:
Strategische Dominanzlösung
Um auf Nalebuff zurückzukommen, wird das Monty-Hall-Problem auch in der Literatur zur Spieltheorie und Entscheidungstheorie viel untersucht , und auch einige populäre Lösungen entsprechen dieser Sichtweise. Vos Savant bittet um eine Entscheidung, keine Chance. Und die zufälligen Aspekte, wie das Auto versteckt wird und wie eine nicht gewählte Tür geöffnet wird, sind unbekannt. Aus dieser Sicht muss man bedenken, dass der Spieler zwei Möglichkeiten hat, Entscheidungen zu treffen: erstens, welche Tür er anfangs wählen soll; und zweitens, ob gewechselt werden soll oder nicht. Da er nicht weiß, wie das Auto versteckt ist und wie der Moderator Entscheidungen trifft, kann er möglicherweise seine erste Wahlmöglichkeit nutzen, um sozusagen die Aktionen des Teams, das die Quizshow leitet, einschließlich des Gastgebers, zu neutralisieren.
Nach Gill beinhaltet eine Kandidat- Strategie zwei Aktionen: die anfängliche Wahl einer Tür und die Entscheidung zu wechseln (oder zu bleiben), die sowohl von der ursprünglich gewählten Tür als auch von der Tür abhängen kann, zu der der Gastgeber das Umschalten anbietet. Die Strategie eines Teilnehmers ist zum Beispiel "Wähle Tür 1, dann wechsle zu Tür 2, wenn sie angeboten wird, und wechsle nicht zu Tür 3, wenn sie angeboten wird". Zwölf solcher deterministischen Strategien des Kandidaten existieren.
Ein elementarer Vergleich der Strategien des Teilnehmers zeigt, dass es für jede Strategie A eine andere Strategie B gibt, die diese dominiert. Egal wie das Auto versteckt ist und egal welche Regel der Gastgeber verwendet, wenn er die Wahl zwischen zwei Ziegen hat, wenn A das Auto gewinnt, dann gewinnt auch B. Strategie A „Pick Tür 1 dann immer dabei bleiben“ wird von der Strategie B „Pick Tür 1 dann immer wechseln, nachdem der Gastgeber eine Tür aufdeckt“ dominiert: A gewinnt, wenn Tür 1 das Auto verbirgt, B gewinnt, wenn eins der Türen 2 und 3 verbirgt das Auto. In ähnlicher Weise wird Strategie A „Tür 1 aufpicken, dann auf Tür 2 wechseln (falls angeboten), aber nicht auf Tür 3 wechseln (falls angeboten)“ von der Strategie B „Tür 3 aufpicken, dann immer wechseln“ dominiert.
Dominanz ist ein starker Grund, unter den immer wechselnden Strategien nach einer Lösung zu suchen, unter ziemlich allgemeinen Annahmen über die Umgebung, in der der Teilnehmer seine Entscheidungen trifft. Insbesondere wenn das Auto durch eine Randomisierungsvorrichtung versteckt wird – wie das Werfen eines symmetrischen oder asymmetrischen dreiseitigen Würfels – impliziert die Dominanz, dass eine Strategie, die die Wahrscheinlichkeit des Gewinns des Autos maximiert, zu den drei immer wechselnden Strategien gehört, nämlich sei die Strategie, die zunächst die am wenigsten wahrscheinliche Tür auswählt und dann wechselt, unabhängig davon, welche Tür der Host zum Umschalten anbietet.
Strategische Dominanz verbindet das Monty-Hall-Problem mit der Spieltheorie . Im Nullsummenspiel von Gill reduziert das Verwerfen der Nicht-Schaltstrategien das Spiel auf die folgende einfache Variante: Der Moderator (oder das TV-Team) entscheidet sich für die Tür, um das Auto zu verstecken, und der Kandidat wählt zwei Türen ( dh die zwei verbleibenden Türen nach der ersten nominellen Wahl des Spielers). Die Kandidatin gewinnt (und ihr Gegner verliert), wenn sich das Auto hinter einer der beiden von ihr gewählten Türen befindet.
Lösungen durch Simulation
Ein einfacher Weg, um zu zeigen, dass eine Wechselstrategie mit den Standardannahmen wirklich zwei von drei Mal gewinnt, besteht darin, das Spiel mit Spielkarten zu simulieren . Drei Karten aus einem gewöhnlichen Deck werden verwendet, um die drei Türen darzustellen; eine 'besondere' Karte repräsentiert die Tür mit dem Auto und zwei andere Karten repräsentieren die Ziegentüren.
Die Simulation kann mehrmals wiederholt werden, um mehrere Spielrunden zu simulieren. Der Spieler wählt eine der drei Karten aus, dann wirft der „Wirt“ eine Ziegenkarte ab, indem er sich die verbleibenden zwei Karten ansieht. Wenn die verbleibende Karte in der Hand des Gastgebers die Autokarte ist, wird dies als Wechselgewinn verbucht; Wenn der Gastgeber eine Ziegenkarte hält, wird die Runde als bleibender Gewinn gewertet. Da dieses Experiment über mehrere Runden wiederholt wird, nähert sich die beobachtete Gewinnrate für jede Strategie wahrscheinlich ihrer theoretischen Gewinnwahrscheinlichkeit gemäß dem Gesetz der großen Zahlen an .
Wiederholte Spiele machen auch klarer, warum Wechseln die bessere Strategie ist. Nachdem der Spieler seine Karte gezogen hat, steht bereits fest, ob der Wechsel für den Spieler die Runde gewinnt. Sollte dies nicht überzeugen, kann die Simulation mit dem gesamten Deck durchgeführt werden. Bei dieser Variante geht die Autokarte 51 von 52 Mal an den Host und bleibt beim Host, egal wie viele Nicht- Autokarten abgeworfen werden.
Varianten
Eine gängige Variante des Problems, die von mehreren wissenschaftlichen Autoren als kanonisches Problem angenommen wird, macht nicht die vereinfachende Annahme, dass der Gastgeber die zu öffnende Tür einheitlich wählen muss, sondern dass er eine andere Strategie verfolgt . Die Verwirrung darüber, welche Formalisierung maßgebend ist, hat zu beträchtlicher Schärfe geführt, insbesondere weil diese Variante die Beweise komplizierter macht, ohne die Optimalität der Always-Switch-Strategie für den Spieler zu ändern. Bei dieser Variante kann der Spieler je nach beobachteter Wahl des Gastgebers unterschiedliche Gewinnwahrscheinlichkeiten haben , aber in jedem Fall beträgt die Gewinnwahrscheinlichkeit durch Wechseln mindestens1/2(und kann bis zu 1 betragen), während die Gesamtwahrscheinlichkeit des Gewinnens durch Wechseln immer noch genau ist2/3. Die Varianten werden manchmal nacheinander in Lehrbüchern und Artikeln vorgestellt, die die Grundlagen der Wahrscheinlichkeits- und Spieltheorie vermitteln sollen . Eine beträchtliche Anzahl anderer Verallgemeinerungen wurde ebenfalls untersucht.
Andere Verhaltensweisen des Gastgebers
Die 1990 in Parade veröffentlichte Version des Monty-Hall-Problems besagte nicht ausdrücklich, dass der Gastgeber immer eine andere Tür öffnet oder immer die Wahl zum Wechseln anbietet oder sogar nie die Tür öffnet, die das Auto freigibt. vos Savant stellte jedoch in ihrer zweiten Folgekolumne klar, dass nur das Verhalten des beabsichtigten Gastgebers zu der2/3Wahrscheinlichkeit gab sie als ihre ursprüngliche Antwort an. "Alles andere ist eine andere Frage." "So gut wie alle meine Kritiker verstanden das beabsichtigte Szenario. Ich persönlich las fast dreitausend Briefe (von den vielen zusätzlichen Tausenden, die eintrafen) und stellte fest, dass fast jeder einfach darauf bestand, dass die Chancen standen, weil zwei Optionen übrig blieben (oder ein gleichwertiger Fehler). sogar. Nur sehr wenige stellten Fragen zur Mehrdeutigkeit, und die tatsächlich in der Kolumne veröffentlichten Briefe gehörten nicht zu diesen wenigen.“ Die Antwort folgt, wenn das Auto zufällig hinter einer Tür platziert wird, der Gastgeber muss eine Tür öffnen, die eine Ziege enthüllt, unabhängig von der ursprünglichen Wahl des Spielers, und wenn zwei Türen verfügbar sind, wählt er zufällig aus, welche Tür er öffnet. Die folgende Tabelle zeigt eine Vielzahl anderer möglicher Host-Verhaltensweisen und die Auswirkungen auf den Erfolg des Wechsels.
Die Bestimmung der besten Strategie des Spielers innerhalb eines bestimmten Satzes anderer Regeln, die der Gastgeber befolgen muss, ist die Art von Problem, die in der Spieltheorie untersucht wird . Wenn der Host zum Beispiel das Angebot zum Wechseln nicht machen muss, kann der Spieler den Verdacht haben, dass der Host böswillig ist und macht die Angebote häufiger, wenn der Spieler ursprünglich das Auto ausgewählt hat. Im Allgemeinen hängt die Antwort auf diese Art von Frage von den spezifischen Annahmen ab, die über das Verhalten des Hosts gemacht werden, und kann von „Ignoriere den Host vollständig“ bis „eine Münze werfen und wechseln, wenn sie Kopf zeigt“ reichen; siehe letzte Zeile der Tabelle unten.
Morgan et al und Gillman zeigen beide eine allgemeinere Lösung, bei der das Auto (gleichmäßig) zufällig platziert wird, der Host jedoch nicht gezwungen ist, gleichmäßig zufällig auszuwählen, wenn der Spieler das Auto ursprünglich ausgewählt hat, so interpretieren beide die Problemstellung in Parade trotz der Haftungsausschlüsse des Autors. Beide änderten den Wortlaut der Parade- Version, um diesen Punkt zu betonen, als sie das Problem erneut formulierten. Sie betrachten ein Szenario, in dem der Wirt entscheidet, zwei Ziegen mit einer Präferenz, ausgedrückt als Wahrscheinlichkeit q , mit einem Wert zwischen 0 und 1 zu enthüllen. Wenn der Wirt zufällig wählt, wäre q1/2 und Wechsel gewinnt mit Wahrscheinlichkeit 2/3unabhängig davon, welche Tür der Gastgeber öffnet. Wenn der Spieler Tür 1 wählt und die Präferenz des Gastgebers für Tür 3 ist q , dann ist die Wahrscheinlichkeit, dass der Gastgeber Tür 3 öffnet und das Auto sich hinter Tür 2 befindet1/3, während die Wahrscheinlichkeit, dass der Gastgeber Tür 3 öffnet und sich das Auto hinter Tür 1 befindet, Q/3. Dies sind die einzigen Fälle , in denen die Host - Tür öffnet 3, so dass die bedingte Wahrscheinlichkeit des Gewinnens durch Umschalten des Host gegeben öffnet Tür 3 ist1/3/1/3 + q /3 was vereinfacht zu 1/1 + q. Da q zwischen 0 und 1 variieren kann, kann diese bedingte Wahrscheinlichkeit zwischen1/2und 1. Dies bedeutet, selbst ohne den Host zu zwingen, zufällig auszuwählen, wenn der Spieler anfänglich das Auto auswählt, ist der Spieler beim Umschalten nie schlechter dran. Keine Quelle schlägt jedoch vor, dass der Spieler den Wert von q kennt, sodass der Spieler keine andere Wahrscheinlichkeit als die zuschreiben kann2/3 was vos Savant als implizit annahm.
| Mögliches Hostverhalten bei nicht näher bezeichnetem Problem | |
|---|---|
| Host-Verhalten | Ergebnis |
| Der Host verhält sich wie in der spezifischen Version des Problems angegeben. | Das Schalten gewinnt das Auto in zwei Drittel der Fälle. (Sonderfall der verallgemeinerten Form unten mit p = q = 1/2) |
| Der Wirt enthüllt immer eine Ziege und bietet immer einen Schalter an. Wenn er die Wahl hat, wählt er die Ziege ganz links mit Wahrscheinlichkeit p (die von der anfänglichen Wahl des Spielers abhängen kann) und die ganz rechte Tür mit Wahrscheinlichkeit q = 1 − p . | Wenn der Host die Tür ganz rechts öffnet, gewinnt das Umschalten mit Wahrscheinlichkeit 1/(1+ q ). |
| "Monty from Hell": Der Host bietet die Option zum Wechseln nur an, wenn die erste Wahl des Spielers das gewinnende Tor ist. | Wechseln bringt immer eine Ziege. |
| „Mind-reading Monty“: Der Gastgeber bietet die Möglichkeit zu wechseln, falls der Gast trotzdem bleiben will oder der Gast auf eine Ziege umsteigt. | Wechseln bringt immer eine Ziege. |
| "Angelic Monty": Der Host bietet die Option zum Wechseln nur an, wenn der Spieler eine falsche Auswahl getroffen hat. | Das Schalten gewinnt immer das Auto. |
| "Monty Fall" oder "Ignorant Monty": Der Gastgeber weiß nicht, was sich hinter den Türen verbirgt, und öffnet zufällig eine, die das Auto nicht preisgibt. | Beim Wechseln gewinnt das Auto die Hälfte der Zeit. |
| Der Gastgeber weiß, was sich hinter den Türen verbirgt, und wählt (vor der Wahl des Spielers) zufällig aus, welche Ziege er aufdecken möchte. Er bietet die Option zum Wechseln nur an, wenn die Wahl des Spielers von seiner abweicht. | Beim Wechseln gewinnt das Auto die Hälfte der Zeit. |
| Der Gastgeber öffnet eine Tür und bietet an, 100 % der Zeit zu wechseln, wenn der Kandidat das Auto ursprünglich ausgewählt hat, und ansonsten 50 % der Zeit. | Wechsel gewinnt 1/2die Zeit im Nash-Gleichgewicht . |
| Vierstufige Spieltheorie für zwei Spieler. Der Spieler spielt gegen den Show-Organisator (TV-Sender), zu dem auch der Moderator gehört. Erste Phase: Die Organisatoren wählen eine Tür (Auswahl wird vom Spieler geheim gehalten). Zweite Phase: Der Spieler trifft eine vorläufige Wahl der Tür. Dritte Stufe: Gastgeber öffnet eine Tür. Vierte Phase: Der Spieler trifft eine endgültige Wahl. Der Spieler will das Auto gewinnen, der TV-Sender will es behalten. Dies ist ein Nullsummenspiel für zwei Personen. Nach dem Satz von Neumann aus der Spieltheorie existiert eine Minimax-Lösung oder ein Nash-Gleichgewicht , wenn wir beiden Parteien vollständig randomisierte Strategien erlauben . | Minimax-Lösung ( Nash-Gleichgewicht ): Das Auto wird zuerst zufällig zufällig versteckt und der Host wählt später eine einheitliche zufällige Tür zum Öffnen, ohne das Auto zu offenbaren und sich von der Tür des Spielers zu unterscheiden; Der Spieler wählt zuerst eine einheitliche zufällige Tür und wechselt später immer zu einer anderen geschlossenen Tür. Mit seiner Strategie hat der Spieler eine Gewinnchance von mindestens2/3, aber der TV-Sender spielt; Mit der Strategie des TV-Senders wird der TV-Sender mit Wahrscheinlichkeit höchstens verlieren2/3, jedoch spielt der Spieler. Die Tatsache, dass diese beiden Strategien übereinstimmen (mindestens2/3, höchstens 2/3) beweist, dass sie die Minimax-Lösung bilden. |
| Wie zuvor, aber jetzt hat der Gastgeber die Möglichkeit, eine Tür überhaupt nicht zu öffnen. | Minimax-Lösung ( Nash-Gleichgewicht ): Auto wird zunächst zufällig gleichförmig versteckt und Host öffnet später nie eine Tür; Spieler wählt zuerst eine Tür gleichmäßig zufällig und wechselt später nie. Die Strategie des Spielers garantiert eine Gewinnchance von mindestens1/3. Die Strategie des TV-Senders garantiert eine Verlustchance von höchstens1/3. |
| Deal or No Deal- Fall: Der Host fordert den Spieler auf, eine Tür zu öffnen, und bietet dann einen Schalter an, falls das Auto nicht aufgedeckt wurde. | Beim Wechseln gewinnt das Auto die Hälfte der Zeit. |
N Türen
DL Ferguson (1975 in einem Brief an Selvin) schlägt eine N- Tür-Verallgemeinerung des ursprünglichen Problems vor, bei der der Gastgeber p Verlusttüren öffnet und dann dem Spieler die Möglichkeit bietet, zu wechseln; bei dieser Variante gewinnt das Schalten mit Wahrscheinlichkeit . Diese Wahrscheinlichkeit ist immer größer als , daher bringt das Umschalten immer einen Vorteil.
Auch wenn der Gastgeber nur eine einzige Tür öffnet ( ), ist der Spieler in jedem Fall besser dran. Wenn N größer wird, nimmt der Vorteil ab und geht gegen Null. Im anderen Extremfall, wenn der Host alle verlierenden Türen außer einer öffnet ( p = N − 2), steigt der Vorteil, wenn N größer wird (die Wahrscheinlichkeit, durch Wechsel zu gewinnen, istN − 1/n, die sich 1 annähert, wenn N sehr groß wird).
Quantenversion
Eine Quantenversion des Paradoxons veranschaulicht einige Punkte über die Beziehung zwischen klassischer oder nicht-quantenbasierter Information und Quanteninformation , wie sie in den Zuständen quantenmechanischer Systeme kodiert sind. Die Formulierung basiert lose auf der Quantenspieltheorie . Die drei Türen werden durch ein Quantensystem ersetzt, das drei Alternativen ermöglicht; Das Öffnen einer Tür und der Blick dahinter wird als eine bestimmte Messung übersetzt. Die Regeln können in dieser Sprache angegeben werden, und auch hier hat der Spieler die Wahl, bei der ursprünglichen Wahl zu bleiben oder zu einer anderen "orthogonalen" Option zu wechseln. Die letztgenannte Strategie verdoppelt die Chancen, genau wie im klassischen Fall. Wenn der Moderator der Show jedoch die Position des Preises nicht vollständig quantenmechanisch zufällig ausgewählt hat, kann der Spieler es noch besser machen und kann den Preis manchmal sogar mit Sicherheit gewinnen.
Geschichte
Das früheste von mehreren Wahrscheinlichkeitsrätseln im Zusammenhang mit dem Monty-Hall-Problem ist Bertrands Kastenparadox , das Joseph Bertrand 1889 in seinem Calcul des probabilités aufstellte . In diesem Puzzle gibt es drei Schachteln: eine Schachtel mit zwei Goldmünzen, eine Schachtel mit zwei Silbermünzen und eine Schachtel mit jeweils einer. Nachdem man zufällig eine Schachtel ausgewählt und zufällig eine Münze abgezogen hat, die zufällig eine Goldmünze ist, stellt sich die Frage, wie hoch die Wahrscheinlichkeit ist, dass die andere Münze Gold ist. Wie beim Monty-Hall-Problem lautet die intuitive Antwort1/2, aber die Wahrscheinlichkeit ist tatsächlich 2/3.
Die drei Gefangene Problem , veröffentlicht in Martin Gardner ‚s Mathematical Games Spalte in Scientific American im Jahr 1959 ist mit dem Monty Hall Problem gleichwertig. Dieses Problem betrifft drei verurteilte Gefangene, von denen einer heimlich zur Begnadigung ausgewählt wurde. Einer der Gefangenen bittet den Aufseher, ihm den Namen eines der anderen zu nennen, der hingerichtet werden soll, und argumentiert, dass dies keine Informationen über sein eigenes Schicksal preisgibt, aber seine Chancen auf Begnadigung erhöht1/3 zu 1/2. Der Aufseher verpflichtet sich, (heimlich) eine Münze zu werfen, um zu entscheiden, welchen Namen er angeben soll, wenn der Gefangene, der darum bittet, begnadigt wird. Die Frage ist, ob die Kenntnis der Antwort des Aufsehers die Chancen des Gefangenen auf Begnadigung verändert. Dieses Problem entspricht dem Monty-Hall-Problem; der Gefangene, der die Frage stellt, hat immer noch ein1/3 Chance auf Begnadigung, aber sein namenloser Kollege hat ein 2/3 Chance.
Steve Selvin stellte das Monty-Hall-Problem 1975 in zwei Briefen an The American Statistician . Der erste Brief präsentierte das Problem in einer Version, die seiner Präsentation in Parade 15 Jahre später nahe kam. Die zweite scheint die erste Verwendung des Begriffs "Monty-Hall-Problem" zu sein. Das Problem ist eigentlich eine Extrapolation aus der Spielshow. Monty Hall hat eine falsche Tür zu bauen Aufregung offen, bot aber einen bekannten geringeren Preis - wie $ 100 Cash - eher als eine Wahl Schalter Türen. Wie Monty Hall an Selvin schrieb:
Und wenn Sie jemals in meine Show kommen, halten die Regeln für Sie fest – keine Handelsboxen nach der Auswahl.
— Monty Hall
Eine Version des Problems, die der drei Jahre später in Parade sehr ähnlichen Version sehr ähnlich war, wurde 1987 in der Puzzles-Sektion des Journal of Economic Perspectives veröffentlicht . Nalebuff, als späterer Autor der mathematischen Ökonomie, sieht das Problem als eine einfache und amüsante Übung in der Spieltheorie .
"The Monty Hall Trap", Phillip Martins Artikel von 1989 in Bridge Today , präsentierte Selvins Problem als Beispiel für das, was Martin die Wahrscheinlichkeitsfalle nennt, nicht zufällige Informationen so zu behandeln, als ob sie zufällig wären, und bezieht dies auf Konzepte im Bridge- Spiel .
Eine neu formulierte Version von Selvins Problem erschien im September 1990 in Marilyn vos Savant 's Frage-und-Antwort-Kolumne Ask Marilyn von Parade . Obwohl vos Savant die richtige Antwort gab, dass der Wechsel in zwei Dritteln der Fälle gewinnen würde, schätzt sie, dass das Magazin eingegangen ist 10.000 Briefe, darunter fast 1.000 von Doktoranden unterzeichnet, viele davon auf Briefköpfen von mathematischen und naturwissenschaftlichen Fakultäten, in denen sie erklärten, dass ihre Lösung falsch war. Aufgrund der überwältigenden Resonanz veröffentlichte Parade vier beispiellose Kolumnen zu diesem Problem. Aufgrund der Publizität erhielt das Problem den alternativen Namen "Marilyn and the Goats".
Im November 1990 fand eine ebenso umstrittene Diskussion über den Artikel von vos Savant in Cecil Adams ' Kolumne „ The Straight Dope “ statt. Adams antwortete anfangs falsch, dass die Chancen für die beiden verbleibenden Türen jeweils eins zu zwei sein müssen. Nachdem ein Leser geschrieben hatte, um die Mathematik von Adams' Analyse zu korrigieren, stimmte Adams zu, dass er sich mathematisch geirrt hatte. „Du wählst Tür Nr. 1. Jetzt haben Sie die Wahl: Tür Nr. 1 öffnen oder Tür Nr. 2 und Tür Nr. 3 öffnen. Im letzteren Fall behalten Sie den Preis, wenn er sich hinter einer der Türen befindet zwei zu drei Schüsse auf den Preis als eins zu drei, nicht wahr? Wenn Sie darüber nachdenken, bietet Ihnen das ursprüngliche Problem im Grunde die gleiche Wahl. Monty sagt im Grunde: Sie können Ihre eine Tür behalten oder Sie können die anderen beiden Türen haben, von denen ich eine (eine Nicht-Preis-Tür) für Sie öffnen werde." Adams sagte jedoch, dass die Parade- Version kritische Beschränkungen unausgesprochen ließe, und ohne diese Beschränkungen lagen die Gewinnchancen durch Wechseln nicht unbedingt bei zwei von drei (z. B. war es nicht vernünftig anzunehmen, dass der Gastgeber immer eine Tür öffnet). Zahlreiche Leser schrieben jedoch an, Adams habe "das erste Mal Recht" gehabt und die richtigen Chancen lägen eins zu zwei.
Die Kolumne „ Parade“ und ihre Reaktion erhielten in der Presse große Aufmerksamkeit, darunter eine Titelstory in der New York Times, in der Monty Hall selbst interviewt wurde. Hall verstand das Problem, führte dem Reporter eine Demonstration mit Autoschlüsseln vor und erklärte, wie sich das tatsächliche Spiel bei Let's Make a Deal von den Regeln des Puzzles unterschied. In dem Artikel wies Hall darauf hin, dass die theoretische Lösung nicht auf das eigentliche Gameplay der Show zutraf, da er die Kontrolle über den Fortschritt des Spiels hatte und auf die Psychologie des Teilnehmers spielte. Er sagte, er sei nicht überrascht über die Beharrlichkeit der Experten, dass die Wahrscheinlichkeit bei 1 von 2 liege. "Das ist die gleiche Annahme, die die Teilnehmer in der Show machen würden, nachdem ich ihnen gezeigt habe, dass sich hinter einer Tür nichts befindet", sagte er. „Sie würden denken, dass die Chancen an ihrer Tür jetzt auf 1 zu 2 gestiegen sind, also hassten sie es, die Tür aufzugeben, egal wie viel Geld ich anbot. Indem wir diese Tür öffneten, übten wir Druck aus. Wir nannten es Henry James Behandlung. Es war ' The Turn of the Screw '." Hall stellte klar, dass er als Moderator einer Spielshow nicht die Regeln des Rätsels in der Kolumne vos Savant befolgen muss und einer Person nicht immer die Möglichkeit zum Wechsel geben muss (z verlierende Tür, könnte ihnen Geld anbieten, um nicht von einer verlierenden Tür zu einer gewinnenden Tür zu wechseln, oder ihnen die Möglichkeit geben, nur zu wechseln, wenn sie eine gewinnende Tür hatten). "Wenn der Gastgeber ständig eine Tür öffnen und Ihnen einen Schalter anbieten muss, dann sollten Sie den Schalter nehmen", sagte er. "Aber wenn er die Wahl hat, ob er einen Wechsel zulässt oder nicht, pass auf. Vorbehalte. Es hängt alles von seiner Stimmung ab."
Siehe auch
- MythBusters Folge 177 „Wheel of Mythfortune“ – Pick a Door
- Prinzip der eingeschränkten Auswahl – ähnliche Anwendung der Bayes'schen Aktualisierung in der Vertragsbrücke
Ähnliche Rätsel in der Wahrscheinlichkeits- und Entscheidungstheorie
Verweise
Literaturverzeichnis
- Adams, Cecil (2. November 1990). "Bei Let's Make a Deal wählst du Tür Nr. 1 aus. Monty öffnet Tür Nr. 2 – kein Preis. Bleiben Sie bei Tür Nr. 1 oder wechseln Sie zu Nr. 3?" . Das Straight Dope . Abgerufen am 25. Juli 2005 .
- Barbeau, Edward (1993). „Irrtümer, Fehler und Flimflam: Das Problem des Autos und der Ziegen“. Das College Mathematik Journal . 24 (2): 149–154. doi : 10.1080/07468342.1993.11973519 .
- Behrends, Ehrhard (2008). Fünf-Minuten-Mathematik . AMS Buchhandlung. P. 57. ISBN 978-0-8218-4348-2.
- Bell, William (August 1992). "Kommentar zu Let's make a deal von Morgan et al. " Der amerikanische Statistiker . 46 (3): 241.
- Carlton, Matthew (2005). „Stammbäume, Preise und Gefangene: Der Missbrauch der bedingten Wahrscheinlichkeit“ . Zeitschrift für statistische Bildung . 13 (2). doi : 10.1080/10691898.2005.11910554 . S2CID 118792491 .
- Chun, Junge H. (1991). "Game-Show-Problem". OR/MS heute . 18 (3): 9.
- D'Ariano, GM; Gill, RD; Keyl, M.; Kümmerer, B.; Maassen, H.; Werner, RF (21. Februar 2002). „Das Quanten-Monty-Hall-Problem“. Menge Inf. Berechnen . 2 (5): 355–366. arXiv : quant-ph/0202120 . Bibcode : 2002quant.ph..2120D .
- Devlin, Keith (Juli–August 2003). "Devlin's Angle: Monty Hall" . Die Mathematische Vereinigung von Amerika . Abgerufen am 23. Juni 2014 .
- Devlin, Keith (Dezember 2005). "Devlin's Angle: Monty Hall revisited" . Die Mathematische Vereinigung von Amerika . Abgerufen am 23. Juni 2014 .
- Eisenhauer, Joseph G. (2001). "Die Monty-Hall-Matrix" (PDF) . Unterrichtsstatistik . 22 (1): 17–20. doi : 10.1111/1467-9639.00005 . Archiviert vom Original (PDF) am 1. März 2012 . Abgerufen am 9. Juli 2012 .
- Enßlin, Torsten A.; Westerkamp, Margret (April 2018). „Die Rationalität der Irrationalität im Monty-Hall-Problem“. Annalen der Physik . 531 (3): 1800128. arXiv : 1804.04948 . Bibcode : 2019AnP...53100128E . doi : 10.1002/undp.201800128 . S2CID 56036255 .
- Falk, Ruma (1992). "Ein genauerer Blick auf die Wahrscheinlichkeiten der berüchtigten drei Gefangenen". Erkenntnis . 43 (3): 197–223. doi : 10.1016/0010-0277(92)90012-7 . PMID 1643813 . S2CID 39617738 .
- Flitney, Adrian P. & Abbott, Derek (2002). „Quantenversion des Monty-Hall-Problems“. Physical Review A . 65 (6): 062318. arXiv : quant-ph/0109035 . Bibcode : 2002PhRvA..65f2318F . doi : 10.1103/PhysRevA.65.062318 . S2CID 119417490 . Kunst. 062318, 2002.
- Fox, Craig R. & Levav, Jonathan (2004). "Partition-Edit-Count: Naive Extensional Reasoning bei der Beurteilung der bedingten Wahrscheinlichkeit" (PDF) . Zeitschrift für experimentelle Psychologie: Allgemeines . 133 (4): 626–642. doi : 10.1037/0096-3445.133.4.626 . PMID 15584810 . Archiviert vom Original (PDF) am 10.04.2020.
- Gardner, Martin (Oktober 1959a). "Mathematische Spiele". Wissenschaftlicher Amerikaner : 180–182. Nachgedruckt in The Second Scientific American Book of Mathematical Puzzles and DiversionsCS1-Wartung: Postscript ( Link )
- Gardner, Martin (November 1959b). "Mathematische Spiele". Wissenschaftlicher Amerikaner : 188.
- Gardner, Martin (1982). Aha! Gotcha: Paradoxe zum Rätseln und Entzücken . WH Freeman. ISBN 978-0716713616.
- Gill, Jeff (2002). Bayessche Methoden . CRC-Presse. S. 8–10. ISBN 1-58488-288-3. ( eingeschränkte Online-Kopie , S. 8, bei Google Books )CS1-Wartung: Postscript ( Link )
- Gill, Richard (2010). "Monty-Hall-Problem". Internationale Enzyklopädie der statistischen Wissenschaften . Springer. S. 858–863. arXiv : 1002.3878v2 .
- Gill, Richard (Februar 2011). "Das Monty-Hall-Problem ist kein Wahrscheinlichkeitsrätsel (es ist eine Herausforderung in der mathematischen Modellierung)". Statistica Neerlandica . 65 (1): 58–71. arXiv : 1002.0651v3 . doi : 10.1111/j.1467-9574.2010.00474.x .
- Gill, Richard (17. März 2011a). "Das Monty-Hall-Problem" (PDF) . Mathematisches Institut, Universität Leiden, Niederlande. S. 10–13.
- Gillmann, Leonard (1992). „Das Auto und die Ziegen“. Amerikanische mathematische Monatszeitschrift . 99 (1): 3–7. doi : 10.2307/2324540 . JSTOR 2324540 .
- Gilovich, T.; Medvec, VH & Chen, S. (1995). „Kommission, Unterlassung und Dissonanzreduktion: Bewältigung des Bedauerns im „Monty Hall“-Problem“ . Zeitschrift für Persönlichkeits- und Sozialpsychologie . 21 (2): 182–190. doi : 10.1177/0146167295212008 . S2CID 146500989 .
- Gnedin, Sascha (2011). "Das Mondee Gills-Spiel" . Der Mathematische Intelligenz . 34 : 34–41. doi : 10.1007/s00283-011-9253-0 .
- Granberg, Donald (2014). Das Monty Hall Dilemma: Eine kognitive Illusion par excellence . Lumad/CreateSpace. ISBN 978-0996100809.
- Granberg, Donald (1996). "Umschalten oder nicht wechseln". In vos Savant, Marilyn (Hrsg.). Die Macht des logischen Denkens . St. Martins Presse. ISBN 0-312-30463-3. ( eingeschränkte Online-Kopie , S. 169, bei Google Books )CS1-Wartung: Postscript ( Link )
- Granberg, Donald & Brown, Thad A. (1995). „Das Monty-Hall-Dilemma“. Bulletin für Persönlichkeits- und Sozialpsychologie . 21 (7): 711-729. doi : 10.1177/0146167295217006 . S2CID 146329922 .
- Grinstead, Charles M. & Snell, J. Laurie (4. Juli 2006). Grinstead und Snells Einführung in die Wahrscheinlichkeit (PDF) . Abgerufen am 2. April 2008 .
- Hall, Monty (1975). "Das Monty-Hall-Problem" . LetsMakeADeal.com . Abgerufen am 15. Januar 2007 . Enthält einen Brief vom 12. Mai 1975 an Steve SelvinCS1-Wartung: Postscript ( Link )
- Henze, Norbert (2011) [1997]. Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls (9. Aufl.). Springer. S. 50–51, 105–107. ISBN 978-3834818454. ( eingeschränkte Online-Kopie , S. 105, bei Google Books )CS1-Wartung: Postscript ( Link )
- Herbranson, WT & Schroeder, J. (2010). "Sind Vögel schlauer als Mathematiker? Tauben ( Columba livia ) arbeiten optimal in einer Version des Monty Hall Dilemmas" . Zeitschrift für vergleichende Psychologie . 124 (1): 1–13. doi : 10.1037/a0017703 . PMC 3086893 . PMID 20175592 .
- Hogbin, M.; Nijdam, W. (2010). „Brief an den Herausgeber von Let’s make a deal von Morgan et al “. Der amerikanische Statistiker . 64 (2): 193. doi : 10.1198/tast.2010.09227 . S2CID 219595003 .
- Kahnemann, D. ; Knetsch, JL & Thaler, RH (1991). „Anomalien: Der Stiftungseffekt, Verlustaversion und Status-quo-Bias“ . Zeitschrift für wirtschaftliche Perspektiven . 5 : 193-206. doi : 10.1257/jep.5.1.193 .
- Kaivanto, K.; Kroll, EB & Zabinski, M. (2014). "Bias Trigger Manipulation und Task-Form Understanding in Monty Hall" (PDF) . Wirtschaftsbulletin . 34 (1): 89–98.
- Krauss, Stefan & Wang, XT (2003). „Die Psychologie des Monty-Hall-Problems: Entdeckung psychologischer Mechanismen zur Lösung einer hartnäckigen Denkaufgabe“ (PDF) . Zeitschrift für experimentelle Psychologie: Allgemeines . 132 (1): 3–22. doi : 10.1037/0096-3445.132.1.3 . Abgerufen am 30. März 2008 .
- Lucas, Stephen; Rosenhouse, Jason & Schepler, Andrew (2009). "Das Monty-Hall-Problem, neu überdacht" (PDF) . Mathematik-Magazin . 82 (5): 332–342. doi : 10.4169/002557009X478355 . Abgerufen am 9. Juli 2012 .
- Martin, Philipp (1993) [1989]. Granovetter, Pamela; Granovetter, Matthew (Hrsg.). Die Monty Hall-Falle . Nur für Experten . Granovetter-Bücher.
- Morgan, JP; Chaganty, NR; Dahiya, RC & Doviak, MJ (1991). "Lass uns einen Deal machen: Das Dilemma des Spielers". Der amerikanische Statistiker . 45 (4): 284–287. doi : 10.1080/00031305.1991.104755821 . JSTOR 2684453 .
- Morone, A. & Fiore, A. (2007). "Monty Halls drei Türen für Dummies" . Dipartimento di Scienze Economiche e Metodi Matematici – Università di Bari, Southern Europe Research in Economic Studies – SERIES Working Paper No. 0012.
- Mueser, Peter R. & Granberg, Donald (Mai 1999). "Das Monty Hall Dilemma Revisited: Das Zusammenspiel von Problemdefinition und Entscheidungsfindung verstehen" . Experimentell . Universitätsbibliothek München. Arbeitspapier 99–06 . Abgerufen am 10. Juni 2010 .
- Nalebuff, Barry (Herbst 1987). "Puzzles: Wählen Sie einen Vorhang, Duell, Zwei-Punkte-Konvertierungen und mehr" . Zeitschrift für wirtschaftliche Perspektiven . 1 (2): 157–163. doi : 10.1257/jep.1.2.157 .
- Rao, M. Bhaskara (August 1992). "Kommentar zu Let's make a deal von Morgan et al. " Der amerikanische Statistiker . 46 (3): 241–242.
- Rosenhaus, Jason (2009). Das Monty-Hall-Problem . Oxford University Press. ISBN 978-0-19-536789-8.
- Rosenthal, Jeffrey S. (September 2005a). "Monty Hall, Monty Fall, Monty Crawl" (PDF) . Mathe-Horizonte : 5–7.
- Rosenthal, Jeffrey S. (2005b). Vom Blitz getroffen: Die seltsame Welt der Wahrscheinlichkeiten . Harper Collins. ISBN 978-0-00-200791-7.
- Samuelson, W. & Zeckhauser, R. (1988). „Status-quo-Bias bei der Entscheidungsfindung“. Zeitschrift für Risiko und Unsicherheit . 1 : 7–59. CiteSeerX 10.1.1.632.3193 . doi : 10.1007/bf00055564 . S2CID 5641133 .
- Selvin, Steve (Februar 1975a). "Ein Problem der Wahrscheinlichkeit (Brief an die Redaktion)". Der amerikanische Statistiker . 29 (1): 67–71. doi : 10.1080/00031305.1975.10479121 . JSTOR 2683689 .
- Selvin, Steve (August 1975b). „Über das Monty-Hall-Problem (Brief an die Redaktion)“. Der amerikanische Statistiker . 29 (3): 134. JSTOR 2683443 .
- Seymann, RG (1991). "Kommentar zu Let's Make a Deal : Das Dilemma des Spielers". Der amerikanische Statistiker . 45 (4): 287–288. doi : 10.2307/2684454 . JSTOR 2684454 .
- Stibel, Jeffrey ; Dror, Itiel; Ben-Zeev, Talia (2008). "The Collapsing Choice Theory: Dissoziation von Wahl und Urteil bei der Entscheidungsfindung" (PDF) . Theorie und Entscheidung .
- Tierney, John (21. Juli 1991). "Hinter den Türen von Monty Hall: Rätsel, Debatte und Antwort?" . Die New York Times . Abgerufen am 18. Januar 2008 .
- Vazsonyi, Andrew (Dezember 1998 – Januar 1999). "Welche Tür hat der Cadillac?" (PDF) . Entscheidungslinie : 17–19. Archiviert vom Original (PDF) am 2014-04-13 . Abgerufen am 16. Oktober 2012 .CS1-Wartung: Datum und Jahr ( Link )
- VerBruggen, Robert (24. Februar 2015). "Das 'Monty Hall'-Problem: Jeder liegt falsch" . RealClearScience . Abgerufen 2017-10-12 .
- Volokh, Sasha (2015-03-02). „Eine ‚einfache‘ Antwort auf das berüchtigte Monty-Hall-Problem“ . Die Washington-Post . ISSN 0190-8286 . Abgerufen 2017-10-12 .
- vos Savant, Marilyn (2012) (1990-1991). "Game-Show-Problem" . Parade . Archiviert vom Original am 29. April 2012.
- vos Savant, Marilyn (9. September 1990a). "Fragen Sie Marilyn" . Parade : 16. Archiviert vom Original am 21. Januar 2013 . Abgerufen am 12. November 2012 .
- vos Savant, Marilyn (2. Dezember 1990b). "Fragen Sie Marilyn" . Parade : 25. Archiviert vom Original am 21. Januar 2013 . Abgerufen am 12. November 2012 .
- vos Savant, Marilyn (17. Februar 1991a). "Fragen Sie Marilyn" . Parade : 12. Archiviert vom Original am 21. Januar 2013 . Abgerufen am 12. November 2012 .
- vos Savant, Marilyn (November 1991c). "Die Antwort von Marilyn vos Savant". Leserbriefe. Der amerikanische Statistiker . 45 (4): 347.
- vos Savant, Marilyn (1996). Die Macht des logischen Denkens . St. Martins Presse. P. 5 . ISBN 0-312-15627-8.
- Williams, Richard (2004). "Anhang D: Die Monty Hall-Kontroverse" (PDF) . Kursnotizen für die Soziologie-Absolventenstatistik I . Abgerufen 2008-04-25 .
- Whitaker, Craig F. (9. September 1990). "[Formulierung von Marilyn vos Savant der Frage in einem Brief von Craig Whitaker]. Frag Marilyn". Parade : 16.
Weiterlesen
- Gill, Richard (2011b). "Monty-Hall-Problem (Version 5)" . StatProb: Die von Statistik- und Wahrscheinlichkeitsgesellschaften gesponserte Enzyklopädie . Archiviert vom Original am 2016-01-21 . Abgerufen 2011-04-03 .
- vos Savant, Marilyn (7. Juli 1991b). "Fragen Sie Marilyn" . Parade : 26. Archiviert vom Original am 21. Januar 2013 . Abgerufen am 12. November 2012 .
- vos Savant, Marilyn (26. November 2006). "Fragen Sie Marilyn". Parade : 6.
Externe Links
- Das Game-Show-Problem – die ursprüngliche Frage und Antworten auf der Website von Marilyn vos Savant
- University of California San Diego, Monty kennt Version und Monty kennt keine Version, eine Erklärung des Spiels
- Monty Hall in Curlie
- "Stick oder Switch? Wahrscheinlichkeit und das Monty-Hall-Problem" , BBC News Magazine , 11. September 2013 (Video). Der Mathematiker Marcus du Sautoy erklärt das Monty-Hall-Paradoxon.