Satz von Nielsen-Schreier - Nielsen–Schreier theorem

In der Gruppentheorie , einem Zweig der Mathematik, besagt der Nielsen-Schreier-Satz , dass jede Untergruppe einer freien Gruppe selbst frei ist. Es ist nach Jakob Nielsen und Otto Schreier benannt .

Aussage des Theorems

Eine freie Gruppe kann aus einer Gruppenpräsentation definiert werden, die aus einem Satz von Generatoren ohne Beziehungen besteht. Das heißt, jedes Element ist ein Produkt einer Folge von Generatoren und ihren Umkehrungen, aber diese Elemente gehorchen keinen Gleichungen außer denen, die trivial aus gg −1 = 1 folgen . Die Elemente einer freien Gruppe können als alle möglichen reduzierten Wörter beschrieben werden , die Strings von Generatoren und ihre Inversen, in denen kein Generator an seinen eigenen Inversen angrenzt. Zwei reduzierte Wörter können multipliziert werden, indem sie verkettet werden und dann alle Generator-inversen Paare entfernt werden, die sich aus der Verkettung ergeben.

Der Satz von Nielsen-Schreier besagt, dass, wenn H eine Untergruppe einer freien Gruppe G ist , H selbst isomorph zu einer freien Gruppe ist. Das heißt, es existiert eine Menge S von Elementen , die erzeugt H , ohne nicht - triviale Beziehungen zwischen den Elementen S .

Die Nielsen-Schreier-Formel oder Schreier-Index-Formel quantifiziert das Ergebnis für den Fall, dass die Untergruppe einen endlichen Index hat: wenn G eine freie Gruppe vom Rang n (frei auf n Generatoren) und H eine Untergruppe mit endlichem Index ist [ G  : H ] = e , dann ist H rangfrei .

Beispiel

Sei G die freie Gruppe mit zwei Generatoren , und sei H die Untergruppe aller reduzierten Wörter gerader Länge (Produkte einer geraden Anzahl von Buchstaben ). Dann wird H durch seine sechs Elemente erzeugt. Eine Faktorisierung jedes reduzierten Wortes in H in diese Generatoren und ihre Umkehrungen kann einfach konstruiert werden, indem aufeinanderfolgende Buchstabenpaare in dem reduzierten Wort genommen werden. Dies ist jedoch keine freie Präsentation von H, da die letzten drei Generatoren in Bezug auf die ersten drei als geschrieben werden können . H wird vielmehr als freie Gruppe von den drei Elementen erzeugt , die keine Beziehungen untereinander haben; oder stattdessen durch mehrere andere Tripel der sechs Generatoren. Weiterhin ist G auf n = 2 Generatoren frei, H hat den Index e = [ G  : H ] = 2 in G , und H ist auf 1 + e ( n –1) = 3 Generatoren frei. Der Satz von Nielsen-Schreier besagt, dass wie H jede Untergruppe einer freien Gruppe als freie Gruppe erzeugt werden kann, und wenn der Index von H endlich ist, wird sein Rang durch die Indexformel gegeben.

Nachweisen

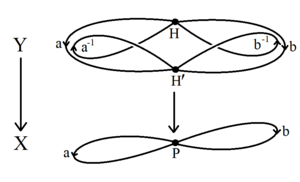
Die freie Gruppe G = π 1 ( X ) hat n = 2 Generatoren zu entsprechenden Schleifen einen , b vom Basispunkt P in X . Die Untergruppe H der Wörter gerader Länge mit dem Index e = [ G  : H ] = 2 entspricht dem überdeckenden Graphen Y mit zwei Knoten entsprechend den Nebenklassen H und H' = aH = bH = a −1 H = b − 1 H , und zwei angehobene Kanten für jede der ursprünglichen Schleifenkanten a , b . Das Kontrahieren einer der Kanten von Y ergibt eine Homotopieäquivalenz zu einem Bouquet von drei Kreisen, so dass H = π 1 ( Y ) eine freie Gruppe auf drei Generatoren ist, zum Beispiel aa , ab , ba .

Ein kurzer Beweis des Nielsen-Schreier-Theorems verwendet die algebraische Topologie von Fundamentalgruppen und überdeckenden Räumen . Eine freie Gruppe G auf einer Menge von Generatoren ist die Fundamentalgruppe eines Bouquets von Kreisen , eines topologischen Graphen X mit einem einzelnen Knoten und mit einer Schleifenkante für jeden Generator. Jede Untergruppe H der Fundamentalgruppe ist selbst die Fundamentalgruppe eines zusammenhängenden überdeckenden Raums Y → X. Der Raum Y ist ein (möglicherweise unendlicher) topologischer Graph, wobei der Schreier-Nebenklassengraph eine Ecke für jede Nebenklasse in G/H hat . In jedem verbundenen topologischen Graphen ist es möglich, die Kanten eines aufspannenden Baums des Graphen zu verkleinern , wodurch ein Kreis von Kreisen erzeugt wird, der dieselbe Fundamentalgruppe H hat . Da H die Grundgruppe eines Kreisstraußes ist, ist es selbst frei.

Die vereinfachte Homologie ermöglicht die Berechnung des Rangs von H , der gleich h 1 ( Y ), der ersten Betti-Zahl des überdeckenden Raums, der Anzahl der unabhängigen Zyklen ist. Für G frei vom Rang n , die Graph X hat n Kanten und Scheitelpunkt 1; vorausgesetzt H hat finite - Index [ G  : H ] = e , das Abdeckmaterial Graph Y hat en Kanten und e Vertices. Die erste Betti-Zahl eines Graphen ist gleich der Anzahl der Kanten minus der Anzahl der Knoten plus der Anzahl der zusammenhängenden Komponenten; daher ist der Rang von H :

Dieser Beweis geht auf Reinhold Bär und Friedrich Levi  ( 1936 ) zurück; der ursprüngliche Beweis von Schreier bildet den Schreier-Graphen auf andere Weise als Quotienten des Cayley-Graphen von G modulo der Wirkung von H .

Nach dem Untergruppenlemma von Schreier kann eine Menge von Generatoren für eine freie Darstellung von H aus Zyklen im überdeckenden Graphen konstruiert werden , die durch Verketten eines aufspannenden Baumpfads von einem Basispunkt (der Nebenklasse der Identität) zu einer der Nebenklassen gebildet werden, a einzelne Nicht-Baum-Kante und ein inverser Spannbaumpfad vom anderen Endpunkt der Kante zurück zum Basispunkt.

Axiomatische Grundlagen

Obwohl mehrere verschiedene Beweise des Nielsen-Schreier-Theorems bekannt sind, hängen sie alle vom Auswahlaxiom ab . Im Beweis, der auf fundamentalen Gruppen von Bouquets basiert, erscheint das Auswahlaxiom beispielsweise in der Gestalt der Aussage, dass jeder zusammenhängende Graph einen aufspannenden Baum besitzt. Die Verwendung dieses Axioms ist notwendig, da es Modelle der Zermelo-Fraenkel-Mengentheorie gibt, in denen sowohl das Auswahlaxiom als auch der Nielsen-Schreier-Satz falsch sind. Der Satz von Nielsen-Schreier wiederum impliziert eine schwächere Version des Auswahlaxioms für endliche Mengen.

Geschichte

Der Satz von Nielsen-Schreier ist ein nicht-abelsches Analogon eines älteren Ergebnisses von Richard Dedekind , dass jede Untergruppe einer freien abelschen Gruppe frei abelsch ist .

Jakob Nielsen ( 1921 ) bewies ursprünglich eine eingeschränkte Form des Theorems, der besagt, dass jede endlich erzeugte Untergruppe einer freien Gruppe frei ist. Sein Beweis beinhaltet die Durchführung einer Folge von Nielsen-Transformationen an der Erzeugungsmenge der Untergruppe, die ihre Länge reduzieren (als reduzierte Wörter in der freien Gruppe, aus der sie gezogen werden). Otto Schreier bewies den Nielsen-Schreier Satz in seiner vollen Allgemeinheit in seiner 1926 Habilitation Dissertation , Die Untergruppen der Freien Gruppe , auch im Jahr 1927 in der veröffentlichten Abh. Mathematik. Sem. Hamburg. Univ.

Der topologische Beweis anhand fundamentaler Kreissträuße geht auf Reinhold Baer und Friedrich Levi  ( 1936 ) zurück. Ein weiterer topologischer Beweis, basierend auf der Bass-Serre-Theorie der Gruppenwirkungen auf Bäumen , wurde von Jean-Pierre Serre  ( 1970 ) veröffentlicht.

Siehe auch

Anmerkungen

Verweise