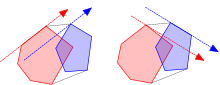
Rotierende Bremssättel - Rotating calipers

Sequenz von Sonden um die konvexe Hülle eines Polygons, um seinen Durchmesser unter Verwendung der Rotating Caliper-Methode zu bestimmen.

In der Computergeometrie ist das Verfahren zum Drehen von Bremssätteln eine Algorithmusentwurfstechnik , die verwendet werden kann, um Optimierungsprobleme zu lösen, einschließlich des Ermittelns der Breite oder des Durchmessers eines Satzes von Punkten.

Die Methode wird so genannt, weil die Idee analog zum Drehen eines federbelasteten Messschiebers um die Außenseite eines konvexen Polygons ist . Jedes Mal, wenn eine Klinge des Bremssattels flach an einer Kante des Polygons anliegt, bildet sie ein antipodales Paar, wobei die Spitze oder Kante die gegenüberliegende Klinge berührt. Die vollständige "Drehung" des Bremssattels um das Polygon erkennt alle antipodalen Paare; Die Menge aller Paare, die als Grafik betrachtet wird, bildet einen Knackpunkt . Das Verfahren zum Drehen von Bremssätteln kann als das projektive Dual eines Sweep-Linien-Algorithmus interpretiert werden, bei dem der Sweep über Steigungen von Linien und nicht über x- oder y- Koordinaten von Punkten erfolgt.

Geschichte

Ein antipodales Scheitelpunktpaar und ihre unterstützenden parallelen Linien .

Die Methode der rotierenden Bremssättel wurde erstmals 1978 in der Dissertation von Michael Shamos verwendet . Shamos verwendet diese Methode, um alle antipodalen Punktpaare auf einem konvexen Polygon zu erzeugen und den Durchmesser eines konvexen Polygons zeitlich zu berechnen . Godfried Toussaint prägte den Ausdruck "rotierende Bremssättel" und demonstrierte auch, dass die Methode zur Lösung vieler anderer Probleme mit der rechnerischen Geometrie anwendbar ist. ${\ displaystyle O (n)}$

Rotierende Bremssättel, die eine Brücke zwischen zwei konvexen Polygonen finden

Shamos 'Algorithmus

Shamos gab in seiner Dissertation (S. 77–82) folgenden Algorithmus für die Methode der rotierenden Bremssättel an, mit der alle antipodalen Eckpunktpaare auf einem konvexen Polygon erzeugt wurden:

/* p[] is in standard form, ie, counter clockwise order, 
     distinct vertices, no collinear vertices.
   ANGLE(m, n) is a procedure that returns the clockwise angle 
     swept out by a ray as it rotates from a position parallel 
     to the directed segment Pm,Pm+1 to a position parallel to Pn, Pn+1
   We assume all indices are reduced to mod N (so that N+1 = 1).
*/
GetAllAntiPodalPairs(p[1..n])
    // Find first anti-podal pair by locating vertex opposite P1
    i = 1
    j = 2
    while angle(i, j) < pi
        j++
    yield i, j

    /* Now proceed around the polygon taking account of
         possibly parallel edges. Line L passes through
         Pi, Pi+1 and M passes through Pj, Pj+1
    */

    // Loop on j until all of P has been scanned
    current = i    
    while j != n
        if angle(current, i + 1) <= angle(current, j + 1)
            j++
            current = j
        else
            i++
            current = i
        yield i, j

        // Now take care of parallel edges
        if angle(current, i + 1) = angle(current, j + 1)
            yield i + 1, j
            yield i, j + 1
            yield i + 1, j + 1
            if current = i
                j++
            else
                i++

Eine andere Version dieses Algorithmus erschien 1985 im Text von Preparata und Shamos, bei der die Berechnung von Winkeln vermieden wurde:

GetAllAntiPodalPairs(p[1..n])
    i0 = n
    i = 1
    j = i + 1
    while (Area(i, i + 1, j + 1) > Area(i, i + 1, j))
        j = j + 1
        j0 = j
    while (j != i0)
        i = i + 1
        yield i, j
        while (Area(i, i + 1, j + 1) > Area(i, i + 1, j)
            j = j + 1
            if ((i, j) != (j0, i0))
                yield i, j
            else 
                return
        if (Area(j, i + 1, j + 1) = Area(i, i + 1, j))
            if ((i, j) != (j0, i0))
                yield i, j + 1
            else 
                yield i + 1, j

Anwendungen

Pirzadeh beschreibt verschiedene Anwendungen der Methode der rotierenden Bremssättel.

Entfernungen

• Durchmesser (maximale Breite) eines konvexen Polygons
• Breite ( Mindestbreite ) eines konvexen Polygons
• Maximaler Abstand zwischen zwei konvexen Polygonen
• Mindestabstand zwischen zwei konvexen Polygonen
• Breitester leerer (oder trennender) Streifen zwischen zwei konvexen Polygonen (eine vereinfachte niedrigdimensionale Variante eines Problems, das beim maschinenbasierten maschinellen Lernen von Unterstützungsvektoren auftritt )
• Grenanderabstand zwischen zwei konvexen Polygonen
• Optimale Streifentrennung (zur medizinischen Bildgebung und Festkörpermodellierung)

Begrenzungsrahmen

• Minimaler flächenorientierter Begrenzungsrahmen
• Minimaler Umfang orientierter Begrenzungsrahmen

Triangulationen

• Zwiebel- Triangulationen
• Spiral Triangulation
• Viereck
• Schöne Triangulation
• Kunstgalerie Problem
• Problem bei der Optimierung der Keilplatzierung

Multi-Polygon-Operationen

• Vereinigung zweier konvexer Polygone
• Gemeinsame Tangenten an zwei konvexe Polygone
• Schnittpunkt zweier konvexer Polygone
• Kritische Stützlinien zweier konvexer Polygone
• Vektorsummen (oder Minkowski-Summe) zweier konvexer Polygone
• Konvexe Hülle aus zwei konvexen Polygonen

Durchquerungen

• Kürzeste Transversale
• Dünnstreifen-Transversale

Andere

• Nichtparametrische Entscheidungsregeln für die maschinell erlernte Klassifizierung
• Öffnungswinkeloptimierungen für Sichtbarkeitsprobleme in der Computersicht
• Suche nach längsten Zellen in Millionen von biologischen Zellen
• Vergleich der Präzision von zwei Personen am Schießstand
• Klassifizieren Sie Gehirnabschnitte anhand von Scanbildern

Siehe auch

• Konvexes Polygon
• Konvexer Rumpf
• Kleinste beiliegende Box

Verweise