Skalares Potenzial - Scalar potential

Skalarpotential , einfach ausgedrückt, beschreibt die Situation, in der die Differenz der potentiellen Energien eines Objekts an zwei verschiedenen Positionen nur von den Positionen abhängt, nicht von dem Weg, den das Objekt bei der Bewegung von einer Position zur anderen nimmt. Es ist ein Skalarfeld im Dreiraum: ein richtungsloser Wert (Skalar), der nur von seiner Lage abhängt. Ein bekanntes Beispiel ist die potentielle Energie aufgrund der Schwerkraft.

Gravitationspotentialtopf mit zunehmender Masse, wobei ${\displaystyle \mathbf{F} =-\nabla P}$

Eine skalare Potential ist ein grundlegendes Konzept in Vektoranalyse und Physik (das Adjektiv Skalar häufig weggelassen wird , wenn es keine Gefahr der Verwechslung mit ist Vektorpotential ). Das Skalarpotential ist ein Beispiel für ein Skalarfeld . Bei einem Vektorfeld F ist das Skalarpotential P so definiert, dass:

${\displaystyle \mathbf{F} =-\nabla P=-\left({\frac {\partial P}{\partial x}},{\frac {\partial P}{\partial y}},{\ frac {\partial P}{\partial z}}\right),}$

wobei ∇ P der Gradient von P ist und der zweite Teil der Gleichung minus dem Gradienten für eine Funktion der kartesischen Koordinaten x , y , z ist . In einigen Fällen können Mathematiker ein positives Vorzeichen vor dem Gradienten verwenden, um das Potenzial zu definieren. Aufgrund dieser Definition von P in Bezug auf den Gradienten ist die Richtung von F an jedem Punkt die Richtung der steilsten Abnahme von P an diesem Punkt, ihre Größe ist die Rate dieser Abnahme pro Längeneinheit.

Damit F nur durch ein skalares Potential beschrieben werden kann, muss eine der folgenden äquivalenten Aussagen wahr sein:

1. ${\displaystyle -\int_{a}^{b}\mathbf {F} \cdot d\mathbf {l} =P(\mathbf{b})-P(\mathbf{a})}$, wobei die Integration über einen Jordanbogen erfolgt , der von Ort a zu Ort b verläuft und P ( b ) P am Ort b ausgewertet wird .
2. ${\displaystyle \oint\mathbf{F}\cdot d\mathbf{l} =0}$, wobei das Integral über einem einfachen geschlossenen Pfad liegt, der auch als Jordan-Kurve bekannt ist .
3. ${\displaystyle {\nabla}\times {\mathbf{F}}=0.}$

Die erste dieser Bedingungen stellt den fundamentalen Satz des Gradienten dar und gilt für jedes Vektorfeld, das ein Gradient eines differenzierbaren einwertigen Skalarfeldes P ist . Die zweite Bedingung ist eine Anforderung an F, damit sie als Gradient einer Skalarfunktion ausgedrückt werden kann. Die dritte Bedingung drückt die zweite Bedingung in Bezug auf die Locke von F unter Verwendung des Fundamentalsatzes der Locke erneut aus . Ein Vektorfeld F , das diese Bedingungen erfüllt, heißt drehungsfrei (konservativ).

Skalare Potentiale spielen in vielen Bereichen der Physik und der Ingenieurwissenschaften eine herausragende Rolle. Das Gravitationspotential ist das mit der Gravitation pro Masseneinheit verbundene skalare Potential, dh die Beschleunigung aufgrund des Feldes, als Funktion der Position. Das Gravitationspotential ist die potentielle Gravitationsenergie pro Masseneinheit. In der Elektrostatik ist das elektrische Potential das mit dem elektrischen Feld verbundene Skalarpotential , dh die elektrostatische Kraft pro Ladungseinheit . Das elektrische Potential ist in diesem Fall die elektrostatische potentielle Energie pro Ladungseinheit. In der Fluiddynamik haben rotationsfreie Lamellenfelder nur im Sonderfall ein skalares Potential, wenn es sich um ein Laplace-Feld handelt . Bestimmte Aspekte der Kernkraft können durch ein Yukawa-Potential beschrieben werden . Das Potential spielt in den Lagrange- und Hamilton- Formulierungen der klassischen Mechanik eine herausragende Rolle . Außerdem ist das Skalarpotential die fundamentale Größe in der Quantenmechanik .

Nicht jedes Vektorfeld hat ein skalares Potential. Diejenigen, die dies tun, werden konservativ genannt , entsprechend dem Begriff der konservativen Kraft in der Physik. Beispiele für nichtkonservative Kräfte umfassen Reibungskräfte, magnetische Kräfte und in der Strömungsmechanik ein elektromagnetisches Feldgeschwindigkeitsfeld. Nach dem Helmholtz-Zerlegungssatz können jedoch alle Vektorfelder durch ein skalares Potential und ein entsprechendes Vektorpotential beschrieben werden . In der Elektrodynamik werden das elektromagnetische Skalar- und Vektorpotential zusammen als elektromagnetisches Viererpotential bezeichnet .

Integrierbarkeitsbedingungen

Wenn F a ist konservative Vektorfeld (auch genannt irrotational , curl -freien oder Potential ) und deren Einzelteile kontinuierlichen partiellen Ableitungen , das Potential von F in bezug auf einen Bezugspunkt in Bezug auf die definierten Linienintegral : ${\displaystyle \mathbf {r} _{0}}$

${\displaystyle V(\mathbf{r})=-\int_{C}\mathbf{F} (\mathbf{r})\cdot\,d\mathbf{r} =-\int_{a}^ {b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt,}$

wobei C ein parametrisierter Pfad von nach . ist${\displaystyle \mathbf {r} _{0}}$${\displaystyle\mathbf{r},}$

${\displaystyle \mathbf {r} (t),a\leq t\leq b,\mathbf {r} (a)=\mathbf {r_{0}} ,\mathbf {r} (b)=\mathbf { r} .}$

Die Tatsache, dass das Geradenintegral nur durch seine Endpunkte vom Weg C abhängt und im Wesentlichen die Wegunabhängigkeitseigenschaft eines konservativen Vektorfeldes ist. Der fundamentale Satz der Linienintegrale besagt, dass, wenn V auf diese Weise definiert ist , V ein skalares Potential des konservativen Vektorfeldes F ist . Das skalare Potential wird nicht allein durch das Vektorfeld bestimmt: Tatsächlich wird der Gradient einer Funktion nicht beeinflusst, wenn eine Konstante dazu addiert wird. Wird V durch das Linienintegral definiert, spiegelt die Mehrdeutigkeit von V die Freiheit bei der Wahl des Bezugspunktes${\displaystyle \mathbf {r} _{0}}$${\displaystyle\mathbf{r}}$${\displaystyle \mathbf{F} =-\nabla V,}$${\displaystyle \mathbf {r} _{0}.}$

Höhe als potentielle Gravitationsenergie

gleichmäßiges Gravitationsfeld nahe der Erdoberfläche

Plot einer zweidimensionalen Schicht des Gravitationspotentials in und um einen gleichförmigen kugelförmigen Körper. Die Wendepunkte des Querschnitts liegen an der Körperoberfläche.

Ein Beispiel ist das (fast) gleichförmige Gravitationsfeld nahe der Erdoberfläche. Es hat eine potentielle Energie

${\displaystyle U=mgh}$

wobei U die potentielle Gravitationsenergie und h die Höhe über der Oberfläche ist. Dies bedeutet , dass potentielle Energie auf einer Konturkarte ist auf Höhe proportional. Auf einer Konturkarte ist der zweidimensionale negative Gradient der Höhe ein zweidimensionales Vektorfeld, dessen Vektoren immer senkrecht zu den Konturen und auch senkrecht zur Schwerkraftrichtung stehen. Aber auf der hügeligen Region, die durch die Höhenlinienkarte repräsentiert wird, zeigt der dreidimensionale negative Gradient von U immer gerade nach unten in Richtung der Schwerkraft; F . Ein Ball, der einen Hügel hinunterrollt, kann sich jedoch aufgrund der Normalkraft der Hügeloberfläche nicht direkt nach unten bewegen , die die Schwerkraftkomponente senkrecht zur Hügeloberfläche aufhebt. Die zur Bewegung des Balls verbleibende Schwerkraftkomponente ist parallel zur Oberfläche:

${\displaystyle F_{S}=-mg\\sin\theta}$

wobei θ der Neigungswinkel ist und die Komponente von F _S senkrecht zur Schwerkraft ist

${\displaystyle F_{P}=-mg\\sin\theta\\cos\theta=-{1\over 2}mg\sin 2\theta.}$

Diese Kraft F _P parallel zum Boden ist am größten, wenn θ 45 Grad beträgt.

Sei Δ h das einheitliche Höhenintervall zwischen Konturen auf der Konturkarte und sei Δ x der Abstand zwischen zwei Konturen. Dann

${\displaystyle \theta =\tan^{-1}{\frac {\Updelta h}{\Updelta x}}}$

so dass

${\displaystyle F_{P}=-mg{\Updelta x\,\Updelta h\over \Updelta x^{2}+\Updelta h^{2}}.}$

Auf einer Konturkarte ist der Gradient jedoch umgekehrt proportional zu Δ x , was der Kraft F _P nicht ähnlich ist : Die Höhe auf einer Konturkarte ist nicht genau ein zweidimensionales Potentialfeld. Die Stärke der Kräfte ist unterschiedlich, aber die Richtungen der Kräfte sind auf einer Höhenlinienkarte sowie auf der hügeligen Region der Erdoberfläche, die durch die Höhenlinienkarte dargestellt wird, gleich.

Druck als Auftriebspotential

In der Strömungsmechanik wird eine Flüssigkeit im Gleichgewicht, aber bei Vorhandensein eines gleichmäßigen Gravitationsfeldes von einer gleichmäßigen Auftriebskraft durchdrungen, die die Gravitationskraft aufhebt: So hält die Flüssigkeit ihr Gleichgewicht. Diese Auftriebskraft wird der negativer Gradient des Drucks :

${\displaystyle \mathbf{f_{B}} =-\nabla p.\,}$

Da der Auftrieb entgegen der Schwerkraft nach oben zeigt, steigt der Druck in der Flüssigkeit nach unten. Der Druck in einem ruhenden Gewässer nimmt proportional zur Tiefe unter der Wasseroberfläche zu. Die Flächen konstanten Drucks sind zur Fläche parallele Ebenen, die als Nulldruckebene bezeichnet werden können.

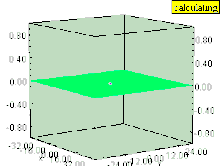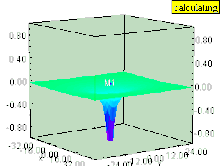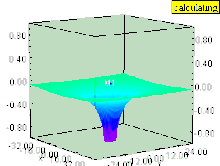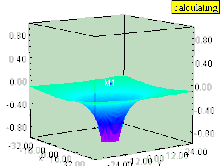
Hat die Flüssigkeit einen vertikalen Wirbel (dessen Rotationsachse senkrecht zur Oberfläche steht), dann verursacht der Wirbel eine Depression im Druckfeld. Die Flüssigkeitsoberfläche innerhalb des Wirbels wird nach unten gezogen, ebenso wie alle Flächen gleichen Drucks, die noch parallel zur Flüssigkeitsoberfläche bleiben. Der Effekt ist innerhalb des Wirbels am stärksten und nimmt mit dem Abstand von der Wirbelachse schnell ab.

Die Auftriebskraft einer Flüssigkeit auf einen festen Gegenstand, der von dieser Flüssigkeit eingetaucht und umgeben ist, kann durch Integration des negativen Druckgradienten entlang der Oberfläche des Gegenstands ermittelt werden:

${\displaystyle F_{B}=-\oint_{S}\nabla p\cdot \,d\mathbf{S} .}$

Skalares Potential im euklidischen Raum

Im 3-dimensionalen euklidischen Raum ist das Skalarpotential eines drehungsfreien Vektorfeldes E gegeben durch ${\displaystyle \mathbb{R} ^{3}}$

${\displaystyle \Phi (\mathbf {r} )={1 \over 4\pi}\int _{\mathbb {R} ^{3}}{\frac {\operatorname {div} \mathbf {E} ( \mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|}}\,dV(\mathbf {r} ')}$

wobei ein infinitesimales Volumenelement bezüglich r' ist . Dann ${\displaystyle dV(\mathbf{r}')}$

${\displaystyle \mathbf {E} =-\mathbf {\nabla} \Phi =-{1 \over 4\pi}\mathbf {\nabla} \int _{\mathbb {R} ^{3}}{\ frac {\operatorname {div} \mathbf {E} (\mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|}}\,dV(\mathbf {r} ' )}$

Dies gilt, vorausgesetzt, E ist stetig und verschwindet asymptotisch gegen Null, wobei es schneller als 1/ r abfällt, und wenn die Divergenz von E ebenfalls gegen Unendlich verschwindet, zerfällt es schneller als 1/ r ² .

Anders geschrieben, lass

${\displaystyle \Gamma(\mathbf{r})={\frac{1}{4\pi}}{\frac{1}{\|\mathbf{r}\|}}}$

sei das Newtonsche Potential . Dies ist die grundlegende Lösung der Laplace-Gleichung , was bedeutet, dass der Laplace-Operator von Γ gleich dem Negativen der Dirac-Deltafunktion ist :

${\displaystyle \nabla^{2}\Gamma (\mathbf{r})+\delta (\mathbf{r})=0.}$

Dann ist das Skalarpotential die Divergenz der Faltung von E mit Γ :

${\displaystyle \Phi =\operatorname {div} (\mathbf {E} *\Gamma).}$

Tatsächlich ist die Faltung eines drehungsfreien Vektorfeldes mit einem rotationsinvarianten Potential auch drehungsfrei. Für ein drehungsfreies Vektorfeld G kann gezeigt werden, dass

${\displaystyle \nabla^{2}\mathbf {G} =\mathbf {\nabla} (\mathbf {\nabla} \cdot {}\mathbf {G}).}$

Daher

${\displaystyle \nabla \operatorname {div} (\mathbf {E} *\Gamma )=\nabla ^{2}(\mathbf {E} *\Gamma )=\mathbf {E} *\nabla ^{2} \Gamma =-\mathbf{E} *\delta =-\mathbf{E}}$

nach Bedarf.

Allgemeiner ausgedrückt ist die Formel

${\displaystyle \Phi =\operatorname {div} (\mathbf {E} *\Gamma )}$

gilt im n- dimensionalen euklidischen Raum ( n > 2 ) mit dem Newtonschen Potential dann gegeben durch

${\displaystyle \Gamma(\mathbf{r})={\frac{1}{n(n-2)\omega_{n}\|\mathbf{r}\|^{n-2}}}}$

wobei ω _n das Volumen der Einheit n -Kugel ist. Der Beweis ist identisch. Alternativ liefert die partielle Integration (oder genauer gesagt die Eigenschaften der Faltung )

${\displaystyle \Phi(\mathbf{r})=-{\frac{1}{n\omega_{n}}}\int_{\mathbb{R}^{n}}{\frac{\mathbf {E} (\mathbf {r} ')\cdot (\mathbf {r} -\mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|^{n}} }\,dV(\mathbf{r}').}$

Siehe auch

• Gradientensatz
• Fundamentaler Satz der Vektoranalyse
• Äquipotential- (Isopotential-)Linien und -Flächen

Verweise