Symmetrie (Geometrie) - Symmetry (geometry)

In der Geometrie hat ein Objekt Symmetrie, wenn es eine Operation oder Transformation (wie Translation , Skalierung , Rotation oder Reflexion ) gibt, die die Figur / das Objekt auf sich selbst abbildet (dh das Objekt hat eine Invarianz unter der Transformation). Eine Symmetrie kann daher als Immunität gegen Veränderungen angesehen werden. Beispielsweise hat ein Kreis, der um seinen Mittelpunkt gedreht wird, dieselbe Form und Größe wie der ursprüngliche Kreis, da alle Punkte vor und nach der Transformation nicht zu unterscheiden wären. Ein Kreis soll also unter Rotation symmetrisch sein oder Rotationssymmetrie haben . Wenn die Isometrie die Reflexion einer ebenen Figur um eine Linie ist, wird die Figur als Reflexionssymmetrie oder Liniensymmetrie bezeichnet ; Es ist auch möglich, dass eine Figur / ein Objekt mehr als eine Symmetrielinie aufweist.
Welche Arten von Symmetrien für ein geometrisches Objekt möglich sind, hängt von der Menge der verfügbaren geometrischen Transformationen ab und davon, welche Objekteigenschaften nach einer Transformation unverändert bleiben sollen. Da die Zusammensetzung zweier Transformationen auch eine Transformation ist und jede Transformation per Definition eine inverse Transformation aufweist, die sie rückgängig macht, bildet die Menge der Transformationen, unter denen ein Objekt symmetrisch ist, eine mathematische Gruppe , die Symmetriegruppe des Objekts.
Euklidische Symmetrien im Allgemeinen
Die häufigste Gruppe von Transformationen, die auf Objekte angewendet werden, wird als euklidische Gruppe von " Isometrien " bezeichnet. Hierbei handelt es sich um abstandserhaltende Transformationen im Raum, die üblicherweise als zweidimensional oder dreidimensional bezeichnet werden (dh in Ebenengeometrie oder euklidischen Räumen mit fester Geometrie ). . Diese Isometrien bestehen aus Reflexionen , Rotationen , Translationen und Kombinationen dieser Grundoperationen. Bei einer isometrischen Transformation wird ein geometrisches Objekt als symmetrisch bezeichnet, wenn das Objekt nach der Transformation vor der Transformation nicht vom Objekt zu unterscheiden ist. Ein geometrisches Objekt ist typischerweise nur unter einer Teilmenge oder " Untergruppe " aller Isometrien symmetrisch . Die Arten von Isometrie-Untergruppen werden nachstehend beschrieben, gefolgt von anderen Arten von Transformationsgruppen und von den Arten der Objektinvarianz, die in der Geometrie möglich sind.
Nach dem Cartan-Dieudonné-Theorem kann eine orthogonale Transformation im n- dimensionalen Raum durch die Zusammensetzung von höchstens n Reflexionen dargestellt werden.
| 1D | 2D | 3D | 4D | |||||
| Reflexionen | Punkt | Affine | Punkt | Affine | Punkt | Affine | Punkt | Affine |
|---|---|---|---|---|---|---|---|---|
| 1 | Reflexion | Reflexion | Reflexion | Reflexion | ||||
| 2 | Übersetzung | Drehung | Übersetzung | Drehung | Übersetzung | Drehung | Übersetzung | |
| 3 | Transflektion | Rotoreflexion | Transflektion | Rotoreflexion | Transflektion | |||
| 4 | Rotary Übersetzung | Doppelte Drehung | Rotary Übersetzung | |||||
| 5 | Rotationstransflexion | |||||||
Reflexionssymmetrie
Reflexionssymmetrie, lineare Symmetrie, Spiegelsymmetrie, Spiegelbildsymmetrie oder bilaterale Symmetrie ist Symmetrie in Bezug auf Reflexion.
In einer Dimension gibt es einen Symmetriepunkt, an dem Reflexion stattfindet; In zwei Dimensionen gibt es eine Symmetrieachse (auch bekannt als Symmetrielinie), und in drei Dimensionen gibt es eine Symmetrieebene. Ein Objekt oder eine Figur, für die jeder Punkt eine Eins-zu-Eins-Abbildung auf einen anderen hat, der von und auf gegenüberliegenden Seiten einer gemeinsamen Ebene gleich weit entfernt ist, wird als spiegelsymmetrisch bezeichnet (weitere Informationen finden Sie unter Spiegelbild ).
Die Symmetrieachse einer zweidimensionalen Figur ist eine Linie, so dass bei der Konstruktion einer Senkrechten zwei beliebige Punkte, die in gleichen Abständen von der Symmetrieachse auf der Senkrechten liegen, identisch sind. Eine andere Möglichkeit, darüber nachzudenken, besteht darin, dass, wenn die Form über die Achse in zwei Hälften gefaltet würde, die beiden Hälften als Spiegelbilder voneinander identisch wären. Beispielsweise. Ein Quadrat hat vier Symmetrieachsen, da es vier verschiedene Möglichkeiten gibt, es zu falten und die Kanten aufeinander abzustimmen. Ein anderes Beispiel wäre das eines Kreises , dessen Mittelpunkt aus demselben Grund unendlich viele Symmetrieachsen durchläuft.
Wenn der Buchstabe T entlang einer vertikalen Achse reflektiert wird, erscheint er gleich. Dies wird manchmal als vertikale Symmetrie bezeichnet. Somit kann man dieses Phänomen eindeutig beschreiben, indem man sagt, dass "T eine vertikale Symmetrieachse hat" oder dass "T eine Links-Rechts-Symmetrie hat".
Die Dreiecke mit Reflexionssymmetrie sind gleichschenklig , die Vierecke mit dieser Symmetrie sind Drachen und gleichschenklige Trapezoide .
Für jede Linie oder Ebene der Reflexion, die Symmetriegruppe ist isomorph mit C s (siehe Punktgruppen in drei Dimensionen für mehr), einen der drei Typen von um zwei ( Involutionen ), folglich algebraisch isomorph zu C 2 . Die grundlegende Domäne ist eine halbe Ebene oder ein halber Raum .
Punktreflexion und andere involutive Isometrien
Die Reflexionssymmetrie kann auf andere Isometrien des m- dimensionalen Raums verallgemeinert werden, bei denen es sich um Involutionen handelt , wie z
- ( x 1 , ..., x m ) ↦ (- x 1 , ..., - x k , x k + 1 , ..., x m )
in einem bestimmten System kartesischer Koordinaten . Dies spiegelt den Raum entlang eines ( m - k ) -dimensionalen affinen Unterraums wider . Wenn k = m ist , ist eine solche Transformation als Punktreflexion oder Inversion durch einen Punkt bekannt . In der Ebene ( m = 2) entspricht eine Punktreflexion einer halben Umdrehung (180 °). siehe unten. Antipodale Symmetrie ist ein alternativer Name für eine Punktreflexionssymmetrie durch den Ursprung.
Eine solche "Reflexion" bewahrt die Orientierung genau dann, wenn k eine gerade Zahl ist. Dies impliziert, dass für m = 3 (wie auch für andere ungerade m ) eine Punktreflexion die Ausrichtung des Raums wie eine Spiegelbildsymmetrie ändert. Dies erklärt, warum in der Physik der Begriff P- Symmetrie (P steht für Parität ) sowohl für Punktreflexion als auch für Spiegelsymmetrie verwendet wird. Da eine dreidimensionale Punktreflexion ein linkshändiges Koordinatensystem in ein rechtshändiges Koordinatensystem umwandelt , wird die Symmetrie unter einer Punktreflexion auch als Links-Rechts-Symmetrie bezeichnet.
Rotationssymmetrie

Rotationssymmetrie ist Symmetrie in Bezug auf einige oder alle Rotationen im m- dimensionalen euklidischen Raum. Rotationen sind direkte Isometrien , dh Isometrien , die die Orientierung bewahren . Daher ist eine Symmetriegruppe der Rotationssymmetrie eine Untergruppe der speziellen euklidischen Gruppe E + ( m ) .
Symmetrie in Bezug auf alle Rotationen um alle Punkte impliziert Translationssymmetrie in Bezug auf alle Übersetzungen (da Übersetzungen Zusammensetzungen von Rotationen um bestimmte Punkte sind), und die Symmetriegruppe ist das gesamte E + ( m ). Dies gilt nicht für Objekte, da es den Raum homogen macht, kann jedoch für physikalische Gesetze gelten.
Für die Symmetrie in Bezug auf Rotationen um einen Punkt kann man diesen Punkt als Ursprung nehmen. Diese Rotationen bilden die spezielle orthogonale Gruppe SO ( m ), die durch die Gruppe von m × m orthogonalen Matrizen mit Determinante 1 dargestellt werden kann. Für m = 3 ist dies die Rotationsgruppe SO (3) .
Etwas anders formuliert ist die Rotationsgruppe eines Objekts die Symmetriegruppe innerhalb von E + ( m ), der Gruppe starrer Bewegungen; das heißt, der Schnittpunkt der vollständigen Symmetriegruppe und der Gruppe der starren Bewegungen. Für chirale Objekte entspricht dies der vollständigen Symmetriegruppe.
Gesetze der Physik sind SO (3) -invariant, wenn sie keine unterschiedlichen Richtungen im Raum unterscheiden. Wegen Noethers Theorems , Rotationssymmetrie eines physikalischen Systems entspricht den Drehimpulserhaltungssatz . Weitere Informationen finden Sie unter Rotationsinvarianz .
Translationale Symmetrie
Durch die Translationssymmetrie bleibt ein Objekt unter einer diskreten oder kontinuierlichen Gruppe von Übersetzungen unveränderlich . Die Abbildung rechts zeigt vier kongruente Dreiecke, die durch Übersetzungen entlang des Pfeils erzeugt wurden. Wenn sich die Dreieckslinie in beide Richtungen bis ins Unendliche erstrecken würde, hätten sie eine diskrete Translationssymmetrie; Bei jeder Übersetzung, bei der ein Dreieck auf ein anderes abgebildet wird, bleibt die gesamte Zeile unverändert.
Gleitreflexionssymmetrie

In 2D bedeutet eine Gleitreflexionssymmetrie ( in 3D auch als Gleitebenensymmetrie und im Allgemeinen als Transflektion bezeichnet ), dass eine Reflexion in einer Linie oder Ebene in Kombination mit einer Translation entlang der Linie oder in der Ebene zu demselben Objekt führt ( wie im Fall von Fußabdrücken). Die Zusammensetzung von zwei Gleitreflexionen führt zu einer Translationssymmetrie mit dem doppelten Translationsvektor. Die Symmetrie Gruppe umfassend Gleitspiegelung und zugehörige Übersetzungen ist die Fries - Gruppe P11g und isomorph mit der unendlichen zyklischen Gruppe Z .
Rotoreflexionssymmetrie
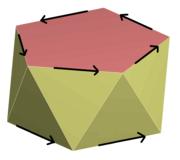
In 3D ist eine Rotationsreflexion , Rotoreflexion oder falsche Drehung eine Rotation um eine Achse, kombiniert mit einer Reflexion in einer Ebene senkrecht zu dieser Achse. Die mit Rotoreflexionen verbundenen Symmetriegruppen umfassen:
- Wenn der Drehwinkel keinen gemeinsamen Teiler mit 360 ° hat, ist die Symmetriegruppe nicht diskret.
- Wenn die Rotoreflexion einen 2 n- fachen Rotationswinkel (Winkel von 180 ° / n ) hat, ist die Symmetriegruppe S 2 n der Ordnung 2 n (nicht zu verwechseln mit symmetrischen Gruppen , für die dieselbe Notation verwendet wird; die Zusammenfassung Gruppe ist C 2n ). Ein Sonderfall ist n = 1, eine Inversion , da sie nicht von der Achse und der Ebene abhängt. Es ist nur durch den Umkehrpunkt gekennzeichnet.
- Die Gruppe C nh (Winkel von 360 ° / n ); für ungerade n wird dies durch eine einzelne Symmetrie erzeugt, und die abstrakte Gruppe ist C 2 n , für gerade n . Dies ist keine grundlegende Symmetrie, sondern eine Kombination.
Weitere Informationen finden Sie unter Punktgruppen in drei Dimensionen .
Helixsymmetrie
In der 3D-Geometrie und höher ist eine Schraubenachse (oder Rotationsverschiebung) eine Kombination aus einer Drehung und einer Verschiebung entlang der Drehachse.
Helixsymmetrie ist die Art von Symmetrie, die in Alltagsgegenständen wie Federn , Slinky- Spielzeugen, Bohrern und Schnecken zu sehen ist . Das Konzept der helikalen Symmetrie kann als die Verfolgung im dreidimensionalen Raum visualisiert werden, die sich aus der Drehung eines Objekts mit einer konstanten Winkelgeschwindigkeit ergibt , während gleichzeitig mit einer konstanten linearen Geschwindigkeit entlang seiner Drehachse verschoben wird. Zu jedem Zeitpunkt ergeben diese beiden Bewegungen zusammen einen Wickelwinkel , mit dessen Hilfe die Eigenschaften der verfolgten Helix definiert werden können. Wenn sich das Verfolgungsobjekt schnell dreht und langsam verschiebt, liegt der Aufwickelwinkel nahe bei 0 °. Wenn sich das Objekt dagegen langsam dreht und sich schnell verschiebt, nähert sich der Aufwickelwinkel 90 °.
Basierend auf dem Zusammenspiel des Wickelwinkels und der Translationssymmetrien entlang der Achse können drei Hauptklassen der Helixsymmetrie unterschieden werden:


- Unendliche helikale Symmetrie : Wenn es keine Unterscheidungsmerkmale entlang der Länge einer Helix oder eines helixartigen Objekts gibt, hat das Objekt eine unendliche Symmetrie ähnlich der eines Kreises, jedoch mit der zusätzlichen Anforderung der Translation entlang der Längsachse des Objekts. um es wieder in sein ursprüngliches Aussehen zu versetzen. Ein helixartiges Objekt ist eines, das an jedem Punkt den regelmäßigen Aufwickelwinkel einer Helix hat, aber auch einen unendlich hohen Querschnitt haben kann , vorausgesetzt, dass genau derselbe Querschnitt (normalerweise nach einer Drehung) bei existiert jeder Punkt entlang der Länge des Objekts. Einfache Beispiele sind gleichmäßig gewickelte Federn, Slinkies, Bohrer und Schnecken. Genauer gesagt hat ein Objekt unendliche helikale Symmetrien, wenn für eine kleine Drehung des Objekts um seine Mittelachse ein Punkt in der Nähe (der Translationsabstand) auf dieser Achse vorhanden ist, an dem das Objekt genau wie zuvor erscheint. Es ist diese unendliche helikale Symmetrie, die die merkwürdige Illusion einer Bewegung entlang der Länge einer Schnecke oder eines Schraubenbohrers hervorruft, die gedreht werden. Es bietet auch die mechanisch nützliche Fähigkeit solcher Vorrichtungen, Materialien entlang ihrer Länge zu bewegen, vorausgesetzt, sie sind mit einer Kraft wie Schwerkraft oder Reibung kombiniert, die es den Materialien ermöglicht, sich einer einfachen Rotation mit dem Bohrer oder der Schnecke zu widersetzen.
- n- fache Helixsymmetrie : Wenn die Anforderung, dass jeder Querschnitt des Helixobjekts identisch sein muss, gelockert wird, werden zusätzliche geringere Helixsymmetrien möglich. Beispielsweise kann sich der Querschnitt des Helixobjekts ändern, sich jedoch immer noch regelmäßig entlang der Achse des Helixobjekts wiederholen. Folglich weisen Objekte dieses Typs nach einer Drehung um einen festen Winkel & thgr; und einer Verschiebung um einen festen Abstand eine Symmetrie auf, sind jedoch im Allgemeinen für keinen Drehwinkel unveränderlich. Wenn sich der Drehwinkel, unter dem die Symmetrie auftritt, gleichmäßig in einen vollen Kreis (360 °) teilt, ist das Ergebnis das helikale Äquivalent eines regulären Polygons. Dieser Fall wird als n-fache Helixsymmetrie bezeichnet , wobei n = 360 ° ist (wie im Fall einer Doppelhelix ). Dieses Konzept kann weiter verallgemeinert werden, um Fälle einzuschließen, in denen ein Vielfaches von 360 ° vorliegt - das heißt, der Zyklus wiederholt sich schließlich, jedoch erst nach mehr als einer vollständigen Umdrehung des helikalen Objekts.
- Nicht wiederholte helikale Symmetrie : Dies ist der Fall, in dem der zur Beobachtung der Symmetrie erforderliche Drehwinkel θ irrational ist . Der Drehwinkel wiederholt sich nie genau, egal wie oft die Helix gedreht wird. Solche Symmetrien werden unter Verwendung einer sich nicht wiederholenden Punktgruppe in zwei Dimensionen erzeugt . DNA mit ungefähr 10,5 Basenpaaren pro Umdrehung ist ein Beispiel für diese Art von sich nicht wiederholender helikaler Symmetrie.
Doppelte Rotationssymmetrie

In 4D kann eine Doppelrotationssymmetrie als Verbund zweier orthogonaler Rotationen erzeugt werden. Es ähnelt der 3D-Schraubenachse, die sich aus einer Rotation und einer orthogonalen Translation zusammensetzt.
Nichtisometrische Symmetrien
Eine breitere Definition der geometrischen Symmetrie ermöglicht Operationen aus einer größeren Gruppe als der euklidischen Gruppe von Isometrien. Beispiele für größere geometrische Symmetriegruppen sind:
- Die Gruppe der Ähnlichkeitstransformationen ; dh affine Transformationen, dargestellt durch eine Matrix A , die skalar mal eine orthogonale Matrix ist . Somit wird Homothetik hinzugefügt, Selbstähnlichkeit wird als Symmetrie betrachtet.
- Die Gruppe affiner Transformationen, dargestellt durch eine Matrix A mit Determinante 1 oder -1; dh die Transformationen, die Fläche erhalten.
- Dies fügt beispielsweise eine schräge Reflexionssymmetrie hinzu .
- Die Gruppe aller bijektiven affinen Transformationen .
- Die Gruppe der Möbius-Transformationen, die Kreuzverhältnisse bewahren .
- Dies fügt beispielsweise inversive Reflexionen wie Kreisreflexionen in der Ebene hinzu.
In Felix Klein ‚s Erlangen Programm jede mögliche Gruppe von Symmetrien definiert eine Geometrie , in der Objekte , die von einem Mitglied der Symmetriegruppe äquivalent betrachtet werden verwandt sind. Beispielsweise definiert die euklidische Gruppe die euklidische Geometrie , während die Gruppe der Möbius-Transformationen die projektive Geometrie definiert .
Skalensymmetrie und Fraktale

Skalensymmetrie bedeutet, dass das neue Objekt beim Erweitern oder Verkleinern eines Objekts dieselben Eigenschaften wie das Original hat. Dies gilt nicht für die meisten physikalischen Systeme, wie der Unterschied in der Form der Beine eines Elefanten und einer Maus zeigt (sogenannte allometrische Skalierung ). In ähnlicher Weise würde eine weiche Wachskerze, wenn sie auf die Größe eines hohen Baumes vergrößert würde, sofort unter ihrem eigenen Gewicht zusammenbrechen.
Eine subtilere Form der Skalensymmetrie wird durch Fraktale demonstriert . Nach der Vorstellung von Benoît Mandelbrot sind Fraktale ein mathematisches Konzept, bei dem die Struktur einer komplexen Form bei jedem Vergrößerungsgrad ähnlich aussieht , was in der Mandelbrot-Menge gut zu sehen ist . Eine Küste ist ein Beispiel für ein natürlich vorkommendes Fraktal, da sie auf jeder Ebene von der Ansicht eines Satelliten bis zu einer mikroskopischen Untersuchung, wie das Wasser gegen einzelne Sandkörner aufschlägt, eine ähnlich aussehende Komplexität beibehält. Ein weiteres Beispiel ist die Verzweigung von Bäumen, die es kleinen Zweigen ermöglicht, in Dioramen für volle Bäume zu stehen .
Da Fraktale das Auftreten von Mustern in der Natur erzeugen können , haben sie eine Schönheit und Vertrautheit, die bei mathematisch erzeugten Funktionen normalerweise nicht zu sehen ist. Fraktale haben auch einen Platz in computergenerierten Filmeffekten gefunden , wo ihre Fähigkeit, komplexe Kurven mit fraktalen Symmetrien zu erstellen, zu realistischeren virtuellen Welten führt .
Abstrakte Symmetrie
Kleins Ansicht
Felix Klein hat mit jeder Geometrie eine zugrunde liegende Gruppe von Symmetrien verknüpft . Die Hierarchie der Geometrien wird somit mathematisch als Hierarchie dieser Gruppen und Hierarchie ihrer Invarianten dargestellt . Beispielsweise bleiben Längen, Winkel und Flächen in Bezug auf die euklidische Symmetriegruppe erhalten, während bei den allgemeinsten projektiven Transformationen nur die Inzidenzstruktur und das Kreuzverhältnis erhalten bleiben . Ein Konzept der Parallelität , das in der affinen Geometrie erhalten bleibt , ist in der projektiven Geometrie nicht sinnvoll . Dann wird durch die zugrunde liegenden abstrahiert Gruppen von Symmetrien von den Geometrien können die Beziehungen zwischen ihnen auf Konzernebene wieder hergestellt. Da die Gruppe der affinen Geometrie ist eine Untergruppe der Gruppe der projektiven Geometrie ist jeder Begriff invariant in projektiven Geometrie a priori aussagekräftig in affiner Geometrie; aber nicht umgekehrt. Wenn Sie die erforderlichen Symmetrien hinzufügen, haben Sie eine leistungsfähigere Theorie, aber weniger Konzepte und Theoreme (die tiefer und allgemeiner sind).
Thurstons Ansicht
William Thurston führte eine ähnliche Version von Symmetrien in der Geometrie ein. Eine Modellgeometrie ist ein einfach verbundener glatter Verteiler X zusammen mit einer transitiven Wirkung einer Lie-Gruppe G auf X mit kompakten Stabilisatoren. Die Lie-Gruppe kann als die Gruppe von Symmetrien der Geometrie betrachtet werden.
Eine Modellgeometrie wird als maximal bezeichnet, wenn G unter Gruppen, die mit kompakten Stabilisatoren reibungslos und transitiv auf X wirken , maximal ist, dh wenn es sich um die maximale Gruppe von Symmetrien handelt. Manchmal ist diese Bedingung in der Definition einer Modellgeometrie enthalten.
Eine geometrische Struktur auf einer Mannigfaltigkeit M ist ein Diffeomorphismus von M nach X / Γ für einige Modellgeometrien X , wobei Γ eine diskrete Untergruppe von G ist, die frei auf X wirkt . Wenn eine gegebene Mannigfaltigkeit eine geometrische Struktur zulässt, dann lässt sie eine zu, deren Modell maximal ist.
Eine dreidimensionale Modellgeometrie X ist für die Geometrisierungsvermutung relevant, wenn sie maximal ist und wenn mindestens ein kompakter Verteiler mit einer nach X modellierten geometrischen Struktur vorhanden ist . Thurston klassifizierte die 8 Modellgeometrien, die diese Bedingungen erfüllen. Sie sind unten aufgeführt und werden manchmal als Thurston-Geometrien bezeichnet . (Es gibt auch unzählige Modellgeometrien ohne kompakte Quotienten.)




