Fleißiger Biber - Busy beaver
In der theoretischen Informatik , die damit beschäftigt Biber Spiel zielt auf eine Beendigung der Suche nach Programm einer bestimmten Größe, die die meisten Ausgabe möglich erzeugt. Da ein endlos Looping Programm unendlich Ausgang erzeugt leicht konzipiert ist, werden solche Programme aus dem Spiel ausgeschlossen.
Genauer gesagt besteht das geschäftige Biberspiel darin, eine anhaltende Turing-Maschine mit binärem Alphabet zu entwerfen, die die meisten Einsen auf das Band schreibt, wobei nur eine bestimmte Menge von Zuständen verwendet wird. Die Regeln für das 2-State-Spiel sind wie folgt:
- die Maschine muss zusätzlich zum anhaltenden Zustand zwei Zustände haben, und
- das Band enthält zunächst nur 0s.
Ein Spieler sollte eine Übergangstabelle konzipieren, die auf die längste Ausgabe von 1s auf dem Band abzielt, während er sicherstellt, dass die Maschine irgendwann anhält.
Ein n- ter beschäftigter Biber , BB- n oder einfach "beschäftigter Biber" ist eine Turing-Maschine, die das n- State Busy Beaver Game gewinnt . Das heißt, sie erreicht die größte Zahl von Einsen unter allen anderen möglichen konkurrierenden n- Zustands-Turingmaschinen. Die BB-2 Turing-Maschine zum Beispiel erreicht vier Einsen in sechs Schritten.
Ob eine beliebige Turingmaschine ein fleißiger Biber ist, ist unentscheidbar . Dies hat Auswirkungen auf die Berechenbarkeitstheorie , das Halteproblem und die Komplexitätstheorie . Das Konzept wurde erstmals von Tibor Radó in seinem 1962 erschienenen Aufsatz "Über nicht berechenbare Funktionen" eingeführt.
Das Spiel
Das n- State Busy Beaver Game (oder BB- n Game ), das in Tibor Radós Papier von 1962 eingeführt wurde, umfasst eine Klasse von Turing-Maschinen , von denen jedes Mitglied die folgenden Designspezifikationen erfüllen muss:
- Die Maschine hat n "operative" Zustände plus einen Halt-Zustand, wobei n eine positive ganze Zahl ist und einer der n Zustände als Startzustand unterschieden wird. (Normalerweise werden die Zustände mit 1, 2, ..., n , mit Zustand 1 als Startzustand, oder mit A , B , C , ..., mit Zustand A als Startzustand bezeichnet.)
- Die Maschine verwendet ein einzelnes, unendliches (oder unbegrenztes) Zweiwege-Band.
- Das Bandalphabet ist {0, 1}, wobei 0 als Leerzeichen dient.
- Die Übergangsfunktion der Maschine benötigt zwei Eingaben:
- der aktuelle Nicht-Halt-Zustand,
- das Symbol in der aktuellen Bandzelle,
- und erzeugt drei Ausgaben:
- ein Symbol zum Überschreiben des Symbols in der aktuellen Bandzelle (es kann dasselbe Symbol sein wie das überschriebene Symbol),
- eine Bewegungsrichtung (nach links oder rechts; d. h. eine Stelle links oder rechts von der aktuellen Zelle zur Bandzelle verschieben) und
- ein Zustand, in den übergegangen werden soll (der der Halt-Zustand sein kann).
- Es gibt also (4 n + 4) 2 n n -Zustands-Turingmaschinen, die diese Definition erfüllen, weil die allgemeine Form der Formel ( Symbole × Richtungen × ( Zustände + 1)) ( Symbole × Zustände ) ist .
- Die Übergangsfunktion kann als endliche Tabelle von 5-Tupeln betrachtet werden, jedes der Form
- (aktueller Zustand, aktuelles Symbol, zu schreibendes Symbol, Verschiebungsrichtung, nächster Zustand).
Das "Laufen" der Maschine besteht darin, im Startzustand zu starten, wobei die aktuelle Bandzelle eine beliebige Zelle eines leeren (alles-0)-Bandes ist, und dann die Übergangsfunktion zu wiederholen, bis in den Halt-Zustand eingetreten wird (wenn überhaupt). Wenn die Maschine schließlich anhält, und nur wenn, dann wird die Anzahl der Einsen, die schließlich auf dem Band verbleiben, als Score der Maschine bezeichnet .
Das n- State Busy Beaver (BB- n )-Spiel ist ein Wettbewerb, um eine solche n- State Turing-Maschine mit der größtmöglichen Punktzahl zu finden – die größte Anzahl von Einsen auf ihrem Band nach dem Anhalten. Eine Maschine , die erreicht die größtmögliche Punktzahl unter allen n -state Turingmaschinen ist ein genannt n -state beschäftigt Biber, und eine Maschine , deren Partitur ist nur die höchste bisher erreichte (vielleicht nicht die größte möglich) ist ein sogenannter Champion n -state Maschine.
Radó verlangte, dass jede am Wettbewerb teilnehmende Maschine von einer genauen Anzahl von Schritten begleitet wird, die erforderlich sind, um den Halt-Zustand zu erreichen, sodass die Punktzahl jeder Teilnahme (im Prinzip) überprüft werden kann, indem die Maschine für die angegebene Anzahl betrieben wird von Schritten. (Wenn Einträge nur aus Maschinenbeschreibungen bestehen würden, dann ist das Problem, jeden potentiellen Eintrag zu verifizieren, unentscheidbar, weil es dem wohlbekannten Anhalteproblem entspricht — es gäbe keinen effektiven Weg zu entscheiden, ob eine beliebige Maschine schließlich anhält.)
Verwandte Funktionen
Die fleißige Biber-Funktion Σ
Die Busy Beaver-Funktion quantifiziert die maximale Punktzahl, die von einem Busy Beaver bei einem gegebenen Takt erreicht werden kann. Dies ist eine nicht berechenbare Funktion . Außerdem kann gezeigt werden, dass eine Busy-Beaver-Funktion asymptotisch schneller wächst als jede berechenbare Funktion.
Die Busy-Beaver-Funktion Σ: ℕ → ℕ ist so definiert, dass Σ( n ) die maximal erreichbare Punktzahl (die maximale Anzahl von Einsen schließlich auf dem Band) unter allen anhaltenden 2-Symbol- n- Zustands-Turingmaschinen der oben genannten beschriebenen Art, wenn auf einem leeren Band gestartet.
Es ist klar, dass Σ eine wohldefinierte Funktion ist: Für jedes n gibt es höchstens endlich viele n- Zustands-Turingmaschinen wie oben, bis auf Isomorphie, also höchstens endlich viele mögliche Laufzeiten.
Diese unendliche Folge Σ ist die damit beschäftigt Biberfunktion , und jedes n -state 2-Symbol - Turingmaschine M , für die σ ( M ) = Σ ( n ) (dh, die die maximale Punktzahl erreicht) ist ein sogenannter beschäftigt Beaver . Beachten Sie, dass es für jedes n mindestens vier beschäftigte Biber mit n Zuständen gibt (weil bei jedem beschäftigten Biber mit n Zuständen ein anderer durch bloßes Ändern der Verschiebungsrichtung in einem anhaltenden Übergang erhalten wird, ein anderer durch Verschieben aller Richtungsänderungen in ihre entgegengesetzte Richtung , und das letzte durch Verschieben der Halt-Richtung des all-Swapped Busy Bibers).
Nicht-Berechenbarkeit
Radós Arbeit von 1962 bewies, dass wenn f : ℕ → ℕ irgendeine berechenbare Funktion ist , dann Σ( n ) > f(n) für alle hinreichend großen n , und daher ist Σ keine berechenbare Funktion.
Darüber hinaus bedeutet dies , dass es unentscheidbar durch einen allgemeinen Algorithmus , ob eine beliebige Turingmaschine ein arbeitsreiches Biber ist. (Ein solcher Algorithmus kann nicht existieren, weil seine Existenz die Berechnung von Σ erlauben würde, was eine erwiesene Unmöglichkeit ist. Insbesondere könnte ein solcher Algorithmus verwendet werden, um einen anderen Algorithmus zu konstruieren, der Σ wie folgt berechnet: für jedes gegebene n ist jedes von die endlich viele n -state 2-Symbol - Turing Maschinen getestet werden würden , bis ein n -state beschäftigt Biber gefunden wird, das damit beschäftigt Biber Maschine dann seine Kerbe würde simuliert , um zu bestimmen, die per Definition ist Σ ( n )).
Obwohl Σ( n ) eine unberechenbare Funktion ist, gibt es einige kleine n, für die es möglich ist, ihre Werte zu erhalten und ihre Richtigkeit zu beweisen. Es ist nicht schwer zu zeigen, dass Σ(0) = 0, Σ(1) = 1, Σ(2) = 4, und mit zunehmender Schwierigkeit kann gezeigt werden, dass Σ(3) = 6 und Σ(4) = 13 (Sequenz A028444 im OEIS ). Σ( n ) wurde noch für keinen Fall von n > 4 bestimmt, obwohl untere Schranken festgelegt wurden (siehe Abschnitt Bekannte Werte weiter unten).
Im Jahr 2016 erhielten Adam Yedidia und Scott Aaronson die erste (explizite) obere Schranke für das Minimum n, für das Σ( n ) in ZFC nicht beweisbar ist . Dazu konstruierten sie eine 7910-Zustands-Turingmaschine, deren Verhalten nicht mit den üblichen Axiomen der Mengenlehre ( Zermelo-Fraenkel-Mengentheorie mit dem Wahlaxiom ) unter vernünftigen Konsistenzhypothesen ( stationäre Ramsey-Eigenschaft ) bewiesen werden kann . Dies wurde später auf 1919 Staaten reduziert, wobei die Abhängigkeit vom stationären Ramsey-Grundstück beseitigt wurde, und später auf 748 Staaten.
Komplexität und Unbeweisbarkeit von Σ
Eine Variante der Kolmogorov-Komplexität wird wie folgt definiert [vgl. Boolos, Burgess & Jeffrey, 2007]: Die Komplexität einer Zahl n ist die kleinste Anzahl von Zuständen, die für eine Turing-Maschine der BB-Klasse benötigt wird, die mit einem einzelnen Block von n aufeinanderfolgenden Einsen auf einem anfänglich leeren Band anhält . Die entsprechende Variante des Unvollständigkeitssatzes von Chaitin besagt, dass es im Kontext eines gegebenen axiomatischen Systems für die natürlichen Zahlen eine Zahl k gibt, so dass keine spezifische Zahl mit größerer Komplexität als k nachgewiesen werden kann , und somit keine spezifische obere Schranke kann für Σ( k ) bewiesen werden (letzteres liegt daran, dass "die Komplexität von n größer als k " wäre, wenn " n > Σ( k )" bewiesen wäre). Wie in der zitierten Referenz erwähnt, ist für jedes axiomatische System der "gewöhnlichen Mathematik" der kleinste Wert k, für den dies zutrifft, weit kleiner als 10↑↑10 ; folglich kann im Kontext der gewöhnlichen Mathematik weder der Wert noch eine obere Schranke von Σ(10 ↑↑ 10) bewiesen werden. ( Gödels erster Unvollständigkeitssatz wird durch dieses Ergebnis illustriert: In einem axiomatischen System der gewöhnlichen Mathematik gibt es einen wahr-aber-unbeweisbaren Satz der Form "Σ(10 ↑↑ 10) = n ", und es gibt unendlich viele wahr- aber nicht beweisbare Sätze der Form "Σ(10 ↑↑ 10) < n ".)
Maximale Verschiebungen Funktion S
Neben der Funktion Σ führte Radó [1962] eine weitere Extremfunktion für die BB-Klasse von Turingmaschinen ein, die Maximum-Shifts-Funktion , S , definiert wie folgt:
- s ( M ) = die Anzahl der Verschiebungen, die M vor dem Anhalten macht, für jedes M in E n ,
- S ( n ) = max{ s ( M ) | M ∈ E n } = die größte Anzahl von Verschiebungen, die von einer anhaltenden n- Zustands-2-Symbol-Turingmaschine ausgeführt werden.
Da diese Turing-Maschinen bei jedem Übergang oder "Schritt" (einschließlich jedem Übergang in einen Halt-Zustand) eine Verschiebung haben müssen, ist die Max-Shifts-Funktion gleichzeitig eine Max-Steps-Funktion.
Radó zeigte, dass S aus dem gleichen Grund nicht berechenbar ist wie Σ – es wächst schneller als jede berechenbare Funktion. Er erwies sich diese einfach mit der Feststellung , dass für jedes n , S ( n ) ≥ Σ ( n ). Jede Verschiebung kann eine 0 oder eine 1 auf das Band schreiben, während Σ eine Teilmenge der Verschiebungen zählt, die eine 1 geschrieben haben, nämlich diejenigen, die zum Zeitpunkt des Anhaltens der Turing-Maschine noch nicht überschrieben waren; folglich wächst S mindestens so schnell wie Σ, von dem bereits nachgewiesen wurde, dass es schneller wächst als jede berechenbare Funktion.
Die folgende Verbindung zwischen Σ und S wurde von Lin & Radó [ Computer Studies of Turing Machine Problems , 1965] verwendet, um zu beweisen, dass Σ(3) = 6: Für ein gegebenes n , wenn S ( n ) bekannt ist, dann sind alle n- Zustände Turing-Maschinen können (im Prinzip) bis zu S ( n ) Schritte laufen , wobei jede Maschine, die noch nicht angehalten hat, nie mehr anhält. An diesem Punkt erhält man aus ihren Bändern den Wert von Σ( n ). Der von Lin & Radó verwendete Ansatz für den Fall von n = 3 bestand darin, S (3) = 21 zu vermuten und dann alle im Wesentlichen unterschiedlichen 3-Zustandsautomaten für bis zu 21 Schritte zu simulieren. Durch das Verhalten der Maschinen zu analysieren , die innerhalb von 21 Schritten nicht angehalten hatte, gelang es ihnen , dass keine dieser Maschinen zeigt jemals halt, so dass die Vermutung , was beweist , dass S (3) 21 =, und Bestimmen , dass Σ (3) = 6 durch das eben beschriebene Verfahren.
Ungleichungen bezüglich Σ und S beinhalten die folgenden (aus [Ben-Amram, et al., 1996]), die für alle n ≥ 1 gelten :
und ein asymptotisch verbesserte gebunden (aus [Ben-Amram, Petersen, 2002]): Es existiert eine Konstante C , so daß für alle n ≥ 2 ,
neigt dazu, in der Nähe des Quadrats von zu liegen , und tatsächlich geben viele Maschinen weniger als aus .
Bekannte Werte für Σ und S
Ab 2016 sind die Funktionswerte für Σ( n ) und S ( n ) nur noch für n < 5 exakt bekannt .
Der aktuelle (Stand 2018) 5-Staaten-Meister der fleißigen Biber produziert 4098 1s, mit47 176 870 Schritte (entdeckt von Heiner Marxen und Jürgen Buntrock 1989), aber es bleiben 18 oder 19 (möglicherweise unter 10, siehe unten) Maschinen mit unregelmäßigem Verhalten, von denen angenommen wird, dass sie niemals anhalten, die jedoch nicht nachgewiesen wurden unendlich laufen. Skelett listet 42 oder 43 unbewiesene Maschinen auf, aber 24 sind bereits bewiesen. Die verbleibenden Maschinen wurden auf 81,8 Milliarden Schritte simuliert, aber keiner wurde angehalten. Daniel Briggs hat auch einige Maschinen bewiesen. Eine andere Quelle sagt, dass 98 Maschinen unbewiesen bleiben. Es gibt eine Analyse der Holdouts. Es ist also wahrscheinlich, dass Σ(5) = 4098 und S(5) = 47176870, aber dies bleibt unbewiesen, und es ist unbekannt, ob es noch Reste gibt (Stand 2018). Im Moment produziert der Rekordmeister mit 6 Staaten über3.515 × 10 18 267 1s (genau (25×4 30341 +23)/9), mit Über7,412 × 10 36 534 Schritte (von Pavel Kropitz im Jahr 2010 gefunden). Wie oben erwähnt, handelt es sich um 2-Symbol-Turing-Maschinen.
Eine einfache Erweiterung der 6-Zustandsmaschine führt zu einer 7-Zustandsmaschine, die mehr als 10 10 10 10 . schreibt18 705 353 1s auf dem Band, aber es gibt zweifellos viel beschäftigtere 7-State-Maschinen. Andere vielbeschäftigte Biberjäger haben jedoch andere Maschinensätze.
Milton Green konstruierte in seinem 1964 erschienenen Artikel "A Lower Bound on Rado's Sigma Function for Binary Turing Machines" eine Reihe von Turing-Maschinen, die dies demonstrieren
wobei ↑ die Knuth-Aufwärtspfeil-Notation ist und A die Ackermann-Funktion ist .
Daher
(mit 3 3 3 = 7 625 597 484 987 Terme im Exponentialturm) und
wobei die Zahl g 1 der enorme Startwert in der Folge ist, die Grahams Zahl definiert .
1964 entwickelte Milton Green eine untere Schranke für die Busy Beaver-Funktion, die im Tagungsband des IEEE-Symposiums 1964 über Schaltkreistheorie und logisches Design veröffentlicht wurde. Heiner Marxen und Jürgen Buntrock beschrieben es als "eine nicht triviale (nicht primitiv rekursive) untere Grenze". Diese untere Grenze kann berechnet werden, ist jedoch zu komplex, um sie als einzelnen Ausdruck in Bezug auf n anzugeben. Bei n=8 ergibt das Verfahren Σ(8) ≥ 3 × (7 × 3 92 - 1) / 2 ≈ 8,248×10 44 .
Aus den aktuellen unteren Schranken kann abgeleitet werden, dass:
Im Gegensatz dazu ist die beste aktuelle (Stand 2018) untere Schranke für Σ(6) 10 18 267 , was größer ist als die untere Grenze der Greenschen Formel, 3 3 = 27 (was im Vergleich winzig ist). Tatsächlich ist es viel größer als die untere Grenze: 3 ↑↑ 3 = 3 3 3 =7 625 597 484 987 , was Greens erste untere Schranke für Σ(8) ist, und auch viel größer als die zweite untere Schranke: 3×(7×3 92 −1)/2.
Σ(7) ist auf die gleiche Weise viel, viel größer als die derzeitige gemeinsame untere Schranke 3 31 (fast 618 Billionen), also ist auch die zweite untere Schranke sehr, sehr schwach.
Beweis für Unberechenbarkeit von S ( n ) und Σ( n )
Angenommen, S ( n ) sei eine berechenbare Funktion, und EvalS bezeichne eine TM, die S ( n ) auswertet . Bei einem Band mit n 1s erzeugt es S ( n ) 1s auf dem Band und hält dann an. Lassen Sie Clean eine Turing-Maschine bezeichnen, die die Sequenz von 1s reinigt, die ursprünglich auf das Band geschrieben wurde. Lassen Doppel bezeichnen eine Turing - Maschine - Funktion Auswertung n + n . Bei einem Band mit n 1s werden 2 n 1s auf dem Band produziert und dann angehalten. Erstellen wir die Komposition Double | Auswertungen | Bereinigen und sei n 0 die Anzahl der Zustände dieser Maschine. Lassen Sie Create_n 0 eine Turing-Maschine bezeichnen, die n 0 1s auf einem anfänglich leeren Band erzeugt. Diese Maschine kann auf triviale Weise so konstruiert sein, dass sie n 0 Zustände hat (der Zustand i schreibt 1, bewegt den Kopf nach rechts und schaltet in den Zustand i + 1 um, mit Ausnahme des Zustands n 0 , der anhält). Sei N die Summe n 0 + n 0 .
Sei BadS die Zusammensetzung Create_n 0 | Doppel | Auswertungen | Sauber . Beachten Sie, dass diese Maschine N Zustände hat. Ausgehend von einem zunächst leeren Band erstellt es zunächst eine Sequenz von n 0 1s und verdoppelt diese dann zu einer Sequenz von N 1s. Dann SchlechtS produzieren S ( N ) 1 s auf Band, und schließlich wird es alle 1s löschen und dann stoppen. Aber die Reinigungsphase wird mindestens S ( N ) Schritte dauern , so dass die Arbeitszeit von BadS strikt länger als S ( N ) ist, was der Definition der Funktion S ( n ) widerspricht .
Die Unberechenbarkeit von Σ( n ) lässt sich auf ähnliche Weise beweisen. Im obigen Beweis muss man die Maschine EvalS mit EvalΣ und Clean mit Increment austauschen – ein einfaches TM, das nach einer ersten 0 auf dem Band sucht und diese durch 1 ersetzt.
Die Unberechenbarkeit von S ( n ) kann auch unter Bezugnahme auf das Problem des Anhaltens des leeren Bandes festgestellt werden. Das Problem des Anhaltens eines leeren Bandes ist das Problem der Entscheidung für jede Turing-Maschine, ob sie anhält oder nicht, wenn sie mit einem leeren Band gestartet wird. Das Halteproblem für leere Bänder entspricht dem standardmäßigen Halteproblem und ist daher ebenfalls nicht berechenbar. Wenn S ( n ) berechenbar wäre, dann könnten wir das Problem des Anhaltens des leeren Bandes einfach lösen, indem wir eine beliebige Turingmaschine mit n Zuständen für S ( n ) Schritte laufen lassen ; wenn es immer noch nicht aufgehört hat, wird es es nie tun. Da das Problem des Anhaltens des leeren Bandes nicht berechenbar ist, folgt daraus, dass S ( n ) ebenfalls nicht berechenbar sein muss.
Verallgemeinerungen
Für jedes Berechnungsmodell gibt es einfache Analoga des beschäftigten Bibers. Zum Beispiel definiert die Verallgemeinerung auf Turing-Maschinen mit n Zuständen und m Symbolen die folgenden verallgemeinerten Busy-Beaver-Funktionen :
- Σ( n , m ): die größte Anzahl von Nicht-Nullen, die von einer n- Zustands- m- Symbol-Maschine gedruckt werden kann, die auf einem anfänglich leeren Band gestartet wurde, bevor sie angehalten wurde , und
- S ( n , m ): die größte Anzahl von Schritten, die von einer n- Zustands- m- Symbol-Maschine ausgeführt werden, die auf einem anfänglich leeren Band gestartet wurde, bevor sie angehalten wurde .
Zum Beispiel läuft die am längsten laufende 3-Zustands-3-Symbol-Maschine, die bisher gefunden wurde 119 112 334 170 342 540 Schritte vor dem Anhalten. Die am längsten laufende Maschine mit 6 Zuständen und 2 Symbolen, die die zusätzliche Eigenschaft hat, den Bandwert bei jedem Schritt umzukehren, produziert6147 1s nach47 339 970 Schritte. Also S RTM (6)47 339 970 und RTM (6) ≥6147 .
Es ist möglich, die Busy-Beaver-Funktion weiter zu verallgemeinern, indem man sie auf mehr als eine Dimension ausdehnt.
Ebenso könnten wir eine Analogie zur Σ-Funktion für Registermaschinen als die größte Zahl definieren, die beim Anhalten in einem beliebigen Register für eine gegebene Anzahl von Befehlen vorhanden sein kann.
Genaue Werte und Untergrenzen
Die folgende Tabelle listet die genauen Werte und einige bekannte untere Grenzen für S ( n , m ) und ( n , m ) für die verallgemeinerten Beschäftigt-Biber-Probleme auf. Hinweis: Einträge, die als "?" werden von unten durch das Maximum aller Einträge nach links und oben begrenzt. Diese Maschinen wurden entweder nicht untersucht oder wurden nachträglich von einer kleineren Maschine übertroffen.
Die Turing-Maschinen, die diese Werte erreichen, sind auf der Webseite von Pascal Michel verfügbar . Jede dieser Websites enthält auch einige Analysen der Turing-Maschinen und Verweise auf die Beweise für die genauen Werte.
Werte von S( n , m ) nm2-Zustand 3-Zustand 4-Zustand 5-Staaten 6-Zustand 7-Staaten 2-Symbol 6 21 107 47 176 870 ? > 7,4 × 10 36 534 > 10 10 10 1018 705 353 3-Symbol 38 ≥ 119 112 334 170 342 540 > 1,0 × 10 14 072 ? ? ? 4-Symbol ≥ 3 932 964 > 5,2 × 10 13 036 ? ? ? ? 5-Symbol > 1,9 × 10 704 ? ? ? ? ? 6-Symbol > 2,4 × 10 9866 ? ? ? ? ? Werte von Σ( n , m ) nm2-Zustand 3-Zustand 4-Zustand 5-Staaten 6-Zustand 7-Staaten 2-Symbol 4 6 13 4098 ? > 3,5 × 10 18 267 > 10 10 10 1018 705 353 3-Symbol 9 ≥ 374 676 383 > 1,3 × 10 7036 ? ? ? 4-Symbol ≥ 2050 > 3,7 × 10 6518 ? ? ? ? 5-Symbol > 1,7 × 10 352 ? ? ? ? ? 6-Symbol > 1,9 × 10 4933 ? ? ? ? ?
Nichtdeterministische Turingmaschinen
| P | Schritte | Zustände |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | fünfzehn |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
Das Problem kann auf nichtdeterministische Turingmaschinen erweitert werden, indem nach dem System mit den meisten Zuständen über alle Zweige oder dem Zweig mit der längsten Anzahl von Schritten gesucht wird. Die Frage, ob ein gegebener NDTM anhält, ist immer noch rechnerisch irreduzibel, und die Berechnung, die erforderlich ist, um einen NDTM-beschäftigten Biber zu finden, ist erheblich größer als im deterministischen Fall, da mehrere Verzweigungen berücksichtigt werden müssen. Für ein 2-Zustands-, 2-Farben-System mit p Fällen oder Regeln gibt die Tabelle rechts die maximale Anzahl von Schritten vor dem Anhalten und die maximale Anzahl von eindeutigen Zuständen an, die von der NDTM erzeugt werden.
Anwendungen
Abgesehen davon, dass sie ein ziemlich anspruchsvolles mathematisches Spiel darstellen , bieten die beschäftigten Biber-Funktionen einen völlig neuen Ansatz zur Lösung rein mathematischer Probleme. Viele offene Probleme in der Mathematik könnten theoretisch, aber nicht praktisch, systematisch gelöst werden, wenn der Wert von S ( n ) für ein ausreichend großes n gegeben ist .
Betrachten Sie jede Vermutung , die durch ein Gegenbeispiel aus einer abzählbaren Anzahl von Fällen widerlegt werden könnte (z. B. die Vermutung von Goldbach ). Schreiben Sie ein Computerprogramm, das diese Vermutung nacheinander auf steigende Werte prüft. Im Fall der Goldbachschen Vermutung würden wir jede gerade Zahl 4 sequentiell betrachten und prüfen, ob sie die Summe zweier Primzahlen ist oder nicht. Angenommen, dieses Programm wird auf einer n- Zustands-Turingmaschine simuliert . Wenn es ein Gegenbeispiel findet (eine gerade Zahl 4, die in unserem Beispiel nicht die Summe zweier Primzahlen ist), hält es an und zeigt dies an. Wenn die Vermutung jedoch zutrifft, wird unser Programm niemals anhalten. (Dieses Programm hält nur an, wenn es ein Gegenbeispiel findet.)
Nun, dieses Programm wird durch eine Turingmaschine mit n Zuständen simuliert. Wenn wir also S ( n ) kennen, können wir (in endlicher Zeit) entscheiden, ob es jemals anhalten wird oder nicht, indem wir die Maschine einfach so viele Schritte ausführen. Und wenn die Maschine nach S ( n ) Schritten nicht anhält, wissen wir, dass sie dies niemals tun wird und somit keine Gegenbeispiele zu der gegebenen Vermutung existieren (dh keine geraden Zahlen, die nicht die Summe zweier Primzahlen sind). Damit würde sich die Vermutung bewahrheiten.
Somit könnten spezifische Werte (oder obere Schranken) für S ( n ) verwendet werden, um viele offene Probleme in der Mathematik (theoretisch) systematisch zu lösen. Aktuelle Ergebnisse zum Beschäftigt-Biber-Problem deuten jedoch darauf hin, dass dies aus zwei Gründen nicht praktikabel sein wird:
- Es ist extrem schwierig, Werte für die Busy-Beaver-Funktion (und die Max-Shift-Funktion) zu beweisen. Es hat sich nur für extrem kleine Maschinen mit weniger als fünf Zuständen bewährt, während man vermutlich mindestens 20-50 Zustände braucht, um eine brauchbare Maschine zu bauen. Darüber hinaus wurde jeder bekannte exakte Wert von S ( n ) bewiesen, indem jede Turingmaschine mit n Zuständen aufgezählt und bewiesen wurde, ob jede anhält oder nicht. Man müsste S ( n ) mit einer weniger direkten Methode berechnen, damit es tatsächlich nützlich ist.
- Aber selbst wenn man einen besseren Weg zur Berechnung von S ( n ) gefunden hätte, werden die Werte der Busy Beaver-Funktion (und der Max-Shift-Funktion) sehr schnell sehr groß. S (6) > 1036 534 erfordert bereits eine spezielle musterbasierte Beschleunigung, um vollständig simulieren zu können. Ebenso wissen wir, dass S (10) > Σ(10) > 3 ↑↑↑ 3 eine riesige Zahl ist und S (17) > Σ(17) > G, wobei G die Grahamsche Zahl ist – eine enorme Zahl. Selbst wenn wir, sagen wir, S (30)wüssten,ist es daher völlig unvernünftig, eine Maschine mit dieser Anzahl von Schritten laufen zu lassen. Es gibt nicht genug Rechenkapazität im bekannten Teil des Universums, um auch nur S (6) Operationen direkt ausführen zu können.
Bemerkenswerte Fälle
Eine binäre Turing-Maschine mit 748 Zuständen wurde konstruiert, die anhält, wenn ZFC inkonsistent ist. Eine Turingmaschine mit 744 Zuständen wurde konstruiert, die anhält, wenn die Riemannsche Hypothese falsch ist. Eine Turingmaschine mit 43 Zuständen wurde konstruiert, die anhält, falls die Goldbachsche Vermutung falsch ist, und eine 27-Zustandsmaschine für diese Vermutung wurde vorgeschlagen, aber noch nicht verifiziert.
Eine Turingmaschine mit 15 Zuständen wurde konstruiert, die anhält, wenn die folgende Vermutung von Paul Erdős aus dem Jahr 1979 falsch ist: Für alle n > 8 gibt es mindestens eine Ziffer 2 in der Basis-3-Darstellung von 2 n .
Beispiele
Dies sind Regeltabellen für die Turingmaschinen, die (1) und S (1), Σ(2) und S (2), Σ(3) (aber nicht S (3)), Σ(4) und S . erzeugen (4) und die bekannteste untere Schranke für (5) und S (5) und Σ(6) und S (6). Für andere Visualisierungen,
In den Tabellen repräsentieren Spalten den aktuellen Status und Zeilen repräsentieren das aktuell vom Band gelesene Symbol. Jeder Tabelleneintrag ist eine Folge von drei Zeichen, die das auf das Band zu schreibende Symbol, die Bewegungsrichtung und den neuen Zustand (in dieser Reihenfolge) angibt. Der Halt-Zustand wird als H angezeigt .
Jede Maschine beginnt im Zustand A mit einem unendlichen Band, das alle Nullen enthält. Somit ist das vom Band gelesene Anfangssymbol eine 0.
Ergebnisschlüssel: (beginnt an der überstrichenen Position , endet an der unterstrichenen Position )
1-Zustand, 2-Symbol beschäftigt Biber EIN 0 1R H 1 (nicht benutzt)
Ergebnis: 0 0 1 0 0 (1 Schritt, insgesamt eine "1")
2-State, 2-Symbol beschäftigt Biber EIN B 0 1R B 1L A 1 1L B 1R H
Ergebnis: 0 0 1 1 1 1 0 0 (6 Schritte, insgesamt vier "1"en)
Beschäftigter Biber mit 3 Zuständen und 2 Symbolen EIN B C 0 1R B 0R C 1L C 1 1R H 1R B 1L A
Ergebnis: 0 0 1 1 1 1 1 1 0 0 (14 Schritte, insgesamt sechs "1"en).
Im Gegensatz zu den vorherigen Maschinen ist diese hier nur für Σ ein fleißiger Biber, aber nicht für S . ( S (3) = 21.)
Beschäftigter Biber mit 4 Zuständen und 2 Symbolen EIN B C D 0 1R B 1L A 1R H 1R D 1 1L B 0L C 1L D 0R A
Ergebnis: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 Schritte, insgesamt 13 "1"en)
aktueller 5-State, 2-Symbol bester Anwärter (möglicherweise beschäftigter Biber) EIN B C D E 0 1R B 1R C 1R D 1L A 1R H 1 1L C 1R B 0L E 1L D 0L A
Ergebnis: 4098 "1"en mit 8191 "0"en, eingestreut in 47.176.870 Schritten.
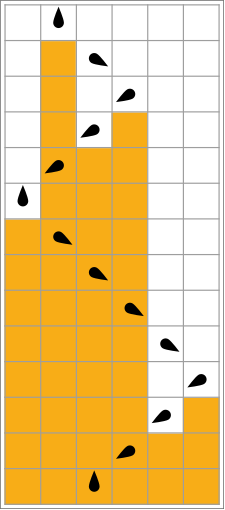
Beachten Sie in der Abbildung rechts, wie diese Lösung qualitativ der Evolution einiger zellularer Automaten ähnelt .
aktueller 6-State, 2-Symbol bester Anwärter EIN B C D E F 0 1R B 1R C 1L D 1R E 1L A 1L H 1 1L E 1R F 0R B 0L C 0R D 1R C
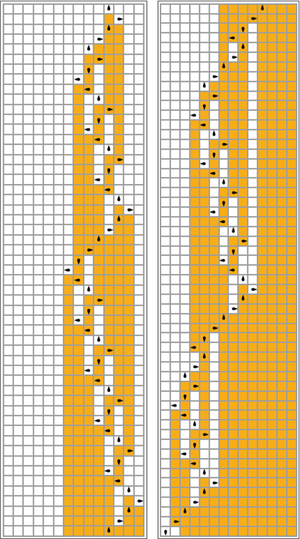
Ergebnis: ≈3,515 × 10 18267 "1"en in ≈7,412 × 10 36534 Schritten.
Visualisierungen
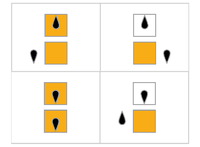
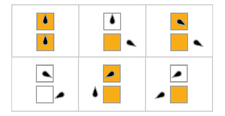
In der folgenden Tabelle sind die Regeln für jeden beschäftigten Biber (Maximierung von Σ) visuell dargestellt, wobei orange Quadrate einer "1" auf dem Band entsprechen und weiße Quadrate "0" entsprechen. Die Position des Kopfes wird durch das schwarze Oval angezeigt, wobei die Ausrichtung des Kopfes den Zustand repräsentiert. Einzelne Bänder werden horizontal ausgelegt, wobei die Zeit vertikal fortschreitet. Der Halt-Zustand wird durch eine Regel repräsentiert, die einen Zustand auf sich selbst abbildet (Kopf bewegt sich nicht).
Siehe auch
Anmerkungen
- ^ a b Radó, Tibor (Mai 1962). "Über nicht berechenbare Funktionen" (PDF) . Bell System Fachzeitschrift . 41 (3): 877–884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
- ^ Chaitin (1987)
- ^ Adam Yedidia und Scott Aaronson (Mai 2016). Eine relativ kleine Turingmaschine, deren Verhalten von der Mengenlehre unabhängig ist (Technischer Bericht). MIT. arXiv : 1605.04343 . Bibcode : 2016arXiv160504343Y .
- ^ Aron, Jakob. "Diese Turing-Maschine sollte ewig laufen, es sei denn, die Mathematik ist falsch" . Abgerufen 2016-09-25 .
- ^ a b Version vom 3. Mai enthielt 7918 Angaben: "Die 8000. Busy Beaver-Zahl entzieht sich der ZF-Mengentheorie" . Shtetl-optimierter Blog . 2016-05-03 . Abgerufen 2016-09-25 .
- ^ a b c "Drei Ansagen" . Shtetl-optimierter Blog . 2016-05-03 . Abgerufen am 27.04.2018 .
- ^ "GitHub - sorear/metamath-turing-machines: Metamath-Beweiszähler und andere Dinge" . 2019-02-13.
- ^ "Die geschäftige Bibergrenze" (PDF) .
- ^ "Skelet-Seite für Busy Beaver-Problem" . skelet.ludost.net .
- ^ Turing: Ein Projekt zur Fertigstellung von Busy Beaver von 5
- ^ „Das beschäftigte Biber-Problem: EIN NEUER MILLENNIUM-ANGRIFF“ .
- ^ a b Wolfram, Stephen (4. Februar 2021). "Mehrwege-Turing-Maschinen" . www.wolframphysik.org .
- ^ Chaitin 1987
- ^ Lloyd 2001. Rechenkapazität des Universums .
- ^ a b c Pavlus, Johannes (10. Dezember 2020). „Wie die langsamsten Computerprogramme die fundamentalen Grenzen der Mathematik beleuchten“ . Quanta-Magazin . Abgerufen 2020-12-11 .
- ^ Tristan Stérin und Damien Woods (Juli 2021). Zur Härte der Kenntnis der fleißigen Biberwerte BB(15) und BB(5,4) (Technischer Bericht). Maynooth-Universität. arXiv : 2107.12475 .
- ^ Erdõs, Paul (1979). "Einige unkonventionelle Probleme in der Zahlentheorie" . Mathematik. Mag. 52 (2): 67–70. doi : 10.1080/0025570X.1979.11976756 .
- ^ Lin, Shen; Rado, Tibor (April 1965). "Computerstudien von Turing-Maschinenproblemen" . Zeitschrift der ACM . 12 (2): 196–212. doi : 10.1145/321264.321270 . S2CID 17789208 .
Verweise
-
Radó, Tibor (Mai 1962). "Über nicht berechenbare Funktionen" (PDF) . Bell System Fachzeitschrift . 41 (3): 877–884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
- Hier definierte Radó zum ersten Mal das Busy-Beaver-Problem und bewies, dass es nicht berechenbar ist und schneller gewachsen ist als jede berechenbare Funktion.
-
Lin, Shen; Radó, Tibor (April 1965). "Computerstudien von Turing-Maschinen-Problemen" . Zeitschrift der ACM . 12 (2): 196–212. doi : 10.1145/321264.321270 . S2CID 17789208 .
- Die Ergebnisse dieser Arbeit waren zum Teil bereits in Lins Dissertation 1963 unter der Leitung von Radó erschienen. Lin & Radó beweisen, dass Σ(3) = 6 und S (3) = 21, indem sie beweisen, dass alle 3-Zustands-2-Symbol-Turingmaschinen, die nicht innerhalb von 21 Schritten anhalten, niemals anhalten werden. (Die meisten werden automatisch durch ein Computerprogramm nachgewiesen, 40 jedoch durch menschliche Inspektion.)
-
Brady, Allen H. (April 1983). "Die Bestimmung des Wertes von Rados nicht berechenbarer Funktion Σ( k ) für Turingmaschinen mit vier Zuständen " . Mathematik der Berechnung . 40 (162): 647–665. doi : 10.1090/S0025-5718-1983-0689479-6 . JSTOR 2007539 .
- Brady beweist, dass Σ(4) = 13 und S (4) = 107. Brady definiert zwei neue Kategorien für nicht anhaltende 3-Zustands-2-Symbol-Turing-Maschinen: Weihnachtsbäume und Zähler. Er verwendet ein Computerprogramm, um zu beweisen, dass alle bis auf 27 Maschinen, die über 107 Schritte laufen, Varianten von Weihnachtsbäumen und Zählern sind, die nachweislich unendlich laufen. Die letzten 27 Maschinen (als Holdouts bezeichnet) werden durch persönliche Inspektion von Brady selbst bewiesen, dass sie nicht anhalten.
-
Machlin, Rona; Stout, Quentin F. (Juni 1990). "Das komplexe Verhalten einfacher Maschinen" . Physica D: Nichtlineare Phänomene . 42 (1–3): 85–98. Bibcode : 1990PhyD...42...85M . doi : 10.1016/0167-2789(90)90068-Z . hdl : 2027.42/28528 .
- Machlin und Stout beschreiben das Beschäftigte-Biber-Problem und viele Techniken zum Auffinden von beschäftigten Bibern (die sie auf Turing-Maschinen mit 4 Zuständen und 2 Symbolen anwenden und damit Bradys Beweis verifizieren). Sie schlagen vor, wie man eine Variante der Haltewahrscheinlichkeit von Chaitin (Ω) abschätzt.
-
Marxen, Heiner; Buntrock, Jürgen (Februar 1990). "Angriff auf den fleißigen Biber 5" . Bulletin des EATCS . 40 : 247–251. Archiviert vom Original am 2006-10-09 . Abgerufen 2020-01-19 .
- Marxen und Buntrock zeigen, dass Σ(5) ≥ 4098 und S (5) ≥ 47 176 870 und beschreiben im Detail die Methode, mit der sie diese Maschinen gefunden haben und beweisen, dass viele andere nie aufhören werden.
-
Grün, Milton W. (1964). Eine untere Grenze der Sigma-Funktion von Rado für binäre Turing-Maschinen . 1964 Tagungsband des Fünften Jahressymposiums über Schaltungstheorie und logisches Design . S. 91–94. doi : 10.1109/SWCT.1964.3 .
- Green konstruiert rekursiv Maschinen für eine beliebige Anzahl von Zuständen und stellt die rekursive Funktion bereit, die ihren Score berechnet (berechnet σ), wodurch eine untere Schranke für Σ bereitgestellt wird. Das Wachstum dieser Funktion ist mit dem der Ackermann-Funktion vergleichbar .
-
Dewdney, Alexander K. (1984). „Eine Computerfalle für den fleißigen Biber, die am härtesten arbeitende Turing-Maschine“. Wissenschaftlicher Amerikaner . 251 (2): 10–17.
- Beschäftigte Biber-Programme werden von Alexander Dewdney in Scientific American , August 1984, Seiten 19–23, auch März 1985, S. 3, beschrieben. 23. und April 1985 p. 30 .
- Chaitin, Gregory J. (1987). "Berechnung der Busy Beaver-Funktion" (PDF) . Im Titelbild, TM; Gopinath, B. (Hrsg.). Offene Probleme in Kommunikation und Informatik . Springer. S. 108–112. ISBN 978-0-387-96621-2.
-
Brady, Allen H. (1995). „Das beschäftigte Biberspiel und der Sinn des Lebens“. In Herken, Rolf (Hrsg.). The Universal Turing Machine: A Half-Century Survey (2. Aufl.). Wien, New York: Springer-Verlag. S. 237–254. ISBN 978-3-211-82637-9.
- Worin Brady (von 4-State-Ruhm) einige Geschichte des Tieres beschreibt und seine Verfolgung "The Busy Beaver Game" nennt. Er beschreibt andere Spiele (zB zellulare Automaten und Conways Game of Life ). Von besonderem Interesse ist "The Busy Beaver Game in Two Dimensions" (S. 247). Mit 19 Referenzen.
-
Booth, Taylor L. (1967). Sequentielle Maschinen und Automatentheorie . New York: Wiley. ISBN 978-0-471-08848-6.
- Vgl. Kapitel 9, Turingmaschinen. Ein schwieriges Buch, das für Elektroingenieure und technische Spezialisten gedacht ist. Diskutiert Rekursion, partielle Rekursion mit Bezug auf Turingmaschinen, Halteproblem. Eine Referenz in Booth ordnet Rado beschäftigter Biber zu. Booth definiert auch das Problem des beschäftigten Bibers von Rado in "Heimprobleme" 3, 4, 5, 6 von Kapitel 9, S. 396. Aufgabe 3 besteht darin, "zu zeigen, dass das Busy-Beaver-Problem für alle Werte von n unlösbar ist."
-
Ben-Amram, AM; Julstrom, BA; Zwick, U. (1996). „Eine Anmerkung zu beschäftigten Bibern und anderen Kreaturen“ . Mathematische Systemtheorie . 29 (4): 375–386. CiteSeerX 10.1.1.75.1297 . doi : 10.1007/BF01192693 . S2CID 30937913 .
- Grenzen zwischen den Funktionen Σ und S .
-
Ben-Amram, AM; Petersen, H. (2002). „Verbesserte Grenzen für Funktionen im Zusammenhang mit beschäftigten Bibern“. Theorie der Computersysteme . 35 : 1–11. CiteSeerX 10.1.1.136.5997 . doi : 10.1007/s00224-001-1052-0 . S2CID 10429773 .
- Verbesserte Grenzen.
-
Lafitte, G.; Papazian, C. (Juni 2007). „Das Gewebe der kleinen Turing-Maschinen“. Computation and Logic in the Real World, Proceedings of the Third Conference on Computability in Europe . S. 219–227. CiteSeerX 10.1.1.104.3021 .
- Dieser Artikel enthält eine vollständige Klassifikation der Turingmaschinen mit 2 Zuständen und 3 Symbolen und damit einen Beweis für den (2, 3) beschäftigten Biber: Σ(2, 3) = 9 und S(2, 3) = 38.
- Boolos, George S.; Burgess, John P.; Jeffrey, Richard C. (2007). Berechenbarkeit und Logik (Fünfte Aufl.). Cambridge University Press. ISBN 978-0-521-87752-7.
-
Kropitz, Pavel (2010). Problém Busy Beaver (Bachelorarbeit) (auf Slowakisch). Karlsuniversität in Prag.
- Dies ist die Beschreibung der Ideen, der Algorithmen und ihrer Implementierung, mit der Beschreibung der Experimente, die 5-Zustands- und 6-Zustands-Turingmaschinen durch Parallellauf auf 31 4-Kern-Computern untersuchen und schließlich die besten Ergebnisse für 6-Zustands-TM.
Externe Links
- Die Seite von Heiner Marxen , der zusammen mit Jürgen Buntrock die oben genannten Aufzeichnungen für eine 5- und 6-stufige Turingmaschine gefunden hat.
- Pascal Michels Historischer Überblick über die Ergebnisse von fleißigen Bibern, der auch die besten Ergebnisse und einige Analysen enthält.
- Definition der Klasse RTM - Reversal Turing Machines, einfache und starke Unterklasse der TMs.
- Die „ Millennium Attacke “ im Rensselaer RAIR Lab zum beschäftigten Biber-Problem. Diese Bemühungen fanden mehrere neue Rekorde und ermittelten mehrere Werte für die vierfache Formalisierung.
- Daniel Briggs' Website- Archiv und Forum zur Lösung des 5- State- , 2-Symbol-Busy-Biber-Problems, basierend auf der Liste der nicht regulären Maschinen von Skelet (Georgi Georgiev).
- Aaronson, Scott (1999), Wer kann die größte Zahl nennen?
- Weisstein, Eric W. "Beschäftigter Biber" . MathWorld .
- Busy Beaver Turing-Maschinen - Computerphile
- Pascal Michel. Der Busy Beaver Competition: ein historischer Überblick . 70 Seiten. 2017. <hal-00396880v5>