Gröbner-Basis - Gröbner basis

In der Mathematik und insbesondere in der Computeralgebra , der Computeralgebraischen Geometrie und der Computerkommutativen Algebra ist eine Gröbner-Basis eine besondere Art von Erzeugungsmenge eines Ideals in einem Polynomring K [ x ₁ , …, x _n ] über einem Körper K . Aus einer Gröbner-Basis lassen sich viele wichtige Eigenschaften des Ideals und die zugehörige algebraische Varietät leicht ableiten, wie zum Beispiel die Dimension und die Anzahl der Nullstellen, wenn es endlich ist. Die Gröbner-Basisberechnung ist eines der wichtigsten praktischen Werkzeuge zur Lösung von polynomialen Gleichungssystemen und zur Berechnung der Bilder algebraischer Varietäten unter Projektionen oder rationalen Karten .

Die Berechnung der Gröbner-Basis kann als eine multivariate, nichtlineare Verallgemeinerung sowohl des Euklid-Algorithmus zur Berechnung der polynomialen größten gemeinsamen Teiler als auch der Gaußschen Elimination für lineare Systeme angesehen werden.

Gröbner-Basen wurden 1965 zusammen mit einem Algorithmus zu ihrer Berechnung ( Buchberger-Algorithmus ) von Bruno Buchberger in seinem Ph.D. These. Er benannte sie nach seinem Berater Wolfgang Gröbner . Im Jahr 2007 erhielt die Buchberger Association for Computing Machinery ‚s Paris Kanellakis Theorie und Praxis Auszeichnung für diese Arbeit. Der russische Mathematiker Nikolai Günther hatte jedoch 1913 einen ähnlichen Begriff eingeführt, der in verschiedenen russischen mathematischen Zeitschriften veröffentlicht wurde. Diese Arbeiten wurden von der mathematischen Gemeinschaft bis zu ihrer Wiederentdeckung 1987 durch Bodo Renschuch et al. weitgehend ignoriert . Ein analoges Konzept für multivariate Potenzreihen wurde 1964 unabhängig von Heisuke Hironaka entwickelt , der sie als Standardbasen bezeichnete . Dieser Begriff wurde von einigen Autoren auch verwendet, um Gröbner-Basen zu bezeichnen.

Die Theorie der Gröbnerbasen wurde von vielen Autoren in verschiedene Richtungen erweitert. Es wurde auf andere Strukturen wie Polynome über idealen Hauptringen oder Polynomringen verallgemeinert , und auch auf einige Klassen nichtkommutativer Ringe und Algebren, wie Ore-Algebren .

Hintergrund

Polynomring

Gröbnerbasen werden hauptsächlich für Ideale in einem Polynomring über einem Körper K definiert . Obwohl die Theorie für jeden Körper funktioniert, werden die meisten Berechnungen mit Gröbner-Basis entweder durchgeführt, wenn K der Körper der rationalen Zahlen oder die ganzen Zahlen modulo einer Primzahl sind. ${\displaystyle R=K[x_{1},\ldots,x_{n}]}$

Ein Polynom ist eine Summe , wo die Nicht - Null - Elemente sind K und das sind Monomen oder „Power - Produkte“ der Variablen. Dies bedeutet, dass ein Monom M ein Produkt ist, bei dem es sich um nichtnegative ganze Zahlen handelt. Der Vektor heißt Exponentenvektor von M . Die Notation wird oft abgekürzt als . Monome sind eindeutig durch ihre Exponentenvektoren definiert, sodass Computer Monome effizient als Exponentenvektoren und Polynome als Listen von Exponentenvektoren und ihren Koeffizienten darstellen können. ${\displaystyle c_{1}M_{1}+\cdots +c_{m}M_{m}}$${\displaystyle c_{i}}$${\displaystyle M_{i}}$${\displaystyle M=x_{1}^{a_{1}}\cdots x_{n}^{a_{n}},}$${\displaystyle a_{i}}$${\displaystyle A=[a_{1},\ldots ,a_{n}]}$${\displaystyle x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}=X^{A}}$

Wenn eine endliche Menge von Polynomen in einem Polynomring R ist , ist das von F erzeugte Ideal die Menge von Linearkombinationen von Elementen aus F mit Koeffizienten in ganz R : ${\displaystyle F=\{f_{1},\ldots,f_{k}\}}$

${\displaystyle \langle f_{1},\ldots,f_{k}\rangle =\left\{\sum_{i=1}^{k}g_{i}f_{i}\mid g_{1} ,\ldots ,g_{k}\in K[x_{1},\ldots ,x_{n}]\right\}.}$

Monomische Bestellung

Alle Vorgänge im Zusammenhang mit Gröbner Basen erfordern die Wahl eines Gesamtauftrages auf den Monomen, mit den folgenden Eigenschaften der Kompatibilität mit der Multiplikation. Für alle Monome M , N , P ,

1. ${\displaystyle M\leq N\Longleftrightarrow MP\leq NP}$
2. ${\displaystyle M\leq MP}$.

Eine Gesamtbestellung, die diese Bedingung erfüllt, wird manchmal als zulässige Bestellung bezeichnet .

Diese Bedingungen implizieren, dass die Ordnung eine Wohlordnung ist , d. h. jede streng abnehmende Folge von Monomen ist endlich.

Obwohl die Gröbner-Basistheorie nicht von einer bestimmten Wahl einer zulässigen Monomordnung abhängt, sind drei Monomordnungen für die Anwendungen besonders wichtig:

• Lexikographische Ordnung , allgemein Lex oder Plex genannt (für reine lexikalische Ordnung).
• Gesamtgrad umgekehrte lexikographische Ordnung , allgemein als Degrevlex bezeichnet .
• Eliminationsordnung , lexdeg .

Für die lexikographische Ordnung wurde zunächst die Gröbner-Basistheorie eingeführt. Es wurde schnell erkannt, dass die Gröbner-Basis für Degrevlex fast immer viel einfacher zu berechnen ist und dass es fast immer einfacher ist, eine lex-Gröbner-Basis zu berechnen, indem zuerst die Degrevlex-Basis berechnet und dann ein "Orderänderungsalgorithmus" verwendet wird. Wenn eine Elimination erforderlich ist, ist Degrevlex nicht geeignet; sowohl lex als auch lexdeg können verwendet werden, aber auch hier sind viele Berechnungen mit lexdeg relativ einfach und mit lex fast unmöglich.

Sobald eine Monomordnung festgelegt ist, werden die Terme eines Polynoms (Produkt eines Monoms mit seinem Koeffizienten ungleich Null) natürlich durch abnehmende Monome (für diese Ordnung) geordnet. Dies macht die Darstellung eines Polynoms als geordnete Liste von Paaren Koeffizient-Exponent-Vektor zu einer kanonischen Darstellung der Polynome. Die erste ( am höchsten) , Laufzeit eines Polynoms p für diese Anordnung und die entsprechende Monom und Koeffizienten jeweils die genannte Leitterm , führenden Monom und Leitkoeffizient und bezeichnet in diesem Artikel lt ( p ), lm ( p ) und LC ( p ).

Die Ermäßigung

Das Konzept der Reduktion , auch multivariate Division oder Normalformberechnung genannt , ist von zentraler Bedeutung für die Gröbner-Basistheorie. Es ist eine multivariate Verallgemeinerung der euklidischen Division von univariaten Polynomen .

In diesem Abschnitt nehmen wir eine feste monomische Ordnung an, die nicht explizit definiert wird.

Sind zwei Polynome f und g , sagt man , dass f ist reduzierbaren durch g , wenn einige Monom m in f ein Mehrfaches der führenden Monom lm (ist g ) von g . Wenn m die führende monomial von sein geschieht f dann sagt man , dass f ist blei reduzierbar durch g . Wenn c der Koeffizient von m in f und m = q lm( g ) ist, ist die einstufige Reduktion von f um g die Operation, die f das Polynom

${\displaystyle \operatorname {red} _{1}(f,g)=f-{\frac {c}{\operatorname {lc} (g)}}\,q\,g.}$

Die Haupteigenschaften dieser Operation sind, dass das resultierende Polynom das Monom m nicht enthält und dass die Monome größer als m (für die Monomordnung) unverändert bleiben. Diese Operation ist im Allgemeinen nicht eindeutig definiert; wenn mehrere Monome in f Vielfache von lm( g ) sind, dann kann man beliebig wählen, welches zu reduzieren ist. In der Praxis ist es besser, das Größte für die Monomordnung zu wählen, da sonst nachfolgende Reduktionen das gerade entfernte Monom wieder einführen könnten.

Eine endliche Menge gegeben G von Polynomen, sagt man , dass f ist reduzierbar oder Blei-reduzierbaren von G , wenn sie reduzierbare oder Blei-reduzierbar ist, die jeweils von einem Element g von G . Ist dies der Fall, so definiert man . Die (vollständige) Reduktion von f um G besteht darin, diesen Operator iterativ anzuwenden, bis ein Polynom erhalten wird , das durch G irreduzibel ist . Sie heißt Normalform von f nach G . Im Allgemeinen ist diese Form nicht eindeutig definiert (dies ist keine kanonische Form ); diese Nichteindeutigkeit ist der Ausgangspunkt der Gröbner-Basistheorie. ${\displaystyle \operatorname {red} _{1}(f,G)=\operatorname {red} _{1}(f,g)}$${\displaystyle \operatorname {red} _{1}}$${\displaystyle \operatorname {red} (f,G)}$

Bei Gröbner-Basisberechnungen ist außer am Ende keine vollständige Reduktion erforderlich: eine Bleireduktion ist ausreichend, was viel Rechenaufwand einspart.

Die Definition der Reduktion zeigt sofort, dass wenn h eine Normalform von f nach G ist , dann gilt

${\displaystyle f=h+\sum_{g\in G}q_{g}\,g,}$

wobei die Polynome sind. Im Fall von univariaten Polynomen, wenn G aus einem einzigen Element g besteht , dann ist h der Rest der euklidischen Division von f durch g , q _g ist der Quotient und der Divisionsalgorithmus ist genau der Prozess der Bleireduktion. Aus diesem Grund verwenden einige Autoren den Begriff multivariate Division anstelle von Reduktion. ${\displaystyle q_{g}}$

Reduktionsbeispiele

In den Beispielen dieses Abschnitts haben die drei Polynome indeterminates x , y und z und die Monom Ordnung , die verwendet wird , ist das Monom um mit das heißt, für den Vergleich von zwei Monome, die einen ersten Exponenten vergleicht x ; nur wenn die Exponenten von x gleich sind, vergleicht man die Exponenten von y ; und die Exponenten von z werden nur verglichen, wenn die anderen Exponenten gleich sind. ${\displaystyle x\succ y\succ z;}$

Um einen klaren Überblick über den Reduktionsprozess zu haben, muss man Polynome mit ihren Termen in absteigender Reihenfolge umschreiben. Zum Beispiel, wenn

${\displaystyle P=xy^{3}z^{5}+x^{2}y^{6}+x^{4}yz+y^{2}z^{5}+yz^{4} +y^{3}+z^{3}+xy+xz+z^{2}+z,}$

es muss umgeschrieben werden

${\displaystyle P=x^{4}yz+x^{2}y^{6}+xy^{3}z^{5}+xy+xz+y^{3}+y^{2}z ^{5}+yz^{4}+z^{3}+z^{2}+z.}$

Dies ermöglicht es, das führende Monom zuerst zu haben (für die gewählte Ordnung); Hier${\displaystyle \operatorname {lm} (P)=x^{4}yz.}$

Betrachten Sie die Reduktion von um mit und${\displaystyle f=2x^{3}-x^{2}y+y^{3}+3y\;}$${\displaystyle \;G=\{g_{1},g_{2}\},}$${\displaystyle g_{1}=x^{2}+y^{2}-1}$${\displaystyle g_{2}=xy-2.}$

Für den ersten Reduktionsschritt kann entweder der erste oder der zweite Term reduziert werden. Die Reduzierung eines Termes führt jedoch dazu, dass dieser Term auf Kosten des Hinzufügens neuer niedrigerer Terme entfernt wird, und wenn nicht der erste reduzierbare Term reduziert wird, ist es möglich, dass eine weitere Reduzierung einen ähnlichen Term hinzufügt, der wieder reduziert. Es ist daher immer besser, zuerst den größten (für die monomische Ordnung) reduzierbaren Term zu reduzieren.

Der führende Term von f ist reduzierbar durch Der erste Reduktionsschritt besteht also darin, mit –2 x zu multiplizieren und das Ergebnis zu f zu addieren : ${\displaystyle 2x^{3}}$${\displaystyle g_{1}.}$${\displaystyle g_{1}}$

${\displaystyle f\;{\overset {-2xg_{1}}{\longrightarrow}}\;f_{1}=f-2xg_{1}=-x^{2}y-2xy^{2}+2x +j^{3}+3j.}$

Als führende Term der ein Vielfaches der führenden Monome von beiden und hat zwei Wahlmöglichkeiten für die zweite Reduktionsstufe. Wählt man, erhält man ein Polynom, das wieder um . reduziert werden kann${\displaystyle -x^{2}y}$${\displaystyle f_{1}}$${\displaystyle g_{1}}$${\displaystyle g_{2},}$${\displaystyle g_{2},}$${\displaystyle g_{2}\colon }$

${\displaystyle f\;{\overset {-2xg_{1}}{\longrightarrow}}\;f_{1}\;{\overset {xg_{2}}{\longrightarrow}}\;-2xy^{2 }+y^{3}+3y\;{\overset {2yg_{2}}{\longrightarrow}}\;f_{2}=+y^{3}-y.}$

Es ist keine weitere Reduktion möglich, kann also für die vollständige Reduktion von f gewählt werden . Mit der anderen Wahl für den zweiten Schritt erhält man jedoch ein anderes Ergebnis: ${\displaystyle f_{2}}$

${\displaystyle f\;{\overset {-2xg_{1}}{\longrightarrow}}\;f_{1}\;{\overset {yg_{1}}{\longrightarrow}}\;-2xy^{2 }+2x+2y^{3}+2y\;{\overset {2yg_{2}}{\longrightarrow}}\;f_{3}=+2x+2y^{3}-2y.}$

Daher kann die vollständige Reduktion von f entweder oder${\displaystyle f_{2}}$${\displaystyle f_{3}.}$

Der Algorithmus von Buchberger wurde eingeführt, um die durch diese Nichteindeutigkeit verursachten Schwierigkeiten zu lösen. Grob gesagt besteht sie darin, zu G die Polynome hinzuzufügen, die für die Eindeutigkeit der Reduktion um G benötigt werden .

Hier würde Buchbergers Algorithmus damit beginnen, dass zu G das Polynom

${\displaystyle g_{3}=yg_{1}-xg_{2}=2x+y^{3}-y.}$

In der Tat kann dadurch weiter reduziert werden und dies wieder hergestellt werden. Dies vervollständigt den Buchberger-Algorithmus jedoch nicht, da xy bei Reduktion um oder . andere Ergebnisse liefert${\displaystyle f_{3}}$${\displaystyle g_{3},}$${\displaystyle f_{2}}$${\displaystyle g_{2}}$${\displaystyle g_{3}.}$

Formale Definition

Eine Gröbner-Basis G eines Ideals I in einem Polynomring R über einem Körper ist ein erzeugender Satz von I , der durch eine der folgenden Eigenschaften, relativ zu einer monomialen Ordnung, gekennzeichnet ist :

• das von den führenden Termen von Polynomen in I erzeugte Ideal ist gleich dem von den führenden Termen von G erzeugten Ideal ;
• der führende Term eines Polynoms in I ist durch den führenden Term eines Polynoms in G teilbar ;
• die multivariate Division eines beliebigen Polynoms im Polynomring R durch G ergibt einen eindeutigen Rest;
• die multivariate Division durch G eines beliebigen Polynoms im Ideal I ergibt den Rest 0 .

Alle diese Eigenschaften sind gleichwertig; verschiedene Autoren verwenden je nach gewähltem Thema unterschiedliche Definitionen. Die letzten beiden Eigenschaften erlauben Berechnungen im Faktorring R/I mit der gleichen Leichtigkeit wie die modulare Arithmetik. Es ist eine wesentliche Tatsache der kommutativen Algebra, dass Gröbner-Basen immer existieren und effektiv für jedes Ideal berechnet werden können, das durch eine endliche erzeugende Teilmenge gegeben ist.

Die multivariate Division erfordert eine monomische Ordnung, die Basis hängt von der gewählten monomischen Ordnung ab, und unterschiedliche Ordnungen können zu radikal unterschiedlichen Gröbner-Basen führen. Zwei der am häufigsten verwendeten Anordnungen sind lexikographische Ordnung und Grad umgekehrte lexikographische Ordnung (auch genannt abgestuft Reverse lexicographic Ordnung oder einfach Gesamt Grad Ordnung ). Die lexikographische Ordnung eliminiert Variablen, jedoch sind die resultierenden Gröbner-Basen oft sehr groß und teuer zu berechnen. Die umgekehrte lexikografische Ordnung des Grades liefert typischerweise die schnellsten Berechnungen auf der Gröbner-Basis. In dieser Reihenfolge werden die Monome zuerst nach dem Gesamtgrad verglichen, wobei die Bindungen unterbrochen werden, indem das kleinste Monom in Bezug auf die lexikographische Ordnung mit den umgekehrten Variablen genommen wird.

In den meisten Fällen (Polynome in endlich vielen Variablen mit komplexen Koeffizienten oder allgemeiner Koeffizienten über einem beliebigen Körper, zum Beispiel) existieren Gröbner-Basen für jede monomische Ordnung. Der Algorithmus von Buchberger ist die älteste und bekannteste Methode, sie zu berechnen. Andere Methoden sind die F4- und F5-Algorithmen von Faugère , die auf derselben Mathematik wie der Buchberger-Algorithmus basieren, und involutive Ansätze, die auf Ideen der Differentialalgebra basieren . Es gibt auch drei Algorithmen zum Umwandeln einer Gröbner-Basis bezüglich einer Monomordnung in eine Gröbner-Basis bezüglich einer anderen Monomordnung: den FGLM-Algorithmus , den Hilbert-getriebenen Algorithmus und den Gröbner-Walk-Algorithmus . Diese Algorithmen werden oft verwendet, um (schwierige) lexikographische Gröbner-Basen aus (einfacheren) Gröbner-Basen mit Gesamtgrad zu berechnen.

Eine Gröbner-Basis wird als reduziert bezeichnet, wenn der führende Koeffizient jedes Elements der Basis 1 ist und kein Monom in irgendeinem Element der Basis im Ideal vorhanden ist, das von den führenden Termen der anderen Elemente der Basis erzeugt wird. Im schlimmsten Fall kann die Berechnung einer Gröbner-Basis eine exponentielle oder sogar doppelt exponentielle Zeit in der Anzahl der Lösungen des Polynomsystems erfordern (für Grad umgekehrte lexikographische Ordnung bzw. lexikographische Ordnung). Trotz dieser Komplexitätsgrenzen sind sowohl Standard- als auch reduzierte Gröbner-Basen in der Praxis oft berechenbar, und die meisten Computeralgebra-Systeme enthalten dazu Routinen.

Das Konzept und die Algorithmen der Gröbner-Basen wurden auf Untermodule von freien Modulen über einem Polynomring verallgemeinert . Wenn L ein freies Modul über einem Ring R ist , dann kann man R ⊕ L als Ring betrachten, indem man das Produkt zweier Elemente von L als 0 definiert. Dieser Ring kann identifiziert werden mit , wobei eine Basis von L . ist . Dies erlaubt es, ein Untermodul von L erzeugt von mit dem Ideal von erzeugt von und den Produkten , zu identifizieren . Wenn R ein Polynomring ist, reduziert dies die Theorie und die Algorithmen der Gröbner-Grundlagen der Module auf die Theorie und die Algorithmen der Gröbner-Grundlagen der Ideale. ${\displaystyle R[e_{1},\ldots,e_{l}]/\left\langle \{e_{i}e_{j}|1\leq i\leq j\leq l\}\right\rangle }$${\displaystyle e_{1},\ldots ,e_{l}}$${\displaystyle g_{1},\ldots,g_{k}}$${\displaystyle R[e_{1},\ldots,e_{l}]}$${\displaystyle g_{1},\ldots,g_{k}}$${\displaystyle e_{i}e_{j}}$${\displaystyle 1\leq i\leq j\leq l}$

Das Konzept und die Algorithmen der Gröbner-Basen wurden auch auf Ideale über verschiedene Ringe verallgemeinert, kommutativ oder nicht, wie Polynomringe über einem idealen Hauptring oder Weyl-Algebren .

Beispiel und Gegenbeispiel

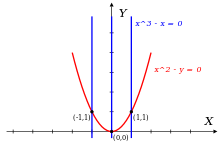
Sei der Ring bivariater Polynome mit rationalen Koeffizienten und betrachte das von den Polynomen erzeugte Ideal${\displaystyle R=\mathbb{Q} [x,y]}$${\displaystyle I=\langle f,g\rangle}$

${\displaystyle f(x,y)=x^{2}-y}$,

${\displaystyle g(x,y)=x^{3}-x}$.

Zwei weitere Elemente von I sind die Polynome

k ( x , y ) = − xf ( x , y ) + g ( x , y ) = xy − x

h ( x , y ) = xk ( x , y ) − ( y - 1) f ( x , y ) = y ² − y

Unter lexikographischer Ordnung mit haben wir ${\displaystyle x>y}$

lt( f ) = x ²

lt( g ) = x ³

lt( h ) = y ²

Das von {lt( f ),lt( g )} erzeugte Ideal enthält nur Polynome, die durch x ² teilbar sind, was lt( h ) = y ^{2 ausschließt} ; folgt, dass { f , g } keine Gröbner-Basis für I ist.

Andererseits können wir zeigen, dass { f , k , h } tatsächlich eine Gröbner-Basis für I ist.

Zum einen haben f und g und damit auch h, k und alle anderen Polynome im Ideal I die folgenden drei Nullstellen in der ( x , y )-Ebene gemeinsam, wie in der Abbildung angedeutet: {(1,1), (−1,1),(0,0)}. Diese drei Punkte sind nicht kollinear, daher enthält I kein Polynom ersten Grades. Ich kann auch keine Polynome der Sonderform

m ( x , y ) = cx + p ( y )

mit c eine rationale Zahl ungleich Null und p ein Polynom nur in der Variablen y ; der Grund dafür ist, dass ein solches m niemals zwei verschiedene Nullen mit dem gleichen Wert für y haben kann (in diesem Fall die Punkte (1,1) und (−1,1)).

Aus dem Obigen folgt, dass I außer dem Nullpolynom nur Polynome enthält, deren führender Term einen Grad größer oder gleich 2 hat; daher sind ihre führenden Terme durch mindestens eines der drei Monome teilbar

{ X ² , xy , y ² } = {lt ( f ), LT ( k ), LT ( h )}.

Dies bedeutet, dass { f , k , h } eine Gröbner-Basis für I bezüglich der lexikographischen Ordnung mit x > y ist.

Eigenschaften und Anwendungen von Gröbner-Basen

Sofern nicht ausdrücklich angegeben, gelten alle folgenden Ergebnisse für jede monomische Ordnung (siehe diesen Artikel für die Definitionen der verschiedenen Ordnungen, die unten erwähnt werden).

Es ist ein weit verbreiteter Irrglaube, dass für einige dieser Ergebnisse die lexikographische Reihenfolge benötigt wird. Im Gegenteil, die lexikographische Ordnung ist fast immer am schwierigsten zu berechnen, und ihre Verwendung macht viele Berechnungen unpraktisch, die mit abgestufter umgekehrter lexikographischer Ordnung (grevlex) oder, wenn eine Elimination erforderlich ist, der Eliminationsordnung (lexdeg ), die sich auf Grevlex für jeden Variablenblock beschränkt.

Gleichheit der Ideale

Reduzierte Gröbner-Basen sind einzigartig für jedes gegebene Ideal und jede monomische Ordnung. Somit sind zwei Ideale genau dann gleich, wenn sie dieselbe (reduzierte) Gröbner-Basis haben (normalerweise erzeugt eine Gröbner-Basis-Software immer reduzierte Gröbner-Basen).

Mitgliedschaft und Einbeziehung von Idealen

Die Reduktion eines Polynoms f um die Gröbner-Basis G eines Ideals I liefert 0 genau dann, wenn f in I ist . Dies ermöglicht es, die Zugehörigkeit eines Elements zu einem Ideal zu testen. Eine andere Methode besteht darin, zu verifizieren, dass die Gröbner-Basis von G ∪{ f } gleich G ist .

Um zu testen, ob das von f ₁ , …,  f _k erzeugte Ideal I im Ideal J enthalten ist , genügt es zu testen, dass jedes f _i in J ist . Man kann auch die Gleichheit der reduzierten Gröbnerbasen von J und J  ∪ { f ₁ , ..., f _k } testen .

Lösungen eines Systems algebraischer Gleichungen

Jeder Satz von Polynomen kann als ein System von Polynomgleichungen angesehen werden, indem die Polynome mit Null gleichgesetzt werden. Die Menge der Lösungen eines solchen Systems hängt nur vom erzeugten Ideal ab und ändert sich daher nicht, wenn der gegebene erzeugende Satz bei beliebiger Ordnung durch die Gröbner-Basis des erzeugten Ideals ersetzt wird. Eine solche Lösung mit Koordinaten in einem algebraisch abgeschlossenen Körper , der die Koeffizienten der Polynome enthält, wird als Nullstelle des Ideals bezeichnet . Im üblichen Fall rationaler Koeffizienten wird dieser algebraisch abgeschlossene Körper als komplexer Körper gewählt .

Ein Ideal hat keine Nullstelle (das Gleichungssystem ist inkonsistent ) genau dann, wenn 1 zum Ideal gehört (das ist Hilberts Nullstellensatz ), oder äquivalent seine Gröbner-Basis (für jede monomische Ordnung) 1 enthält, oder, auch, wenn die entsprechende reduzierte Gröbner-Basis [1] ist.

Angesichts der Gröbner Basis G einer idealen I , es nur eine endliche Anzahl von Nullen hat, wenn , und nur wenn, für jede Variable x , G ein Polynom mit einem führenden Monom enthält , die eine Zweierpotenz ist , x (ohne irgendeine andere Variable erscheint in der führende Begriff). Wenn dies der Fall ist, ist die Anzahl der Nullen, mit Multiplizität gezählt, gleich der Anzahl der Monome, die kein Vielfaches eines führenden Monoms von G sind . Diese Zahl wird als Grad des Ideals bezeichnet.

Wenn die Anzahl der Nullstellen endlich ist, liefert die Gröbner-Basis für eine lexikographische Monomordnung theoretisch eine Lösung: Die ersten Koordinaten einer Lösung sind eine Wurzel des größten gemeinsamen Teilers der Basispolynome, der nur von der ersten Variablen abhängt. Nach dem Einsetzen dieser Wurzel in die Basis sind die zweiten Koordinaten dieser Lösung eine Wurzel des größten gemeinsamen Teilers der resultierenden Polynome, die nur von dieser zweiten Variablen abhängt, und so weiter. Dieser Lösungsprozess ist nur theoretisch, da er GCD-Berechnung und Wurzelfindung von Polynomen mit angenäherten Koeffizienten impliziert, die wegen numerischer Instabilität nicht praktikabel sind. Daher wurden andere Methoden entwickelt, um polynomiale Systeme durch Gröbner-Basen zu lösen (siehe System polynomialer Gleichungen für weitere Details).

Dimension, Grad und Hilbert-Reihe

Die Dimension eines idealen I in einem Polynomring R ist die Krull-Dimension des Rings R / I und gleich der Dimension der algebraischen Menge der Nullstellen von I . Es ist auch gleich der Anzahl der Hyperebenen in allgemeiner Position, die benötigt werden, um einen Schnittpunkt mit der algebraischen Menge zu haben, die eine endliche Anzahl von Punkten ist. Der Grad des Ideals und seiner zugehörigen algebraischen Menge ist die Anzahl der Punkte dieses endlichen Schnitts, gezählt mit Vielfachheit. Insbesondere ist der Grad einer Hyperfläche gleich dem Grad ihres Definitionspolynoms.

Sowohl Grad als auch Dimension hängen für jede Monomordnung nur von der Menge der führenden Monome der Gröbner-Basis des Ideals ab.

Die Dimension ist die maximale Größe einer Teilmenge S der Variablen, so dass es kein führendes Monom gibt, das nur von den Variablen in S abhängt . Wenn also das Ideal die Dimension 0 hat, dann gibt es für jede Variable x ein führendes Monom in der Gröbner-Basis, das eine Potenz von x ist .

Sowohl Dimension als auch Grad können aus der Hilbert-Reihe des Ideals abgeleitet werden, die die Reihe ist , wobei die Anzahl der Monome vom Grad i ist , die kein Vielfaches eines führenden Monoms in der Gröbner-Basis sind. Die Hilbert-Reihe kann zu einem rationalen Bruch summiert werden ${\textstyle \sum _{i=0}^{\infty}d_{i}t^{i}}$${\displaystyle d_{i}}$

${\displaystyle \sum _{i=0}^{\infty}d_{i}t^{i}={\frac {P(t)}{(1-t)^{d}}},}$

wobei d die Dimension des Ideals und ein Polynom ist, das den Grad des Ideals darstellt. ${\displaystyle P(t)}$${\displaystyle P(1)}$

Obwohl die Dimension und der Grad nicht von der Wahl der monomischen Ordnung abhängen, ändern sich die Hilbert-Reihe und das Polynom , wenn man die monomiale Ordnung ändert. ${\displaystyle P(t)}$

Die meisten Computeralgebrasysteme , die Funktionen zur Berechnung von Gröbner-Basen bereitstellen, bieten auch Funktionen zur Berechnung der Hilbert-Reihe und damit auch der Dimension und des Grades.

Beseitigung

Die Berechnung von Gröbner-Basen für eine Eliminationsmonom- Ordnung ermöglicht eine rechnerische Eliminationstheorie . Dies basiert auf dem folgenden Satz.

Betrachten Sie einen Polynomring, in dem die Variablen in zwei Teilmengen X und Y aufgeteilt sind . Wählen wir auch eine Eliminationsmonom-Ordnung, die X "eliminiert" , d. h. eine Monom-Ordnung, bei der zwei Monome verglichen werden, indem zuerst die X- Anteile verglichen werden und nur im Falle der Gleichheit die Y- Anteile berücksichtigt werden. Dies impliziert, dass ein Monom, das eine X- Variable enthält, größer ist als jedes von X unabhängige Monom . Wenn G eine Gröbner-Basis eines Ideals I für diese monomische Ordnung ist, dann ist es eine Gröbner-Basis von (dieses Ideal wird oft als Eliminationsideal bezeichnet ). Darüber hinaus besteht genau die Polynome von G , deren führenden Begriffen gehören zu K [ Y ] (das macht sehr einfach , die Berechnung , da nur die führenden Monome müssen überprüft werden). ${\displaystyle K[x_{1},\ldots,x_{n},y_{1},\ldots,y_{m}]=K[X,Y],}$${\displaystyle G\cap K[Y]}$${\displaystyle I\cap K[Y]}$${\displaystyle G\cap K[Y]}$${\displaystyle G\cap K[Y]}$

Diese Eliminationseigenschaft hat viele Anwendungen, von denen einige in den nächsten Abschnitten beschrieben werden.

Eine andere Anwendung in der algebraischen Geometrie besteht darin , dass die Eliminierung die geometrische Operation der Projektion einer affinen algebraischen Menge in einen Unterraum des Umgebungsraums realisiert: mit obiger Notation die ( Zariski-Abschluss von) die Projektion der algebraischen Menge, die durch das ideale I . definiert wird in den Y -Unterraum ist definiert durch das Ideal${\displaystyle I\cap K[Y].}$

Die lexikographische Ordnung, also eine Eliminationsordnung für jede Partition. Somit trägt eine Gröbner-Basis für diese Ordnung viel mehr Informationen als normalerweise notwendig. Dies mag erklären, warum Gröbner-Basen für die lexikographische Ordnung in der Regel am schwierigsten zu berechnen sind. ${\displaystyle x_{1}>\cdots >x_{n}}$${\displaystyle \{x_{1},\ldots,x_{k}\},\{x_{k+1},\ldots,x_{n}\}.}$

Sich überschneidende Ideale

Wenn I und J zwei Ideale sind, die jeweils durch { f ₁ , ..., f _m } und { g ₁ , ..., g _k } erzeugt werden, dann erzeugt eine einzelne Gröbner-Basisberechnung eine Gröbner-Basis ihres Schnitts I  ∩  J . Dazu führt man ein neues unbestimmtes t ein , und man verwendet eine Eliminationsreihenfolge, so dass der erste Block nur t enthält und der andere Block alle anderen Variablen enthält (das bedeutet, dass ein Monom, das t enthält, größer ist als jedes Monom, das nicht enthält t ). Bei dieser monomialen Ordnung besteht eine Gröbner-Basis von I  ∩  J in den Polynomen, die t nicht enthalten , in der Gröbner-Basis des Ideals

${\displaystyle K=\langle tf_{1},\ldots,tf_{m},(1-t)g_{1},\ldots,(1-t)g_{k}\rangle.}$

Mit anderen Worten, I  ∩  J wird durch Eliminieren von t in K erhalten . Dies kann durch die Bemerkung nachgewiesen werden , dass die ideale K in den Polynomen besteht , so dass und . Ein solches Polynom ist genau dann unabhängig von t a = b , was bedeutet, dass${\displaystyle (ab)t+b}$${\displaystyle a\in I}$${\displaystyle b\in J}$${\displaystyle b\in I\cap J.}$

Implizitation einer rationalen Kurve

Eine rationale Kurve ist eine algebraische Kurve mit einer parametrischen Gleichung der Form

${\displaystyle {\begin{aligned}x_{1}&={\frac {f_{1}(t)}{g_{1}(t)}}\\&\;\;\vdots \\x_{ n}&={\frac {f_{n}(t)}{g_{n}(t)}},\end{ausgerichtet}}}$

wobei und univariate Polynome für 1 ≤ i ≤ n sind . Man kann (und wird) annehmen , dass und sind coprime (sie haben keine nicht-ständige gemeinsame Faktoren). ${\displaystyle f_{i}(t)}$${\displaystyle g_{i}(t)}$${\displaystyle f_{i}(t)}$${\displaystyle g_{i}(t)}$

Implizitisierung besteht darin, die impliziten Gleichungen einer solchen Kurve zu berechnen . Im Fall von n = 2, also bei ebenen Kurven, kann dies mit der Resultierenden berechnet werden . Die implizite Gleichung ist die folgende Resultierende:

${\displaystyle {\text{Res}}_{t}(g_{1}x_{1}-f_{1},g_{2}x_{2}-f_{2}).}$

Elimination mit Gröbner-Basen erlaubt es, für jeden Wert von n zu implizitieren , indem man einfach t im Ideal eliminiert. Wenn n = 2, ist das Ergebnis das gleiche wie bei der Resultierenden, wenn die Abbildung für fast jedes t injektiv ist . Im anderen Fall ist die Resultierende eine Potenz des Ergebnisses der Eliminierung. ${\displaystyle \langle g_{1}x_{1}-f_{1},\ldots,g_{n}x_{n}-f_{n}\rangle.}$${\displaystyle t\mapsto (x_{1},x_{2})}$

Sättigung

Bei der Modellierung eines Problems durch Polynomgleichungen kommt es sehr häufig vor, dass einige Größen ungleich Null sein sollen, denn wenn sie Null sind, wird das Problem ganz anders. Beim Umgang mit Dreiecken werden beispielsweise viele Eigenschaften falsch, wenn das Dreieck entartet ist, dh wenn die Länge einer Seite gleich der Summe der Längen der anderen Seiten ist. In solchen Situationen besteht keine Hoffnung, relevante Informationen aus dem Polynomsystem abzuleiten, wenn die entarteten Lösungen nicht herausfallen. Genauer gesagt definiert das Gleichungssystem eine algebraische Menge, die mehrere irreduzible Komponenten haben kann , und man muss die Komponenten entfernen, bei denen die Entartungsbedingungen überall Null sind.

Dies geschieht durch Sättigung der Gleichungen durch die Entartungsbedingungen, was durch Ausnutzung der Eliminationseigenschaft von Gröbner-Basen erfolgen kann.

Definition der Sättigung

Die Lokalisierung eines Ringes besteht darin, die formalen Inversen einiger Elemente an ihn anzuhängen. Dieser Abschnitt betrifft nur den Fall eines einzelnen Elements oder äquivalent einer endlichen Anzahl von Elementen (das Angrenzen der Inversen mehrerer Elemente entspricht dem Angrenzen der Inversen ihres Produkts). Die Lokalisierung eines Rings R durch ein Element f ist der Ring, wobei t eine neue Unbestimmte ist, die die Inverse von f repräsentiert . Die Lokalisierung eines Ideals I von R ist das Ideal von Wenn R ein Polynomring ist, ist die Berechnung nicht effizient, da die Nenner verwaltet werden müssen. Daher wird der Vorgang der Lokalisierung normalerweise durch den Vorgang der Sättigung ersetzt . ${\displaystyle R_{f}=R[t]/(1-ft),}$${\displaystyle R_{f}I}$${\displaystyle R_{f}.}$${\displaystyle R_{f}}$

Die Sättigung bezüglichfeines IdealsIinRist das inverse Bild vonunter der kanonischen Abbildung vonRnachEs ist das Ideal, dasaus allen Elementen vonR besteht,deren Produkte mit einer Potenz vonfzuI gehören. ${\displaystyle R_{f}I}$${\displaystyle R_{f}.}$${\displaystyle I:f^{\infty}=\{g\in R|(\exists k\in\mathbb{N} )f^{k}g\in I\}}$

Wenn J das von I erzeugte Ideal und 1- ft in R [ t ] ist, dann folgt, dass, wenn R ein Polynomring ist, eine Gröbner-Basisberechnung unter Eliminierung von t die Berechnung einer Gröbner-Basis der Sättigung eines Ideals durch a Polynom. ${\displaystyle I:f^{\infty}=J\cap R.}$

Die wichtige Eigenschaft der Sättigung, die dafür sorgt, dass sie aus der durch das Ideal I definierten algebraischen Menge die irreduziblen Komponenten entfernt, auf denen das Polynom f null ist, ist folgende: Die Primärzerlegung von besteht aus den Komponenten der Primärzerlegung von I die keine Potenz von f enthalten . ${\displaystyle I:f^{\infty}}$

Berechnung der Sättigung

A Gröbner Basis der Sättigung durch F eines durch eine endliche Menge von Polynomen erzeugten Polynom ideal F kann durch Eliminierung erhalten werden t in dass , indem die Polynome unabhängig davon ist , t in der Basis Gröbner für eine Eliminierungs Ordnung eliminiert t . ${\displaystyle F\cup \{1-tf\},}$${\displaystyle F\cup \{1-tf\}}$

Anstelle von F kann man auch von einer Gröbner-Basis von F ausgehen . Welche Methode am effizientesten ist, hängt vom Problem ab. Wenn die Sättigung jedoch keine Komponente entfernt, dh wenn das Ideal gleich seinem gesättigten Ideal ist, ist die Berechnung zuerst der Gröbner-Basis von F normalerweise schneller. Auf der anderen Seite, wenn die Sättigung einige Komponenten entfernt, kann die direkte Berechnung dramatisch schneller sein.

Will man in Bezug auf mehrere Polynome oder in Bezug auf ein einzelnes Polynom, das ein Produkt ist , sättigen, gibt es drei Vorgehensweisen, die das gleiche Ergebnis liefern, aber sehr unterschiedliche Rechenzeiten haben können (je nachdem, welches Problem am effizientesten ist ). ${\displaystyle f_{1},\ldots,f_{k}}$${\displaystyle f=f_{1}\cdots f_{k},}$

• Sättigung durch in einer einzigen Gröbner-Basisrechnung.${\displaystyle f=f_{1}\cdots f_{k}}$
• Sättigung bis dann Sättigung des Ergebnisses um und so weiter.${\displaystyle f_{1},}$${\displaystyle f_{2},}$
• Addieren der Polynome zu F oder zu seiner Gröbner-Basis und Eliminieren der in einer einzigen Gröbner-Basis-Berechnung.${\displaystyle 1-t_{1}f_{1},\ldots ,1-t_{k}f_{k},}$${\displaystyle t_{i}}$

Effektiver Nullstellensatz

Hilberts Nullstellensatz hat zwei Versionen. Die erste behauptet, dass eine Menge von Polynomen eine leere Menge von gemeinsamen Nullstellen in einem algebraischen Abschluss des Koeffizientenkörpers genau dann hat, wenn 1 zum erzeugten Ideal gehört. Dies lässt sich leicht mit einer Gröbner-Basis-Berechnung überprüfen, da 1 genau dann zu einem Ideal gehört, wenn 1 zur Gröbner-Basis des Ideals gehört, für jede monomische Ordnung.

Die zweite Version behauptet, dass die Menge der gemeinsamen Nullstellen (in einem algebraischen Abschluss des Koeffizientenkörpers) eines Ideals genau dann in der Hyperfläche der Nullstellen eines Polynoms f enthalten ist , wenn eine Potenz von f zum Ideal gehört . Dies kann durch eine Sättigung des Ideals mit f getestet werden ; tatsächlich gehört eine Potenz von f genau dann zum Ideal, wenn die Sättigung durch f eine Gröbner-Basis mit 1 liefert.

Implizitisierung in einer höheren Dimension

Per Definition kann eine affine rationale Varietät der Dimension k durch parametrische Gleichungen der Form

${\displaystyle {\begin{aligned}x_{1}&={\frac {p_{1}}{p_{0}}}\\&\;\;\vdots \\x_{n}&={\ frac {p_{n}}{p_{0}}},\end{aligned}}}$

wo sind n +1 Polynome in den k Variablen (Parameter der Parametrisierung) Somit sind die Parameter und die Koordinaten der Punkte der Varietät Nullstellen des Ideals ${\displaystyle p_{0},\ldots ,p_{n}}$${\displaystyle t_{1},\ldots,t_{k}.}$${\displaystyle t_{1},\ldots,t_{k}}$${\displaystyle x_{1},\ldots,x_{n}}$

${\displaystyle I=\left\langle p_{0}x_{1}-p_{1},\ldots ,p_{0}x_{n}-p_{n}\right\rangle .}$

Man könnte vermuten, dass es ausreicht, die Parameter zu eliminieren, um die impliziten Gleichungen der Varietät zu erhalten, wie dies bei Kurven der Fall ist. Leider ist dies nicht immer der Fall. Wenn die einen gemeinsamen Nullpunkt haben (manchmal als Basispunkt bezeichnet ), ist jede irreduzible Komponente der nicht leeren algebraischen Menge, die durch definiert wird, eine irreduzible Komponente der durch I definierten algebraischen Menge . Daraus folgt, dass in diesem Fall die direkte Eliminierung von eine leere Menge von Polynomen liefert. ${\displaystyle p_{i}}$${\displaystyle p_{i}}$${\displaystyle t_{i}}$

Wenn k >1 ist, sind daher zwei Berechnungen auf der Gröbner-Basis erforderlich, um zu impliziten:

1. Sättigen Sie durch , um eine Gröbner-Basis zu erhalten${\displaystyle I}$${\displaystyle p_{0}}$${\displaystyle G}$
2. Eliminieren Sie das von , um eine Gröbner-Basis des Ideals (der impliziten Gleichungen) der Varietät zu erhalten.${\displaystyle t_{i}}$${\displaystyle G}$

Implementierungen

• CoCoA- freies Computeralgebrasystem zur Berechnung von Gröbner-Basen.
• GAP- freies Computeralgebrasystem, das Berechnungen mit Gröbner-Basen durchführen kann.
• FGb, Faugères eigene Implementierung seines F4-Algorithmus , verfügbar als Maple- Bibliothek. Bis heute, ab 2014, ist es mit Magma die schnellste Implementierung für rationale Koeffizienten und Koeffizienten in einem endlichen Körper Primzahlordnung.
• Macaulay 2 kostenlose Software zum Durchführen von Polynomberechnungen, insbesondere Gröbner-Basisberechnungen.
• Magma hat eine sehr schnelle Implementierung des F4-Algorithmus von Faugère.
• Maple verfügt über Implementierungen der Buchberger- und Faugère-F4-Algorithmen sowie des Gröbner-Trace.
• Mathematica beinhaltet eine Implementierung des Buchberger-Algorithmus mit leistungsverbessernden Techniken wie dem Gröbner Walk, Gröbner Trace und einer Verbesserung für torische Basen.
• EINZIGARTIGE freie Software zur Berechnung kommutativer und nichtkommutativer Gröbner-Basen.
• SageMath bietet eine einheitliche Schnittstelle zu mehreren Computeralgebrasystemen (einschließlich SINGULAR und Macaulay) und enthält einige eigene Gröbner-Basisalgorithmen.
• Das Computeralgebrasystem SymPy Python verwendet Gröbner-Basen, um polynomielle Systeme zu lösen.

Anwendungsbereiche

Fehlerkorrekturcodes

Die Gröbner-Basis wurde in der Theorie der fehlerkorrigierenden Codes für die algebraische Dekodierung angewendet. Unter Verwendung von Gröbner-Basisberechnungen an verschiedenen Formen fehlerkorrigierender Gleichungen wurden Decodierungsverfahren zur Korrektur von Fehlern von zyklischen Codes, affinen Varietätencodes, algebraisch-geometrischen Codes und sogar allgemeinen linearen Blockcodes entwickelt. Die Anwendung der Gröbner-Basis bei der algebraischen Dekodierung ist immer noch ein Forschungsgebiet der Kanalkodierungstheorie.

Siehe auch

Verweise

Weiterlesen

• Adams, William W.; Loustaunau, Philippe (1994). Eine Einführung in die Gröbner-Basen . Diplomstudium Mathematik . 3 . Amerikanische Mathematische Gesellschaft . ISBN 0-8218-3804-0.
• Li, Huishi (2011). Gröbner-Basen in der Ringtheorie . Weltwissenschaftlich . ISBN 978-981-4365-13-0.
• Becker, Thomas; Weispfenning, Volker (1998). Gröbner-Basen . Abschlusstexte der Mathematik. 141 . Springer. ISBN 0-387-97971-9.
• Buchberger, Bruno (1965). Ein Algorithmus zum Finden der Basiselemente des Restklassenrings eines nulldimensionalen Polynomideals (PDF) (PhD). Universität Innsbruck. — (2006). Übersetzt von Abramson, M. "Bruno Buchbergers Doktorarbeit 1965: Ein Algorithmus zum Finden der Basiselemente des Restklassenrings eines nulldimensionalen polynomialen Ideals" . Zeitschrift für symbolische Berechnung . 41 (3–4): 471–511. doi : 10.1016/j.jsc.2005.09.007 . [Dies ist die These von Buchberger über die Erfindung der Gröbner-Basen.]
• Buchberger, Bruno (1970). "Ein algorithmisches Kriterium für die Lösbarkeit eines Systems algebraischer Gleichungen" (PDF) . Aequationes Mathematicae . 4 : 374–383. doi : 10.1007/BF01844169 . S2CID  189834323 . (Dies ist die Zeitschriftenveröffentlichung von Buchbergers Dissertation.) Burchberger, B.; Winkler, F., Hrsg. (26. Februar 1998). „Ein algorithmisches Kriterium für die Lösbarkeit eines Systems algebraischer Gleichungen“ . Gröbner Grundlagen und Anwendungen . Vorlesungsreihe der London Mathematical Society. 251 . Cambridge University Press. S. 535–545. ISBN 978-0-521-63298-0.
• Buchberger, Bruno; Kauers, Manuel (2010). "Gröbner Basen" . Scholarpedia . 5 (10): 7763. doi : 10.4249/scholarpedia.7763 .
• Fröberg, Ralf (1997). Eine Einführung in die Gröbner-Basen . Wiley. ISBN 0-471-97442-0.
• Sturmfels, Bernd (November 2005). "Was ist ... eine Gröbner-Basis?" (PDF) . Mitteilungen der American Mathematical Society . 52 (10): 1199–1200, eine kurze EinführungCS1-Wartung: Postscript ( Link )
• Shirshov, Anatoliĭ I. (1999). "Bestimmte algorithmische Probleme für Lie-Algebren" (PDF) . ACM SIGSAM-Bulletin . 33 (2): 3–6. doi : 10.1145/334714.334715 . S2CID  37070503 .(übersetzt aus Sibirsk. Mat. Zh. Siberian Mathematics Journal 3 (1962), 292–296).
• Aschenbrenner, Matthias ; Hillar, Christoph (2007). "Endliche Generation symmetrischer Ideale" . Transaktionen der American Mathematical Society . 359 (11): 5171–92. doi : 10.1090/S0002-9947-07-04116-5 . S2CID  5656701 . (auf unendlichdimensionalen Gröbnerbasen für Polynomringe in unendlich vielen Unbestimmten).

Externe Links

• Faugères eigene Implementierung seines F4-Algorithmus
• "Gröbner Basis" , Enzyklopädie der Mathematik , EMS Press , 2001 [1994]
• Buchberger, B. (2003). "Gröbner-Grundlagen: Eine kurze Einführung für Systemtheoretiker" (PDF) . In Moreno-Diaz, R.; Buchberger, B.; Freire, J. (Hrsg.). Computer Aided Systems Theory — EUROCAST 2001: Eine Auswahl von Beiträgen des 8. Internationalen Workshops zur Computer Aided Systems Theory . Springer. S. 1–19. ISBN 978-3-540-45654-4.
• Buchberger, B.; Zapletal, A. "Gröbner Basen Bibliographie" .
• Vergleichende Timings-Seite für Gröbner Bases Software
• Prof. Bruno Buchberger Bruno Buchberger
• Weisstein, Eric W. "Gröbner Basis" . MathWorld .
• Einführung in die Gröbner-Basis auf Scholarpedia