Regression zum Mittelwert - Regression toward the mean

Galtons Versuchsaufbau (Abb.8)

In Statistiken , Regression zur Mitte (auch genannt Regression zur Mitte , Rückkehr zum Mittelwert , und die Reversion zur Mittelmäßigkeit ) ist das Phänomen , dass , wenn ein entsteht Abtastpunkt einer Zufallsvariable ist extremes (fast ein Ausreißer ), in welchem Fall eines Der zukünftige Punkt liegt wahrscheinlich näher am Mittelwert oder Durchschnitt . Um falsche Schlussfolgerungen zu vermeiden, muss bei der Gestaltung wissenschaftlicher Experimente und der Interpretation von Daten eine Regression zum Mittelwert berücksichtigt werden.

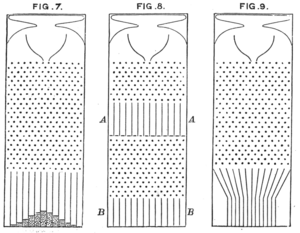
Die Bedingungen, unter denen eine Regression zum Mittelwert auftritt, hängen von der mathematischen Definition des Begriffs ab. Der britische Universalgelehrte Sir Francis Galton beobachtete das Phänomen erstmals im Zusammenhang mit der einfachen linearen Regression von Datenpunkten. Galton entwickelte das folgende Modell: Pellets fallen durch einen Quincunx , um eine normale Verteilung direkt unter ihrem Eintrittspunkt zu bilden. Diese Pellets könnten dann nach unten in eine zweite Galerie entsprechend einer zweiten Messung freigesetzt werden. Galton stellte dann die umgekehrte Frage: "Woher kamen diese Pellets?"

Die Antwort lautete nicht ' im Durchschnitt direkt darüber ' . Vielmehr war es ' im Durchschnitt mehr zur Mitte ' , aus dem einfachen Grund, dass darüber mehr Pellets zur Mitte hin nach links wandern konnten als im linken Extrem, die nach rechts, nach innen wandern konnten.

Als weniger restriktiver Ansatz kann die Regression zum Mittelwert für jede bivariate Verteilung mit identischen Randverteilungen definiert werden . Es gibt zwei solcher Definitionen. Eine Definition stimmt eng mit der üblichen Verwendung des Begriffs "Regression zum Mittelwert" überein. Nicht alle dieser bivariaten Verteilungen zeigen unter dieser Definition eine Regression zum Mittelwert. Alle diese bivariaten Verteilungen zeigen jedoch eine Regression zum Mittelwert unter der anderen Definition.

Jeremy Siegel verwendet den Begriff "Rückkehr zum Mittelwert", um eine Finanzzeitreihe zu beschreiben , in der "die Renditen kurzfristig sehr instabil, aber langfristig sehr stabil sein können". Quantitativ gesehen nimmt die Standardabweichung der durchschnittlichen Jahresrenditen schneller ab als der Kehrwert der Haltedauer , was bedeutet, dass der Prozess kein Random Walk ist , sondern dass Phasen mit niedrigeren Renditen systematisch von kompensierenden Phasen mit höheren Renditen gefolgt werden , wie es zum Beispiel in vielen Saisongeschäften der Fall ist.

Konzeptioneller Hintergrund

Betrachten Sie ein einfaches Beispiel: Eine Klasse von Schülern macht einen 100-Punkte-Richtig/Falsch-Test zu einem Thema. Angenommen, alle Schüler wählen zufällig bei allen Fragen. Dann wäre die Punktzahl jedes Schülers eine Realisierung eines Satzes unabhängiger und identisch verteilter Zufallsvariablen mit einem erwarteten Mittelwert von 50. Natürlich werden einige Schüler zufällig wesentlich über 50 und andere wesentlich unter 50 erzielen. Wenn man nur die 10 % der Schüler mit der höchsten Punktzahl auswählt und ihnen einen zweiten Test gibt, bei dem sie wieder zufällig alle Items auswählen, würde der Mittelwert wieder nahe bei 50 liegen. Der Mittelwert dieser Schüler würde sich also "regressieren". " bis zum Mittelwert aller Schüler, die den ursprünglichen Test abgelegt haben. Unabhängig davon, was ein Schüler im ursprünglichen Test erzielt, ist die beste Vorhersage seiner Punktzahl im zweiten Test 50.

Wenn die Auswahl der Antworten auf die Testfragen nicht zufällig war – dh wenn die Antworten der Schüler ohne Glück (gut oder schlecht) oder zufälliges Raten involviert waren –, dann würde erwartet, dass alle Schüler beim zweiten Test die gleichen Ergebnisse erzielen wie sie im ursprünglichen Test erzielt, und es würde keine Regression zum Mittelwert geben.

Die meisten realistischen Situationen liegen zwischen diesen beiden Extremen: Beispielsweise könnte man Prüfungsergebnisse als eine Kombination aus Geschick und Glück betrachten . In diesem Fall würde sich die Untergruppe der überdurchschnittlichen Schüler aus denjenigen zusammensetzen, die begabt waren und kein besonderes Pech hatten, zusammen mit denen, die ungelernt waren, aber sehr viel Glück hatten. Bei einem erneuten Test dieser Teilmenge ist es unwahrscheinlich, dass die ungelernten ihren Glücksfall wiederholen, während die erfahrenen eine zweite Chance haben, Pech zu haben. Daher ist es unwahrscheinlich, dass diejenigen, die zuvor gut abgeschnitten haben, im zweiten Test nicht ganz so gut abschneiden, selbst wenn das Original nicht reproduziert werden kann.

Das Folgende ist ein Beispiel für diese zweite Art der Regression zum Mittelwert. Eine Klasse von Studierenden legt an zwei aufeinanderfolgenden Tagen zwei Ausgaben desselben Tests ab. Es wurde häufig beobachtet, dass die schlechtesten Performer am ersten Tag ihre Ergebnisse am zweiten Tag tendenziell verbessern und die besten Performer am ersten Tag am zweiten Tag tendenziell schlechter abschneiden. Das Phänomen tritt auf, weil die Ergebnisse der Schüler teilweise durch die zugrunde liegenden Fähigkeiten und teilweise durch den Zufall bestimmt werden. Bei der ersten Prüfung haben einige Glück und punkten mehr als ihre Fähigkeiten, und einige haben Pech und punkten weniger als ihre Fähigkeiten. Einige der glücklichen Schüler beim ersten Test werden beim zweiten Test wieder Glück haben, aber mehr von ihnen haben (für sie) durchschnittliche oder unterdurchschnittliche Ergebnisse. Daher ist es wahrscheinlicher, dass ein Schüler, der beim ersten Test Glück hatte und seine Fähigkeiten übererfüllt hat, beim zweiten Test eine schlechtere als eine bessere Punktzahl hat. In ähnlicher Weise werden Schüler, die im ersten Test unglücklicherweise weniger als ihre Fähigkeiten erzielen, dazu neigen, ihre Ergebnisse im zweiten Test zu erhöhen. Je größer der Einfluss des Glücks bei der Erzeugung eines Extremereignisses ist, desto weniger wahrscheinlich wiederholt sich das Glück in mehreren Ereignissen.

Andere Beispiele

Wenn Ihre Lieblingssportmannschaft letztes Jahr die Meisterschaft gewonnen hat, was bedeutet das für ihre Gewinnchancen in der nächsten Saison? Soweit dieses Ergebnis auf Können zurückzuführen ist (die Mannschaft ist in guter Verfassung, mit einem Top-Trainer usw.), signalisiert ihr Sieg, dass es wahrscheinlicher ist, dass sie im nächsten Jahr wieder gewinnen wird. Doch je mehr Glück dies ist (andere Teams in einen Drogenskandal verwickelt, günstige Auslosung, Draft Picks erwiesen sich als produktiv usw.), desto unwahrscheinlicher ist es, dass sie im nächsten Jahr wieder gewinnen.

Wenn eine medizinische Studie darauf hindeutet, dass ein bestimmtes Medikament oder eine bestimmte Behandlung alle anderen Behandlungen für eine Erkrankung übertrifft, dann ist es in einer zweiten Studie wahrscheinlicher, dass das Medikament oder die Behandlung mit der besseren Leistung näher am Mittelwert liegt.

Wenn eine Geschäftsorganisation ein hochprofitables Quartal hat, obwohl die zugrunde liegenden Gründe für ihre Leistung unverändert sind, wird sie im nächsten Quartal wahrscheinlich weniger gut abschneiden.

Baseballspieler, die in ihrer Rookie-Saison gut getroffen haben, werden wahrscheinlich in ihrer zweiten Saison schlechter abschneiden; der " Sophomore Einbruch ". In ähnlicher Weise ist die Regression zum Mittelwert eine Erklärung für den Sports Illustrated- Cover-Jinx – Perioden außergewöhnlicher Leistungen, die zu einem Cover-Feature führen, werden wahrscheinlich von Perioden mittelmäßiger Leistung gefolgt, was den Eindruck erweckt, dass das Erscheinen auf dem Cover den Rückgang eines Athleten verursacht .

Geschichte

Der Begriff der Regression kommt aus der Genetik und wurde von popularisiert Sir Francis Galton während des späten 19. Jahrhunderts mit der Veröffentlichung der Regression in Richtung Mittelmäßigkeit in erblicher Statur . Galton beobachtete, dass extreme Eigenschaften (zB Größe) der Eltern nicht vollständig an ihre Nachkommen weitergegeben werden. Vielmehr sind die Eigenschaften bei den Nachkommen Regress zu einem mittelmäßigen Punkt (ein Punkt, der da als Mittelwert identifiziert wurde). Durch die Messung der Körpergröße von Hunderten von Menschen konnte er die Regression zum Mittelwert quantifizieren und die Größe des Effekts abschätzen. Galton schrieb, dass "die durchschnittliche Regression der Nachkommen ein konstanter Bruchteil ihrer jeweiligen mittleren elterlichen Abweichungen ist". Dies bedeutet, dass der Unterschied zwischen einem Kind und seinen Eltern für ein bestimmtes Merkmal proportional zur Abweichung seiner Eltern von typischen Personen in der Bevölkerung ist. Wenn ihre Eltern jeweils fünf Zentimeter größer sind als der Durchschnitt für Männer und Frauen, dann sind die Nachkommen im Durchschnitt um einen Faktor (der heute eins minus den Regressionskoeffizienten nennen würde ) mal fünf Zentimeter kleiner als ihre Eltern . Für die Körpergröße schätzte Galton diesen Koeffizienten auf etwa 2/3: Die Körpergröße eines Individuums misst ungefähr einen Mittelpunkt, der zwei Drittel der Abweichung der Eltern vom Bevölkerungsdurchschnitt beträgt.

Galton prägte den Begriff "Regression", um eine beobachtbare Tatsache bei der Vererbung multifaktorieller quantitativer genetischer Merkmale zu beschreiben: nämlich dass die Nachkommen von Eltern, die am Ende der Verteilung liegen, tendenziell näher am Zentrum, dem Mittelwert, liegen der Vertrieb. Er quantifizierte diesen Trend und erfand damit die lineare Regressionsanalyse und legte damit die Grundlage für einen Großteil der modernen statistischen Modellierung. Seitdem hat der Begriff "Regression" verschiedene Bedeutungen angenommen und kann von modernen Statistikern verwendet werden, um Phänomene des Sampling-Bias zu beschreiben , die wenig mit Galtons ursprünglichen Beobachtungen auf dem Gebiet der Genetik zu tun haben.

Obwohl seine mathematische Analyse richtig war, ist Galtons biologische Erklärung für das von ihm beobachtete Regressionsphänomen heute als falsch bekannt. Er sagte: "Ein Kind erbt teilweise von seinen Eltern, teilweise von seinen Vorfahren. Allgemein gesprochen, je weiter seine Genealogie zurückreicht, desto zahlreicher und vielfältiger werden seine Vorfahren, bis sie sich nicht mehr von jeder gleich zahlreichen zufälligen Stichprobe unterscheiden vom Rennen insgesamt." Dies ist falsch, da ein Kind sein Erbgut ausschließlich von seinen Eltern erhält. Es gibt kein Generations-Skipping im genetischen Material: Jegliches genetisches Material von früheren Vorfahren muss durch die Eltern hindurchgegangen sein (obwohl es möglicherweise nicht in ihnen exprimiert wurde). Das Phänomen wird besser verstanden, wenn wir davon ausgehen, dass das vererbte Merkmal (z. B. die Körpergröße) von einer großen Anzahl rezessiver Gene kontrolliert wird . Außergewöhnlich große Individuen müssen für Mutationen mit erhöhter Körpergröße an einem großen Teil dieser Loci homozygot sein . Aber die Loci, die diese Mutationen tragen, werden nicht notwendigerweise von zwei großen Individuen geteilt, und wenn sich diese Individuen paaren, werden ihre Nachkommen im Durchschnitt für "große" Mutationen auf weniger Loci homozygot sein als ihre Eltern. Darüber hinaus ist die Körpergröße nicht ausschließlich genetisch bedingt, sondern unterliegt während der Entwicklung auch Umwelteinflüssen, die die Nachkommen außergewöhnlicher Eltern noch eher durchschnittlich als ihre Eltern verhalten.

Dieses populationsgenetische Phänomen der Regression zum Mittelwert kann man sich am besten als Kombination eines binomial verteilten Vererbungsprozesses mit normalverteilten Umwelteinflüssen vorstellen. Im Gegensatz dazu wird der Begriff "Regression zum Mittelwert" heute häufig verwendet, um das Phänomen zu beschreiben, durch das eine anfängliche Stichprobenverzerrung verschwinden kann, wenn neue, wiederholte oder größere Stichproben Stichprobenmittelwerte anzeigen, die näher am tatsächlichen zugrunde liegenden Grundgesamtheitsmittelwert liegen.

Bedeutung

Die Regression zum Mittelwert ist eine wichtige Überlegung bei der Versuchsplanung .

Nehmen Sie ein hypothetisches Beispiel von 1.000 Personen ähnlichen Alters, die untersucht und hinsichtlich des Risikos, einen Herzinfarkt zu erleiden, bewertet wurden. Statistiken könnten verwendet werden, um den Erfolg einer Intervention an den 50 Personen zu messen, die mit dem höchsten Risiko bewertet wurden. Die Intervention kann eine Ernährungsumstellung, Bewegung oder eine medikamentöse Behandlung sein. Auch wenn die Interventionen wertlos sind, wird erwartet, dass die Testgruppe bei der nächsten körperlichen Untersuchung aufgrund der Regression zum Mittelwert eine Verbesserung zeigt. Der beste Weg, diesen Effekt zu bekämpfen, besteht darin, die Gruppe nach dem Zufallsprinzip in eine Behandlungsgruppe, die die Behandlung erhält, und eine Kontrollgruppe , die dies nicht tut , aufzuteilen . Die Behandlung würde dann nur dann als wirksam beurteilt, wenn sich die Behandlungsgruppe stärker verbessert als die Kontrollgruppe.

Alternativ könnte eine Gruppe benachteiligter Kinder getestet werden, um diejenigen mit dem höchsten Hochschulpotenzial zu ermitteln. Die besten 1% konnten identifiziert und mit speziellen Anreicherungskursen, Nachhilfe, Beratung und Computern versorgt werden. Selbst wenn das Programm effektiv ist, können ihre durchschnittlichen Ergebnisse bei einer Wiederholung des Tests ein Jahr später niedriger ausfallen. Unter diesen Umständen kann es jedoch als unethisch angesehen werden, eine Kontrollgruppe benachteiligter Kinder zu haben, deren besondere Bedürfnisse ignoriert werden. Eine mathematische Schrumpfungsberechnung kann diesen Effekt ausgleichen, ist aber nicht so zuverlässig wie die Kontrollgruppenmethode (siehe auch Steins Beispiel ).

Der Effekt kann auch für allgemeine Inferenz und Schätzung ausgenutzt werden. Am heißesten Ort des Landes ist es heute wahrscheinlicher, dass es morgen kühler als heißer ist als heute. Der Investmentfonds mit der besten Performance der letzten drei Jahre wird in den nächsten drei Jahren eher einen Rückgang der relativen Performance verzeichnen als sich verbessern. Der erfolgreichste Hollywood-Schauspieler dieses Jahres wird wahrscheinlich weniger Brutto als mehr für seinen nächsten Film haben. Der Baseballspieler mit dem höchsten Schlagdurchschnitt nach dem All-Star-Break hat in der zweiten Saisonhälfte eher einen niedrigeren als einen höheren Durchschnitt.

Missverständnisse

Das Konzept der Regression zum Mittelwert kann sehr leicht missbraucht werden.

Im obigen Schülertestbeispiel wurde implizit angenommen, dass sich das Gemessene zwischen den beiden Messungen nicht ändert. Nehmen wir jedoch an, der Kurs sei bestanden/nicht bestanden und die Schüler müssten in beiden Tests mehr als 70 Punkte erzielen, um zu bestehen. Dann hätten die Schüler, die beim ersten Mal weniger als 70 Punkte erzielten, keinen Anreiz, gut abzuschneiden, und könnten beim zweiten Mal im Durchschnitt schlechter abschneiden. Die knapp über 70-Jährigen hingegen hätten einen starken Anreiz, während der Prüfung zu lernen und sich zu konzentrieren. In diesem Fall könnte man eine Bewegung von 70 weg sehen , Werte darunter werden niedriger und Werte darüber werden höher. Es ist möglich, dass Änderungen zwischen den Messzeitpunkten die statistische Regressionstendenz zum Mittelwert erhöhen, aufheben oder umkehren.

Die statistische Regression zum Mittelwert ist kein kausales Phänomen. Ein Schüler mit der schlechtesten Punktzahl im Test am ersten Tag wird seine Punktzahl am zweiten Tag aufgrund des Effekts nicht unbedingt wesentlich erhöhen. Im Durchschnitt verbessern sich die schlechtesten Scorer, aber das ist nur so, weil die schlechtesten Scorer eher Pech als Glück hatten. In dem Maße, in dem eine Punktzahl zufällig bestimmt wird oder dass eine Punktzahl zufällige Schwankungen oder Fehler aufweist, im Gegensatz dazu, dass sie durch die akademischen Fähigkeiten des Schülers bestimmt wird oder ein "wahrer Wert" ist, hat das Phänomen eine Wirkung. Ein klassischer Fehler in dieser Hinsicht war in der Bildung. Die Schüler, die für gute Arbeit gelobt wurden, schnitten bei der nächsten Maßnahme schlechter ab, und die Schüler, die für schlechte Arbeit bestraft wurden, schnitten bei der nächsten Maßnahme besser ab. Die Pädagogen beschlossen, auf dieser Grundlage nicht mehr zu loben und weiter zu bestrafen. Eine solche Entscheidung war ein Fehler, denn die Regression zum Mittelwert beruht nicht auf Ursache und Wirkung, sondern eher auf zufälligen Fehlern in einer natürlichen Verteilung um einen Mittelwert.

Obwohl extreme Einzelmessungen zum Mittelwert zurückfallen, wird die zweite Stichprobe der Messwerte nicht näher am Mittelwert liegen als die erste. Betrachten Sie die Schüler noch einmal. Nehmen wir an, die Tendenz extremer Personen besteht darin, 10 % des Weges in Richtung des Mittelwerts von 80 zurückzufallen, also wird erwartet , dass ein Schüler, der am ersten Tag 100 Punkte erzielt hat, am zweiten Tag 98 Punkte erzielt, und ein Student, der am ersten Tag 70 Punkte erzielt hat Score 71 am zweiten Tag. Diese Erwartungen liegen näher am Mittelwert als die Ergebnisse des ersten Tages. Aber die Punktzahlen des zweiten Tages werden je nach Erwartungen variieren; einige werden höher und einige niedriger sein. Darüber hinaus sollten Personen, die sehr nahe am Mittelwert messen, damit rechnen, sich vom Mittelwert zu entfernen. Der Effekt ist die genaue Umkehrung der Regression zum Mittelwert und gleicht diesen genau aus. Für extreme Individuen erwarten wir also, dass der zweite Wert näher am Mittelwert liegt als der erste Wert, aber für alle Individuen erwarten wir, dass die Verteilung der Entfernungen vom Mittelwert in beiden Messreihen gleich ist.

Bezogen auf den obigen Punkt funktioniert die Regression zum Mittelwert in beide Richtungen gleich gut. Wir erwarten, dass der Schüler mit der höchsten Testnote am zweiten Tag am ersten Tag schlechter abgeschnitten hat. Und wenn wir den besten Schüler am ersten Tag mit dem besten Schüler am zweiten Tag vergleichen, unabhängig davon, ob es sich um dieselbe Person handelt oder nicht, besteht die Tendenz, in beide Richtungen zum Mittelwert zurückzufallen. Wir erwarten, dass die besten Ergebnisse an beiden Tagen gleich weit vom Mittelwert entfernt sind.

Regressionsirrtümer

Viele Phänomene werden tendenziell auf die falschen Ursachen zurückgeführt, wenn die Regression auf den Mittelwert nicht berücksichtigt wird.

Ein extremes Beispiel ist Horace Secrists Buch The Triumph of Medocrity in Business aus dem Jahr 1933 , in dem der Statistikprofessor Berge von Daten sammelte, um zu beweisen, dass die Profitraten wettbewerbsfähiger Unternehmen im Laufe der Zeit zum Durchschnitt tendieren. Tatsächlich gibt es keinen solchen Effekt; die Variabilität der Gewinnraten ist im Zeitverlauf nahezu konstant. Secrist hatte nur die übliche Regression zum Mittelwert beschrieben. Ein verärgerter Rezensent, Harold Hotelling , verglich das Buch damit, „das Einmaleins zu beweisen, indem man Elefanten in Reihen und Spalten anordnet und dann dasselbe für zahlreiche andere Tierarten macht“.

Die Berechnung und Interpretation von „Verbesserungswerten“ bei standardisierten Bildungstests in Massachusetts liefert wahrscheinlich ein weiteres Beispiel für den Regressionsfehler. 1999 erhielten die Schulen Verbesserungsziele. Für jede Schule hat das Bildungsministerium den Unterschied in der durchschnittlichen Punktzahl der Schüler in den Jahren 1999 und 2000 tabelliert. Es wurde schnell festgestellt, dass die meisten Schulen mit den schlechtesten Leistungen ihre Ziele erreicht hatten, was das Bildungsministerium als Bestätigung betrachtete die Solidität ihrer Politik. Es wurde jedoch auch festgestellt, dass viele der angeblich besten Schulen im Commonwealth, wie die Brookline High School (mit 18 Finalisten des National Merit Scholarship) für gescheitert erklärt wurden. Wie in vielen Fällen, die Statistik und öffentliche Ordnung betreffen, wird das Thema diskutiert, aber in den Folgejahren wurden keine "Verbesserungsergebnisse" bekannt gegeben, und die Ergebnisse scheinen eine Regression zum Mittelwert zu sein.

Der Psychologe Daniel Kahneman , Gewinner des Nobel-Gedächtnispreises für Wirtschaftswissenschaften 2002 , wies darauf hin, dass eine Regression zum Mittelwert erklären könnte, warum Zurechtweisungen die Leistung zu verbessern scheinen, während Lob nach hinten losgeht.

Ich hatte die befriedigendste Eureka-Erfahrung meiner Karriere, als ich versuchte, Fluglehrern beizubringen, dass Lob für die Förderung des Erlernens von Fertigkeiten effektiver ist als Bestrafung. Als ich meine begeisterte Rede beendet hatte, hob einer der erfahrensten Ausbilder aus dem Publikum die Hand und hielt seine eigene kurze Rede, die damit begann, dass positive Verstärkung gut für die Vögel sein könnte, aber dann leugnete, dass sie optimal war für Flugschüler. Er sagte: „Bei vielen Gelegenheiten habe ich Flugkadetten für die saubere Ausführung einiger Kunstflugmanöver gelobt, und im Allgemeinen schneiden sie es noch einmal schlechter ab, wenn sie es erneut versuchen Im Allgemeinen machen sie es beim nächsten Mal besser. Sagen Sie uns also bitte nicht, dass Verstärkung funktioniert und Bestrafung nicht, denn das Gegenteil ist der Fall." Dies war ein freudiger Moment, in dem ich eine wichtige Wahrheit über die Welt verstand: Weil wir dazu neigen, andere zu belohnen, wenn sie es gut machen, und sie zu bestrafen, wenn sie es schlecht machen, und weil es eine Regression zum Mittelwert gibt, ist es ein Teil des Menschlichen Bedingung, dass wir statistisch dafür bestraft werden, dass wir andere belohnen, und dass wir dafür belohnt werden, dass wir sie bestrafen. Ich arrangierte sofort eine Demonstration, bei der jeder Teilnehmer hinter seinem Rücken zwei Münzen auf eine Zielscheibe warf, ohne jegliche Rückmeldung. Wir haben die Entfernungen zum Ziel gemessen und konnten feststellen, dass diejenigen, die beim ersten Mal am besten abgeschnitten hatten, sich beim zweiten Versuch größtenteils verschlechtert hatten und umgekehrt. Aber ich wusste, dass diese Demonstration die Auswirkungen einer lebenslangen Exposition gegenüber einer perversen Kontingenz nicht rückgängig machen würde.

Um Kahnemans Geschichte einfach auszudrücken: Wenn man einen schweren Fehler macht, wird die Leistung später in der Regel sowieso auf ihr durchschnittliches Niveau zurückkehren. Dies wird als eine Verbesserung und als "Beweis" für die Überzeugung erscheinen, dass es besser ist, zu kritisieren als zu loben (besonders von jedem, der in diesem "niedrigen" Moment bereit ist, zu kritisieren). Im Gegenteil, wenn jemand überdurchschnittliche Leistungen erbringt, wird seine Leistung später auch tendenziell wieder auf sein durchschnittliches Niveau zurückkehren; die Änderung wird als Verschlechterung wahrgenommen und ein erstes Lob nach der ersten Aufführung als Ursache dieser Verschlechterung. Gerade weil das Kritisieren oder Loben der Regression zum Mittel vorausgeht, wird dem Kritisieren oder Loben fälschlicherweise Kausalität zugeschrieben. Die Regressionsfalle auch in erklärt Rolf Dobelli ist die Art klar zu denken .

Die britischen Strafverfolgungsbehörden haben die sichtbare Aufstellung von statischen oder mobilen Radarkameras an Unfallschwerpunkten gefördert . Begründet wurde diese Politik mit der Wahrnehmung, dass es nach dem Aufstellen einer Kamera zu einer entsprechenden Reduzierung schwerer Straßenverkehrsunfälle kommt. Statistiker haben jedoch darauf hingewiesen, dass, obwohl es einen Nettonutzen für gerettete Leben gibt, die Nichtberücksichtigung der Auswirkungen der Regression auf den Mittelwert dazu führt, dass die positiven Auswirkungen überbewertet werden.

Statistische Analysten haben seit langem den Effekt der Regression auf den Mittelwert im Sport erkannt; sie haben dafür sogar einen besonderen Namen: den „ Sophomore Slump “. Zum Beispiel, Carmelo Anthony von der NBA ‚s Denver Nuggets hatte eine hervorragende Rookie - Saison im Jahr 2004. Es war so hervorragend , dass er es nicht erwarten konnte , wiederholen: Im Jahr 2005 hatte Anthony Zahlen aus seiner Rookie - Saison gesunken. Die Gründe für den "Einbruch im zweiten Jahr" sind im Überfluss vorhanden, da Sport auf Anpassung und Gegenanpassung angewiesen ist, aber auf Glück basierende Spitzenleistungen als Rookie sind ein ebenso guter Grund wie jeder andere. Eine Regression auf den Mittelwert der sportlichen Leistung kann auch den scheinbaren „ Sports Illustrated-Cover-Jinx “ und den „ Wahnsinnigen Fluch “ erklären . John Hollinger hat einen alternativen Namen für das Phänomen der Regression zum Mittelwert: die "Zufallsregel", während Bill James es das "Plexiglas-Prinzip" nennt.

Da sich die populäre Überlieferung auf die Regression zum Mittelwert als Erklärung für die abnehmende Leistung von Athleten von einer Saison zur nächsten konzentriert hat, hat sie normalerweise die Tatsache übersehen, dass eine solche Regression auch für eine verbesserte Leistung verantwortlich sein kann. Betrachtet man beispielsweise den Schlagdurchschnitt der Major League Baseball- Spieler in einer Saison, tendieren diejenigen, deren Schlagdurchschnitt über dem Ligamittelwert lag, dazu, im folgenden Jahr nach unten in Richtung des Mittelwerts zurückzufallen, während diejenigen, deren Schlagdurchschnitt unter dem Mittelwert lag, tendenziell nach oben zum Mittelwert des folgenden Jahres.

Andere statistische Phänomene

Die Regression zum Mittelwert besagt einfach, dass das nächste zufällige Ereignis nach einem extremen Zufallsereignis wahrscheinlich weniger extrem ist. In keiner Weise "kompensiert" oder "ausgleicht" das zukünftige Ereignis das vorherige Ereignis, obwohl dies im Irrtum des Spielers (und dem abweichenden Gesetz der Durchschnitte ) angenommen wird. Auch das Gesetz der großen Zahl besagt, dass der Durchschnitt langfristig in Richtung des Erwartungswertes tendieren wird, macht aber keine Aussage über einzelne Versuche. Nach einer Serie von 10 Köpfen bei einem fairen Münzwurf (ein seltenes, extremes Ereignis) besagt die Regression zum Mittelwert, dass die nächste Serie von Kopf wahrscheinlich weniger als 10 sein wird, während das Gesetz der großen Zahlen besagt, dass Langfristig wird sich dieses Ereignis wahrscheinlich durchschnittlich auszahlen, und der durchschnittliche Anteil der Köpfe wird auf 1/2 tendieren. Im Gegensatz dazu geht der Irrtum des Spielers fälschlicherweise davon aus, dass die Münze jetzt "fällig" ist, damit eine Folge von Zahlen ausgeglichen wird.

Der gegenteilige Effekt ist die Regression zum Schwanz, die sich aus einer Verteilung mit nicht verschwindender Wahrscheinlichkeitsdichte gegen unendlich ergibt

Definition für einfache lineare Regression von Datenpunkten

Dies ist die Definition der Regression zum Mittelwert, die der ursprünglichen Verwendung von Sir Francis Galton eng folgt .

Angenommen, es gibt n Datenpunkte { y _i , x _i }, wobei i  = 1, 2, ..., n ist . Wir wollen die Gleichung der Regressionsgeraden finden , also der Geraden

${\displaystyle y=\alpha +\betax,\,}$

was eine "beste" Anpassung für die Datenpunkte bieten würde. (Beachten Sie, dass eine gerade Linie möglicherweise nicht die geeignete Regressionskurve für die gegebenen Datenpunkte ist.) Hier wird das "Beste" wie im Ansatz der kleinsten Quadrate verstanden : eine solche Linie, die die Summe der quadrierten Residuen der linearen Regression minimiert Modell. Mit anderen Worten lösen die Zahlen α und β das folgende Minimierungsproblem:

Finden , wo${\displaystyle \min_{\alpha,\,\beta}Q(\alpha,\beta)}$${\displaystyle Q(\alpha,\beta)=\sum_{i=1}^{n}{\hat {\varepsilon}}_{i}^{\,2}=\sum_{i=1 }^{n}(y_{i}-\alpha -\beta x_{i})^{2}\ }$

Verwendung von Zahnstein nachgewiesen werden kann , dass die Werte von α und β , daß die Zielfunktion minimieren Q sind

${\displaystyle {\begin{ausgerichtet}&{\hat {\beta}}={\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})( y_{i}-{\bar{y}})}{\sum_{i=1}^{n}(x_{i}-{\bar{x}})^{2}}}={\ frac {{\overline {xy}}-{\bar {x}}{\bar {y}}}{{\overline {x^{2}}}-{\bar {x}}^{2}} }={\frac {\operatorname {Cov} [x,y]}{\operatorname {Var} [x]}}=r_{xy}{\frac {s_{y}}{s_{x}}}, \\&{\hat{\alpha}}={\bar{y}}-{\hat{\beta}}\,{\bar{x}},\end{ausgerichtet}}}$

wobei r _xy der Stichprobenkorrelationskoeffizient zwischen x und y ist , s _x die Standardabweichung von x ist und s _y entsprechend die Standardabweichung von y ist . Ein horizontaler Balken über einer Variablen bedeutet den Stichprobendurchschnitt dieser Variablen. Zum Beispiel:${\displaystyle {\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .}$

Einsetzen der obigen Ausdrücke für und in die angepassten Werte ${\displaystyle {\hat {\alpha}}}$${\displaystyle {\hat {\beta}}}$${\displaystyle y=\alpha +\betax,\,}$

${\displaystyle {\hat{y}}={\hat{\alpha}}+{\hat{\beta}}x,\,}$

was ergibt

${\displaystyle {\frac {{\hat {y}}-{\bar {y}}}{s_{y}}}=r_{xy}{\frac {x-{\bar {x}}}{ s_{x}}}}$

Dies zeigt die Rolle, die r _xy in der Regressionsgerade standardisierter Datenpunkte spielt.

Wenn −1 <  r _xy  < 1, dann sagen wir, dass die Datenpunkte eine Regression zum Mittelwert aufweisen. Mit anderen Worten, wenn die lineare Regression das geeignete Modell für einen Satz von Datenpunkten ist, deren Stichprobenkorrelationskoeffizient nicht perfekt ist, dann gibt es eine Regression zum Mittelwert. Der vorhergesagte (oder angepasste) standardisierte Wert von y liegt näher an seinem Mittelwert als der standardisierte Wert von x an seinem Mittelwert.

Definitionen für bivariate Verteilung mit identischen Randverteilungen

Restriktive Definition

Lassen X ₁ , X ₂ be Zufallsvariablen mit identischen Randverteilungen mit Mittelwert μ . In dieser Formalisierung sagt man , dass die bivariate Verteilung von X ₁ und X ₂ eine Regression zum Mittelwert aufweist, wenn für jede Zahl c  >  μ gilt:

μ  ≤ E[ X ₂  | X ₁  =  c ] <  c ,

wobei die umgekehrten Ungleichungen für c  <  μ gelten .

Das Folgende ist eine informelle Beschreibung der obigen Definition. Betrachten Sie eine Population von Widgets . Jedes Widget hat zwei Zahlen, X ₁ und X ₂ (sagen wir, seine linke Spanne ( X ₁ ) und ihre rechte Spanne ( X ₂ )). Angenommen, die Wahrscheinlichkeitsverteilungen von X ₁ und X ₂ in der Grundgesamtheit sind identisch und die Mittelwerte von X ₁ und X ₂ sind beide μ . Wir nehmen nun ein zufälliges Widget aus der Population und bezeichnen seinen X ₁ -Wert mit c . (Beachten Sie, dass c größer, gleich oder kleiner als μ sein kann .) Wir haben noch keinen Zugriff auf den Wert von X ₂ dieses Widgets . Lassen Sie d den erwarteten Wert von X ₂ dieses speziellen Widgets bezeichnen. ( Dh Let d den Durchschnittswert der Bezeichnung X ₂ aller Widgets in der Population mit X ₁ = c .) , Wenn folgende Bedingung erfüllt ist:

Was auch immer der Wert c ist, d liegt zwischen μ und c ( dh d ist näher an μ als c ),

dann sagen wir, dass X ₁ und X ₂ eine Regression zum Mittelwert zeigen .

Diese Definition stimmt eng mit der gegenwärtigen allgemeinen Verwendung überein, die sich aus Galtons ursprünglicher Verwendung des Begriffs "Regression zum Mittelwert" entwickelt hat. Es ist "restriktiv" in dem Sinne, dass nicht jede bivariate Verteilung mit identischen Randverteilungen eine Regression zum Mittelwert (unter dieser Definition) aufweist.

Satz

Wenn ein Paar ( X ,  Y ) von einer Zufallsvariablen folgt bivariate Normalverteilung , so wird der bedingte Mittelwert E ( Y | X ) ist eine lineare Funktion von X . Der Korrelationskoeffizient r zwischen X und Y bestimmt zusammen mit den Randmittelwerten und Varianzen von X und Y diese lineare Beziehung:

${\displaystyle {\frac {E(Y\mid X)-E[Y]}{\sigma_{y}}}=r{\frac {XE[X]}{\sigma_{x}}}, }$

wobei E[X] und E[Y] die erwarteten Werte von X bzw. Y sind und _x und σ _y die Standardabweichungen von X bzw. Y sind.

Daraus ergibt sich die bedingte Erwartungswert von Y , da X ist t Standardabweichungen über seinem Mittelwert (und das schließt den Fall ein, wo er unter seinem Mittelwert ist, wenn t  <0), wird rt Standardabweichungen über dem Mittelwert von Y . Seit | r | ≤ 1, Y ist nicht weiter vom Mittelwert entfernt als X , gemessen in der Anzahl der Standardabweichungen.

Wenn also 0  r  < 1, dann zeigt ( X ,  Y ) eine Regression zum Mittelwert (nach dieser Definition).

Allgemeine Definition

Die folgende Definition der Reversion zum Mittelwert wurde von Samuels als Alternative zu der restriktiveren Definition der Regression zum Mittelwert oben vorgeschlagen.

Lassen X ₁ , X ₂ be Zufallsvariablen mit identischen Randverteilungen mit Mittelwert μ . In dieser Formalisierung sagt man , dass die bivariate Verteilung von X ₁ und X ₂ eine Reversion zum Mittelwert aufweist, wenn für jede Zahl c gilt

μ  ≤ E[ X ₂  | X ₁  >  c ] < E[ X ₁  | X ₁  >  c ], und

μ  ≥ E[ X ₂  | X ₁  <  c ] > E[ X ₁  | X ₁  <  c ]

Diese Definition ist "allgemein" in dem Sinne, dass jede bivariate Verteilung mit identischen Randverteilungen eine Rückkehr zum Mittelwert aufweist .

Siehe auch

• Hardy-Weinberg-Prinzip
• Interne Gültigkeit
• Gesetz der großen Zahlen
• Martingal
• Regressionsverdünnung
• Selektionsbias

Verweise

Weiterlesen

• JM Bland und GD Altman (Juni 1994). "Statistische Anmerkungen: Regression zum Mittelwert" . Britisches medizinisches Journal . 308 (6942): 1499. doi : 10.1136/bmj.308.6942.1499 . PMC  2540330 . PMID  8019287 . Artikel, einschließlich eines Diagramms von Galtons Originaldaten.

• Michael R. Chernick & Robert H. Friis (2003). Einführende Biostatistik für die Gesundheitswissenschaften . Wiley-Interscience . P. 272. ISBN 978-0-471-41137-6.

• Edward J. Dudewicz & Satya N. Mishra (1988). "Abschnitt 14.1: Schätzung von Regressionsparametern; Lineare Modelle". Moderne mathematische Statistik . John Wiley & Söhne . ISBN 978-0-471-81472-6.

• Francis Galton (1886). "Regression zur Mittelmäßigkeit bei erblicher Statur" (PDF) . Das Journal des Anthropologischen Instituts von Großbritannien und Irland . 15 : 246–263. doi : 10.2307/2841583 . JSTOR  2841583 .

• Donald F. Morrison (1967). „Kapitel 3: Stichproben aus der multivariaten Normalbevölkerung“. Multivariate statistische Methoden . McGraw-Hill . ISBN 978-0-534-38778-5.

• Stephen M. Stigler (1999). "Kapitel 9". Statistik auf dem Tisch . Harvard University Press .

• Myra L. Samuels (November 1991). „Statistische Reversion zum Mittelwert: universeller als Regression zum Mittelwert“. Der amerikanische Statistiker . 45 (4): 344–346. doi : 10.2307/2684474 . JSTOR  2684474 .
• Stephen Senn. Regression: Ein neuer Modus für eine alte Bedeutung , The American Statistician , Bd. 44, Nr. 2 (Mai 1990), S. 181–183.
• David C. Schmittlein. Überraschende Schlussfolgerungen aus nicht überraschenden Beobachtungen: Regressieren bedingte Erwartungen wirklich zum Mittelwert? The American Statistician , Band 43, Nr. 3 (August 1989), S. 176–183.
• Regression zum Mittelwert und das Studium der Veränderung , Psychological Bulletin
• Eine nicht mathematische Erklärung der Regression zum Mittelwert.
• Eine Simulation der Regression zum Mittelwert.
• Amanda Wachsmuth, Leland Wilkinson, Gerard E. Dallal. Galtons Biegung: Eine unentdeckte Nichtlinearität in Galtons Regressionsdaten zur Familienstatur und eine wahrscheinliche Erklärung basierend auf den Staturdaten von Pearson und Lee (Ein moderner Blick auf Galtons Analyse.)
• Massachusetts standardisierte Testergebnisse, interpretiert von einem Statistiker als Beispiel für Regression: siehe Diskussion in sci.stat.edu und seine Fortsetzung .
• Gary Smith , What the Luck: The Surprising Role of Chance in Our Everyday Lives, New York: Overlook, London: Duckworth. ISBN  978-1-4683-1375-8 .

Externe Links

• Medien im Zusammenhang mit der Regression zum Mittelwert bei Wikimedia Commons