Gewöhnliche kleinste Quadrate - Ordinary least squares

In der Statistik ist Ordinary Least Squares ( OLS ) eine Art der Methode der linearen kleinsten Quadrate zum Schätzen der unbekannten Parameter in einem linearen Regressionsmodell . OLS wählt die Parameter einer linearen Funktion eines Satzes erklärender Variablen nach dem Prinzip der kleinsten Quadrate : Minimierung der Summe der Quadrate der Differenzen zwischen der beobachteten abhängigen Variablen (Werte der beobachteten Variablen) im gegebenen Datensatz und den vorhergesagten durch die lineare Funktion der unabhängigen Variablen .

Geometrisch gesehen ist dies die Summe der quadrierten Distanzen parallel zur Achse der abhängigen Variablen zwischen jedem Datenpunkt in der Menge und dem entsprechenden Punkt auf der Regressionsfläche – je kleiner die Differenzen, desto besser passt das Modell an die Daten . Der resultierende Schätzer kann durch eine einfache Formel ausgedrückt werden, insbesondere im Fall einer einfachen linearen Regression , bei der auf der rechten Seite der Regressionsgleichung ein einzelner Regressor steht .

Die OLS Schätzer ist konsistent , wenn die Regressoren sind exogene und-durch die Gauss-Markov - Theorem - optimal in der Klasse der linear unbiased Schätzern , wenn die Fehler sind homoskedastisch und seriell unkorreliert . Unter diesen Bedingungen bietet das OLS-Verfahren eine mittelwertverzerrte Schätzung mit minimaler Varianz, wenn die Fehler endliche Varianzen aufweisen . Unter der zusätzlichen Annahme, dass die Fehler normalverteilt sind , ist OLS der Maximum-Likelihood-Schätzer .

Lineares Modell

Okun Gesetz in Makroökonomie heißt es, dass in einer Volkswirtschaft des BIP - Wachstum auf den Veränderungen der Arbeitslosenquote linear abhängen. Hier wird die gewöhnliche Methode der kleinsten Quadrate verwendet, um die Regressionsgerade zu konstruieren, die dieses Gesetz beschreibt.

Angenommen, die Daten bestehen aus Beobachtungen . Jede Beobachtung enthält eine Skalarantwort und einen Spaltenvektor von Parametern (Regressoren), dh . In einem linearen Regressionsmodell ist die Antwortvariable , eine lineare Funktion der Regressoren: ${\displaystyle n}$ ${\displaystyle \left\{\mathbf{x}_{i},y_{i}\right\}_{i=1}^{n}}$${\displaystyle i}$${\displaystyle y_{i}}$${\displaystyle \mathbf {x} _{i}}$${\displaystyle p}$${\displaystyle \mathbf {x} _{i}=\left[x_{i1},x_{i2},\dots,x_{ip}\right]^{\mathsf {T}}}$${\displaystyle y_{i}}$

${\displaystyle y_{i}=\beta_{1}\x_{i1}+\beta_{2}\x_{i2}+\cdots+\beta_{p}\x_{ip}+\varepsilon_ {ich},}$

oder in Vektorform ,

${\displaystyle y_{i}=\mathbf{x}_{i}^{\mathsf{T}}{\boldsymbol {\beta}}+\varepsilon_{i},\,}$

wobei , wie zuvor eingeführt, ein Spaltenvektor der -ten Beobachtung aller erklärenden Variablen ist; ein Vektor unbekannter Parameter ist; und der Skalar repräsentiert unbeobachtete Zufallsvariablen ( Fehler ) der -ten Beobachtung. berücksichtigt die Einflüsse auf die Antworten aus anderen Quellen als den Erklärern . Dieses Modell kann auch in Matrixnotation geschrieben werden als ${\displaystyle \mathbf {x} _{i}}$${\displaystyle i}$${\displaystyle {\boldsymbol {\beta}}}$${\displaystyle p\times 1}$${\displaystyle \varepsilon_{i}}$${\displaystyle i}$${\displaystyle \varepsilon_{i}}$${\displaystyle y_{i}}$${\displaystyle \mathbf {x} _{i}}$

${\displaystyle \mathbf{y} =\mathrm {X} {\boldsymbol {\beta}}+{\boldsymbol {\varepsilon}},\,}$

wo und sind Vektoren der Reaktionsvariablen und die Fehler der Beobachtungen und eine Matrix von Regressoren, manchmal auch die angerufene Design - Matrix , deren Zeile ist , und enthält die -te Beobachtungen auf allen erklärenden Variablen. ${\displaystyle \mathbf{y}}$${\displaystyle {\boldsymbol {\varepsilon}}}$${\displaystyle n\mal 1}$${\displaystyle n}$${\displaystyle\mathrm{X}}$${\displaystyle n\mal p}$${\displaystyle i}$${\displaystyle \mathbf{x}_{i}^{\mathsf{T}}}$${\displaystyle i}$

In der Regel wird der konstante Term immer in die Menge der Regressoren aufgenommen , etwa indem man für alle nimmt . Der diesem Regressor entsprechende Koeffizient wird als Achsenabschnitt bezeichnet . ${\displaystyle\mathrm{X}}$${\displaystyle x_{i1}=1}$${\displaystyle i=1,\dots,n}$${\displaystyle \beta_{1}}$

Regressoren müssen nicht unabhängig sein: Zwischen den Regressoren kann jede beliebige Beziehung bestehen (sofern es sich nicht um eine lineare Beziehung handelt). Wir könnten zum Beispiel vermuten, dass die Antwort sowohl von einem Wert als auch von seinem Quadrat linear abhängt; in diesem Fall würden wir einen Regressor einbeziehen, dessen Wert nur das Quadrat eines anderen Regressors ist. In diesem Fall wäre das Modell im zweiten Regressor quadratisch , wird aber dennoch als lineares Modell betrachtet, da das Modell in den Parametern immer noch linear ist ( ). ${\displaystyle {\boldsymbol {\beta}}}$

Matrix/Vektor-Formulierung

Betrachten Sie ein überbestimmtes System

${\displaystyle \sum_{j=1}^{p}X_{ij}\beta_{j}=y_{i},\ (i=1,2,\dots,n),}$

von linearen Gleichungen in unbekannten Koeffizienten , mit . (Hinweis: Bei einem linearen Modell wie oben enthalten nicht alle Elemente in Informationen zu den Datenpunkten. Die erste Spalte ist mit Einsen gefüllt, . Nur die anderen Spalten enthalten tatsächliche Daten. Hier ist also gleich die Anzahl der Regressoren plus eins. ) Dies kann in Matrixform geschrieben werden als ${\displaystyle n}$ ${\displaystyle p}$${\displaystyle \beta_{1},\beta_{2},\dots,\beta_{p}}$${\displaystyle n>p}$${\displaystyle\mathrm{X}}$${\displaystyle X_{i1}=1}$${\displaystyle p}$

${\displaystyle \mathrm{X} {\boldsymbol {\beta}}=\mathbf{y},}$

wo

${\displaystyle \mathrm {X} ={\begin{bmatrix}X_{11}&X_{12}&\cdots &X_{1p}\\X_{21}&X_{22}&\cdots &X_{2p}\\\ vdots &\vdots &\ddots &\vdots \\X_{n1}&X_{n2}&\cdots &X_{np}\end{bmatrix}},\qquad {\boldsymbol {\beta}}={\begin{bmatrix }\beta_{1}\\\beta_{2}\\\vdots \\\beta_{p}\end{bmatrix}},\qquad\mathbf{y} ={\begin{bmatrix}y_{ 1}\\y_{2}\\\vdots \\y_{n}\end{bmatrix}}.}$

Ein solches System hat in der Regel keine exakte Lösung, so das Ziel statt , die Koeffizienten zu finden ist , die die Gleichungen „beste“, im Sinne der Lösung des passen quadratischen Minimierungsproblem ${\displaystyle {\boldsymbol {\beta}}}$

${\displaystyle {\hat {\boldsymbol {\beta}}}={\underset {\boldsymbol {\beta}}{\operatorname {arg\,min} }}\,S({\boldsymbol {\beta}} ),}$

wobei die Zielfunktion gegeben ist durch ${\displaystyle S}$

${\displaystyle S({\boldsymbol {\beta}})=\sum_{i=1}^{n}{\biggl |}y_{i}-\sum_{j=1}^{p}X_ {ij}\beta_{j}{\biggr |}^{2}={\bigl\|}\mathbf {y} -\mathrm {X} {\boldsymbol {\beta}}{\bigr\|} ^{2}.}$

Eine Begründung für die Wahl dieses Kriteriums finden Sie unten in den Eigenschaften . Dieses Minimierungsproblem hat eine eindeutige Lösung, vorausgesetzt, die Spalten der Matrix sind linear unabhängig , gegeben durch das Lösen der Normalgleichungen${\displaystyle p}$${\displaystyle\mathrm{X}}$

${\displaystyle (\mathrm {X} ^{\mathrm {T}}\mathrm {X} ){\hat {\boldsymbol {\beta}}}=\mathrm {X} ^{\mathsf {T}}\ mathbf {y} \ .}$

Die Matrix ist als Gram-Matrix bekannt, und die Matrix ist als Momentenmatrix von Regressand durch Regressoren bekannt. Schließlich ist der Koeffizientenvektor der Kleinste-Quadrate- Hyperebene , ausgedrückt als ${\displaystyle \mathrm {X} ^{\mathsf {T}}\mathrm {X}}$${\displaystyle \mathrm{X}^{\mathsf{T}}\mathbf{y}}$${\displaystyle {\hat {\boldsymbol {\beta}}}}$

${\displaystyle {\hat {\boldsymbol {\beta}}}=\left(\mathrm {X} ^{\mathsf {T}}\mathrm {X} \right)^{-1}\mathrm {X} ^{\mathsf{T}}\mathbf{y}.}$

oder

${\displaystyle {\hat {\boldsymbol {\beta}}}={\boldsymbol {\beta}}+(\mathbf{X}^{\top}\mathbf{X})^{-1}\mathbf { X} ^{\top }{\boldsymbol {\varepsilon}}.}$

Einschätzung

Angenommen, b ist ein "Kandidaten"-Wert für den Parametervektor β . Die Größe y _i − x _i ^T b , Residuum für die i- te Beobachtung genannt, misst den vertikalen Abstand zwischen dem Datenpunkt ( x _i , y _i ) und der Hyperebene y = x ^T b , und bewertet damit den Grad von zwischen den tatsächlichen Daten und dem Modell passen. Die Summe der quadrierten Residuen ( SSR ) (auch Fehlerquadratsumme ( ESS ) oder Residualsumme der Quadrate ( RSS ) genannt) ist ein Maß für die Gesamtmodellanpassung:

${\displaystyle S(b)=\sum_{i=1}^{n}(y_{i}-x_{i}^{\mathrm {T}}b)^{2}=(y-Xb) ^{\mathrm {T}}(y-Xb),}$

wobei T die Matrix bezeichnet transponieren , und die Reihen von X , die Werte aller den unabhängigen Variablen assoziiert mit einem bestimmten Wert der abhängigen Variablen angibt, sind X _i = X _i ^T . Der Wert von b, der diese Summe minimiert, wird OLS-Schätzer für β genannt . Die Funktion S ( b ) ist quadratisch in b mit positiv-definitivem Hessisch , und daher besitzt diese Funktion ein eindeutiges globales Minimum bei , das durch die explizite Formel gegeben werden kann: ^[Beweis]${\displaystyle b={\hat{\beta}}}$

${\displaystyle {\hat {\beta}}=\operatorname {argmin} _{b\in\mathbb {R} ^{p}}S(b)=(X^{\mathrm {T}}X)^ {-1}X^{\mathrm {T}}y\.}$

Das Produkt N = X ^T X ist eine Gram - Matrix und ihre Inverse, Q = N ^-1 , sind die Co - Faktor - Matrix von β , eng mit seiner Kovarianzmatrix , C _β . Die Matrix ( X ^T X ) ^–1 X ^T = Q X ^T wird als Moore-Penrose-pseudoinverse Matrix von X bezeichnet. Diese Formulierung unterstreicht den Punkt, dass Schätzungen dann und nur dann durchgeführt werden können, wenn keine perfekte Multikollinearität zwischen den erklärende Variablen (die dazu führen würden, dass die Gram-Matrix keine Inverse hat).

Nachdem wir β geschätzt haben , sind die angepassten Werte (oder vorhergesagten Werte ) aus der Regression

${\displaystyle {\hat{y}}=X{\hat{\beta}}=Py,}$

wobei P = X ( X ^T X ) ⁻¹ X ^T die Projektionsmatrix auf den von den Spalten von X aufgespannten Raum V ist . Diese Matrix P wird manchmal auch als Hutmatrix bezeichnet, weil sie der Variablen y "einen Hut aufsetzt" . Ein andere Matrix, in enger Beziehung zu P ist die Auslöscher Matrix M = I _n - P ; dies ist eine Projektionsmatrix auf den Raum orthogonal zu V . Beide Matrizen P und M sind symmetrisch und idempotent (was bedeutet , dass P ² = P und M ² = M ) und an die Datenmatrix beziehen X über Identitäten PX = X und MX = 0 . Matrix M erstellt die Residuen aus der Regression:

${\displaystyle {\hat {\varepsilon}}=y-{\hat{y}}=yX{\hat{\beta}}=My=M(X\beta +\varepsilon)=(MX)\beta + M\varepsilon =M\varepsilon .}$

Unter Verwendung dieser Residuen können wir den Wert von σ ² mithilfe der reduzierten Chi-Quadrat- Statistik schätzen :

${\displaystyle s^{2}={\frac {{\hat{\varepsilon}}^{\mathrm {T} }{\hat{\varepsilon}}}{np}}={\frac {(My) ^{\mathrm {T} }My}{np}}={\frac {y^{\mathrm {T} }M^{\mathrm {T} }My}{np}}={\frac {y^ {\mathrm {T}}My}{np}}={\frac {S({\hat{\beta}})}{np}},\qquad {\hat{\sigma}}^{2}= {\frac {np}{n}}\;s^{2}}$

Der Nenner n − p sind die statistischen Freiheitsgrade . Die erste Menge, s ² ist die OLS für die Schätzung & sgr; ² , während der zweiten, ist der MLE Schätzwert für σ ² . Die beiden Schätzer sind in großen Stichproben ziemlich ähnlich; der erste Schätzer ist immer unverzerrt , während der zweite Schätzer verzerrt ist, aber einen kleineren mittleren quadratischen Fehler aufweist . In der Praxis wird s ² häufiger verwendet, da es für die Hypothesenprüfung bequemer ist. Die Quadratwurzel von s ² wird als Standardfehler der Regression , Standardfehler der Regression oder Standardfehler der Gleichung bezeichnet . ${\displaystyle \scriptstyle {\hat {\sigma}}^{2}}$

Es ist üblich, die Anpassungsgüte der OLS-Regression zu beurteilen, indem verglichen wird, um wie viel die anfängliche Variation in der Stichprobe durch Regression auf X reduziert werden kann . Das Bestimmtheitsmaß R ² ist definiert als das Verhältnis der „erklärten“ Varianz zur „gesamten“ Varianz der abhängigen Variablen y in den Fällen, in denen die Regressionsquadratsumme gleich der Summe der Residuenquadrate ist:

${\displaystyle R^{2}={\frac {\sum ({\hat{y}}_{i}-{\overline {y}})^{2}}{\sum (y_{i}- {\overline {y}})^{2}}}={\frac{y^{\mathrm {T}}P^{\mathrm {T}}LPy}{y^{\mathrm {T}}Ly }}=1-{\frac{y^{\mathrm {T}}My}{y^{\mathrm {T}}Ly}}=1-{\frac {\rm {RSS}}{\rm { TSS}}}}$

wobei TSS die Gesamtsumme der Quadrate für die abhängige Variable ist , und eine n × n- Matrix von Einsen ist. ( ist eine Zentrierungsmatrix, die der Regression auf einer Konstanten entspricht; sie subtrahiert einfach den Mittelwert von einer Variablen.) Damit R ² sinnvoll ist, muss die Matrix X der Daten zu Regressoren einen Spaltenvektor von Einsen enthalten, um die darzustellen Konstante, deren Koeffizient der Regressionsabschnitt ist. In diesem Fall ist R ² immer eine Zahl zwischen 0 und 1, wobei Werte nahe 1 einen guten Anpassungsgrad anzeigen. ${\textstyle L=I_{n}-{\frac {1}{n}}J_{n}}$${\textstyle J_{n}}$${\displaystyle L}$

Die Varianz der Vorhersage der unabhängigen Variablen als Funktion der abhängigen Variablen ist im Artikel Polynomial Least Squares angegeben .

Einfaches lineares Regressionsmodell

Enthält die Datenmatrix X nur zwei Variablen, eine Konstante und einen skalaren Regressor x _i , so wird dies als "einfaches Regressionsmodell" bezeichnet. Dieser Fall wird oft in den Statistik-Einsteigerklassen berücksichtigt, da er viel einfachere Formeln bietet, die sogar für die manuelle Berechnung geeignet sind. Die Parameter werden üblicherweise als ( α , β ) bezeichnet :

${\displaystyle y_{i}=\alpha +\beta x_{i}+\varepsilon_{i}.}$

Die Abschätzungen der kleinsten Quadrate sind in diesem Fall durch einfache Formeln gegeben

${\displaystyle {\begin{ausgerichtet}{\hat {\beta}}&={\frac {{n}\sum {x_{i}y_{i}}-\sum {x_{i}}\sum { y_{i}}}{{n}\sum {x_{i}^{2}}-(\sum {x_{i}})^{2}}}\\{\hat {\alpha}}& ={\overline{y}}-{\hat{\beta}}\,{\overline{x}}\ ,\end{ausgerichtet}}}$

Alternative Ableitungen

Im vorherigen Abschnitt wurde der Kleinste-Quadrate-Schätzer als ein Wert erhalten, der die Summe der quadrierten Residuen des Modells minimiert. Es ist jedoch auch möglich, denselben Schätzer aus anderen Ansätzen abzuleiten. In allen Fällen bleibt die Formel für den OLS-Schätzer gleich: ^{^} β = ( X ^T X ) ⁻¹ X ^T y ; der einzige Unterschied besteht darin, wie wir dieses Ergebnis interpretieren. ${\displaystyle {\hat {\beta}}}$

Projektion

Die OLS-Schätzung kann als Projektion auf den von den Regressoren aufgespannten linearen Raum betrachtet werden. (Hier bezieht sich jedes von und auf eine Spalte der Datenmatrix.)${\displaystyle X_{1}}$${\displaystyle X_{2}}$

Für Mathematiker ist OLS eine Näherungslösung für ein überbestimmtes System linearer Gleichungen Xβ ≈ y , wobei β die Unbekannte ist. Unter der Annahme, dass das System nicht exakt gelöst werden kann (die Anzahl der Gleichungen n ist viel größer als die Anzahl der Unbekannten p ), suchen wir nach einer Lösung, die die kleinste Diskrepanz zwischen der rechten und linken Seite liefert. Mit anderen Worten, wir suchen nach der Lösung, die zufriedenstellend ist

${\displaystyle {\hat{\beta}}={\rm {arg}}\min_{\beta}\,\lVert yX\beta \rVert,}$

wobei ||·|| ist die Standard- L ²  -Norm im n- dimensionalen euklidischen Raum R ⁿ . Die vorhergesagte Größe Xβ ist nur eine bestimmte Linearkombination der Vektoren von Regressoren. Somit ist der Restvektor y - Xβ hat die kleinste Länge , wenn y ist orthogonal projiziert auf den linearen Unterraum aufgespannt durch die Spalten von X . Der OLS-Schätzer kann in diesem Fall als Koeffizienten der Vektorzerlegung von ^{^} y = Py entlang der Basis von X interpretiert werden . ${\displaystyle {\hat {\beta}}}$

Mit anderen Worten, die Gradientengleichungen im Minimum können wie folgt geschrieben werden:

${\displaystyle (\mathbf{y} -X{\hat {\boldsymbol {\beta}}})^{\rm {T}}X=0.}$

Eine geometrische Interpretation dieser Gleichungen ist, dass der Vektor der Residuen orthogonal zum Spaltenraum von X ist , da das Skalarprodukt für jeden konformen Vektor v gleich Null ist . Dies bedeutet, dass dies der kürzeste aller möglichen Vektoren ist , d. h. die Varianz der Residuen ist die minimal mögliche. Dies ist rechts dargestellt. ${\displaystyle \mathbf{y} -X{\hat {\boldsymbol {\beta}}}}$${\displaystyle (\mathbf{y} -X{\hat{\boldsymbol {\beta}}})\cdot X\mathbf{v}}$${\displaystyle \mathbf{y} -X{\boldsymbol {\hat {\beta}}}}$${\displaystyle \mathbf{y} -X{\boldsymbol {\beta}}}$

Unter Einführung einer Matrix K mit der Annahme, dass eine Matrix nicht singulär ist und K ^T X = 0 (vgl. Orthogonale Projektionen ), sollte der Restvektor die folgende Gleichung erfüllen: ${\displaystyle {\hat {\boldsymbol {\gamma}}}}$${\displaystyle [X\ K]}$

${\displaystyle {\hat {\mathbf{r}}}\triangleq\mathbf{y} -X{\hat {\boldsymbol {\beta}}}}=K{\hat {\boldsymbol {\gamma}}}. }$

Die Gleichung und Lösung der linearen kleinsten Quadrate werden somit wie folgt beschrieben:

${\displaystyle \mathbf {y} ={\begin{bmatrix}X&K\end{bmatrix}}{\begin{pmatrix}{\hat {\boldsymbol {\beta}}}\\{\hat {\boldsymbol {\ gamma }}}\end{pmatrix}},}$

${\displaystyle {\begin{pmatrix}{\hat {\boldsymbol {\beta}}}\\{\hat {\boldsymbol {\gamma}}}\end{pmatrix}}={\begin{bmatrix}X&K\ end{bmatrix}}^{-1}\mathbf{y} ={\begin{bmatrix}(X^{\rm {T}}X)^{-1}X^{\rm {T}}\\ (K^{\rm{T}}K)^{-1}K^{\rm{T}}\end{bmatrix}}\mathbf{y} .}$

Eine andere Betrachtungsweise besteht darin, die Regressionslinie als einen gewichteten Durchschnitt der Linien zu betrachten, die durch die Kombination von zwei beliebigen Punkten im Datensatz verlaufen. Obwohl diese Art der Berechnung rechenintensiver ist, bietet sie eine bessere Intuition für OLS.

Maximale Wahrscheinlichkeit

Der OLS-Schätzer ist unter der Normalitätsannahme für die Fehlerterme identisch mit dem Maximum-Likelihood-Schätzer (MLE). ^[Beweis] Diese Normalitätsannahme hat historische Bedeutung, da sie die Grundlage für die frühen Arbeiten zur linearen Regressionsanalyse von Yule und Pearson lieferte . Aus den Eigenschaften von MLE können wir schließen, dass der OLS-Schätzer asymptotisch effizient ist (im Sinne des Erreichens der Cramér-Rao-Schranke für die Varianz), wenn die Normalitätsannahme erfüllt ist.

Verallgemeinerte Methode der Momente

Im iid Fall kann der OLS-Schätzer auch als GMM- Schätzer betrachtet werden, der sich aus den Momentbedingungen ergibt

${\displaystyle \mathrm {E} {\big [}\,x_{i}(y_{i}-x_{i}^{T}\beta)\,{\big]}=0.}$

Diese Momentbedingungen geben an, dass die Regressoren nicht mit den Fehlern korreliert sein sollten. Da x _i ein p- Vektor ist, ist die Anzahl der Momentenbedingungen gleich der Dimension des Parametervektors β und somit ist das System exakt identifiziert. Dies ist der sogenannte klassische GMM-Fall, bei dem der Schätzer nicht von der Wahl der Gewichtungsmatrix abhängt.

Beachten Sie, dass die ursprüngliche strenge Exogenitätsannahme E[ ε _i  | x _i ] = 0 impliziert einen weitaus reichhaltigeren Satz von Momentbedingungen als oben angegeben. Insbesondere bedeutet diese Annahme , dass für jeden Vektor-Funktion ƒ , die Moment Bedingung E [ ƒ ( x _i ) · ε _i ] = 0 halten wird. Mit dem Gauß-Markov-Theorem kann jedoch gezeigt werden, dass die optimale Wahl der Funktion ƒ darin besteht, ƒ ( x ) = x zu nehmen , was zu der oben angegebenen Momentengleichung führt.

Eigenschaften

Annahmen

Es gibt mehrere verschiedene Rahmen, in denen das lineare Regressionsmodell gegossen werden kann, um die OLS-Technik anwendbar zu machen. Jede dieser Einstellungen erzeugt dieselben Formeln und dieselben Ergebnisse. Der einzige Unterschied besteht in der Interpretation und den Annahmen, die gemacht werden müssen, damit die Methode aussagekräftige Ergebnisse liefert. Die Wahl des anwendbaren Rahmens hängt hauptsächlich von der Art der vorliegenden Daten und der durchzuführenden Inferenzaufgabe ab.

Einer der Unterschiede bei der Interpretation besteht darin, ob die Regressoren als Zufallsvariablen oder als vordefinierte Konstanten behandelt werden. Im ersten Fall ( zufälliges Design ) sind die Regressoren x _i zufällig und werden wie in einer Beobachtungsstudie zusammen mit den y _i aus einer Population ausgewählt . Dieser Ansatz ermöglicht eine natürlichere Untersuchung der asymptotischen Eigenschaften der Schätzer. In der anderen Auslegung ( festes Design ), die Regressoren X sind bekannt als Konstanten gesetzt durch einen behandelten Design und y bedingt auf den Werten der abgetasteten X wie in einem Experiment . Für praktische Zwecke ist diese Unterscheidung oft unwichtig, da Schätzung und Inferenz während der Konditionierung auf X durchgeführt werden . Alle in diesem Artikel angegebenen Ergebnisse liegen innerhalb des Random-Design-Rahmens.

Klassisches lineares Regressionsmodell

Das klassische Modell konzentriert sich auf die "Finite Sample"-Schätzung und Inferenz, was bedeutet, dass die Anzahl der Beobachtungen n fest ist. Dies steht im Gegensatz zu den anderen Ansätzen, die das asymptotische Verhalten von OLS untersuchen und bei denen die Anzahl der Beobachtungen ins Unendliche wachsen darf.

• Richtige Spezifikation . Die lineare Funktionsform muss mit der Form des eigentlichen datenerzeugenden Prozesses übereinstimmen.
• Strenge Exogenität . Die Fehler in der Regression sollten den bedingten Mittelwert Null haben:

  ${\displaystyle \operatorname {E} [\,\varepsilon \mid X\,]=0.}$

Die unmittelbare Folge der Exogenität Annahme ist , dass die Fehler haben mittlere Null: E [ ε ] = 0 , und dass die Regressoren unkorreliert sind mit den Fehlern: E [ X ^T ε ] = 0 .

Die Annahme der Exogenität ist für die OLS-Theorie entscheidend. Wenn dies zutrifft, werden die Regressorvariablen als exogen bezeichnet . Ist dies nicht der Fall, werden die mit dem Fehlerterm korrelierten Regressoren als endogen bezeichnet und die OLS-Schätzungen werden ungültig. In einem solchen Fall kann die Methode der instrumentellen Variablen verwendet werden, um eine Inferenz durchzuführen.

• Keine lineare Abhängigkeit . Die Regressoren in X müssen alle linear unabhängig sein . Mathematisch bedeutet dies, dass die Matrix X fast sicher den vollen Spaltenrang haben muss :

  ${\displaystyle \Pr\!{\big [}\,\operatorname {Rang} (X)=p\,{\big]}=1.}$

Üblicherweise wird auch angenommen, dass die Regressoren bis mindestens zum zweiten Moment endliche Momente haben. Dann ist die Matrix Q _xx = E[ X ^T X  /  n ] endlich und positiv semi-definit.

Wenn diese Annahme verletzt wird, werden die Regressoren als linear abhängig oder perfekt multikollinear bezeichnet . In einem solchen Fall kann der Wert des Regressionskoeffizienten β nicht gelernt werden, obwohl die Vorhersage von y- Werten für neue Werte der Regressoren, die in demselben linear abhängigen Unterraum liegen, immer noch möglich ist.

• Sphärische Fehler :

  ${\displaystyle \operatorname {Var} [\,\varepsilon \mid X\,]=\sigma ^{2}I_{n},}$

wobei I _n ist die Identitätsmatrix der Dimension n und σ ² ein Parameter ist , die die Varianz von jeder Beobachtung bestimmt. Dieser σ ² wird im Modell als störender Parameter betrachtet , obwohl er normalerweise auch geschätzt wird. Wenn diese Annahme verletzt wird, sind die OLS-Schätzungen noch gültig, aber nicht mehr effizient.

Es ist üblich, diese Annahme in zwei Teile aufzuteilen:

• Homoskedastizität : E[  ε _i ²  | X  ] = σ ² , was bedeutetdaß der Fehlerterm die gleiche Varianz σ ² in jeder Beobachtung. Wenn diese Anforderung verletzt wird, wird dies als Heteroskedastizität bezeichnet , in einem solchen Fall wäre ein effizienterer Schätzer die gewichtete Methode der kleinsten Quadrate . Wenn die Fehler eine unendliche Varianz haben, haben die OLS-Schätzungen ebenfalls eine unendliche Varianz (obwohl sie nach dem Gesetz der großen Zahlen dennoch zu den wahren Werten tendieren, solange die Fehler den Mittelwert Null haben). In diesem Fall werden robuste Schätztechniken empfohlen.
• Keine Autokorrelation : die Fehler sind zwischen den Beobachtungen unkorreliert : E[  ε _i ε _j  | X  ] = 0 für i ≠ j . Diese Annahme kann im Kontext von Zeitreihendaten , Paneldaten , Clusterstichproben, hierarchischen Daten, Messwiederholungsdaten, Längsschnittdaten und anderen Daten mit Abhängigkeiten verletzt werden . In solchen Fällen bietet die verallgemeinerte Methode der kleinsten Quadrate eine bessere Alternative als die OLS. Ein anderer Ausdruck für Autokorrelation ist serielle Korrelation .

• Normalität . Manchmal wird zusätzlich angenommen, dass die Fehler eine von den Regressoren bedingte Normalverteilung haben :

  ${\displaystyle \varepsilon\mid X\sim {\mathcal{N}}(0,\sigma^{2}I_{n}).}$

Diese Annahme ist für die Gültigkeit der OLS-Methode nicht erforderlich, obwohl in diesem Fall bestimmte zusätzliche endliche Stichprobeneigenschaften festgestellt werden können (insbesondere im Bereich der Hypothesenprüfung). Auch wenn die Fehler normal sind, entspricht der OLS-Schätzer dem Maximum-Likelihood-Schätzer (MLE) und ist daher in der Klasse aller regulären Schätzer asymptotisch effizient . Wichtig ist, dass die Normalitätsannahme nur für die Fehlerterme gilt; Entgegen einem weit verbreiteten Missverständnis muss die (abhängige) Variable der Antwort nicht normalverteilt sein.

Unabhängig und identisch verteilt (iid)

Bei einigen Anwendungen, insbesondere bei Querschnittsdaten , wird zusätzlich angenommen, dass alle Beobachtungen unabhängig und identisch verteilt sind. Dies bedeutet, dass alle Beobachtungen einer Zufallsstichprobe entnommen werden , was alle zuvor aufgeführten Annahmen einfacher und leichter interpretierbar macht. Auch dieser Rahmen erlaubt es, asymptotische Ergebnisse (als Stichprobengröße n  → ∞ ) anzugeben, die als theoretische Möglichkeit verstanden werden, neue unabhängige Beobachtungen aus dem Datengenerierungsprozess zu holen . Die Liste der Annahmen in diesem Fall lautet:

• iid Beobachtungen : ( x _i , y _i ) ist unabhängig von und hat die gleiche Verteilung wie ( x _j , y _j ) für alle i j ;
• keine perfekte Multikollinearität : Q _xx = E[  x _i  x _i ^T  ] ist eine positiv-definite Matrix ;
• Exogenität : E[  ε _i  | x _i  ] = 0;
• Homoskedastizität : Var[  ε _i  | x _i  ] = σ ² .

Zeitreihenmodell

• Der stochastische Prozess { x _i , y _i } ist stationär und ergodische ; Wenn { x _i , y _i } nicht stationär ist, sind OLS-Ergebnisse oft falsch, es sei denn, { x _i , y _i } ist kointegrierend .
• Die Regressoren werden vorbestimmte : E [ x _i ε _i ] = 0 für alle i = 1, ..., n ;
• Die p × p- Matrix Q _xx = E[  x _i  x _i ^T  ] hat vollen Rang und ist daher positiv-definit ;
• { x _i ε _i } ist eine Martingaldifferenzenfolge mit einer endlichen Matrix von zweiten Momenten Q _{xxε ²} = E[  ε _i ² x _i  x _i ^T  ] .

Endliche Probeneigenschaften

Vor allem unter der strengen Exogenität Annahme des OLS Schätzer und s ² sind unvoreingenommene , was bedeutet , dass ihre Erwartungswerte mit den wahren Werten der Parameter übereinstimmen: ^[Test]${\displaystyle \scriptstyle {\hat {\beta}}}$

${\displaystyle \operatorname {E} [\,{\hat {\beta}}\mid X\,]=\beta ,\quad \operatorname {E} [\,s^{2}\mid X\,] =\sigma^{2}.}$

Wenn die strikte Exogenität nicht gilt (wie es bei vielen Zeitreihenmodellen der Fall ist , in denen Exogenität nur in Bezug auf vergangene Schocks angenommen wird, aber nicht auf zukünftige), dann werden diese Schätzer in endlichen Stichproben verzerrt.

Die Varianz-Kovarianz-Matrix (oder einfach Kovarianz-Matrix ) von ist gleich ${\displaystyle \scriptstyle {\hat {\beta}}}$

${\displaystyle \operatorname {Var} [\,{\hat {\beta}}\mid X\,]=\sigma ^{2}(X^{T}X)^{-1}=\sigma ^{ 2}F.}$

Insbesondere ist der Standardfehler jedes Koeffizienten gleich der Quadratwurzel des j- ten diagonalen Elements dieser Matrix. Die Schätzung dieses Standardfehlers wird erhalten, indem die unbekannte Größe σ ² durch ihre Schätzung s ^{2 ersetzt wird} . Daher, ${\displaystyle \scriptstyle {\hat {\beta}}_{j}}$

${\displaystyle {\widehat {\operatorname {s.\!e.} }}({\hat {\beta}}_{j})={\sqrt {s^{2}(X^{T}X )_{jj}^{-1}}}}$

Es kann auch leicht gezeigt werden, dass der Schätzer nicht mit den Residuen aus dem Modell korreliert: ${\displaystyle \scriptstyle {\hat {\beta}}}$

${\displaystyle \operatorname {Cov} [\,{\hat {\beta}},{\hat {\varepsilon}}\mid X\,]=0.}$

Der Satz von Gauss-Markov besagt, dass unter der Annahme sphärischer Fehler (d. h. die Fehler sollten unkorreliert und homoskedastisch sein ) der Schätzer in der Klasse der linearen erwartungsfreien Schätzer effizient ist. Dies wird als bester linearer unverzerrter Schätzer (BLUE) bezeichnet. Die Effizienz sollte so verstanden werden, als ob wir einen anderen Schätzer finden würden, der in y linear und unverzerrt wäre, dann ${\displaystyle \scriptstyle {\hat {\beta}}}$${\displaystyle \scriptstyle {\tilde {\beta}}}$

${\displaystyle \operatorname {Var} [\,{\tilde {\beta}}\mid X\,]-\operatorname {Var} [\,{\hat {\beta}}\mid X\,]\geq 0}$

in dem Sinne, dass dies eine nichtnegativ-bestimmte Matrix ist . Dieser Satz stellt Optimalität nur in der Klasse der linearen erwartungsfreien Schätzer her, was ziemlich restriktiv ist. Abhängig von der Verteilung der Fehlerterme ε können andere, nichtlineare Schätzer bessere Ergebnisse als OLS liefern.

Normalität vorausgesetzt

Die bisher aufgeführten Eigenschaften sind alle unabhängig von der zugrunde liegenden Verteilung der Fehlerterme gültig. Wenn Sie jedoch bereit sind , anzunehmen , dass die Normalitätsannahme gilt (das heißt, dass ε ~ N (0, σ ² I _n ) ), dann weitere Eigenschaften der OLS Schätzer kann festgestellt werden.

Der Schätzer ist normalverteilt, mit Mittelwert und Varianz wie oben angegeben: ${\displaystyle \scriptstyle {\hat {\beta}}}$

${\displaystyle {\hat{\beta}}\\sim\{\mathcal{N}}{\big(}\beta,\\sigma^{2}(X^{\mathrm {T}}X)^ {-1}{\big)}}$

wobei Q die Kofaktormatrix ist . Dieser Schätzer erreicht die Cramér-Rao-Schranke für das Modell und ist somit in der Klasse aller unverzerrten Schätzer optimal. Beachten Sie, dass dieses Ergebnis im Gegensatz zum Gauss-Markov-Theorem die Optimalität sowohl zwischen linearen als auch nichtlinearen Schätzern herstellt, jedoch nur im Fall normalverteilter Fehlerterme.

Der Schätzer s ² ist proportional zur Chi-Quadrat-Verteilung :

${\displaystyle s^{2}\ \sim \ {\frac {\sigma^{2}}{np}}\cdot \chi_{np}^{2}}$

Die Varianz dieses Schätzers ist gleich 2 σ ⁴ /( n  −  p ) , was die Cramér-Rao-Schranke von 2 σ ⁴ / n nicht erreicht . Es wurde jedoch gezeigt, dass es keine unverzerrten Schätzer von σ ² mit einer kleineren Varianz als der des Schätzers s ^{2 gibt} . Wenn wir bereit sind, verzerrte Schätzer zuzulassen und die Klasse von Schätzern zu berücksichtigen, die proportional zur Summe der quadrierten Residuen (SSR) des Modells sind, dann ist der beste (im Sinne des mittleren quadratischen Fehlers ) Schätzer in dieser Klasse ^~ σ ² = SSR  /  ( n  −  p  + 2) , was sogar die Cramér-Rao-Schranke übertrifft, falls nur ein Regressor vorhanden ist ( p = 1 ).

Darüber hinaus sind die Schätzer und s ² sind unabhängig , die Tatsache , die in den nützlichen kommt , wenn für die Regression der t- und F-Tests zu konstruieren. ${\displaystyle \scriptstyle {\hat {\beta}}}$

Einflussreiche Beobachtungen

Wie bereits erwähnt, ist der Schätzer in y linear , dh er repräsentiert eine Linearkombination der abhängigen Variablen y _i . Die Gewichte in dieser Linearkombination sind Funktionen der Regressoren X und im Allgemeinen ungleich. Die Beobachtungen mit hoher Gewichtung werden als einflussreich bezeichnet, weil sie einen stärkeren Einfluss auf den Wert des Schätzers haben. ${\displaystyle {\hat {\beta}}}$

Um zu analysieren, welche Beobachtungen einflussreich sind, entfernen wir eine bestimmte j- te Beobachtung und überlegen, wie stark sich die geschätzten Mengen ändern werden (ähnlich der Jackknife-Methode ). Es kann gezeigt werden, dass die Änderung des OLS-Schätzers für β gleich ist

${\displaystyle {\hat{\beta}}^{(j)}-{\hat{\beta}}=-{\frac {1}{1-h_{j}}}(X^{\mathrm { T} }X)^{-1}x_{j}^{\mathrm{T}}{\hat{\varepsilon}}_{j}\,,}$

wobei h _j = x _j ^T  ( X ^T X ) ^–1 x _j das j- te diagonale Element der Hutmatrix P ist und x _j der Vektor der Regressoren ist, die der j- ten Beobachtung entsprechen. In ähnlicher Weise ist die Änderung des vorhergesagten Werts für die j- te Beobachtung, die sich aus dem Weglassen dieser Beobachtung aus dem Datensatz ergibt, gleich

${\displaystyle {\hat{y}}_{j}^{(j)}-{\hat{y}}_{j}=x_{j}^{\mathrm {T} }{\hat {\ beta }}^{(j)}-x_{j}^{T}{\hat{\beta}}=-{\frac {h_{j}}{1-h_{j}}}\,{\ Hut {\varepsilon}}_{j}}$

Aus den Eigenschaften der Hutmatrix ist 0 h _j ≤ 1 , und sie summieren sich zu p , so dass im Durchschnitt h _j ≈ p/n . Diese Größen h _j werden Leverage genannt , und Beobachtungen mit hohem h _j werden Leverage Points genannt . Normalerweise sollten die Beobachtungen mit hohem Leverage genauer überprüft werden, falls sie fehlerhaft sind, Ausreißer oder auf andere Weise untypisch für den Rest des Datensatzes sind.

Partitionierte Regression

Manchmal lassen sich die Variablen und entsprechenden Parameter in der Regression logisch in zwei Gruppen aufteilen, sodass die Regression Form annimmt

${\displaystyle y=X_{1}\beta_{1}+X_{2}\beta_{2}+\varepsilon,}$

wobei X ₁ und X ₂ haben Abmessungen n × p ₁ , n × p ₂ und β ₁ , β ₂ sind p ₁ × 1 und p ₂ × 1 - Vektoren, mit p ₁ + p ₂ = p .

Das Frisch-Waugh-Lovell-Theorem besagt, dass in dieser Regression die Residuen und die OLS-Schätzung numerisch identisch mit den Residuen und der OLS-Schätzung für β ₂ in der folgenden Regression sind: ${\displaystyle {\hat {\varepsilon}}}$${\displaystyle \scriptstyle {\hat {\beta}}_{2}}$

${\displaystyle M_{1}y=M_{1}X_{2}\beta_{2}+\eta\,,}$

wobei M ₁ die Annihilatormatrix für Regressoren X _{1 ist} .

Das Theorem kann verwendet werden, um eine Reihe von theoretischen Ergebnissen zu erhalten. Zum Beispiel ist eine Regression mit einer Konstanten und einem anderen Regressor gleichbedeutend damit, den Mittelwert von der abhängigen Variablen und dem Regressor zu subtrahieren und dann die Regression für die de-meaned Variablen auszuführen, jedoch ohne den konstanten Term.

Eingeschränkte Schätzung

Angenommen, es ist bekannt, dass die Koeffizienten in der Regression ein lineares Gleichungssystem erfüllen

${\displaystyle A\colon \quad Q^{T}\beta =c,\,}$

wobei Q eine p × q- Matrix mit vollem Rang ist und c ein q × 1-Vektor bekannter Konstanten ist, wobei q < p ist . In diesem Fall entspricht die Schätzung der kleinsten Quadrate der Minimierung der Summe der quadrierten Residuen des Modells, das der Einschränkung A unterliegt . Der Constrained Least Squares (CLS) -Schätzer kann durch eine explizite Formel angegeben werden:

${\displaystyle {\hat{\beta}}^{c}={\hat{\beta}}-(X^{T}X)^{-1}Q{\Big (}Q^{T}( X^{T}X)^{-1}Q{\Big)}^{-1}(Q^{T}{\hat{\beta}}-c).}$

Dieser Ausdruck für den eingeschränkten Schätzer ist gültig, solange die Matrix X ^T X invertierbar ist. Zu Beginn dieses Artikels wurde angenommen, dass diese Matrix den vollen Rang hat, und es wurde darauf hingewiesen, dass β nicht identifizierbar ist , wenn die Rangbedingung fehlschlägt . Allerdings kann es vorkommen , dass die Beschränkung Zugabe von A Fabrikate β erkennbar, wobei in diesem Fall möchte man die Formel für den Schätzer finden. Der Schätzer ist gleich

${\displaystyle {\hat{\beta}}^{c}=R(R^{T}X^{T}XR)^{-1}R^{T}X^{T}y+{\Big ( }I_{p}-R(R^{T}X^{T}XR)^{-1}R^{T}X^{T}X{\Big )}Q(Q^{T}Q) ^{-1}c,}$

wobei R eine p ×( p  −  q )-Matrix ist, so dass die Matrix [ QR ] nicht singulär ist und R ^T Q = 0 . Eine solche Matrix kann immer gefunden werden, obwohl sie im Allgemeinen nicht eindeutig ist. Die zweite Formel stimmt mit der ersten überein, wenn X ^T X invertierbar ist.

Große Probeneigenschaften

Die Kleinste-Quadrate-Schätzer sind Punktschätzungen der linearen Regressionsmodellparameter β . Im Allgemeinen möchten wir jedoch auch wissen, wie nahe diese Schätzungen an den wahren Werten der Parameter liegen. Mit anderen Worten, wir wollen die Intervallschätzungen konstruieren .

Da wir keine Annahme über die Verteilung des Fehlerterms ε _{i gemacht haben} , ist es unmöglich, auf die Verteilung der Schätzer und zu schließen . Dennoch können wir den zentralen Grenzwertsatz anwenden , um ihre asymptotischen Eigenschaften abzuleiten, wenn die Stichprobengröße n gegen Unendlich geht. Obwohl die Stichprobengröße notwendigerweise endlich ist, ist es üblich, anzunehmen, dass n "groß genug" ist, damit die wahre Verteilung des OLS-Schätzers nahe an seiner asymptotischen Grenze liegt. ${\displaystyle {\hat {\beta}}}$${\displaystyle {\hat {\sigma}}^{2}}$

Wir können zeigen , dass unter den Modellannahmen, die der kleinsten Quadrate Schätzer für β ist konsistent (dh konvergiert in Wahrscheinlichkeit zu β ) und asymptotisch normal: ^[Test]${\displaystyle {\hat {\beta}}}$

${\displaystyle ({\hat{\beta}}-\beta)\ {\xrightarrow {d}}\ {\mathcal {N}}{\big (}0,\;\sigma ^{2}Q_{xx }^{-1}{\big)},}$

wo ${\displaystyle Q_{xx}=X^{T}X.}$

Intervalle

Unter Verwendung dieser asymptotischen Verteilung können ungefähre zweiseitige Konfidenzintervalle für die j- te Komponente des Vektors konstruiert werden als ${\displaystyle {\hat {\beta}}}$

${\displaystyle \beta_{j}\in {\bigg[}\ {\hat{\beta}}_{j}\pm q_{1-{\frac {\alpha}{2}}}^{{ \mathcal{N}}(0,1)}\!{\sqrt {{\hat{\sigma}}^{2}\left[Q_{xx}^{-1}\right]_{jj}} }\ {\bigg ]}}$   beim Konfidenzniveau 1 −  α ,

wobei q die Quantilfunktion der Standardnormalverteilung bezeichnet und [·] _jj das j- te Diagonalelement einer Matrix ist.

In ähnlicher Weise ist auch der Kleinste-Quadrate-Schätzer für σ ² konsistent und asymptotisch normal (vorausgesetzt, das vierte Moment von ε _i existiert) mit Grenzverteilung

${\displaystyle ({\hat{\sigma}}^{2}-\sigma^{2})\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\operatorname { E} \left[\varepsilon_{i}^{4}\right]-\sigma^{4}\right).}$

Diese asymptotischen Verteilungen können zur Vorhersage, zum Testen von Hypothesen, zum Konstruieren anderer Schätzer usw. verwendet werden. Betrachten Sie als Beispiel das Problem der Vorhersage. Angenommen, es liegt ein Punkt innerhalb des Verteilungsbereichs der Regressoren, und man möchte wissen, wie die Antwortvariable an diesem Punkt gewesen wäre. Die mittlere Antwort ist die Menge , während die vorhergesagte Antwort ist . Offensichtlich ist die vorhergesagte Antwort eine Zufallsvariable, ihre Verteilung kann abgeleitet werden von : ${\displaystyle x_{0}}$${\displaystyle y_{0}=x_{0}^{\mathrm {T}}\beta}$${\displaystyle {\hat {y}}_{0}=x_{0}^{\mathrm {T} }{\hat {\beta}}}$${\displaystyle {\hat {\beta}}}$

${\displaystyle \left({\hat{y}}_{0}-y_{0}\right)\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\sigma ^{2}x_{0}^{\mathrm {T}}Q_{xx}^{-1}x_{0}\right),}$

Dies ermöglicht die Konstruktion von Konfidenzintervallen für die mittlere Antwort : ${\displaystyle y_{0}}$

${\displaystyle y_{0}\in \left[\x_{0}^{\mathrm {T} }{\hat {\beta}}\pm q_{1-{\frac {\alpha}{2}} }^{{\mathcal{N}}(0,1)}\!{\sqrt {{\hat{\sigma}}^{2}x_{0}^{\mathrm {T}}Q_{xx} ^{-1}x_{0}}}\ \right]}$   auf dem Konfidenzniveau 1 −  α .

Hypothesentest

Zwei Hypothesentests werden besonders häufig verwendet. Zunächst möchte man wissen, ob die geschätzte Regressionsgleichung besser ist, als einfach vorherzusagen, dass alle Werte der Antwortvariablen ihrem Stichprobenmittelwert entsprechen (wenn nicht, hat sie keine Erklärungskraft). Die Nullhypothese ohne Erklärungswert der geschätzten Regression wird mit einem F-Test getestet . Wenn sich herausstellt, dass der berechnete F-Wert groß genug ist, um seinen kritischen Wert für das vorgewählte Signifikanzniveau zu überschreiten, wird die Nullhypothese verworfen und die Alternativhypothese , dass die Regression Erklärungskraft hat, akzeptiert. Andernfalls wird die Nullhypothese ohne Erklärungskraft akzeptiert.

Zweitens möchte man für jede interessierende erklärende Variable wissen, ob ihr geschätzter Koeffizient signifikant von Null abweicht – das heißt, ob diese bestimmte erklärende Variable tatsächlich eine Aussagekraft bei der Vorhersage der Antwortvariablen hat. Hier lautet die Nullhypothese, dass der wahre Koeffizient null ist. Diese Hypothese wird getestet, indem die t-Statistik des Koeffizienten als das Verhältnis der Koeffizientenschätzung zu seinem Standardfehler berechnet wird . Wenn die t-Statistik größer als ein vorbestimmter Wert ist, wird die Nullhypothese verworfen und es wird festgestellt, dass die Variable eine Erklärungskraft hat, wobei ihr Koeffizient signifikant von Null verschieden ist. Andernfalls wird die Nullhypothese eines Nullwerts des wahren Koeffizienten akzeptiert.

Darüber hinaus wird der Chow-Test verwendet, um zu testen, ob zwei Unterabtastwerte beide die gleichen zugrundeliegenden wahren Koeffizientenwerte aufweisen. Die Summe der quadrierten Regressionsresiduen auf jeder der Teilmengen und auf dem kombinierten Datensatz wird durch Berechnen einer F-Statistik verglichen; wenn dieser einen kritischen Wert überschreitet, wird die Nullhypothese von keinem Unterschied zwischen den beiden Teilmengen verworfen; andernfalls wird es akzeptiert.

Beispiel mit echten Daten

Streudiagramm der Daten, die Beziehung ist leicht gekrümmt, aber nahezu linear

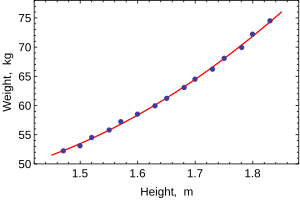
Der folgende Datensatz gibt durchschnittliche Größen und Gewichte für amerikanische Frauen im Alter von 30–39 Jahren an (Quelle: The World Almanac and Book of Facts, 1975 ).

Höhe (m)	1,47	1,50	1,52	1,55	1,57	1,60	1.63	1.65	1,68	1,70	1,73	1,75	1,78	1,80	1,83
Gewicht (kg)	52,21	53,12	54,48	55,84	57,20	58,57	59,93	61,29	63,11	64,47	66,28	68,10	69,92	72,19	74,46

Wenn nur eine abhängige Variable modelliert wird, schlägt ein Streudiagramm die Form und Stärke der Beziehung zwischen der abhängigen Variablen und den Regressoren vor. Es kann auch Ausreißer, Heteroskedastizität und andere Aspekte der Daten aufdecken, die die Interpretation eines angepassten Regressionsmodells erschweren können. Das Streudiagramm legt nahe, dass die Beziehung stark ist und als quadratische Funktion angenähert werden kann. OLS kann mit nichtlinearen Beziehungen umgehen, indem es den Regressor HEIGHT ² einführt . Das Regressionsmodell wird dann zu einem multiplen linearen Modell:

${\displaystyle w_{i}=\beta_{1}+\beta_{2}h_{i}+\beta_{3}h_{i}^{2}+\varepsilon_{i}.}$

Angepasste Regression

Die Ausgabe der gängigsten Statistikpakete sieht so aus:

Methode	Kleinsten Quadrate
Abhängige Variable	LAST
Beobachtungen	fünfzehn
Parameter	Wert	Standardfehler	t-Statistik	p-Wert
${\displaystyle \beta_{1}}$	128.8128	16.3083	7,8986	0.0000
${\displaystyle \beta_{2}}$	–143,1620	19.8332	–7.2183	0.0000
${\displaystyle \beta_{3}}$	61.9603	6.0084	10.3122	0.0000
R 2	0.9989	SE der Regression		0,2516
Angepasstes R 2	0.9987	Modell-Quadratmeter		692.61
Log-Wahrscheinlichkeit	1.0890	Restsumme von qm		0.7595
Durbin-Watson-Statistik.	2.1013	Gesamtsumme der Quadratmeter		693.37
Akaike-Kriterium	0,2548	F-Statistik		5471.2
Schwarz-Kriterium	0,3964	p-Wert (F-Stat)		0.0000

In dieser Tabelle:

• Die Spalte Wert enthält die Schätzungen der kleinsten Quadrate der Parameter β _j
• Die Spalte Std error zeigt die Standardfehler jeder Koeffizientenschätzung:${\displaystyle {\hat {\sigma}}_{j}=\left({\hat{\sigma}}^{2}\left[Q_{xx}^{-1}\right]_{jj} \right)^{\frac {1}{2}}}$
• Die Spalten t-Statistik und p-Wert testen, ob einer der Koeffizienten gleich Null sein könnte. Die t- Statistik wird einfach als berechnet . Wenn die Fehler ε einer Normalverteilung folgen, folgt t einer Student-t-Verteilung. Unter schwächeren Bedingungen ist t asymptotisch normal. Große Werte von t zeigen an, dass die Nullhypothese abgelehnt werden kann und der entsprechende Koeffizient nicht Null ist. Die zweite Spalte, p- Wert , drückt die Ergebnisse des Hypothesentests als Signifikanzniveau aus . Herkömmlicherweise werden p- Werte kleiner als 0,05 als Beweis dafür angesehen, dass der Populationskoeffizient nicht null ist.${\displaystyle t={\hat {\beta}}_{j}/{\hat {\sigma}}_{j}}$
• R-Quadrat ist das Bestimmtheitsmaß , das die Anpassungsgüte der Regression angibt. Diese Statistik ist gleich Eins, wenn die Anpassung perfekt ist, und Null, wenn die Regressoren X keinerlei Erklärungskraft haben. Dies ist eine verzerrte Schätzung des R-Quadrats der Grundgesamtheit und wird niemals abnehmen, wenn zusätzliche Regressoren hinzugefügt werden, selbst wenn sie irrelevant sind.
• Angepasstes R-Quadrat ist eine leicht modifizierte Version von , entworfen, um die überschüssige Anzahl von Regressoren zu bestrafen, die nicht zur Erklärungskraft der Regression beitragen. Diese Statistik ist immer kleiner als , kann abnehmen, wenn neue Regressoren hinzugefügt werden, und bei schlecht passenden Modellen sogar negativ sein:${\displaystyle R^{2}}$${\displaystyle R^{2}}$

${\displaystyle {\overline {R}}^{2}=1-{\frac {n-1}{np}}(1-R^{2})}$

• Die Log-Likelihood wird unter der Annahme berechnet, dass die Fehler der Normalverteilung folgen. Auch wenn die Annahme nicht sehr vernünftig ist, kann diese Statistik dennoch bei der Durchführung von LR-Tests Verwendung finden.
• Die Durbin-Watson-Statistik testet, ob es Hinweise auf eine serielle Korrelation zwischen den Residuen gibt. Als Faustregel gilt, dass ein Wert kleiner als 2 ein Hinweis auf eine positive Korrelation ist.
• Sowohl das Akaike-Informationskriterium als auch das Schwarz-Kriterium werden für die Modellauswahl verwendet. Im Allgemeinen weisen beim Vergleich zweier alternativer Modelle kleinere Werte eines dieser Kriterien auf ein besseres Modell hin.
• Der Standardfehler der Regression ist eine Schätzung von σ , dem Standardfehler des Fehlerterms.
• Die Gesamtsumme der Quadrate , die Modellsumme der Quadrate und die Restsumme der Quadrate sagen uns, wie viel der anfänglichen Variation in der Stichprobe durch die Regression erklärt wurde.
• Die F-Statistik versucht, die Hypothese zu testen, dass alle Koeffizienten (außer dem Achsenabschnitt) gleich Null sind. Diese Statistik hat eine F ( p–1 , n–p )-Verteilung unter der Nullhypothese und der Normalitätsannahme, und ihr p-Wert zeigt die Wahrscheinlichkeit an, dass die Hypothese tatsächlich wahr ist. Beachten Sie, dass diese Statistik ungültig wird, wenn Fehler nicht normal sind, und andere Tests wie Wald-Test oder LR-Test verwendet werden sollten.

Restposten

Die gewöhnliche Analyse der kleinsten Quadrate umfasst häufig die Verwendung von diagnostischen Diagrammen, die entwickelt wurden, um Abweichungen der Daten von der angenommenen Form des Modells zu erkennen. Dies sind einige der häufigsten diagnostischen Diagramme:

• Residuen gegen die erklärenden Variablen im Modell. Eine nichtlineare Beziehung zwischen diesen Variablen deutet darauf hin, dass die Linearität der bedingten Mittelwertfunktion möglicherweise nicht gilt. Unterschiedliche Variabilitätsgrade in den Residuen für unterschiedliche Niveaus der erklärenden Variablen deuten auf eine mögliche Heteroskedastizität hin.
• Residuen gegen erklärende Variablen, die nicht im Modell enthalten sind. Jede Beziehung der Residuen zu diesen Variablen würde nahelegen, diese Variablen für die Einbeziehung in das Modell in Betracht zu ziehen.
• Residuen gegen die angepassten Werte, .${\displaystyle {\hat {y}}}$
• Residuen gegen das vorhergehende Residuum. Dieses Diagramm kann serielle Korrelationen in den Residuen identifizieren.

Eine wichtige Überlegung bei der Durchführung statistischer Inferenz unter Verwendung von Regressionsmodellen ist, wie die Daten erfasst wurden. In diesem Beispiel sind die Daten Durchschnittswerte und keine Messwerte für einzelne Frauen. Die Passform des Modells ist sehr gut, dies bedeutet jedoch nicht, dass das Gewicht einer einzelnen Frau nur anhand ihrer Körpergröße mit hoher Genauigkeit vorhergesagt werden kann.

Rundungsempfindlichkeit

Dieses Beispiel zeigt auch, dass die durch diese Berechnungen bestimmten Koeffizienten empfindlich darauf sind, wie die Daten aufbereitet werden. Die Höhen wurden ursprünglich auf den nächsten Zoll gerundet angegeben und wurden umgerechnet und auf den nächsten Zentimeter gerundet. Da der Umrechnungsfaktor ein Zoll auf 2,54 cm beträgt, ist dies keine genaue Umrechnung. Die ursprünglichen Zoll können durch Round(x/0.0254) wiederhergestellt und dann ohne Rundung wieder in metrische Werte umgewandelt werden. Wenn dies geschieht, werden die Ergebnisse:

Residuen einer quadratischen Anpassung für richtig und falsch konvertierte Daten.

Die Verwendung einer dieser Gleichungen zur Vorhersage des Gewichts einer 1,6764 m großen Frau ergibt ähnliche Werte: 62,94 kg mit Rundung vs. 62,98 kg ohne Rundung. Somit hat eine scheinbar kleine Abweichung in den Daten eine echte Auswirkung auf die Koeffizienten aber einen kleinen Effekt auf die Ergebnisse der Gleichung.

Während dies in der Mitte des Datenbereichs harmlos erscheinen mag, kann es an den Extremen oder in dem Fall, in dem das angepasste Modell verwendet wird, um außerhalb des Datenbereichs zu projizieren ( Extrapolation ) , signifikant werden .

Dies hebt einen häufigen Fehler hervor: Dieses Beispiel ist ein Missbrauch von OLS, der von Natur aus erfordert, dass die Fehler in der unabhängigen Variablen (in diesem Fall Höhe) null oder zumindest vernachlässigbar sind. Die anfängliche Rundung auf den nächsten Zoll plus alle tatsächlichen Messfehler stellen einen endlichen und nicht zu vernachlässigenden Fehler dar. Infolgedessen sind die angepassten Parameter nicht die besten Schätzungen, für die sie angenommen werden. Obwohl nicht völlig falsch, hängt der Fehler bei der Schätzung von der relativen Größe der x- und y- Fehler ab.

Ein weiteres Beispiel mit weniger echten Daten

Problemstellung

Wir können den Mechanismus der kleinsten Quadrate verwenden, um die Gleichung einer Zweikörperbahn in polaren Basiskoordinaten zu berechnen. Die normalerweise verwendete Gleichung lautet: Wo ist der Radius, wie weit das Objekt von einem der Körper entfernt ist. In der Gleichung werden die Parameter und verwendet, um den Bahnverlauf zu bestimmen. Wir haben die folgenden Daten gemessen. ${\displaystyle r(\theta)={\frac {p}{1-e\cos(\theta)}}}$${\displaystyle r(\theta)}$${\displaystyle p}$${\displaystyle e}$

${\displaystyle\theta}$ (in Grad)	43	45	52	93	108	116
${\displaystyle r(\theta)}$	4.7126	4.5542	4.0419	2.2187	1.8910	1,7599

Wir müssen die kleinste-Quadrate-Approximation von und für die gegebenen Daten finden. ${\displaystyle e}$${\displaystyle p}$

Lösung

Zuerst müssen wir e und p in einer linearen Form darstellen. Also werden wir die Gleichung umschreiben als . Jetzt können wir dieses Formular verwenden, um unsere Beobachtungsdaten wie folgt darzustellen: ${\displaystyle r(\theta)}$${\displaystyle {\frac{1}{r(\theta)}}={\frac{1}{p}}-{\frac{e}{p}}\cos(\theta)}$

${\displaystyle A^{T}A{\binom {x}{y}}=A^{T}b}$wobei ist und ist und wird konstruiert, indem die erste Spalte der Koeffizient von ist und die zweite Spalte der Koeffizient von ist und die Werte für die jeweiligen so und${\displaystyle x}$${\displaystyle {\frac {1}{p}}}$${\displaystyle y}$${\displaystyle {\frac {e}{p}}}$${\displaystyle A}$${\displaystyle {\frac {1}{p}}}$${\displaystyle {\frac {e}{p}}}$${\displaystyle b}$${\displaystyle {\frac {1}{r(\theta)}}}$${\displaystyle A={\begin{bmatrix}1&-0.731354\\1&-0.707107\\1&-0.615661\\1&\ 0.052336\\1&0.309017\\1&0.438371\end{bmatrix}}}$${\displaystyle b={\begin{bmatrix}0.21220\\0.21958\\0.24741\\0.45071\\0.52883\\0.56820\end{bmatrix}}.}$

Beim Lösen erhalten wir ${\displaystyle {\binom {x}{y}}={\binom {0.43478}{0.30435}}}$

also und${\displaystyle p={\frac {1}{x}}=2.3000}$${\displaystyle e=p\cdot y=0.70001}$

Siehe auch

• Bayessche kleinste Quadrate
• Fama-MacBeth-Regression
• Nichtlineare kleinste Quadrate
• Numerische Methoden für lineare kleinste Quadrate
• Nichtlineare Systemidentifikation

Verweise

Weiterlesen

• Dougherty, Christopher (2002). Einführung in die Ökonometrie (2. Aufl.). New York: Oxford University Press. S. 48–113. ISBN 0-19-877643-8.
• Gujarati, Damodar N. ; Porter, Dawn C. (2009). Grundlegende Ökonomie (Fünfte Aufl.). Boston: McGraw-Hill Irwin. S. 55–96. ISBN 978-0-07-337577-9.
• Heij, Christiaan; Bure, Paul; Franses, Philipp H.; Kloek, Teun; van Dijk, Herman K. (2004). Ökonometrische Methoden mit betriebswirtschaftlichen Anwendungen (1. Aufl.). Oxford: Oxford University Press. S. 76–115. ISBN 978-0-19-926801-6.
• Hill, R. Carter; Griffiths, William E.; Lim, Guay C. (2008). Prinzipien der Ökonometrie (3. Aufl.). Hoboken, New Jersey: John Wiley & Söhne. S. 8–47. ISBN 978-0-471-72360-8.
• Wooldridge, Jeffrey (2008). "Das einfache Regressionsmodell" . Einführende Ökonometrie: Ein moderner Ansatz (4. Aufl.). Mason, OH: Cengage-Lernen. S. 22–67. ISBN 978-0-324-58162-1.