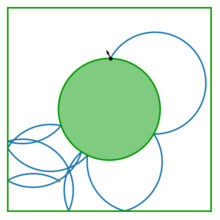
Dynamisches Billard - Dynamical billiards

Ein Teilchen, das sich im Bunimovich-Stadion bewegt, einem bekannten chaotischen Billard. Informationen zum Erstellen einer solchen Animation finden Sie im Abschnitt Software.

Ein dynamisches Billard ist ein dynamisches System, in dem ein Partikel zwischen freier Bewegung (typischerweise als gerade Linie) und spiegelnden Reflexionen von einer Grenze wechselt. Wenn die Teilchen die Grenze trifft reflektiert es von ihm ohne Verlust der Geschwindigkeit (dh elastische Stöße). Billard sind Hamiltonsche Idealisierungen des Billardspiels , wobei die von der Grenze eingeschlossene Region jedoch auch andere Formen als rechteckig und sogar mehrdimensional sein kann. Dynamisches Billard kann auch an nichteuklidischen Geometrien studiert werden ; Tatsächlich haben die ersten Billardstudien ihre ergodische Bewegung auf Oberflächen mit konstanter negativer Krümmung festgestellt . Das Studium von Billard, das nicht in einer Region, sondern außerhalb einer Region aufbewahrt wird, wird als äußere Billardtheorie bezeichnet .

Die Bewegung des Teilchens im Billard ist eine gerade Linie mit konstanter Energie zwischen Reflexionen an der Grenze (eine Geodäte, wenn die Riemannsche Metrik des Billardtisches nicht flach ist). Alle Reflexionen sind spiegelnd : Der Einfallswinkel kurz vor der Kollision ist gleich dem Reflexionswinkel kurz nach der Kollision. Die Abfolge der Reflexionen wird durch die Billardkarte beschrieben , die die Bewegung des Teilchens vollständig charakterisiert.

Billard erfasst die gesamte Komplexität von Hamilton-Systemen, von der Integrierbarkeit bis zur chaotischen Bewegung , ohne die Schwierigkeiten, die Bewegungsgleichungen zu integrieren , um ihre Poincaré-Karte zu bestimmen . Birkhoff zeigte, dass ein Billardsystem mit einem Ellipsentisch integrierbar ist.

Bewegungsgleichungen

Der Hamilton-Operator für ein Teilchen der Masse m, das sich frei ohne Reibung auf einer Oberfläche bewegt, lautet:

${\displaystyle H(p,q)={\frac {p^{2}}{2m}}+V(q)}$

wo ist ein Potential, das innerhalb des Bereichs, in dem sich das Teilchen bewegen kann, null ist, andernfalls unendlich: ${\displaystyle V(q)}$${\displaystyle \Omega}$

${\displaystyle V(q)={\begin{cases}0&q\in \Omega \\\infty &q\notin \Omega \end{cases}}}$

Diese Form des Potentials garantiert eine spiegelnde Reflexion an der Grenze. Der kinetische Term garantiert, dass sich das Teilchen geradlinig bewegt, ohne dass sich die Energie ändert. Wenn sich das Teilchen auf einer nichteuklidischen Mannigfaltigkeit bewegen soll , wird der Hamilton-Operator ersetzt durch:

${\displaystyle H(p,q)={\frac {1}{2m}}p^{i}p^{j}g_{ij}(q)+V(q)}$

wo ist der metrische Tensor im Punkt . Wegen der sehr einfachen Struktur dieses Hamilton-Operators sind die Bewegungsgleichungen für das Teilchen, die Hamilton-Jacobi-Gleichungen , nichts anderes als die geodätischen Gleichungen auf der Mannigfaltigkeit: Das Teilchen bewegt sich entlang von Geodäten . ${\displaystyle g_{ij}(q)}$${\displaystyle q\;\in\;\Omega}$

Bemerkenswerte Billard- und Billardkurse

Hadamards Billard

Bei Hadamards Billard handelt es sich um die Bewegung eines freien Punktteilchens auf einer Fläche konstanter negativer Krümmung, insbesondere der einfachsten kompakten Riemann-Fläche mit negativer Krümmung, einer Fläche der Gattung 2 (ein Zweiloch-Donut). Das Modell ist exakt lösbar und wird durch die geodätische Strömung an der Oberfläche gegeben. Es ist das früheste Beispiel für deterministisches Chaos, das jemals untersucht wurde und wurde 1898 von Jacques Hadamard eingeführt .

Artins Billard

Artins Billard betrachtet die freie Bewegung eines Punktteilchens auf einer Fläche konstanter negativer Krümmung, insbesondere der einfachsten nicht kompakten Riemannschen Fläche , einer Fläche mit einer Spitze. Es zeichnet sich dadurch aus, dass es exakt lösbar ist und dennoch nicht nur ergodisch, sondern auch stark mischend ist . Es ist ein Beispiel für ein Anosov-System . Dieses System wurde erstmals 1924 von Emil Artin untersucht .

Dispergierendes und semi-dispergierendes Billard

Sei M eine vollständige glatte Riemannsche Mannigfaltigkeit ohne Rand, deren maximale Schnittkrümmung nicht größer als K ist und mit dem Injektivitätsradius . Betrachten Sie eine Sammlung von n geodätisch konvexen Teilmengen (Wände) , , so dass ihre Grenzen glatte Untermannigfaltigkeiten der Kodimension eins sind. Sei , wobei bezeichnet das Innere der Menge . Das Set wird Billardtisch genannt. Betrachten wir nun ein Teilchen, das sich innerhalb der Menge B mit Einheitsgeschwindigkeit entlang einer Geodäte bewegt, bis es eine der Mengen B _{i erreicht} (ein solches Ereignis wird Kollision genannt), wo es nach dem Gesetz „Der Einfallswinkel ist gleich dem Reflexionswinkel“ (wenn er eine der Mengen erreicht , , ist die Flugbahn nach diesem Moment nicht definiert). Ein solches dynamisches System wird als semi-dispergierendes Billard bezeichnet . Wenn die Wände streng konvex sind, wird das Billard als Dispergieren bezeichnet . Die Benennung wird durch die Beobachtung motiviert, dass sich ein lokal paralleler Strahl von Trajektorien nach einer Kollision mit einem streng konvexen Teil einer Wand zerstreut, aber nach einer Kollision mit einem flachen Abschnitt einer Wand lokal parallel bleibt. ${\displaystyle \rho >0}$${\displaystyle B_{i}\subset M}$${\displaystyle i=1,\ldots,n}$${\displaystyle B=M\ (\bigcup_{i=1}^{n}\operatorname {Int} (B_{i}))}$${\displaystyle \operatorname {Int} (B_{i})}$${\displaystyle B_{i}}$${\displaystyle B\subset M}$${\displaystyle B_{i}\cap B_{j}}$${\displaystyle i\neq j}$

Die dispergierende Grenze spielt beim Billard die gleiche Rolle wie die negative Krümmung bei geodätischen Strömungen, was die exponentielle Instabilität der Dynamik verursacht. Es ist genau dieser Dispergiermechanismus, der dem Dispergieren von Billard seine stärksten chaotischen Eigenschaften verleiht, wie er von Yakov G. Sinai festgestellt wurde . Das Billard ist nämlich ergodisch , mischt , Bernoulli , hat eine positive Kolmogorov-Sinai- Entropie und einen exponentiellen Abfall der Korrelationen .

Chaotische Eigenschaften des allgemeinen halb-Dispersions Billards nicht verstanden werden, dass gut, aber die von einer wichtigen Art von halb-Dispersions Billard, Gas harte Kugel untersucht wurde , in einigen Details seit 1975 (siehe nächsten Abschnitt).

Allgemeine Ergebnisse von Dmitri Burago und Serge Ferleger zur einheitlichen Schätzung der Kollisionszahl in nicht entarteten semi-dispersiven Billards erlauben die Endlichkeit seiner topologischen Entropie und nicht mehr als ein exponentielles Wachstum periodischer Trajektorien. Im Gegensatz dazu können degenerierte, halbdisperse Billardtische eine unendliche topologische Entropie aufweisen.

Lorentz-Gas, auch bekannt als Sinai-Billard

Ein Teilchen, das sich im Sinai-Billard bewegt, auch als Lorentz-Gas bekannt.

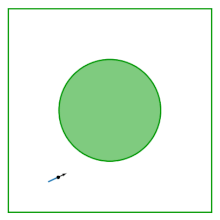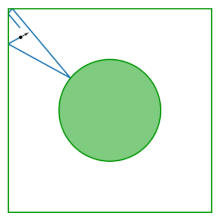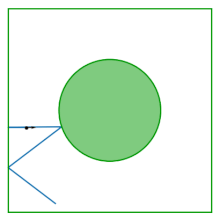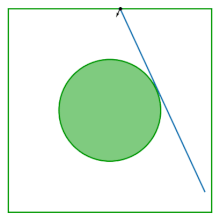
Der Tisch des Lorentz-Gases (auch als Sinai-Billard bekannt) ist ein Quadrat, in dessen Mitte eine Scheibe entfernt ist; der Tisch ist flach und hat keine Krümmung. Das Billard entsteht aus der Untersuchung des Verhaltens zweier interagierender Scheiben, die innerhalb eines Quadrats hüpfen und von den Grenzen des Quadrats und voneinander reflektiert werden. Durch den Wegfall des Massenschwerpunktes als Konfigurationsvariable reduziert sich die Dynamik zweier interagierender Scheiben auf die Dynamik im Sinai-Billard.

Das Billard wurde von Yakov G. Sinai als Beispiel für ein wechselwirkendes Hamilton-System eingeführt , das physikalische thermodynamische Eigenschaften aufweist: Fast alle (bis zu einem Maß Null) seiner möglichen Flugbahnen sind ergodisch und es hat einen positiven Lyapunov-Exponenten .

Die große Leistung des Sinai mit diesem Modell bestand darin, zu zeigen, dass das klassische Boltzmann-Gibbs-Ensemble für ein ideales Gas im Wesentlichen das maximal chaotische Hadamard-Billard ist.

Bunimovich-Stadion

Der Tisch namens Bunimovich-Stadion ist ein Rechteck, das von Halbkreisen bedeckt ist, eine Form, die Stadion genannt wird . Bis zu seiner Einführung durch Leonid Bunimovich dachte man, dass Billard mit positiven Lyapunov-Exponenten konvexe Streuungen benötigen, wie die Scheibe im Sinai-Billard, um die exponentielle Divergenz der Bahnen zu erzeugen. Bunimovich zeigte, dass durch die Betrachtung der Bahnen jenseits des Brennpunkts einer konkaven Region eine exponentielle Divergenz erhalten werden kann.

Magnetbillard

Bewegung eines geladenen Teilchens in einem Sinai-Billard mit senkrechtem Magnetfeld.

Magnetisches Billard stellt Billard dar, bei dem sich ein geladenes Teilchen unter einem senkrechten Magnetfeld ausbreitet. Dadurch ändert sich die Partikelflugbahn von einer Geraden in einen Kreisbogen. Der Radius dieses Kreises ist umgekehrt proportional zur magnetischen Feldstärke. Solche Billards haben sich in realen Billardanwendungen als nützlich erwiesen , typischerweise bei der Modellierung von Nanovorrichtungen (siehe Anwendungen).

Generalisiertes Billard

Generalisiertes Billard (GB) beschreibt eine Bewegung eines Massenpunktes (ein Teilchen) innerhalb einer geschlossenen Domäne mit der stückweise glatten Grenze . An der Grenze wird die Punktgeschwindigkeit transformiert, wenn das Teilchen der Wirkung des verallgemeinerten Billardgesetzes unterliegt. GB wurden von Lev D. Pustyl'nikov im allgemeinen Fall eingeführt, und im Falle eines Parallelepipeds im Zusammenhang mit der Begründung des zweiten Hauptsatzes der Thermodynamik . Physikalisch betrachtet beschreibt GB ein Gas, das aus endlich vielen Teilchen besteht, die sich in einem Gefäß bewegen, während sich die Gefäßwände aufheizen oder abkühlen. Das Wesen der Verallgemeinerung ist das Folgende. Wenn das Teilchen auf die Grenze trifft , transformiert sich seine Geschwindigkeit mit Hilfe einer gegebenen Funktion , die auf dem direkten Produkt (wo ist die reelle Linie, ist ein Punkt der Grenze und ist die Zeit) definiert ist, gemäß dem folgenden Gesetz. Nehmen wir an, dass die Flugbahn des Teilchens, das mit der Geschwindigkeit bewegt , schneidet sich am Punkt zum Zeitpunkt . Dann nimmt das Teilchen mit der Zeit die Geschwindigkeit an , als ob es einen elastischen Schub von der unendlich schweren Ebene erfahren würde , die den Punkt tangential ist , und bewegt sich dann mit der Geschwindigkeit entlang der Normalen zu at . Wir betonen, dass die Lage des Randes selbst festgelegt ist, während seine Wirkung auf das Teilchen durch die Funktion definiert wird . ${\displaystyle \Pi\,\subset\,\mathbb{R}^{n}}$${\displaystyle \Gamma}$${\displaystyle \Gamma}$${\displaystyle\Pi}$${\displaystyle \Gamma}$${\displaystyle f(\gamma,\,t)}$${\displaystyle \Gamma\,\times\,\mathbb{R}^{1}}$${\displaystyle \mathbb {R} ^{1}}$${\displaystyle \gamma\,\in\,\Gamma}$${\displaystyle t\,\in\,\mathbb {R} ^{1}}$${\displaystyle v}$${\displaystyle \Gamma}$${\displaystyle \gamma\,\in\,\Gamma}$${\displaystyle t^{*}}$${\displaystyle t^{*}}$${\displaystyle v^{*}}$${\displaystyle \Gamma^{*}}$${\displaystyle \Gamma}$${\displaystyle\gamma}$${\displaystyle t^{*}}$${\displaystyle \Gamma}$${\displaystyle\gamma}$${\displaystyle \textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t^{*})}$${\displaystyle f}$

Die positive Bewegungsrichtung der Ebene nehmen wir zum Inneren von hin . Wenn also die Ableitung , dann beschleunigt das Teilchen nach dem Aufprall. ${\displaystyle \Gamma^{*}}$${\displaystyle\Pi}$${\displaystyle \textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t)\;>\;0}$

Wenn die Geschwindigkeit , die das Teilchen als Ergebnis des obigen Reflexionsgesetzes erhält, auf das Innere der Domäne gerichtet ist , dann verlässt das Teilchen die Grenze und bewegt sich bis zur nächsten Kollision mit weiter hinein . Wenn die Geschwindigkeit nach außen gerichtet ist , bleibt das Teilchen an dem Punkt, bis irgendwann die Wechselwirkung mit der Grenze das Teilchen dazu zwingt, es zu verlassen. ${\displaystyle v^{*}}$${\displaystyle\Pi}$${\displaystyle\Pi}$${\displaystyle \Gamma}$${\displaystyle v^{*}}$${\displaystyle\Pi}$${\displaystyle \Gamma}$${\displaystyle\gamma}$${\displaystyle {\tilde{t}}\;>\;t^{*}}$

Wenn die Funktion nicht zeitabhängig ist ; dh das verallgemeinerte Billard fällt mit dem klassischen zusammen. ${\displaystyle f(\gamma,\,t)}$${\displaystyle t}$${\displaystyle \textstyle {\frac {\partial f}{\partial t}}\;=\;0}$

Dieses verallgemeinerte Reflexionsgesetz ist sehr natürlich. Erstens spiegelt es eine offensichtliche Tatsache wider, dass die Wände des Gefäßes mit Gas bewegungslos sind. Zweitens ist die Wirkung der Wand auf das Teilchen immer noch der klassische elastische Schub. Im Wesentlichen betrachten wir infinitesimal bewegte Grenzen mit gegebenen Geschwindigkeiten.

Sie gilt sowohl im Rahmen der klassischen Mechanik (Newtonscher Fall) als auch der Relativitätstheorie (relativistischer Fall) als Reflexion vom Rand . ${\displaystyle \Gamma}$

Hauptergebnisse: Im Newtonschen Fall ist die Energie des Teilchens beschränkt, die Gibbs-Entropie ist eine Konstante, (in Anmerkungen) und im relativistischen Fall wächst die Energie des Teilchens, die Gibbs-Entropie, die Entropie in Bezug auf das Phasenvolumen ins Unendliche, (in Anmerkungen), Verweise auf verallgemeinertes Billard.

Quantenchaos

Die Quantenversion des Billards wird auf verschiedene Weise leicht untersucht. Der oben angegebene klassische Hamilton-Operator für das Billard wird durch die stationäre Schrödinger-Gleichung oder genauer gesagt durch ${\displaystyle H\psi\;=\;E\psi}$

${\displaystyle -{\frac {\hbar^{2}}{2m}}\nabla^{2}\psi_{n}(q)=E_{n}\psi_{n}(q)}$

wo ist der Laplace . Das Potenzial, das außerhalb der Region unendlich ist, aber darin null ist, übersetzt sich in die Dirichlet-Randbedingungen : ${\displaystyle \nabla ^{2}}$${\displaystyle \Omega}$

${\displaystyle \psi_{n}(q)=0\quad {\mbox{für}}\quad q\notin \Omega}$

Wie üblich werden die Wellenfunktionen als orthonormal angenommen :

${\displaystyle \int_{\Omega}{\overline {\psi_{m}}}(q)\psi_{n}(q)\,dq=\delta_{mn}}$

Seltsamerweise ist die Freifeld-Schrödinger-Gleichung dieselbe wie die Helmholtz-Gleichung .

${\displaystyle \left(\nabla^{2}+k^{2}\right)\psi =0}$

mit

${\displaystyle k^{2}={\frac {1}{\hbar^{2}}}2mE_{n}}$

Dies impliziert, dass zwei- und dreidimensionale Quantenbillards durch die klassischen Resonanzmoden eines Radarhohlraums einer bestimmten Form modelliert werden können , wodurch eine Tür zur experimentellen Verifikation geöffnet wird. (Die Untersuchung von Radarhohlraummoden muss auf die transversalen magnetischen (TM) Moden beschränkt werden, da diese die Dirichlet-Randbedingungen erfüllen).

Die semiklassische Grenze entspricht der, die als äquivalent zu angesehen werden kann , wobei die Masse zunimmt, so dass sie sich klassisch verhält. ${\displaystyle \hbar\;\to\;0}$${\displaystyle m\;\to \;\infty}$

Als allgemeine Aussage kann man sagen, dass immer dann, wenn die klassischen Bewegungsgleichungen integrierbar sind (zB rechteckige oder runde Billardtische), die quantenmechanische Version des Billards vollständig lösbar ist. Wenn das klassische System chaotisch ist, dann ist das Quantensystem im Allgemeinen nicht genau lösbar und weist zahlreiche Schwierigkeiten bei seiner Quantisierung und Auswertung auf. Das allgemeine Studium chaotischer Quantensysteme wird als Quantenchaos bezeichnet .

Ein besonders auffälliges Beispiel für Narbenbildung auf einem elliptischen Tisch ist die Beobachtung der sogenannten Quanten-Trugbilder .

Anwendungen

Billard, sowohl Quanten- als auch klassisches Billard, wurde in mehreren Bereichen der Physik angewendet, um ganz unterschiedliche reale Systeme zu modellieren. Beispiele umfassen Strahlenoptik , Laser , Akustik , optische Fasern (z. B. Doppelmantelfasern ) oder quantenklassische Korrespondenz. Eine ihrer häufigsten Anwendungen ist die Modellierung von Partikeln, die sich innerhalb von Nanogeräten bewegen, zum Beispiel Quantenpunkte , pn-Übergänge , Antidot-Übergitter und andere. Der Grund für diese weit verbreitete Wirksamkeit des Billards als physikalisches Modell liegt darin, dass in Situationen mit geringer Unordnung oder Rauschen die Bewegung von z. B. Teilchen wie Elektronen oder Lichtstrahlen der Bewegung des Punkts sehr ähnlich ist. Partikel im Billard. Darüber hinaus spiegelt die energieerhaltende Natur der Teilchenkollisionen direkt die Energieerhaltung der Hamiltonschen Mechanik wider.

Software

Open-Source-Software zur Simulation von Billard gibt es für verschiedene Programmiersprachen. Von der neuesten bis zur ältesten existierenden Software: DynamicalBilliards.jl (Julia), Bill2D (C++) und Billiard Simulator (Matlab). Die Animationen auf dieser Seite wurden mit DynamicalBilliards.jl erstellt.

Siehe auch

• Fermi-Ulam-Modell (Billard mit schwingenden Wänden)
• Der Lubachevsky-Stillinger-Algorithmus der Kompression simuliert harte Kugeln , die nicht nur mit den Grenzen, sondern auch untereinander kollidieren, während sie in der Größe wachsen
• Arithmetisches Billard

Anmerkungen

Verweise

Billard auf dem Sinai

• Sinai, Ja. G. (1963). „[Auf den Grundlagen der ergodischen Hypothese für ein dynamisches System der statistischen Mechanik]“. Doklady Akademii Nauk SSSR (auf Russisch). 153 (6): 1261-1264.(in Englisch, Sov. Math Dokl. 4 (1963) S. 1818–1822).
• Ja. G. Sinai, "Dynamische Systeme mit elastischen Reflexionen", Russian Mathematical Surveys , 25 , (1970) S. 137–191.
• VI Arnold und A. Avez, Théorie ergodique des systèms dynamiques , (1967), Gauthier-Villars, Paris. (Englische Ausgabe: Benjamin-Cummings, Reading, Mass. 1968). (Bietet Diskussion und Referenzen für Sinai's Billard.)
• D. Heitmann, JP Kotthaus, "The Spectroscopy of Quantum Dot Arrays", Physics Today (1993) S. 56–63. (Gibt einen Überblick über experimentelle Tests von Quantenversionen von Sinai-Billards, die als nanoskalige (mesoskopische) Strukturen auf Siliziumwafern realisiert wurden.)
• S. Sridhar und WT Lu, „ Sinai Billiards, Ruelle Zeta-functions and Ruelle Resonances: Microwave Experiments “, (2002) Journal of Statistical Physics , Vol. 2, No. 108 Nr. 5/6, S. 755–766.
• Linas Vepstas, Sinais Billard , (2001). (Bietet Raytracing-Bilder von Sinais Billard im dreidimensionalen Raum. Diese Bilder bieten eine grafische, intuitive Demonstration der starken Ergodizität des Systems.)
• N. Chernov und R. Markarian, "Chaotic Billiards", 2006, Mathematische Übersicht und Monographien Nr. 127, AMS.

Seltsames Billard

• T. Schürmann und I. Hoffmann, Die Entropie des seltsamen Billards in n-Simplexen. J.Phys. A28, Seite 5033ff, 1995. PDF-Dokument

Bunimovich-Stadion

• LABunimovich (1979). „Über die ergodischen Eigenschaften von nirgendwo zerstreuendem Billard“. Commun Math Phys . 65 (3): 295–312. Bibcode : 1979CMaPh..65..295B . doi : 10.1007/BF01197884 .
• LABunimovich & Ya. G. Sinai (1980). „Markov-Partitionen für verteiltes Billard“. Commun Math Phys . 78 (2): 247–280. Bibcode : 1980CMaPh..78..247B . doi : 10.1007/bf01942372 .
• Flash-Animation zum chaotischen Bunimovich-Stadion

Generalisiertes Billard

• MV Deryabin und LD Pustyl'nikov, "Generalisiertes relativistisches Billard", Reg. und Chaotischer Dyn. 8(3), S. 283–296 (2003).
• MV Deryabin und LD Pustyl'nikov, "On Generalized Relativistic Billiards in External Force Fields", Letters in Mathematical Physics , 63(3), S. 195–207 (2003).
• MV Deryabin und LD Pustyl'nikov, "Exponentielle Attraktoren in generalisiertem relativistischem Billard", Comm. Mathematik. Phys. 248(3), S. 527–552 (2004).

Externe Links

• Weisstein, Eric W. "Billard" . MathWorld .
• Scholarpedia-Eintrag zu Dynamischem Billard (Leonid Bunimovich)
• Einführung in dynamische Systeme mit Billard , Max-Planck-Institut für Physik komplexer Systeme