Elektronische Bandstruktur - Electronic band structure

In der Festkörperphysik beschreibt die elektronische Bandstruktur (oder einfach Bandstruktur ) eines Festkörpers den Bereich der Energieniveaus , die Elektronen in ihm haben können, sowie die Energiebereiche, die sie möglicherweise nicht haben (sogenannte Bandlücken oder verbotene). Bänder ).

Die Bandtheorie leitet diese Bänder und Bandlücken ab, indem sie die zulässigen quantenmechanischen Wellenfunktionen für ein Elektron in einem großen, periodischen Gitter von Atomen oder Molekülen untersucht. Die Bandtheorie wurde erfolgreich verwendet, um viele physikalische Eigenschaften von Festkörpern wie den spezifischen elektrischen Widerstand und die optische Absorption zu erklären , und bildet die Grundlage für das Verständnis aller Festkörperbauelemente (Transistoren, Solarzellen usw.).

Warum Bands und Bandlücken auftreten

Ein hypothetisches Beispiel für die Zusammenführung einer großen Anzahl von Kohlenstoffatomen zu einem Diamantkristall, was die Bildung der elektronischen Bandstruktur demonstriert. Die rechte Grafik zeigt die Energieniveaus als Funktion der Kristallzellgröße (ein typischer Atomabstand). Wenn sie weit voneinander entfernt sind, haben alle N- Atome diskrete Valenzorbitale p und s . Wenn sich die Atome jedoch nähern, beginnen sich ihre Elektronenorbitale räumlich zu überlappen und aufgrund des Pauli-Ausschlussprinzips teilt sich jedes Atomniveau in N Niveaus mit unterschiedlichen Energien auf. Da N eine sehr große Zahl ist, liegen die benachbarten Niveaus energetisch nahe beieinander und bilden effektiv ein kontinuierliches Energieband. Bei der tatsächlichen Diamantkristallzellengröße (bezeichnet durch a ) werden zwei Bänder gebildet, die Valenz- und Leitungsbänder genannt werden, die durch eine 5,5-eV-Bandlücke getrennt sind. Ein weiteres Verringern des Atomabstands (z. B. unter hohem Druck) modifiziert die Bandstruktur weiter.

Medien abspielen

Animation der Bandbildung und wie Elektronen sie in einem Metall und einem Isolator füllen

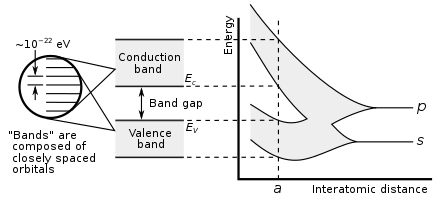
Die Elektronen eines einzelnen, isolierten Atoms besetzen Atomorbitale, von denen jedes ein diskretes Energieniveau hat . Wenn sich zwei oder mehr Atome zu einem Molekül verbinden , überlappen sich ihre Atomorbitale. Das Pauli-Ausschlussprinzip besagt, dass in einem Molekül keine zwei Elektronen die gleichen Quantenzahlen haben können. Wenn sich also zwei identische Atome zu einem zweiatomigen Molekül verbinden , teilt sich jedes Atomorbital in zwei Molekülorbitale unterschiedlicher Energie, sodass die Elektronen in den früheren Atomorbitalen die neue Orbitalstruktur besetzen können, ohne dass eines die gleiche Energie hat.

In ähnlicher Weise überlappen sich die Atomorbitale der Atome, wenn eine große Anzahl N identischer Atome zu einem Festkörper wie einem Kristallgitter zusammenkommen . Da das Pauli-Ausschlussprinzip vorschreibt, dass keine zwei Elektronen im Festkörper die gleichen Quantenzahlen haben, zerfällt jedes Atomorbital in N diskrete Molekülorbitale mit jeweils unterschiedlicher Energie. Da die Anzahl der Atome in einem makroskopischen Festkörperstück eine sehr große Zahl ist (N~10 ²² ), ist die Anzahl der Orbitale sehr groß und daher sind sie energetisch sehr nahe beieinander (in der Größenordnung von 10 ⁻²²  eV). Die Energie benachbarter Ebenen liegt so nah beieinander, dass man sie als Kontinuum, ein Energieband, betrachten kann.

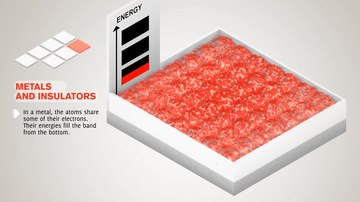
Diese Bandenbildung ist meist ein Merkmal der äußersten Elektronen ( Valenzelektronen ) im Atom, die an der chemischen Bindung und der elektrischen Leitfähigkeit beteiligt sind . Die inneren Elektronenorbitale überlappen sich nicht nennenswert, daher sind ihre Bänder sehr schmal.

Bandlücken sind im Wesentlichen übrig gebliebene Energiebereiche, die von keinem Band abgedeckt werden, als Ergebnis der endlichen Breiten der Energiebänder. Die Bänder haben unterschiedliche Breiten, wobei die Breiten vom Grad der Überlappung in den Atomorbitalen, aus denen sie stammen, abhängen. Zwei benachbarte Bänder können einfach nicht breit genug sein, um den Energiebereich vollständig abzudecken. Zum Beispiel sind die mit Kernorbitalen assoziierten Bänder (wie 1s-Elektronen ) aufgrund der kleinen Überlappung zwischen benachbarten Atomen extrem schmal. Als Ergebnis besteht die Tendenz, dass es große Bandlücken zwischen den Kernbändern gibt. Höhere Bänder umfassen vergleichsweise größere Orbitale mit mehr Überlappung, die bei höheren Energien zunehmend breiter werden, so dass bei höheren Energien keine Bandlücken auftreten.

Grundlegendes Konzept

Annahmen und Grenzen der Bandstrukturtheorie

Die Bandtheorie ist nur eine Annäherung an den Quantenzustand eines Festkörpers, die für Festkörper gilt, die aus vielen identischen Atomen oder miteinander verbundenen Molekülen bestehen. Dies sind die Annahmen, die für die Gültigkeit der Bandtheorie erforderlich sind:

• System unendlicher Größe : Damit die Bänder kontinuierlich sind, muss das Materialstück aus einer großen Anzahl von Atomen bestehen. Da ein makroskopisches Materialstück etwa 10 ²² Atome enthält, ist dies keine ernsthafte Einschränkung; Die Bandtheorie gilt sogar für mikroskopisch kleine Transistoren in integrierten Schaltkreisen . Mit Modifikationen kann das Konzept der Bandstruktur auch auf Systeme ausgedehnt werden, die nur entlang einiger Dimensionen "groß" sind, wie beispielsweise zweidimensionale Elektronensysteme .
• Homogenes System : Die Bandstruktur ist eine intrinsische Eigenschaft eines Materials, die davon ausgeht, dass das Material homogen ist. In der Praxis bedeutet dies, dass die chemische Zusammensetzung des Materials im gesamten Teil einheitlich sein muss.
• Nichtinteraktivität : Die Bandstruktur beschreibt "Einzelelektronenzustände". Die Existenz dieser Zustände setzt voraus, dass sich die Elektronen in einem statischen Potential bewegen, ohne dynamisch mit Gitterschwingungen , anderen Elektronen, Photonen usw.

Die obigen Annahmen werden in einer Reihe wichtiger praktischer Situationen gebrochen, und die Verwendung der Bandstruktur erfordert eine genaue Überprüfung der Grenzen der Bandtheorie:

• Inhomogenitäten und Grenzflächen: In der Nähe von Oberflächen, Übergängen und anderen Inhomogenitäten wird die Volumenbandstruktur gestört. Es gibt nicht nur lokale kleinräumige Störungen (zB Oberflächenzustände oder Dotierstoffzustände innerhalb der Bandlücke), sondern auch lokale Ladungsungleichgewichte. Diese Ladungsungleichgewichte haben elektrostatische Effekte, die tief in Halbleiter, Isolatoren und das Vakuum hineinreichen (siehe Dotierung , Bandverbiegung ).
• In gleicher Weise betreffen die meisten elektronischen Effekte ( Kapazität , elektrische Leitfähigkeit , Abschirmung des elektrischen Felds ) die Physik von Elektronen, die durch Oberflächen und/oder in der Nähe von Grenzflächen passieren. Die vollständige Beschreibung dieser Effekte in einem Bandstrukturbild erfordert zumindest ein rudimentäres Modell der Elektron-Elektron-Wechselwirkungen (siehe Raumladung , Bandverbiegung ).
• Kleine Systeme: Für Systeme, die entlang jeder Dimension klein sind (zB ein kleines Molekül oder ein Quantenpunkt ), gibt es keine kontinuierliche Bandstruktur. Der Übergang zwischen kleinen und großen Dimensionen ist das Reich der mesoskopischen Physik .
• Stark korrelierte Materialien (z. B. Mott-Isolatoren ) können einfach nicht in Bezug auf Einzelelektronenzustände verstanden werden. Die elektronischen Bandstrukturen dieser Materialien sind schlecht definiert (oder zumindest nicht eindeutig definiert) und liefern möglicherweise keine nützlichen Informationen über ihren physikalischen Zustand.

Kristalline Symmetrie und Wellenvektoren

Abb. 1. Brillouin-Zone eines kubisch-flächenzentrierten Gitters mit Beschriftungen für spezielle Symmetriepunkte.

Abb. 2. Bandstrukturdiagramm für Si , Ge , GaAs und InAs, erzeugt mit einem engen Bindungsmodell. Beachten Sie, dass Si und Ge Materialien mit indirekter Bandlücke sind, während GaAs und InAs direkt sind.

Bandstrukturberechnungen nutzen die periodische Natur eines Kristallgitters und nutzen seine Symmetrie. Die Einelektronen- Schrödinger-Gleichung wird nach einem Elektron in einem gitterperiodischen Potential gelöst, was Bloch-Elektronen als Lösungen liefert:

${\displaystyle \psi_{n\mathbf{k}}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}u_{n\mathbf{k}}(\ mathbf {r} )}$,

wobei k als Wellenvektor bezeichnet wird. Für jeden Wert von k gibt es mehrere Lösungen der Schrödinger-Gleichung, gekennzeichnet mit n , dem Bandindex, der einfach die Energiebänder nummeriert. Jedes dieser Energieniveaus entwickelt sich glatt mit Änderungen von k und bildet ein glattes Zustandsband. Für jedes Band können wir eine Funktion E _n ( k ) definieren, die die Dispersionsrelation für Elektronen in diesem Band ist.

Der Wellenvektor nimmt jeden Wert innerhalb der Brillouin-Zone an , die ein Polyeder im Wellenvektorraum ( reziprokes Gitter ) ist, das sich auf das Kristallgitter bezieht. Wellenvektoren außerhalb der Brillouin-Zone entsprechen einfach Zuständen, die physikalisch mit den Zuständen innerhalb der Brillouin-Zone identisch sind. Besonderen Punkten/Linien mit hoher Symmetrie in der Brillouin-Zone werden Bezeichnungen wie Γ, Δ, Λ, Σ zugewiesen (siehe Abb. 1).

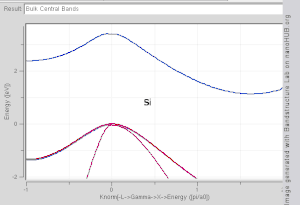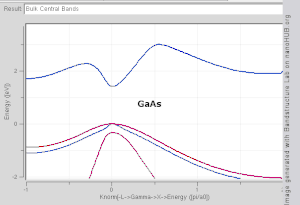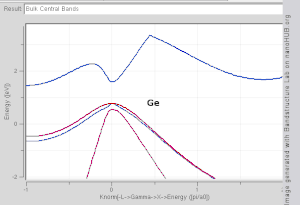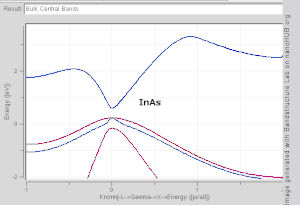
Es ist schwierig, sich die Form eines Bandes als Funktion des Wellenvektors vorzustellen, da dies eine Darstellung im vierdimensionalen Raum erfordern würde, E vs. k _x , k _y , k _z . In der wissenschaftlichen Literatur ist es üblich, Bandstrukturdiagramme zu sehen , die die Werte von E _n ( k ) für Werte von k entlang gerader Linien zeigen, die Symmetriepunkte verbinden, oft als Δ, Λ, Σ oder [100], [111] und . bezeichnet [110] bzw. Eine andere Methode zur Visualisierung der Bandstruktur besteht darin, eine Isofläche mit konstanter Energie im Wellenvektorraum darzustellen , die alle Zustände mit einer Energie gleich einem bestimmten Wert zeigt. Die Isofläche von Zuständen mit einer Energie gleich dem Fermi-Niveau wird als Fermi-Oberfläche bezeichnet .

Energiebandlücken können anhand der Wellenvektoren der die Bandlücke umgebenden Zustände klassifiziert werden:

• Direkte Bandlücke : Der Zustand mit der niedrigsten Energie oberhalb der Bandlücke hat das gleiche k wie der Zustand mit der höchsten Energie unterhalb der Bandlücke.
• Indirekte Bandlücke : Die nächsten Zustände oberhalb und unterhalb der Bandlücke haben nicht den gleichen k- Wert.

Asymmetrie: Bandstrukturen in nichtkristallinen Festkörpern

Obwohl elektronische Bandstrukturen normalerweise mit kristallinen Materialien assoziiert werden, können auch quasikristalline und amorphe Festkörper Bandlücken aufweisen. Diese sind theoretisch etwas schwieriger zu untersuchen, da ihnen die einfache Symmetrie eines Kristalls fehlt und es in der Regel nicht möglich ist, ein genaues Dispersionsverhältnis zu bestimmen. Infolgedessen konzentrierten sich praktisch alle existierenden theoretischen Arbeiten zur elektronischen Bandstruktur von Festkörpern auf kristalline Materialien.

Dichte der Staaten

Die Zustandsdichtefunktion g ( E ) ist definiert als die Anzahl der elektronischen Zustände pro Volumeneinheit pro Energieeinheit für Elektronenenergien in der Nähe von E .

Die Zustandsdichtefunktion ist wichtig für Effektberechnungen basierend auf der Bandtheorie. In Fermis Goldener Regel , einer Berechnung für die optische Absorptionsrate , liefert sie sowohl die Anzahl der anregbaren Elektronen als auch die Anzahl der Endzustände eines Elektrons. Es erscheint bei Berechnungen der elektrischen Leitfähigkeit, wo es die Anzahl der beweglichen Zustände liefert, und bei der Berechnung der Elektronenstreuraten, wo es die Anzahl der Endzustände nach der Streuung liefert.

Für Energien innerhalb einer Bandlücke ist g ( E ) = 0.

Füllen von Bändern

Füllung der elektronischen Zustände in verschiedenen Materialien im Gleichgewicht . Hier ist die Höhe die Energie, während die Breite die Dichte der verfügbaren Zustände für eine bestimmte Energie im aufgeführten Material ist. Die Schattierung folgt der Fermi-Dirac-Verteilung ( schwarz : alle Zustände gefüllt, weiß : kein Zustand gefüllt). In Metallen und Halbmetallen liegt das Fermi-Niveau E _F in mindestens einem Band.

In Isolatoren und Halbleitern liegt das Fermi-Niveau innerhalb einer Bandlücke ; In Halbleitern liegen die Bänder jedoch nahe genug am Fermi-Niveau, um thermisch mit Elektronen oder Löchern besetzt zu werden .

bearbeiten

Im thermodynamischen Gleichgewicht ist die Wahrscheinlichkeit, dass ein Energiezustand E mit einem Elektron gefüllt ist, durch die Fermi-Dirac-Verteilung gegeben , eine thermodynamische Verteilung, die das Pauli-Ausschlussprinzip berücksichtigt :

${\displaystyle f(E)={\frac {1}{1+e^{{(E-\mu)}/{k_{\rm {B}}T}}}}}$

wo:

• k _B T das Produkt aus Boltzmann-Konstante und Temperatur ist und
• µ ist das chemische Gesamtpotential der Elektronen oder das Fermi-Niveau (in der Halbleiterphysik wird diese Größe häufiger als E _{F bezeichnet} ). Der Fermi-Wert eines Festkörpers hängt direkt mit der Spannung an diesem Festkörper zusammen, die mit einem Voltmeter gemessen wird. Herkömmlicherweise wird in Bandstrukturdiagrammen das Fermi-Niveau als Nullpunkt der Energie angenommen (eine willkürliche Wahl).

Die Elektronendichte im Material ist einfach das Integral der Fermi-Dirac-Verteilung mal der Zustandsdichte:

${\displaystyle N/V=\int_{-\infty}^{\infty}g(E)f(E)\,dE}$

Obwohl es unendlich viele Bänder und damit unendlich viele Zustände gibt, gibt es in diesen Bändern nur eine endliche Anzahl von Elektronen. Der bevorzugte Wert für die Anzahl der Elektronen ist eine Folge der Elektrostatik: Obwohl die Oberfläche eines Materials aufgeladen werden kann, ist das innere Volumen eines Materials bevorzugt ladungsneutral. Die Bedingung der Ladungsneutralität bedeutet, dass N / V der Dichte der Protonen im Material entsprechen muss. Dazu passt sich das Material elektrostatisch an, indem es seine Bandstruktur energetisch nach oben oder unten verschiebt (wodurch g ( E ) verschoben wird ), bis es sich im richtigen Gleichgewicht in Bezug auf das Fermi-Niveau befindet.

Namen von Bändern in der Nähe des Fermi-Niveaus (Leitungsband, Valenzband)

Ein Festkörper hat unendlich viele erlaubte Bänder, genau wie ein Atom unendlich viele Energieniveaus hat. Die meisten Bänder haben jedoch einfach eine zu hohe Energie und werden normalerweise unter normalen Umständen nicht berücksichtigt. Umgekehrt gibt es sehr niedrige Energiebänder, die mit den Kernorbitalen verbunden sind (wie 1s-Elektronen ). Diese Niedrigenergie - Kernband s auch in der Regel nicht berücksichtigt , da sie mit Elektronen zu jeder Zeit gefüllt bleiben und sind daher inert. Ebenso weisen Materialien in ihrer gesamten Bandstruktur mehrere Bandlücken auf.

Die wichtigsten Banden und Bandlücken – die für Elektronik und Optoelektronik relevant sind – sind solche mit Energien nahe dem Fermi-Niveau. Die Bänder und Bandlücken in der Nähe des Fermi-Niveaus erhalten je nach Material spezielle Namen:

• In einem Halbleiter oder Band Isolator wird das Fermi - Niveau durch einen Bandabstand umgeben ist , bezeichnet als die Bandlücke (es von den anderen Bandlücken in der Bandstruktur zu unterscheiden). Das nächstgelegene Band oberhalb der Bandlücke wird als das Leitungsband , und die nächste Band unterhalb der Bandlücke wird als das Valenzband . Der Name "Valenzband" wurde in Analogie zur Chemie geprägt, da bei Halbleitern (und Isolatoren) das Valenzband aus den Valenzorbitalen aufgebaut ist .
• In einem Metall oder Halbmetall liegt das Fermi-Niveau innerhalb eines oder mehrerer zulässiger Bänder. Bei Halbmetallen werden die Bänder in der Regel als "Leitungsband" oder "Valenzband" bezeichnet, je nachdem, ob der Ladungstransport eher elektronen- oder lochartig ist, analog zu Halbleitern. Bei vielen Metallen sind die Bänder jedoch weder elektronen- noch lochartig und werden oft nur "Valenzband" genannt, da sie aus Valenzorbitalen bestehen. Die Bandlücken in der Bandstruktur eines Metalls sind für die Niederenergiephysik nicht wichtig, da sie zu weit vom Fermi-Niveau entfernt sind.

Theorie in Kristallen

Der Ansatz ist der Spezialfall von Elektronenwellen in einem periodischen Kristallgitter unter Verwendung des Bloch-Theorems, wie es allgemein in der dynamischen Beugungstheorie behandelt wird . Jeder Kristall ist eine periodische Struktur, die durch ein Bravais-Gitter charakterisiert werden kann , und für jedes Bravais-Gitter können wir das reziproke Gitter bestimmen , das die Periodizität in einem Satz von drei reziproken Gittervektoren ( b ₁ , b ₂ , b ₃ ) einkapselt . Nun kann jedes periodische Potential V( r ), das dieselbe Periodizität wie das direkte Gitter hat, als Fourier-Reihe erweitert werden , deren einzige nicht verschwindende Komponenten diejenigen sind, die den reziproken Gittervektoren zugeordnet sind. Die Erweiterung kann also geschrieben werden als:

${\displaystyle V(\mathbf{r})=\sum_{\mathbf{K}} }{V_{\mathbf{K}}e^{i\mathbf{K}\cdot\mathbf{r}}}}$

wobei K = m ₁ b ₁ + m ₂ b ₂ + m ₃ b ₃ für jeden Satz von ganzen Zahlen (m ₁ ,m ₂ ,m ₃ ) ist.

Ausgehend von dieser Theorie kann versucht werden, die Bandstruktur eines bestimmten Materials vorherzusagen, jedoch können die meisten Ab-initio-Methoden für elektronische Strukturberechnungen die beobachtete Bandlücke nicht vorhersagen.

Nahezu freies Elektron-Approximation

Bei der Näherung mit nahezu freien Elektronen werden Wechselwirkungen zwischen Elektronen vollständig vernachlässigt. Diese Näherung erlaubt die Verwendung des Satzes von Bloch, der besagt, dass Elektronen in einem periodischen Potential Wellenfunktionen und Energien haben, die im Wellenvektor bis zu einer konstanten Phasenverschiebung zwischen benachbarten reziproken Gittervektoren periodisch sind. Die Folgen der Periodizität werden mathematisch durch die Satzfunktion von Bloch beschrieben:

${\displaystyle {\Psi}_{n,\mathbf{k}}(\mathbf{r})=e^{i\mathbf{k}\cdot\mathbf{r}}u_{n}(\mathbf{ R} )}$

wobei die Funktion über dem Kristallgitter periodisch ist, d. h. ${\displaystyle u_{n}(\mathbf{r})}$

${\displaystyle u_{n}(\mathbf{r})=u_{n}(\mathbf{rR})}$.

Dabei bezieht sich der Index n auf das n-te Energieband, der Wellenvektor k bezieht sich auf die Bewegungsrichtung des Elektrons, r ist die Position im Kristall und R ist die Position eines Atomplatzes.

Das NFE-Modell funktioniert besonders gut in Materialien wie Metallen, bei denen die Abstände zwischen benachbarten Atomen klein sind. In solchen Materialien ist die Überlappung von Atomorbitalen und -potentialen an benachbarten Atomen relativ groß. In diesem Fall kann die Wellenfunktion des Elektrons durch eine (modifizierte) ebene Welle angenähert werden. Die Bandstruktur eines Metalls wie Aluminium kommt sogar der Leergitter-Näherung nahe .

Modell mit enger Bindung

Das entgegengesetzte Extrem zur Annäherung an nahezu freie Elektronen geht davon aus, dass sich die Elektronen im Kristall wie eine Ansammlung von konstituierenden Atomen verhalten. Dieses enge Bindungsmodell geht davon aus, dass die Lösung der zeitunabhängigen Einelektronen- Schrödinger-Gleichung durch eine Linearkombination von Atomorbitalen gut angenähert wird . ${\displaystyle \Psi}$ ${\displaystyle \psi_{n}(\mathbf{r})}$

${\displaystyle \Psi(\mathbf{r})=\sum_{n,\mathbf{R}}b_{n,\mathbf{R}}\psi_{n}(\mathbf{rR})}$,

wobei die Koeffizienten so gewählt werden, dass sie die beste Näherungslösung dieser Form ergeben. Index n bezieht sich auf ein atomares Energieniveau und R bezieht sich auf eine atomare Stelle. Ein genauerer Ansatz, der diese Idee verwendet, verwendet Wannier-Funktionen , definiert durch: ${\displaystyle b_{n,\mathbf{R}}}$

${\displaystyle a_{n}(\mathbf{rR})={\frac{V_{C}}{(2\pi)^{3}}}\int \limits_{\text{BZ}}d\ mathbf {k} e^{-i\mathbf {k} \cdot (\mathbf {Rr} )}u_{n\mathbf {k}}}$;

wobei der periodische Teil des Bloch-Theorems und das Integral über der Brillouin-Zone liegt . Hier bezieht sich der Index n auf das n- te Energieband im Kristall. Die Wannier-Funktionen sind in der Nähe von Atomzentren lokalisiert, wie Atomorbitale, aber als Bloch-Funktionen definiert, sind sie genau auf Lösungen basierend auf dem Kristallpotential bezogen. Wannierfunktionen auf verschiedenen Atomplätzen R sind orthogonal. Die Wannier-Funktionen können verwendet werden, um die Schrödinger-Lösung für das n- te Energieband zu bilden als: ${\displaystyle u_{n\mathbf {k}}}$

${\displaystyle \Psi_{n,\mathbf{k}}(\mathbf{r})=\sum_{\mathbf{R}}e^{-i\mathbf{k}\cdot (\mathbf {Rr } )}a_{n}(\mathbf{rR})}$.

Das TB-Modell funktioniert gut in Materialien mit begrenzter Überlappung zwischen Atomorbitalen und Potentialen an benachbarten Atomen. Bandstrukturen von Materialien wie Si , GaAs , SiO ₂ und Diamant beispielsweise werden von TB-Hamiltonianern anhand von atomaren sp ³ -Orbitalen gut beschrieben . In Übergangsmetallen wird ein gemischtes TB-NFE-Modell verwendet, um das breite NFE- Leitungsband und die schmalen eingebetteten TB-d-Bänder zu beschreiben. Die radialen Funktionen des Atomorbitalteils der Wannier-Funktionen lassen sich am einfachsten mit Pseudopotentialmethoden berechnen . Als ökonomischer Ausgangspunkt für weitere Berechnungen werden häufig NFE-, TB- oder kombinierte NFE-TB-Bandstrukturberechnungen, manchmal erweitert um Wellenfunktions-Approximationen auf Basis von Pseudopotentialverfahren, verwendet.

KKR-Modell

Die KKR-Methode, auch "Multiple Scattering Theory" oder Green'sche Funktionenmethode genannt, findet die stationären Werte der inversen Übergangsmatrix T statt des Hamilton-Operators. Eine Variationsimplementierung wurde von Korringa , Kohn und Rostocker vorgeschlagen und wird oft als Korringa-Kohn-Rostoker-Methode bezeichnet . Die wichtigsten Merkmale der KKR- oder Greenschen Funktionsformulierung sind: (1) sie trennt die zwei Aspekte des Problems: Struktur (Positionen der Atome) von der Streuung (chemische Identität der Atome); und (2) Greens Funktionen bieten einen natürlichen Ansatz für eine lokalisierte Beschreibung elektronischer Eigenschaften, die an Legierungen und andere ungeordnete Systeme angepasst werden können. Die einfachste Form dieser Näherung zentriert nicht überlappende Kugeln (als Muffinformen bezeichnet ) auf die Atompositionen. Innerhalb dieser Bereiche wird das von einem Elektron erfahrene Potential als kugelsymmetrisch um den gegebenen Kern angenähert. Im verbleibenden Zwischengitterbereich wird das abgeschirmte Potential als Konstante angenähert. Die Kontinuität des Potentials zwischen den atomzentrierten Kugeln und der Zwischengitterregion wird erzwungen.

Dichtefunktionaltheorie

In der neueren Physikliteratur wird eine große Mehrheit der elektronischen Strukturen und Banddiagramme mit Hilfe der Dichtefunktionaltheorie (DFT) berechnet , die kein Modell, sondern eine Theorie ist, dh eine mikroskopische Theorie der ersten Prinzipien der Physik der kondensierten Materie , die versucht das Elektron-Elektron-Vielteilchenproblem durch die Einführung eines Austauschkorrelationsterms in das Funktional der Elektronendichte zu lösen . DFT-berechnete Banden stimmen in vielen Fällen mit experimentell gemessenen Banden überein, beispielsweise durch winkelaufgelöste Photoemissionsspektroskopie (ARPES). Insbesondere die Bandform wird durch DFT typischerweise gut reproduziert. Aber es gibt auch systematische Fehler in DFT-Bändern im Vergleich zu experimentellen Ergebnissen. Insbesondere scheint DFT die Bandlücke in Isolatoren und Halbleitern systematisch um etwa 30-40% zu unterschätzen.

Es wird allgemein angenommen, dass DFT eine Theorie ist, um nur die Grundzustandseigenschaften eines Systems vorherzusagen (zB die Gesamtenergie , die Atomstruktur usw.), und dass die Eigenschaften des angeregten Zustands nicht durch DFT bestimmt werden können. Dies ist ein Missverständnis. Im Prinzip kann die DFT jede Eigenschaft (Grundzustand oder angeregter Zustand) eines Systems bestimmen, wenn ein Funktional gegeben ist, das die Grundzustandsdichte auf diese Eigenschaft abbildet. Dies ist die Essenz des Hohenberg-Kohn-Theorems. In der Praxis existiert jedoch kein bekanntes Funktional, das die Grundzustandsdichte auf Anregungsenergien von Elektronen innerhalb eines Materials abbildet. Was in der Literatur als DFT-Banddiagramm zitiert wird, ist also eine Darstellung der DFT- Kohon-Sham-Energien , dh der Energien eines fiktiven, nicht wechselwirkenden Systems, des Kohn-Sham-Systems, das keinerlei physikalische Interpretation hat. Die elektronische Kohn-Sham-Struktur darf nicht mit der realen elektronischen Quasiteilchen- Struktur eines Systems verwechselt werden, und es gibt kein Koopmans-Theorem für Kohn-Sham-Energien wie für Hartree-Fock-Energien, die man wirklich als eine Näherung für Quasiteilchenenergien . Daher ist die Kohn-Sham-basierte DFT im Prinzip keine Bandtheorie, dh keine Theorie, die sich für die Berechnung von Bändern und Banddiagrammen eignet. Prinzipiell kann zeitabhängige DFT verwendet werden, um die wahre Bandstruktur zu berechnen, obwohl dies in der Praxis oft schwierig ist. Ein beliebter Ansatz ist die Verwendung hybrider Funktionale , die einen Teil des exakten Hartree-Fock-Austauschs beinhalten; dies führt zu einer wesentlichen Verbesserung der vorhergesagten Bandlücken von Halbleitern, ist jedoch für Metalle und Materialien mit großer Bandlücke weniger zuverlässig.

Greensche Funktionsmethoden und die Ab-initio- GW-Approximation

Um die Banden einschließlich der Vielteilcheneffekte der Elektron-Elektron-Wechselwirkung zu berechnen , kann man auf sogenannte Greensche Funktionsmethoden zurückgreifen . Tatsächlich liefert die Kenntnis der Greenschen Funktion eines Systems sowohl Grund- (die Gesamtenergie) als auch Observablen des angeregten Zustands des Systems. Die Pole der Greenschen Funktion sind die Quasiteilchenenergien, die Bänder eines Festkörpers. Die Greensche Funktion kann durch Lösen der Dyson-Gleichung berechnet werden, sobald die Eigenenergie des Systems bekannt ist. Für reale Systeme wie Festkörper ist die Eigenenergie eine sehr komplexe Größe und normalerweise sind Näherungen erforderlich, um das Problem zu lösen. Eine solche Approximation ist die GW-Approximation , die aus der mathematischen Form so genannt wird, nimmt die Selbstenergie als Produkt Σ = GW der Greenschen Funktion G und der dynamisch abgeschirmten Wechselwirkung W an . Dieser Ansatz ist bei der Berechnung von Bandplots (und auch darüber hinausgehenden Größen wie der Spektralfunktion) sachdienlicher und kann auch vollständig ab initio formuliert werden. Die GW-Näherung scheint in Übereinstimmung mit dem Experiment Bandlücken von Isolatoren und Halbleitern zu liefern und damit die systematische DFT-Unterschätzung zu korrigieren.

Dynamische Mean-Field-Theorie

Obwohl die Näherung für nahezu freie Elektronen viele Eigenschaften von Elektronenbandstrukturen beschreiben kann, ist eine Konsequenz dieser Theorie, dass sie die gleiche Anzahl von Elektronen in jeder Elementarzelle vorhersagt. Wenn die Anzahl der Elektronen ungerade ist, würden wir erwarten, dass sich in jeder Elementarzelle ein ungepaartes Elektron befindet und somit das Valenzband nicht vollständig besetzt ist, was das Material zu einem Leiter macht. Materialien wie CoO , die eine ungerade Anzahl von Elektronen pro Elementarzelle aufweisen, sind jedoch Isolatoren, was diesem Ergebnis direkt widerspricht. Diese Art von Material ist als Mott-Isolator bekannt und erfordert die Einbeziehung detaillierter Elektron-Elektron-Wechselwirkungen (die in der Bandtheorie nur als gemittelter Effekt auf das Kristallpotential behandelt werden), um die Diskrepanz zu erklären. Das Hubbard-Modell ist eine ungefähre Theorie, die diese Wechselwirkungen einbeziehen kann. Es kann störungsfrei im Rahmen der sogenannten dynamischen Mean-Field-Theorie behandelt werden , die versucht, die Lücke zwischen der Näherung der nahezu freien Elektronen und dem atomaren Grenzwert zu überbrücken. Formal sind die Zustände in diesem Fall jedoch nicht wechselwirkungsfrei und das Konzept einer Bandstruktur reicht nicht aus, um diese Fälle zu beschreiben.

Andere

Die Berechnung von Bandstrukturen ist ein wichtiges Thema in der theoretischen Festkörperphysik . Neben den oben genannten Modellen umfassen weitere Modelle die folgenden:

• Leergitter-Approximation : die "Bandstruktur" eines Bereichs des freien Raums, der in ein Gitter unterteilt wurde.
• Die k·p-Störungstheorie ist eine Technik, die es ermöglicht, eine Bandstruktur anhand einiger weniger Parameter näherungsweise zu beschreiben. Die Technik wird häufig für Halbleiter verwendet , und die Parameter im Modell werden oft experimentell bestimmt.
• Das Kronig-Penney-Modell , ein eindimensionales rechteckiges Well-Modell, das zur Veranschaulichung der Bandbildung nützlich ist. Obwohl es einfach ist, sagt es viele wichtige Phänomene voraus, ist aber nicht quantitativ.
• Hubbard-Modell

Die Bandstruktur wurde auf Wellenvektoren verallgemeinert, die komplexe Zahlen sind , was zu einer sogenannten komplexen Bandstruktur führt , die an Oberflächen und Grenzflächen von Interesse ist.

Jedes Modell beschreibt einige Arten von Feststoffen sehr gut und andere schlecht. Das Modell der nahezu freien Elektronen funktioniert gut für Metalle, aber schlecht für Nichtmetalle. Das Modell der engen Bindung ist für ionische Isolatoren wie Metallhalogenidsalze (zB NaCl ) äußerst genau .

Banddiagramme

Um zu verstehen, wie sich die Bandstruktur relativ zum Fermi-Niveau im realen Raum ändert, wird ein Bandstrukturplot oft zunächst in Form eines Banddiagramms vereinfacht . In einem Banddiagramm ist die vertikale Achse die Energie, während die horizontale Achse den realen Raum darstellt. Horizontale Linien stellen Energieniveaus dar, während Blöcke Energiebänder darstellen. Wenn die horizontalen Linien in diesem Diagramm geneigt sind, ändert sich die Energie des Niveaus oder Bandes mit der Entfernung. Dies zeigt schematisch das Vorhandensein eines elektrischen Feldes innerhalb des Kristallsystems. Banddiagramme sind nützlich, um die allgemeinen Bandstruktureigenschaften verschiedener Materialien miteinander in Beziehung zu setzen, wenn sie miteinander in Kontakt gebracht werden.

Siehe auch

• Felix Bloch – Pionier der Bandstrukturtheorie
• Alan Herries Wilson – Pionier in der Theorie der Bandstruktur
• Bandlücken-Engineering - der Prozess der Veränderung der Bandstruktur eines Materials

Verweise

Literaturverzeichnis

• Charles Kittel (1996). Einführung in die Festkörperphysik (7. Aufl.). New York: Wiley. ISBN 978-0-471-11181-8.

Weiterlesen

1. Microelectronics , von Jacob Millman und Arvin Gabriel, ISBN  0-07-463736-3 , Tata McGraw-Hill Edition.
2. Festkörperphysik , von Neil Ashcroft und N. David Mermin, ISBN  0-03-083993-9
3. Elementare Festkörperphysik: Prinzipien und Anwendungen , von M. Ali Omar, ISBN  0-201-60733-6
4. Elektronische und optoelektronische Eigenschaften von Halbleiterstrukturen – Kapitel 2 und 3 von Jasprit Singh, ISBN  0-521-82379-X
5. Elektronische Struktur: Grundlegende Theorie und praktische Methoden von Richard Martin, ISBN  0-521-78285-6
6. Physik der kondensierten Materie von Michael P. Marder, ISBN  0-471-17779-2
7. Computational Methods in Solid State Physics von VV Nemoshkalenko und NV Antonov, ISBN  90-5699-094-2
8. Elementare elektronische Struktur von Walter A. Harrison, ISBN  981-238-708-0
9. Pseudopotentiale in der Theorie der Metalle von Walter A. Harrison, WA Benjamin (New York) 1966
10. Tutorial zu Bandstrukturmethoden von Dr. Vasileska (2008)

Externe Links

• Medien im Zusammenhang mit elektronischen Bandstrukturen bei Wikimedia Commons
• Animation, Anwendungen und Forschung zu Quantenphysik und Bandtheorie (Université Paris Sud)