Grenze (Kategorie Theorie) - Limit (category theory)

In der Kategorientheorie , einem Zweig der Mathematik , erfasst der abstrakte Begriff eines Grenzwerts die wesentlichen Eigenschaften universeller Konstruktionen wie Produkte , Pullbacks und inverse Grenzwerte . Die duale Vorstellung eines Kolimes verallgemeinert Konstruktionen wie disjoint Gewerkschaften , direkte Summen , Co - Produkte , Pushouts und direkte Grenzen .

Limits und Colimits, wie die stark verwandten Begriffe von universellen Eigenschaften und adjungierten Funktoren , existieren auf einem hohen Abstraktionsniveau. Um sie zu verstehen, ist es hilfreich, zuerst die spezifischen Beispiele zu studieren, die diese Konzepte verallgemeinern sollen.

Definition

Limits und Colimits in einer Kategorie werden durch Diagramme in definiert . Formal ist ein Diagramm der Form in ein Funktor von bis : ${\displaystyle C}$${\displaystyle C}$${\displaystyle J}$${\displaystyle C}$${\displaystyle J}$${\displaystyle C}$

${\displaystyle F:J\nach C.}$

Die Kategorie wird als Indexkategorie betrachtet , und das Diagramm wird als Indizierung einer Sammlung von Objekten und Morphismen im Muster betrachtet . ${\displaystyle J}$${\displaystyle F}$${\displaystyle C}$${\displaystyle J}$

Am häufigsten interessiert man sich für den Fall, dass die Kategorie eine kleine oder sogar endliche Kategorie ist. Ein Diagramm , wird gesagt, dass kleine oder endliche , wenn ist. ${\displaystyle J}$${\displaystyle J}$

Grenzen

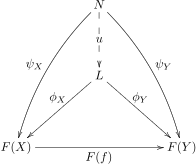
Seien Sie ein Diagramm der Form in einer Kategorie . Ein Kegel to ist ein Objekt von zusammen mit einer Familie von Morphismen, die durch die Objekte von indiziert sind , so dass wir für jeden Morphismus in haben . ${\displaystyle F:J\to C}$${\displaystyle J}$${\displaystyle C}$${\displaystyle F}$${\displaystyle N}$${\displaystyle C}$${\displaystyle \psi_{X}:N\to F(X)}$${\displaystyle X}$${\displaystyle J}$${\displaystyle f:X\to Y}$${\displaystyle J}$${\displaystyle F(f)\circ \psi_{X}=\psi_{Y}}$

Eine Grenze des Diagramms ist ein Kegel zu so, dass für jeden anderen Kegel zu ein eindeutiger Morphismus existiert, so dass für alle in . ${\displaystyle F:J\to C}$${\displaystyle (L,\phi)}$${\displaystyle F}$${\displaystyle (N,\psi)}$${\displaystyle F}$${\displaystyle u:N\nach L}$${\displaystyle \phi_{X}\circ u=\psi_{X}}$${\displaystyle X}$${\displaystyle J}$

Man sagt, dass der Kegel durch den Kegel mit der eindeutigen Faktorisierung faktorisiert . Der Morphismus wird manchmal als vermittelnder Morphismus bezeichnet . ${\displaystyle (N,\psi)}$${\displaystyle (L,\phi)}$${\displaystyle u}$${\displaystyle u}$

Grenzen werden auch als Universalkegel bezeichnet , da sie durch eine universelle Eigenschaft gekennzeichnet sind (weitere Informationen siehe unten). Wie bei jeder universellen Eigenschaft beschreibt die obige Definition einen ausgewogenen Zustand der Allgemeinheit: Das Grenzobjekt muss allgemein genug sein, damit jeder andere Kegel es durchdringen kann; andererseits muss sie hinreichend spezifisch sein, damit für jeden Kegel nur eine solche Faktorisierung möglich ist. ${\displaystyle L}$${\displaystyle L}$

Grenzen können auch als Endobjekte in der Kategorie der Kegel bis F charakterisiert werden .

Es ist möglich, dass ein Diagramm überhaupt keine Begrenzung hat. Wenn ein Diagramm jedoch einen Grenzwert hat, dann ist dieser Grenzwert im Wesentlichen eindeutig: er ist bis auf einen eindeutigen Isomorphismus eindeutig . Aus diesem Grunde spricht man oft von der Grenze von F .

Colimits

Die dualen Begriffe von Grenzen und Kegeln sind Colimits und Co-Kegel. Obwohl es einfach ist, ihre Definitionen durch Invertieren aller Morphismen in den obigen Definitionen zu erhalten, werden wir sie hier explizit angeben:

Ein Co-Kegel eines Diagramms ist ein Objekt von zusammen mit einer Familie von Morphismen ${\displaystyle F:J\to C}$${\displaystyle N}$${\displaystyle C}$

${\displaystyle \psi_{X}:F(X)\to N}$

für jedes Objekt von , so dass für jeden Morphismus in gilt . ${\displaystyle X}$${\displaystyle J}$${\displaystyle f:X\to Y}$${\displaystyle J}$${\displaystyle \psi_{Y}\circ F(f)=\psi_{X}}$

Ein Colimit eines Diagramms ist ein Co-Kegel von derart, dass für jeden anderen Co-Kegel von ein eindeutiger Morphismus existiert, so dass für alle in . ${\displaystyle F:J\to C}$${\displaystyle (L,\phi)}$${\displaystyle F}$${\displaystyle (N,\psi)}$${\displaystyle F}$${\displaystyle u:L\to N}$${\displaystyle u\circ\phi_{X}=\psi_{X}}$${\displaystyle X}$${\displaystyle J}$

Colimits werden auch als universelle Co-Kegel bezeichnet . Sie können als Ausgangsobjekte in der Kategorie der Co-Kegel aus charakterisiert werden . ${\displaystyle F}$

Wenn ein Diagramm wie bei Grenzwerten einen Kolimit hat, dann ist dieser Kolimit bis auf einen eindeutigen Isomorphismus eindeutig. ${\displaystyle F}$

Variationen

Grenzen und Colimits können auch für Sammlungen von Objekten und Morphismen ohne Verwendung von Diagrammen definiert werden. Die Definitionen sind die gleichen (beachten Sie, dass wir in den obigen Definitionen nie die Zusammensetzung von Morphismen in verwenden mussten ). Diese Variation fügt jedoch keine neuen Informationen hinzu. Jede Sammlung von Objekten und Morphismen definiert einen (möglicherweise großen) gerichteten Graphen . Wenn wir die freie Kategorie sein lassen , die von erzeugt wird , gibt es ein universelles Diagramm, dessen Bild enthält . Der Grenzwert (oder Colimit) dieses Diagramms ist derselbe wie der Grenzwert (oder Colimit) der ursprünglichen Sammlung von Objekten und Morphismen. ${\displaystyle J}$ ${\displaystyle G}$${\displaystyle J}$${\displaystyle G}$${\displaystyle F:J\to C}$${\displaystyle G}$

Schwache Grenze und schwache Kogrenzen werden wie Grenzen und Kogrenzen definiert, außer dass die Eindeutigkeitseigenschaft des vermittelnden Morphismus weggelassen wird.

Beispiele

Grenzen

Die Definition von Grenzwerten ist allgemein genug, um mehrere in der Praxis nützliche Konstruktionen zusammenzufassen. Im Folgenden betrachten wir den Grenzwert ( L , φ ) eines Diagramms F  : J → C .

• Terminalobjekte . Wenn J die leere Kategorie ist, gibt es nur ein Diagramm der Form J : das leere (ähnlich der leeren Funktion in der Mengenlehre). Ein Kegel zum leeren Diagramm ist im Wesentlichen nur ein Objekt von C . Der Grenzwert von F ist jedes Objekt, das von jedem anderen Objekt eindeutig durchfaktoriert wird. Dies ist nur die Definition eines Terminalobjekts .
• Produkte . Wenn J a diskrete Kategorie dann ein Diagramm F istWesentlichen nichtsals eine Familie von Objekten von C , indiziert durch J . Der Limes L von F heißt das Produkt dieser Objekte. Der Kegel φ besteht aus einer Familie von Morphismen φ _X  : L → F ( X ), die als Projektionen des Produkts bezeichnet werden. In der Kategorie der Mengen zum Beispiel sind die Produkte durch kartesische Produkte gegeben und die Projektionen sind nur die natürlichen Projektionen auf die verschiedenen Faktoren.
  • Befugnisse . Ein Spezialfall eines Produkts liegt vor, wenn das Diagramm F ein konstanter Funktor zu einem Objekt X von C ist . Der Grenzwert dieses Diagramms wird als J- ^te Potenz von X bezeichnet und mit X ^{J bezeichnet} .
• Equalizer . Wenn J eine Kategorie mit zwei Objekten und zwei parallelen Morphismen von einem Objekt zum anderen ist, dann ist ein Diagramm der Form J ein Paar paralleler Morphismen in C . Der Grenzwert L eines solchen Diagramms wird als Entzerrer dieser Morphismen bezeichnet.
  • Kerne . Ein Kernel ist ein Spezialfall eines Equalizers, bei dem einer der Morphismen ein Null-Morphismus ist .
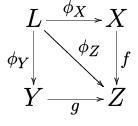
• Rückschläge . Sei F ein Diagramm, das drei Objekte X , Y und Z in C auswählt , wobei die einzigen Nichtidentitätsmorphismen f  : X → Z und g  : Y → Z sind . Der Grenzwert L von F wird Pullback oder Faserprodukt genannt . Man kann es sich schön als kommutatives Quadrat vorstellen :

• Inverse Grenzen . Lassen J eine sein gerichtete Menge (als kleine Kategorie betrachtet durch Hinzufügen Pfeile i → j , wenn und nur wenn i ≥ j ) und lassen F  : J ^op → C ein Diagramm sein. Der Grenzwert von F wird (verwirrenderweise) als inverser Grenzwert oder projektiver Grenzwert bezeichnet .
• Wenn J = 1 , die Kategorie mit einem einzelnen Objekt und Morphismus, dann ist ein Diagramm der Form J im Wesentlichen nur ein Objekt X von C . Ein Kegel zu einem Objekt X ist nur ein Morphismus mit Kodomäne X . Ein Morphismus f  : Y → X ist genau dann ein Grenzwert des Diagramms X, wenn f ein Isomorphismus ist . Allgemeiner gesagt, wenn J eine beliebige Kategorie mit einem Anfangsobjekt i ist , dann hat jedes Diagramm der Form J eine Grenze, nämlich jedes zu F ( i ) isomorphe Objekt . Ein solcher Isomorphismus bestimmt eindeutig einen Universalkegel zu F .
• Topologische Grenzen . Funktionsgrenzen sind ein Sonderfall von Filtergrenzen , die sich wie folgt auf kategoriale Grenzen beziehen. Gegeben einen topologischen Raum X , bezeichne mit F die Filtermenge auf X , x ∈ X einen Punkt, V ( x ) ∈ F das Nachbarschaftsfilter von x , A ∈ F ein bestimmtes Filter und die Filtermenge feiner als A und das gegen x konvergieren . Die Filter F sind eine kleine und dünne Kategoriestruktur gegeben durch Zugabe von einem Pfeil A → B , wenn und nur wenn A ⊆ B . Die Injektion wird zum Funktor und es gilt folgende Äquivalenz:${\displaystyle F_{x,A}=\{G\in F\mid V(x)\cup A\Teilmenge G\}}$${\displaystyle I_{x,A}:F_{x,A}\to F}$

x ist ein topologischer Grenzwert von A genau dann, wenn A ein kategorialer Grenzwert von ist${\displaystyle I_{x,A}}$

Colimits

Beispiele für Colimits werden durch die dualen Versionen der obigen Beispiele gegeben:

• Ausgangsobjekte sind Colimits von leeren Diagrammen.
• Co - Produkte sind Colimites von Diagrammen durch diskrete Kategorien indiziert.
  • Copowers sind Colimits konstanter Diagramme aus diskreten Kategorien.
• Co-Entzerrer sind Colimits eines parallelen Morphismenpaares.
  • Cokernels sind Ko-Entzerrer eines Morphismus und eines parallelen Null-Morphismus.
• Pushouts sind Colimits eines Morphismenpaares mit gemeinsamer Domäne.
• Direkte Grenzen sind Colimits von Diagrammen, die durch gerichtete Mengen indiziert sind.

Eigenschaften

Existenz von Grenzen

Ein gegebenes Diagramm F  : J → C kann eine Grenze (oder Co-Grenze) in C haben oder nicht . Tatsächlich kann es nicht einmal einen Kegel zu F geben , geschweige denn einen universellen Kegel.

Eine Kategorie C heißt Grenzwerte der Form J, wenn jedes Diagramm der Form J einen Grenzwert in C hat . Insbesondere wird eine Kategorie C soll

• Produkte haben, wenn sie Grenzen der Form J für jede kleine diskrete Kategorie J hat (sie braucht keine großen Produkte zu haben),
• Equalizer haben, wenn es Formgrenzen hat (dh jedes parallele Paar von Morphismen hat einen Equalizer),${\displaystyle \bullet \rightrightarrows \bullet}$
• haben Pullbacks, wenn es Formgrenzen hat (dh jedes Morphismenpaar mit gemeinsamer Codomäne hat einen Pullback).${\displaystyle \bullet \rightarrow \bullet \leftarrow \bullet}$

Eine vollständige Kategorie ist eine Kategorie, die alle kleinen Grenzen hat (dh alle Grenzen der Form J für jede kleine Kategorie J ).

Man kann auch die dualen Definitionen machen. Eine Kategorie hat Colimits der Form J, wenn jedes Diagramm der Form J einen Colimit in C hat . Eine cocomplete Kategorie ist eine Kategorie , die alle kleinen Colimits enthält.

Der Existenzsatz für Grenzen besagt, dass wenn eine Kategorie C Entzerrer und alle Produkte hat, die durch die Klassen Ob( J ) und Hom( J ) indiziert sind , dann C alle Grenzen der Form J hat . In diesem Fall lässt sich der Grenzwert eines Diagramms F  : J → C als Entzerrer der beiden Morphismen konstruieren

${\displaystyle s,t:\prod_{i\in\operatorname {Ob} (J)}F(i)\rightarrows \prod_{f\in \operatorname {Hom} (J)}F(\operatorname { Kabeljau} (f))}$

gegeben (in Komponentenform) durch

${\displaystyle {\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatorname {dom} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}\\t&={\bigl (}\pi_{\operatorname {cod} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}.\end{aligned }}}$

Es gibt ein duales Existenztheorem für Colimits im Sinne von Co-Entzerrern und Co-Produkten. Beide Sätze geben hinreichende und notwendige Bedingungen für die Existenz aller (Co)Grenzen der Form J .

Universelles Eigentum

Limits und Colimits sind wichtige Spezialfälle universeller Konstruktionen .

Sei C eine Kategorie und sei J eine kleine Indexkategorie. Die Funktorkategorie C ^J kann man sich als die Kategorie aller Diagramme der Form J in C vorstellen . Der Diagonalfunktor

${\displaystyle \Delta:{\mathcal{C}}\to {\mathcal{C}}^{\mathcal{J}}}$

ist der Funktors dass jedes Objekt abbildet N in C mit dem konstanten Funktors Δ ( N ): J → C zu N . Das heißt, Δ ( N ) ( X ) = N für jedes Objekt X in J und Δ ( N ) ( f ) = id _N für jeden morphism f in J .

Gegeben ein Diagramm F : J → C (als Objekt in C ^J gedacht ), ist eine natürliche Transformation ψ  : Δ( N ) → F (die nur ein Morphismus in der Kategorie C ^{J ist} ) dasselbe wie ein Kegel aus N bis F . Um dies zu sehen, beachten Sie zunächst, dass Δ( N )( X ) = N für alle X impliziert, dass die Komponenten von ψ Morphismen ψ _X  : N → F ( X ) sind, die alle den Definitionsbereich N teilen . Darüber hinaus ist die Forderung, dass die Diagramme des Kegels kommutieren, einfach deshalb wahr, weil dieses ψ eine natürliche Transformation ist. (Dual ist eine natürliche Transformation ψ  : F → Δ( N ) dasselbe wie ein Co-Kegel von F nach N .)

Daher können die Definitionen von Limits und Colimits dann in der Form neu formuliert werden:

• Ein Grenzwert von F ist ein universeller Morphismus von Δ nach F .
• Ein Colimit von F ist ein universeller Morphismus von F nach Δ.

Zusätze

Wie alle universellen Konstruktionen ist die Bildung von Grenzen und Colimits funktionaler Natur. Mit anderen Worten, wenn jedes Diagramm der Form J einen Grenzwert in C hat (für J klein), existiert ein Grenzwertfunktor

${\displaystyle \lim :{\mathcal{C}}^{\mathcal{J}}\to {\mathcal{C}}}$

die jedem Diagramm seinen Grenzwert und jeder natürlichen Transformation η : F → G den eindeutigen Morphismus lim η : lim F → lim G zuordnet, der mit den entsprechenden Universalkegeln kommutiert. Dieser Funktor ist rechts adjoint zum Diagonalfunktor Δ: C → C ^J . Diese Adjunktion liefert eine Bijektion zwischen der Menge aller Morphismen von N bis lim F und der Menge aller Kegel von N bis F

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \operatorname {Kegel} (N,F)}$

was in den Variablen N und F natürlich ist . Die Anzahl dieser Adjunktion ist einfach der Universalkegel von lim F bis F . Wenn die Indexkategorie J ist verbunden (und nicht leer) , wird die Einheit der adjunction ein Isomorphismus so daß lim eine linke Inverse von Δ ist. Dies schlägt fehl, wenn J nicht verbunden ist. Wenn beispielsweise J eine diskrete Kategorie ist, sind die Komponenten der Einheit die Diagonalmorphismen δ : N → N ^J .

Dual, wenn jedes Diagramm der Form J einen Colimit in C hat (für J klein), existiert ein Colimitfunktor

${\displaystyle \operatorname {colim} :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}}$

die jedem Diagramm sein Colimit zuweist. Dieser Funktor bleibt adjungiert zum Diagonalfunktor Δ : C → C ^J , und man hat einen natürlichen Isomorphismus

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \operatorname {Cocone} (F,N).}$

Die Einheit dieser Adjunktion ist der universelle Kokon von F bis Colim F . Wenn J zusammenhängend (und nicht leer) ist, dann ist die Countite ein Isomorphismus, so dass Colim eine Linksinverse von Δ ist.

Beachten Sie, dass sowohl der Grenzwert- als auch der Kolimit-Funktor kovariante Funktoren sind.

Als Repräsentationen von Funktoren

Man kann Hom-Funktoren verwenden , um Limits und Colimits in einer Kategorie C mit Limits in Set , der Kategorie der Mengen, in Beziehung zu setzen . Dies folgt zum Teil aus der Tatsache, dass der kovariante Hom-Funktor Hom( N , –) : C → Set alle Grenzen in C beibehält . Durch die Dualität muss der kontravariante Hom-Funktor Colimits zu Limits bringen.

Hat ein Diagramm F  : J → C einen Grenzwert in C , bezeichnet mit lim F , dann gibt es einen kanonischen Isomorphismus

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \lim \operatorname {Hom} (N,F-)}$

was in der Variablen N natürlich ist . Dabei ist der Funktor Hom( N , F –) die Zusammensetzung des Hom-Funktors Hom( N , –) mit F . Dieser Isomorphismus ist der einzige, der die Grenzkegel respektiert.

Man kann die obige Beziehung verwenden, um den Grenzwert von F in C zu definieren . Der erste Schritt ist zu beachten, dass der Grenzwert des Funktors Hom( N , F –) mit der Menge aller Kegel von N bis F identifiziert werden kann :

${\displaystyle \lim \operatorname {Hom} (N,F-)=\operatorname {Kegel} (N,F).}$

Der Grenzkegel ist gegeben durch die Familie der Abbildungen π _X  : Kegel( N , F ) → Hom( N , FX ) wobei π _X ( ψ ) = ψ _X . Ist ein Objekt L von C zusammen mit einem natürlichen Isomorphismus Φ  : Hom(–, L ) → Cone(–, F ) gegeben, so ist das Objekt L ein Grenzwert von F mit dem Grenzkegel _L (id _L ). In der Phantasie läuft dies darauf hinaus, dass ein Grenzwert von F eine Darstellung des Funktors Cone(–, F ) : C → Set ist .

Wenn ein Diagramm F  : J → C einen Colimit in C hat , bezeichnet als Colim F , gibt es einen eindeutigen kanonischen Isomorphismus

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \lim \operatorname {Hom} (F-,N)}$

was in der Variablen N natürlich ist und die zusammengrenzenden Kegel respektiert. Indem man den Grenzwert von Hom( F –, N ) mit der Menge Cocone( F , N ) identifiziert , kann diese Beziehung verwendet werden, um den Kolimit des Diagramms F als Darstellung des Funktors Cocone( F , –) zu definieren.

Austausch von Limits und Colimits von Sets

Sei I eine endliche Kategorie und J eine kleine gefilterte Kategorie . Für jeden Bifunktor

${\displaystyle F:I\times J\to\mathbf {Set} ,}$

es gibt einen natürlichen Isomorphismus

${\displaystyle \operatorname {colim} \limits_{J}\lim_{I}F(i,j)\rightarrow \lim_{I}\operatorname {colim} \limits_{J}F(i,j ).}$

In Worten, gefilterte Colimits in Set pendeln mit endlichen Grenzen. Es gilt auch, dass kleine Grenzen mit kleinen Grenzen pendeln.

Funktionen und Grenzen

Wenn F  : J → C ein Diagramm in C und G  : C → D ein Funktor ist, dann erhält man durch Komposition (erinnern Sie sich daran, dass ein Diagramm nur ein Funktor ist) ein Diagramm GF  : J → D . Eine natürliche Frage ist dann:

„Wie hängen die Grenzen von GF mit denen von F zusammen ?“

Einhaltung von Grenzen

Ein Funktor G  : C → D induziert eine Abbildung von Cone( F ) nach Cone( GF ): wenn Ψ ein Kegel von N nach F ist, dann ist GΨ ein Kegel von GN nach GF . Der Funktor G soll die Grenzen von F bewahren, wenn ( GL , Gφ ) ein Grenzwert von GF ist, wann immer ( L , φ ) ein Grenzwert von F ist . (Beachten Sie, dass , wenn der Grenzwert von F nicht vorhanden ist, dann G vacuously bewahrt die Grenzen von F .)

Ein Funktor G behält alle Grenzen der Form J, wenn er die Grenzen aller Diagramme F  : J → C erhält . Zum Beispiel kann man sagen, dass G Produkte, Equalizer, Pullbacks usw. erhält . Ein kontinuierlicher Funktor ist einer, der alle kleinen Grenzen beibehält.

Für Colimits kann man analoge Definitionen treffen. Zum Beispiel bewahrt ein Funktor G die Colimits von F, wenn G ( L , φ ) ein Colimit von GF ist, wann immer ( L , φ ) ein Colimit von F ist . Ein kokontinuierlicher Funktor ist einer, der alle kleinen Colimits beibehält.

Wenn C eine vollständige Kategorie ist , dann ist nach obigem Existenzsatz für Grenzwerte ein Funktor G  : C → D genau dann stetig, wenn er (kleine) Produkte und Entzerrer erhält. Dual ist G genau dann kokontinuierlich, wenn es (kleine) Koprodukte und Koentzerrer erhält.

Eine wichtige Eigenschaft von adjungierten Funktoren ist, dass jeder rechtsadjungierte Funktor stetig und jeder linksadjungierte Funktor kostetig ist. Da adjungierte Funktoren in Hülle und Fülle existieren, gibt dies zahlreiche Beispiele für stetige und kokontinuierliche Funktoren.

Für ein gegebenes Diagramm F  : J → C und Funktor G  : C → D , wenn sowohl F als auch GF spezifizierte Grenzen haben, gibt es einen eindeutigen kanonischen Morphismus

${\displaystyle \tau_{F}:G\lim F\to \lim GF}$

die die entsprechenden Grenzkegel respektiert. Der Funktor G erhält die Grenzen von F genau dann, wenn diese Abbildung ein Isomorphismus ist. Wenn die Kategorien C und D alle Grenzen der Form J haben, dann ist lim ein Funktor und die Morphismen τ _F bilden die Komponenten einer natürlichen Transformation

${\displaystyle \tau :G\lim\to\lim G^{J}.}$

Der Funktor G behält alle Grenzen der Form J genau dann, wenn τ ein natürlicher Isomorphismus ist. In diesem Sinne kann man sagen , dass der Funktor G mit Grenzen kommutiert ( bis auf einen kanonischen natürlichen Isomorphismus).

Die Erhaltung von Limits und Colimits ist ein Konzept, das nur für kovariante Funktoren gilt. Für kontravariante Funktoren wären die entsprechenden Begriffe ein Funktor, der Colimits auf Limits setzt, oder einer, der Limits auf Colimits setzt.

Aufhebung von Grenzen

A Funktors G  : C → D wird zu der Hebe Grenzen für ein Diagramm F  : J → C , wenn immer dann , wenn ( L , φ ) ist eine Grenze von GF es eine Grenze (existiert L ', φ ') von F , so dass G ( L , φ ′) = ( L , φ ). Ein Funktor G hebt die Grenzen der Form J auf, wenn er die Grenzen für alle Diagramme der Form J aufhebt . Man kann also von Lifting-Produkten, Equalizern, Pullbacks usw. sprechen. Schließlich sagt man, dass G Grenzen aufhebt, wenn es alle Grenzen aufhebt. Es gibt zwei Definitionen für die Aufhebung von Colimits.

Ein Funktor G hebt Grenzen für ein Diagramm F eindeutig auf, wenn es einen eindeutigen Urbildkegel ( L ′, φ ′) gibt, so dass ( L ′, φ ′) ein Grenzwert von F ist und G ( L ′, φ ′) = ( L , φ ). Man kann zeigen, dass G Grenzen genau dann und nur dann aufhebt, wenn es Grenzen aufhebt und amnestisch ist .

Das Aufheben von Grenzen ist eindeutig mit der Einhaltung von Grenzen verbunden. Wenn G Grenzen für ein Diagramm F aufhebt und GF einen Grenzwert hat, dann hat auch F einen Grenzwert und G behält die Grenzen von F bei . Es folgt dem:

• Wenn G die Grenzen aller Form J aufhebt und D alle Grenzen der Form J hat , dann hat C auch alle Grenzen der Form J und G behält diese Grenzen bei.
• Wenn G alle kleinen Grenzen aufhebt und D vollständig ist, dann ist auch C vollständig und G ist stetig.

Die dualen Aussagen für colimits sind gleichermaßen gültig.

Grenzen schaffen und reflektieren

Sei F  : J → C ein Diagramm. Ein Funktor G  : C → D heißt

• erzeuge Grenzen für F, wenn immer ( L , φ ) ein Grenzwert von GF ist, es einen eindeutigen Kegel ( L ′, φ ′) zu F gibt, so dass G ( L ′, φ ′) = ( L , φ ), und außerdem dieser Kegel ist eine Grenze von F .
• reflektiere Grenzen für F, wenn jeder Kegel zu F, dessen Bild unter G eine Grenze von GF ist, bereits eine Grenze von F ist .

Dual kann man Kreation und Reflexion von Colimits definieren.

Die folgenden Aussagen sind leicht als gleichwertig anzusehen:

• Der Funktor G schafft Grenzen.
• Der Funktor G hebt Grenzen auf einzigartige Weise auf und spiegelt Grenzen wider.

Es gibt Beispiele für Funktoren, die Grenzen eindeutig aufheben, aber weder erzeugen noch reflektieren.

Beispiele

• Jeder darstellbare Funktor C → Set behält Limits (aber nicht notwendigerweise Colimits). Insbesondere gilt dies für jedes Objekt A von C für den kovarianten Hom-Funktor Hom( A ,–) : C → Set .
• Der vergessliche Funktor U  : Grp → Set erzeugt (und behält ) alle kleinen Grenzen und gefilterten Colimits ; jedoch U nicht beibehalten Koprodukte. Diese Situation ist typisch für algebraische Vergesslichkeitsfunktoren.
• Der freie Funktor F  : Menge → Grp (der jeder Menge S die freie Gruppe über S zuordnet ) bleibt adjungiert zum Vergessensfunktor U und ist daher kokontinuierlich. Dies erklärt, warum das freie Produkt zweier freier Gruppen G und H die freie Gruppe ist, die durch die disjunkte Vereinigung der Generatoren von G und H erzeugt wird .
• Der Inklusionsfunktor Ab → Grp schafft Grenzen, bewahrt aber keine Koppelprodukte (das Koppelprodukt zweier abelscher Gruppen ist die direkte Summe ).
• Der vergessliche Funktor Top → Set hebt Limits und Colimits auf einzigartige Weise an, schafft aber keines davon.
• Sei Met _c die Kategorie der metrischen Räume mit stetigen Funktionen für Morphismen. Der Vergesslichkeitsfunktor Met _c → Set hebt endliche Grenzen auf, aber nicht eindeutig.

Ein Hinweis zur Terminologie

Ältere Terminologie bezeichnete Grenzen als "inverse Grenzen" oder "projektive Grenzen" und Colimits als "direkte Grenzen" oder "induktive Grenzen". Dies hat zu viel Verwirrung geführt.

Es gibt mehrere Möglichkeiten, sich an die moderne Terminologie zu erinnern. Zuerst,

• Kokerne,
• Nebenprodukte,
• Co-Equalizer und
• Codomains

sind Arten von Colimits, während

• Kerne,
• Produkte
• Equalizer und
• Domänen

sind Arten von Grenzen. Zweitens bedeutet das Präfix "co" "erste Variable von ". Begriffe wie "Kohomologie" und "Kofibration" haben alle eine etwas stärkere Assoziation mit der ersten Variablen, dh der kontravarianten Variablen, des Bifunktors. ${\displaystyle \operatorname {Hom} }$${\displaystyle \operatorname {Hom} }$

Siehe auch

• Kartesische geschlossene Kategorie  – Art der Kategorie in der Kategorientheorie
• Equalizer (Mathematik)  – Satz von Argumenten, bei denen zwei oder mehr Funktionen den gleichen Wert haben
• Inverser Grenzwert  – Konstruktion in der Kategorientheorie
• Produkt (Kategorientheorie)  – Verallgemeinertes Objekt in der Kategorientheorie

Verweise

• Adamek, Jiří; Horst Herrlich; George E. Strecker (1990). Abstrakte und konkrete Kategorien (PDF) . John Wiley & Söhne. ISBN 0-471-60922-6.
• Mac Lane, Saunders (1998). Kategorien für den arbeitenden Mathematiker . Abschlusstexte der Mathematik . 5 (2. Aufl.). Springer-Verlag . ISBN 0-387-98403-8. Zbl  0906.18001 .
• Borceux, Franz (1994). "Grenzen". Handbuch der kategorialen Algebra . Enzyklopädie der Mathematik und ihrer Anwendungen 50-51, 53 [dh 52]. Band 1. Cambridge University Press. ISBN 0-521-44178-1. |volume=hat zusätzlichen Text ( Hilfe )

Externe Links

• Interaktive Webseite , die Beispiele für Limits und Colimits in der Kategorie der endlichen Mengen generiert. Geschrieben von Jocelyn Paine .
• Limit in nLab