Kerr-Metrik - Kerr metric

Generelle Relativität
${\displaystyle G_{\mu\nu}+\Lambda g_{\mu\nu}={8\pi G\over c^{4}}T_{\mu\nu}}$
Einführung Geschichte Mathematische Formulierung Tests
Grundsätzliche Konzepte Äquivalenzprinzip Spezielle Relativität Weltlinie Pseudo-Riemannsche Mannigfaltigkeit
Phänomene Kepler-Problem Gravitationslinsen Gravitationswellen Frame-Ziehen Geodätischer Effekt Ereignishorizont Singularität Schwarzes Loch Freizeit Raumzeit-Diagramme Minkowski-Raumzeit Einstein–Rosen-Brücke
Gleichungen Formalismen Gleichungen Linearisierte Schwerkraft Einstein-Feldgleichungen Friedmann Geodäten Mathisson–Papapetrou–Dixon Hamilton–Jacobi–Einstein Formalismen ADM BSSN Post-Newton Fortgeschrittene Theorie Kaluza-Klein-Theorie Quantengravitation
Lösungen Schwarzschild ( Innenraum ) Reissner–Nordström Gödel Kerr Kerr-Newman Kasner Lemaître–Tolman Taub-NUT Milne Robertson-Walker pp-Welle van Stockum Staub Weyl−Lewis−Papapetrou
Wissenschaftler Einstein Lorentz Hilbert Poincaré Schwarzschild de Sitter Reissner Nordström Weyl Eddington Friedman Milne Zwicky Lemaître Gödel Wheeler Robertson Bardeen Gehhilfe Kerr Chandrasekhar Ehlers Penrose Hawking Raychaudhuri Taylor Hulse van Stockum Taub Neuer Mann Yau Dorn Andere
Physikportal  Kategorie
v T e

Die Kerr-Metrik oder Kerr-Geometrie beschreibt die Geometrie der leeren Raumzeit um ein rotierendes ungeladenes axialsymmetrisches Schwarzes Loch mit einem quasisphärischen Ereignishorizont . Die Kerr- Metrik ist eine exakte Lösung der Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie ; Diese Gleichungen sind stark nichtlinear , was es sehr schwierig macht, exakte Lösungen zu finden.

Überblick

Die Kerr-Metrik ist eine Verallgemeinerung der 1915 von Karl Schwarzschild entdeckten Schwarzschild-Metrik auf einen rotierenden Körper , die die Geometrie der Raumzeit um einen ungeladenen, kugelsymmetrischen und nicht rotierenden Körper beschrieb. Die entsprechende Lösung für einen geladenen , kugelförmigen, nicht rotierenden Körper, die Reissner-Nordström-Metrik , wurde bald darauf (1916–1918) entdeckt. Die genaue Lösung für ein ungeladenes, rotierendes Schwarzes Loch, die Kerr-Metrik, blieb jedoch bis 1963 ungelöst, als sie von Roy Kerr entdeckt wurde . Die natürliche Erweiterung zu einem geladenen, rotierenden Schwarzen Loch, die Kerr-Newman-Metrik , wurde kurz darauf 1965 entdeckt. Diese vier verwandten Lösungen können in der folgenden Tabelle zusammengefasst werden:

wo Q steht für die körpereigene elektrische Ladung und J steht für seinen Spindrehimpuls .

Nach der Kerr-Metrik sollte ein rotierender Körper Frame-Dragging (auch bekannt als Lense-Thirring-Präzession ) aufweisen, eine charakteristische Vorhersage der allgemeinen Relativitätstheorie. Die erste Messung dieses Frame-Dragging-Effekts wurde 2011 durch das Experiment Gravity Probe B durchgeführt. Grob gesagt sagt dieser Effekt voraus, dass Objekte, die sich einer rotierenden Masse nähern, an ihrer Rotation beteiligt werden, nicht aufgrund einer spürbaren Kraft oder eines Drehmoments, sondern aufgrund der wirbelnden Krümmung der Raumzeit selbst, die mit rotierenden Körpern verbunden ist . Im Fall eines rotierenden Schwarzen Lochs, in der Nähe genug Entfernungen, alle Objekte - auch Licht - Muss drehen mit dem schwarzen Loch; der Bereich, in dem dies gilt, wird Ergosphäre genannt .

Das Licht von weit entfernten Quellen kann den Ereignishorizont mehrmals umrunden (wenn nahe genug); Erstellen mehrerer Bilder desselben Objekts . Für einen entfernten Betrachter nimmt der scheinbare senkrechte Abstand zwischen Bildern um einen Faktor von e ^{2 π} (etwa 500) ab. Schnell drehende Schwarze Löcher haben jedoch einen geringeren Abstand zwischen Multiplizitätsbildern.

Rotierende Schwarze Löcher haben Oberflächen, auf denen die Metrik scheinbare Singularitäten zu haben scheint ; Die Größe und Form dieser Oberflächen hängt von der Masse und dem Drehimpuls des Schwarzen Lochs ab . Die äußere Oberfläche umschließt die Ergosphäre und hat eine Form ähnlich einer abgeflachten Kugel. Die innere Oberfläche markiert den Ereignishorizont ; Objekte, die in das Innere dieses Horizonts gelangen, können nie wieder mit der Welt außerhalb dieses Horizonts kommunizieren. Keine der Oberflächen ist jedoch eine echte Singularität, da ihre scheinbare Singularität in einem anderen Koordinatensystem eliminiert werden kann . Objekte zwischen diesen beiden Oberflächen müssen, wie oben erwähnt, mit dem rotierenden Schwarzen Loch mitrotieren; diese Eigenschaft kann im Prinzip verwendet werden, um einem rotierenden Schwarzen Loch Energie bis zu seiner invarianten Massenenergie Mc ² zu entziehen .

Das 2016 angekündigte LIGO-Experiment, das erstmals Gravitationswellen entdeckte, lieferte auch die erste direkte Beobachtung eines Paares schwarzer Kerr-Löcher.

Metrisch

Die Kerr-Metrik wird üblicherweise in einer von zwei Formen ausgedrückt, der Boyer-Lindquist-Form und der Kerr-Schild-Form. Sie kann leicht aus der Schwarzschild-Metrik abgeleitet werden, indem der Newman-Janis-Algorithmus von Newman-Penrose-Formalismus (auch bekannt als Spin-Koeffizient-Formalismus), Ernst-Gleichung oder Ellipsoid-Koordinatentransformation verwendet wird.

Boyer–Lindquist-Koordinaten

Die Kerr-Metrik beschreibt die Geometrie der Raumzeit in der Nähe einer mit Drehimpuls rotierenden Masse . Die Metrik (oder äquivalent ihr Linienelement für die Eigenzeit ) in Boyer-Lindquist-Koordinaten ist ${\displaystyle M}$ ${\displaystyle J}$

${\displaystyle {\begin{aligned}ds^{2}&=-c^{2}d\tau ^{2}\\&=-\left(1-{\frac {r_{s}r}{ \Sigma}}\right)c^{2}dt^{2}+{\frac {\Sigma}{\Delta}}dr^{2}+\Sigma d\theta^{2}+\left(r ^{2}+a^{2}+{\frac{r_{s}ra^{2}}{\Sigma}}\sin^{2}\theta\right)\sin^{2}\theta\ d\phi ^{2}-{\frac {2r_{s}ra\sin^{2}\theta }{\Sigma}}cdt\,d\phi \end{ausgerichtet}}}$

( 1 )

wobei die Koordinaten standardmäßige abgeplattete Sphäroidkoordinaten sind , die den kartesischen Koordinaten entsprechen ${\displaystyle r,\theta,\phi}$

${\displaystyle x={\sqrt {r^{2}+a^{2}}}\sin\theta\cos\phi}$

( 2 )

${\displaystyle y={\sqrt {r^{2}+a^{2}}}\sin\theta\sin\phi}$

( 3 )

${\displaystyle z=r\cos\theta ,}$

( 4 )

wo ist der Schwarzschildradius${\displaystyle r_{s}}$

${\displaystyle r_{s}={\frac {2GM}{c^{2}}},}$

( 5 )

und wo der Kürze halber die Längenskalen und eingeführt wurden als ${\displaystyle a,\Sigma}$${\displaystyle \Delta}$

${\displaystyle a={\frac {J}{Mc}},}$

( 6 )

${\displaystyle \Sigma =r^{2}+a^{2}\cos^{2}\theta,}$

( 7 )

${\displaystyle \Delta =r^{2}-r_{s}r+a^{2}.}$

( 8 )

Ein wichtiges Merkmal in der obigen Metrik ist der Kreuzproduktterm. Dies impliziert, dass es eine Kopplung zwischen Zeit und Bewegung in der Rotationsebene gibt, die verschwindet, wenn der Drehimpuls des Schwarzen Lochs gegen Null geht. ${\displaystyle dt\,d\phi .}$

In der nicht-relativistischen Grenze, wo (oder äquivalent ) gegen Null geht, wird die Kerr-Metrik zur orthogonalen Metrik für die abgeplatteten Sphäroidkoordinaten${\displaystyle M}$${\displaystyle r_{s}}$

${\displaystyle g\mathop {\longrightarrow} _{M\to 0}-c^{2}dt^{2}+{\frac {\Sigma}{r^{2}+a^{2}}} dr^{2}+\Sigma d\theta^{2}+\left(r^{2}+a^{2}\right)\sin^{2}\theta d\phi^{2}}$

( 9 )

Kerr-Schild-Koordinaten

Die Kerr-Metrik kann in der Form "Kerr-Schild" ausgedrückt werden , indem ein bestimmter Satz kartesischer Koordinaten wie folgt verwendet wird. Diese Lösungen wurden 1965 von Kerr und Schild vorgeschlagen .

${\displaystyle g_{\mu\nu}=\eta_{\mu\nu}+fk_{\mu}k_{\nu}\!}$

( 10 )

${\displaystyle f={\frac {2GMr^{3}}{r^{4}+a^{2}z^{2}}}}$

( 11 )

${\displaystyle \mathbf {k} =(k_{x},k_{y},k_{z})=\left({\frac {rx+ay}{r^{2}+a^{2}} },{\frac {ry-ax}{r^{2}+a^{2}}},{\frac {z}{r}}\right)}$

( 12 )

${\displaystyle k_{0}=1.\!}$

( 13 )

Beachten Sie, dass k ein Einheitsvektor ist . Hier ist M die konstante Masse des sich drehenden Objekts, η ist der Minkowski-Tensor und a ist ein konstanter Rotationsparameter des sich drehenden Objekts. Es versteht sich, dass der Vektor entlang der positiven z-Achse gerichtet ist. Die Größe r ist nicht der Radius, sondern implizit definiert durch ${\displaystyle {\vec {a}}}$

${\displaystyle {\frac {x^{2}+y^{2}}{r^{2}+a^{2}}}+{\frac {z^{2}}{r^{2} }}=1}$

( 14 )

Beachten Sie, dass die Größe r zum üblichen Radius R . wird

${\displaystyle r\to R={\sqrt {x^{2}+y^{2}+z^{2}}}}$

wenn der Rotationsparameter a gegen Null geht. Bei dieser Lösungsform werden Einheiten so gewählt, dass die Lichtgeschwindigkeit eins ist ( c = 1). Bei großen Entfernungen von der Quelle ( R ≫ a ) reduzieren sich diese Gleichungen auf die Eddington-Finkelstein-Form der Schwarzschild-Metrik .

In der Kerr-Schild-Form der Kerr-Metrik ist die Determinante des metrischen Tensors überall gleich negativ, auch in der Nähe der Quelle.

Soliton-Koordinaten

Da die Kerr-Metrik (zusammen mit der Kerr-NUT-Metrik ) axialsymmetrisch ist, kann sie in eine Form gebracht werden, auf die die Belinski-Zakharov-Transformation angewendet werden kann. Dies impliziert, dass das Schwarze Loch von Kerr die Form eines gravitativen Solitons hat .

Masse der Rotationsenergie

Entzieht man einem Schwarzen Loch die komplette Rotationsenergie , zum Beispiel mit dem Penrose-Prozess , kann die verbleibende Masse nicht unter die irreduzible Masse schrumpfen. Wenn also ein Schwarzes Loch mit dem Spin rotiert , ist sein Gesamtmassenäquivalent um den Faktor höher im Vergleich zu einem entsprechenden Schwarzschild-Schwarzen Loch mit gleich . Der Grund dafür ist, dass, um einen statischen Körper zum Drehen zu bringen, Energie auf das System aufgebracht werden muss. Wegen der Masse-Energie-Äquivalenz hat diese Energie auch ein Masse-Äquivalent, das sich zur Gesamtmasse-Energie des Systems addiert, . ${\displaystyle E_{\rm {rot}}=c^{2}\left(M-M_{\rm {irr}}\right)}$${\displaystyle a=M}$${\displaystyle M}$${\displaystyle {\sqrt {2}}}$${\displaystyle M}$${\displaystyle M_{\rm {irr}}}$${\displaystyle M}$

Das gesamte Massenäquivalent (die gravitierende Masse) des Körpers (einschließlich seiner Rotationsenergie ) und seine irreduzible Masse stehen in Beziehung zu ${\displaystyle M}$${\displaystyle M_{\rm {irr}}}$

${\displaystyle 2M_{\rm {irr}}^{2}=M^{2}+{\sqrt {M^{4}-J^{2}c^{2}/G^{2}}} \Longrightarrow M^{2}={\frac {4M_{\rm {irr}}^{4}}{4M_{\rm {irr}}^{2}-a^{2}c^{4}/ G^{2}}}.}$

Wellenoperator

Da selbst eine direkte Überprüfung der Kerr-Metrik umständliche Rechnungen erfordert, sind die kontravarianten Komponenten des Metriktensors in Boyer-Lindquist-Koordinaten im Ausdruck für das Quadrat des Vier-Gradienten- Operators unten dargestellt : ${\displaystyle g^{ik}}$

${\displaystyle g^{\mu\nu }{\frac {\partial }{\partial x^{\mu}}}{\frac {\partial}{\partial x^{\nu}}}=-{ \frac {1}{c^{2}\Delta}}\left(r^{2}+a^{2}+{\frac {r_{s}ra^{2}}{\Sigma}}\ sin ^{2}\theta \right)\left({\frac {\partial }{\partial t}}\right)^{2}-{\frac {2r_{s}ra}{c\Sigma\Delta }}{\frac{\partial}{\partial\phi}}{\frac{\partial}{\partial{t}}}+{\frac{1}{\Updelta\sin^{2}\theta} }\left(1-{\frac{r_{s}r}{\Sigma}}\right)\left({\frac{\partial }{\partial\phi}}\right)^{2}+{ \frac {\Delta }{\Sigma}}\left({\frac {\partial }{\partial r}}\right)^{2}+{\frac {1}{\Sigma}}\left({ \frac {\partial }{\partial \theta }}\right)^{2}}$

( 15 )

Rahmen ziehen

Wir können die Kerr-Metrik ( 1 ) in der folgenden Form umschreiben :

${\displaystyle c^{2}d\tau^{2}=\left(g_{tt}-{\frac {g_{t\phi}^{2}}{g_{\phi\phi}}}\ rechts)dt^{2}+g_{rr}dr^{2}+g_{\theta\theta}d\theta^{2}+g_{\phi\phi}\left(d\phi +{\frac {g_{t\phi}}{g_{\phi\phi}}}dt\right)^{2}.}$

( 16 )

Diese Metrik entspricht einem mitrotierenden Referenzsystem, das sich mit der Winkelgeschwindigkeit Ω dreht, die sowohl vom Radius r als auch vom Kolatitude θ abhängt , wobei Ω Killing-Horizont genannt wird .

${\displaystyle \Omega =-{\frac {g_{t\phi}}{g_{\phi\phi}}}={\frac {r_{s}rac}{\Sigma \left(r^{2} +a^{2}\right)+r_{s}ra^{2}\sin^{2}\theta}}.}$

( 17 )

Somit wird ein Trägheitsbezugssystem von der rotierenden Zentralmasse mitgenommen, um an deren Rotation teilzunehmen; dies wird als Frame-Dragging bezeichnet und wurde experimentell getestet. Qualitativ kann Frame-Dragging als das Gravitationsanalogon der elektromagnetischen Induktion angesehen werden. Eine "Eisläuferin", die sich in einer Umlaufbahn über dem Äquator befindet und in Bezug auf die Sterne rotierend ruht, streckt ihre Arme aus. Der Arm, der in Richtung des Schwarzen Lochs ausgestreckt ist, wird drehwärts verdreht. Der vom Schwarzen Loch weggestreckte Arm wird gegen die Drehung verdreht. Sie wird daher im Gegensinn zum Schwarzen Loch rotatorisch beschleunigt. Dies ist das Gegenteil von dem, was in der alltäglichen Erfahrung passiert. Wenn sie sich bereits mit einer bestimmten Geschwindigkeit dreht, wenn sie ihre Arme ausstreckt, gleichen sich Trägheitseffekte und Frame-Draging-Effekte aus und ihre Drehung ändert sich nicht. Aufgrund des Äquivalenzprinzips sind Gravitationseffekte lokal nicht von Trägheitseffekten zu unterscheiden, daher ist diese Rotationsrate, bei der beim Ausstrecken der Arme nichts passiert, ihre lokale Referenz für die Nichtrotation. Dieser Rahmen dreht sich in Bezug auf die Fixsterne und dreht sich in Bezug auf das Schwarze Loch gegenläufig. Eine nützliche Metapher ist ein Planetengetriebesystem , bei dem das Schwarze Loch das Sonnenrad ist, der Eisläufer ein Planetengetriebe und das äußere Universum das Hohlrad. Dies kann auch durch das Mach-Prinzip interpretiert werden .

Wichtige Oberflächen

Lage der Horizonte, Ergosphären und der Ringsingularität der Kerr-Raumzeit in kartesischen Kerr-Schild-Koordinaten.

Vergleich des Schattens (schwarz) und der wichtigen Oberflächen (weiß) eines Schwarzen Lochs. Der Spinparameter a wird von 0 bis M animiert , während sich die linke Seite des Schwarzen Lochs zum Beobachter hin dreht.

Die Kerr-Metrik ( 1 ) hat zwei physikalisch relevante Oberflächen, auf denen sie singulär erscheint. Die innere Oberfläche entspricht einem Ereignishorizont ähnlich dem in der Schwarzschild-Metrik beobachteten ; dies tritt dort auf, wo die rein radiale Komponente g _rr der Metrik gegen Unendlich geht. Das Lösen der quadratischen Gleichung 1 ⁄ g _rr  = 0 liefert die Lösung:

${\displaystyle r_{\rm {H}}^{\pm}={\frac {r_{s}\pm {\sqrt {r_{s}^{2}-4a^{2}}}}{2 }}}$

was in natürlichen Einheiten (die G  =  M  =  c  = 1 ergeben) vereinfacht zu:

${\displaystyle r_{\rm {H}}^{\pm}=1\pm {\sqrt {1-a^{2}}}}$

Eine weitere scheinbare Singularität tritt auf, wenn die rein zeitliche Komponente g _tt der Metrik das Vorzeichen von positiv nach negativ ändert. Das Lösen einer quadratischen Gleichung g _tt  = 0 ergibt wiederum die Lösung:

${\displaystyle r_{\rm {E}}^{\pm}={\frac {r_{s}\pm {\sqrt {r_{s}^{2}-4a^{2}\cos ^{2 }\theta }}}{2}}}$

oder in natürlichen Einheiten:

${\displaystyle r_{\rm {E}}^{\pm}=1\pm {\sqrt {1-a^{2}\cos^{2}\theta}}}$

Aufgrund des cos ² θ- Terms in der Quadratwurzel ähnelt diese Außenfläche einer abgeflachten Kugel, die die Innenfläche an den Polen der Rotationsachse berührt, wobei der Kolatitude θ gleich 0 oder π ist ; der raum zwischen diesen beiden flächen wird ergosphäre genannt . Innerhalb dieses Volumens ist die rein zeitliche Komponente g _tt negativ, dh wirkt wie eine rein räumliche metrische Komponente. Folglich müssen Teilchen innerhalb dieser Ergosphäre mit der inneren Masse mitrotieren, wenn sie ihren zeitähnlichen Charakter behalten sollen. Ein sich bewegendes Teilchen erfährt eine positive Eigenzeit entlang seiner Weltlinie , seinem Weg durch die Raumzeit . Dies ist jedoch innerhalb der Ergosphäre, wo g _tt negativ ist, nicht möglich, es sei denn, das Teilchen rotiert mit der inneren Masse M mit einer Winkelgeschwindigkeit von mindestens Ω . Somit kann innerhalb der Ergosphäre kein Teilchen entgegengesetzt zur Zentralmasse rotieren.

Wie beim Ereignishorizont in der Schwarzschild-Metrik sind die scheinbaren Singularitäten bei r _H und r _E Illusionen, die durch die Wahl der Koordinaten erzeugt werden (dh sie sind Koordinatensingularitäten ). Tatsächlich kann die Raumzeit durch sie durch eine geeignete Wahl der Koordinaten glatt fortgeführt werden.

Ergosphäre und das Penrose-Verfahren

Ein Schwarzes Loch ist im Allgemeinen von einer Oberfläche umgeben, die als Ereignishorizont bezeichnet wird und sich auf dem Schwarzschild-Radius für ein nicht rotierendes Schwarzes Loch befindet, wobei die Fluchtgeschwindigkeit gleich der Lichtgeschwindigkeit ist. Innerhalb dieser Oberfläche kann sich kein Beobachter/Teilchen auf einem konstanten Radius halten. Es ist gezwungen, nach innen zu fallen, was manchmal als statische Grenze bezeichnet wird .

Ein rotierendes Schwarzes Loch hat die gleiche statische Grenze an seinem Ereignishorizont, aber es gibt eine zusätzliche Oberfläche außerhalb des Ereignishorizonts, die als "Ergooberfläche" bezeichnet wird

${\displaystyle (rM)^{2}=M^{2}-J^{2}\cos^{2}\theta}$

in Boyer-Lindquist-Koordinaten , die intuitiv als die Kugel charakterisiert werden können, in der "die Rotationsgeschwindigkeit des umgebenden Raums" mit der Lichtgeschwindigkeit mitgezogen wird. Innerhalb dieser Sphäre ist das Ziehen größer als die Lichtgeschwindigkeit und jeder Beobachter/Teilchen wird gezwungen, sich mitzurotieren.

Der Bereich außerhalb des Ereignishorizontes , sondern innerhalb der Oberfläche , wo die Rotationsgeschwindigkeit die Lichtgeschwindigkeit ist, wird das genannt ERGOSPHERE (aus dem Griechischen ergon Bedeutung der Arbeit ). Partikel, die in die Ergosphäre fallen, werden gezwungen, schneller zu rotieren und gewinnen dadurch Energie. Da sie sich noch außerhalb des Ereignishorizonts befinden, können sie dem Schwarzen Loch entkommen. Der Nettoprozess besteht darin, dass das rotierende Schwarze Loch auf Kosten seiner eigenen Gesamtenergie energiereiche Teilchen emittiert. Die Möglichkeit, einem rotierenden Schwarzen Loch Spinenergie zu entziehen, wurde erstmals 1969 von dem Mathematiker Roger Penrose vorgeschlagen und wird deshalb als Penrose-Prozess bezeichnet . Rotierende Schwarze Löcher in der Astrophysik sind eine potenzielle Quelle großer Energiemengen und werden verwendet, um energetische Phänomene wie Gammastrahlenausbrüche zu erklären .

Merkmale der Kerr-Geometrie

Die Kerr-Geometrie weist viele bemerkenswerte Merkmale auf: Die maximale analytische Erweiterung umfasst eine Folge asymptotisch flacher Außenbereiche, die jeweils einer Ergosphäre zugeordnet sind , stationäre Grenzflächen, Ereignishorizonte , Cauchy-Horizonte , geschlossene zeitähnliche Kurven und eine ringförmige Krümmungssingularität . Die geodätische Gleichung kann in geschlossener Form exakt gelöst werden. Neben zwei Killing-Vektorfeld (entsprechend Zeit Übersetzung und Axialsymmetrie ) räumt die Kerr - Geometrie eine bemerkenswerte Abtöten Tensor . Es gibt ein Paar von prinzipiellen Nullkongruenzen (eine eingehende und eine ausgehende ). Die Weyl - Tensor ist algebraisch besondere , in der Tat hat es Petrov Typ D . Die globale Struktur ist bekannt. Topologisch lässt sich der Homotopietyp der Kerr-Raumzeit einfach als Linie mit Kreisen an jedem ganzzahligen Punkt charakterisieren.

Beachten Sie, dass die innere Kerr-Geometrie in Bezug auf Störungen im Innenbereich instabil ist. Diese Instabilität bedeutet, dass, obwohl die Kerr-Metrik achsensymmetrisch ist, ein Schwarzes Loch, das durch Gravitationskollaps entstanden ist, dies möglicherweise nicht ist. Diese Instabilität impliziert auch, dass viele der oben beschriebenen Merkmale der Kerr-Geometrie innerhalb eines solchen Schwarzen Lochs möglicherweise nicht vorhanden sind.

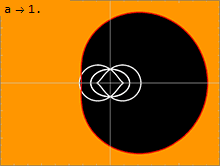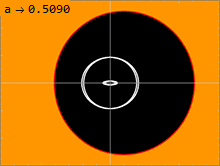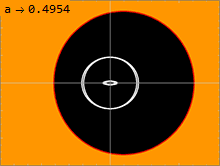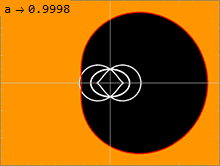
Eine Oberfläche, auf der Licht ein Schwarzes Loch umkreisen kann, wird Photonenkugel genannt. Die Kerr-Lösung hat unendlich viele Photonenkugeln , die zwischen einer inneren und einer äußeren liegen. Bei der nicht rotierenden Schwarzschild-Lösung mit a = 0 entarten die innere und die äußere Photonenkugel, so dass es nur eine Photonenkugel auf einem einzigen Radius gibt. Je größer der Spin eines Schwarzen Lochs ist, desto weiter entfernen sich die innere und die äußere Photonenkugel. Ein Lichtstrahl, der sich in eine dem Spin des Schwarzen Lochs entgegengesetzte Richtung ausbreitet, wird das Loch an der äußeren Photonenkugel kreisförmig umkreisen. Ein Lichtstrahl, der in die gleiche Richtung wie der Spin des Schwarzen Lochs wandert, wird kreisförmig um die innere Photonenkugel kreisen. Umlaufende Geodäten mit einem gewissen Drehimpuls senkrecht zur Rotationsachse des Schwarzen Lochs kreisen auf Photonenkugeln zwischen diesen beiden Extremen. Da die Raumzeit rotiert, zeigen solche Bahnen eine Präzession, da sich die Variable nach Ablauf einer Periode in der Variablen verschiebt. ${\displaystyle \phi\,}$${\displaystyle\theta\,}$

Bahngleichungen

Animation der Umlaufbahn eines Testteilchens um ein sich drehendes Schwarzes Loch. Links: Draufsicht, rechts: Seitenansicht.

Eine weitere Flugbahn einer Testmasse um ein sich drehendes (Kerr) Schwarzes Loch. Im Gegensatz zu Umlaufbahnen um ein Schwarzes Schwarzschild-Loch ist die Umlaufbahn nicht auf eine einzelne Ebene beschränkt, sondern füllt eine torusähnliche Region um den Äquator ergodisch aus .

Die Bewegungsgleichungen für Testteilchen in der Kerr-Raumzeit werden von vier Bewegungskonstanten bestimmt . Die erste ist die unveränderliche Masse des Testteilchens, definiert durch die Beziehung ${\displaystyle\mu}$

${\displaystyle -\mu^{2}=p^{\alpha}g_{\alpha\beta}p^{\beta},}$

wo ist der Viererimpuls des Teilchens. Darüber hinaus gibt es zwei Bewegungskonstanten, die durch die Zeitverschiebungs- und Rotationssymmetrien der Kerr-Raumzeit gegeben sind, die Energie und die Komponente des Bahndrehimpulses parallel zum Spin des Schwarzen Lochs . ${\displaystyle p^{\alpha}}$${\displaystyle E}$${\displaystyle L_{z}}$

${\displaystyle E=-p_{t}}$, und

${\displaystyle L_{z}=p_{\phi}}$

Mit der Hamilton-Jacobi-Theorie zeigte Brandon Carter , dass es eine vierte Bewegungskonstante gibt , die jetzt als Carter-Konstante bezeichnet wird . Sie hängt mit dem Gesamtdrehimpuls des Teilchens zusammen und ist gegeben durch ${\displaystyle Q}$

${\displaystyle Q=p_{\theta}^{2}+\cos^{2}\theta\left(a^{2}\left(\mu^{2}-E^{2}\right)+ \left({\frac{L_{z}}{\sin\theta}}\right)^{2}\right)}$.

Da es vier (unabhängige) Bewegungskonstanten für Freiheitsgrade gibt, sind die Bewegungsgleichungen für ein Testteilchen in der Kerr-Raumzeit integrierbar .

Unter Verwendung dieser Bewegungskonstanten können die Bahngleichungen für ein Testteilchen geschrieben werden (unter Verwendung der natürlichen Einheiten von G = M = c = 1),

${\displaystyle {\begin{ausgerichtet}\Sigma {\frac {dr}{d\lambda}}&=\pm {\sqrt {R(r)}}\\\Sigma {\frac {d\theta }{ d\lambda }}&=\pm {\sqrt {\Theta (\theta )}}\\\Sigma {\frac {d\phi }{d\lambda }}&=-\left(aE-{\frac {L_{z}}{\sin^{2}\theta}}\right)+{\frac {a}{\Delta}}P(r)\\\Sigma {\frac {dt}{d\lambda }}&=-a\left(aE\sin^{2}\theta -L_{z}\right)+{\frac {r^{2}+a^{2}}{\Delta }}P( r)\end{ausgerichtet}}}$

mit

${\displaystyle \Theta(\theta)=Q-\cos^{2}\theta\left(a^{2}\left(\mu^{2}-E^{2}\right)+{\frac {L_{z}^{2}}{\sin^{2}\theta}}\right)}$

${\displaystyle P(r)=E\left(r^{2}+a^{2}\right)-aL_{z}}$

${\displaystyle R(r)=P(r)^{2}-\Delta\left(\mu^{2}r^{2}+(L_{z}-aE)^{2}+Q\right )}$

Wo ist ein affiner Parameter, so dass . Insbesondere wenn der affine Parameter auf die richtige Zeit bis bezogen ist . ${\displaystyle \lambda}$${\displaystyle {\frac {dx^{\alpha}}{d\lambda}}=p^{\alpha}}$${\displaystyle \mu >0}$${\displaystyle \lambda}$${\displaystyle \tau}$${\displaystyle \lambda =\tau /\mu}$

Aufgrund des Frame-Dragging- Effekts rotiert ein Null-Winkel-Impuls-Beobachter (ZAMO) mit der Winkelgeschwindigkeit, die in Bezug auf die Koordinatenzeit des Buchhalters definiert ist . Die lokale Geschwindigkeit des Testteilchens wird relativ zu einer mit rotierenden Sonde gemessen . Die gravitative Zeitdilatation zwischen einem ZAMO bei festem und einem stationären Beobachter weit entfernt von der Masse beträgt ${\displaystyle \Omega}$${\displaystyle t}$${\displaystyle v}$${\displaystyle \Omega}$${\displaystyle r}$

${\displaystyle {\frac {t}{\tau}}={\sqrt {\frac {\left(a^{2}+r^{2}\right)^{2}-a^{2}\ Delta \sin^{2}\theta }{\Delta\\Sigma}}}}$.

Symmetrien

Die Isometriegruppe der Kerr-Metrik ist die Untergruppe der zehndimensionalen Poincaré-Gruppe, die den zweidimensionalen Ort der Singularität zu sich nimmt. Es behält die zeitlichen Translationen (eindimensional) und Rotationen um seine Rotationsachse (eindimensional) bei. Es hat also zwei Dimensionen. Wie die Poincaré-Gruppe hat sie vier miteinander verbundene Komponenten: die Komponente der Identität; die Komponente, die Zeit und Länge umkehrt; die Komponente, die durch die Äquatorialebene reflektiert wird; und die Komponente, die beides kann.

In der Physik sind Symmetrien typischerweise mit erhaltenen Bewegungskonstanten in Übereinstimmung mit dem Noether-Theorem verbunden . Wie oben gezeigt, haben die geodätischen Gleichungen vier Erhaltungsgrößen: Eine davon stammt aus der Definition einer Geodäte und zwei davon resultieren aus der Zeittranslation und Rotationssymmetrie der Kerr-Geometrie. Die vierte Erhaltungsgröße ergibt sich nicht aus einer Symmetrie im üblichen Sinne und wird allgemein als versteckte Symmetrie bezeichnet.

Überextreme Kerr-Lösungen

Die Lage des Ereignishorizonts wird durch die größere Wurzel von bestimmt . Wenn (dh ) es keine (real bewerteten) Lösungen für diese Gleichung gibt und es keinen Ereignishorizont gibt. Ohne Ereignishorizonte, die es vor dem Rest des Universums verbergen, hört das Schwarze Loch auf, ein Schwarzes Loch zu sein, und wird stattdessen eine nackte Singularität sein . ${\displaystyle \Delta =0}$${\displaystyle r_{s}/2<a}$${\displaystyle GM^{2}<Jc}$

Kerr Schwarze Löcher als Wurmlöcher

Obwohl die Kerr-Lösung an den Wurzeln von Δ = 0 singulär zu sein scheint, sind dies tatsächlich Koordinatensingularitäten , und mit einer geeigneten Wahl neuer Koordinaten kann die Kerr-Lösung glatt um die diesen Wurzeln entsprechenden Werte von erweitert werden . Die größere dieser Wurzeln bestimmt die Lage des Ereignishorizonts und die kleinere die Lage eines Cauchy-Horizonts. Eine (zukunftsgerichtete, zeitähnliche) Kurve kann im Äußeren beginnen und durch den Ereignishorizont gehen. Nach dem Durchlaufen des Ereignishorizonts verhält sich die Koordinate nun wie eine Zeitkoordinate, muss also abnehmen, bis die Kurve den Cauchy-Horizont passiert. ${\displaystyle r}$${\displaystyle r}$

Die Region jenseits des Cauchy-Horizonts weist einige überraschende Merkmale auf. Die Koordinate verhält sich wiederum wie eine Raumkoordinate und kann frei variieren. Der Innenbereich hat eine Reflexionssymmetrie, so dass sich eine (zukunftsgerichtete zeitähnliche) Kurve entlang eines symmetrischen Pfades fortsetzen kann, der sich durch einen zweiten Cauchy-Horizont, durch einen zweiten Ereignishorizont und hinaus in einen neuen Außenbereich fortsetzt, der isometrisch zum ursprünglichen Außenbereich der Kerr-Lösung. Die Kurve könnte dann in der neuen Region ins Unendliche entweichen oder in den zukünftigen Ereignishorizont der neuen äußeren Region eintreten und den Vorgang wiederholen. Dieses zweite Äußere wird manchmal als ein anderes Universum betrachtet. Andererseits ist in der Kerr-Lösung die Singularität ein Ring , und die Kurve kann durch das Zentrum dieses Rings verlaufen. Der Bereich darüber hinaus erlaubt geschlossene zeitähnliche Kurven. Da die Flugbahn von Beobachtern und Teilchen in der Allgemeinen Relativitätstheorie durch zeitähnliche Kurven beschrieben wird, ist es für Beobachter in dieser Region möglich, in ihre Vergangenheit zurückzukehren. Diese innere Lösung ist wahrscheinlich nicht physikalisch und wird als rein mathematisches Artefakt betrachtet. ${\displaystyle r}$

Während erwartet wird, dass der äußere Bereich der Kerr-Lösung stabil ist und sich alle rotierenden Schwarzen Löcher schließlich einer Kerr-Metrik nähern, scheint der innere Bereich der Lösung instabil zu sein, ähnlich wie ein Bleistift, der auf seiner Spitze balanciert. Dies hängt mit der Idee der kosmischen Zensur zusammen .

Beziehung zu anderen exakten Lösungen

Die Kerr-Geometrie ist ein besonderes Beispiel für eine stationäre axialsymmetrische Vakuumlösung der Einstein-Feldgleichung . Die Familie aller stationären achsensymmetrischen Vakuumlösungen der Einsteinschen Feldgleichung sind die Ernst-Vakuum .

Die Kerr-Lösung bezieht sich auch auf verschiedene Nicht-Vakuum-Lösungen, die Schwarze Löcher modellieren. Zum Beispiel modelliert das Kerr-Newman-Elektrovakuum ein (rotierendes) Schwarzes Loch, das mit einer elektrischen Ladung ausgestattet ist, während das Kerr-Vaidya- Nullstaub ein (rotierendes) Loch mit einfallender elektromagnetischer Strahlung modelliert.

Der Spezialfall der Kerr-Metrik ergibt die Schwarzschild-Metrik , die ein nicht rotierendes Schwarzes Loch, das statisch und kugelsymmetrisch ist , in den Schwarzschild-Koordinaten modelliert . (In diesem Fall verschwindet jeder Geroch-Moment außer der Masse.) ${\displaystyle a=0}$

Das Innere der Kerr-Geometrie, oder eher ein Teil davon, ist lokal isometrisch zum Chandrasekhar-Ferrari CPW-Vakuum , einem Beispiel für ein kollidierendes ebenes Wellenmodell . Dies ist besonders interessant, da sich die globale Struktur dieser CPW-Lösung stark von der der Kerr-Geometrie unterscheidet und ein Experimentator im Prinzip hoffen könnte, die Geometrie (des äußeren Teils) des Kerr-Innenraums durch Anordnung der Kollision von zwei geeignete ebene Gravitationswellen .

Multipolmomente

Jedes asymptotisch flache Ernst-Vakuum kann durch die unendliche Folge relativistischer Multipolmomente charakterisiert werden, von denen die ersten beiden als Masse und Drehimpuls der Feldquelle interpretiert werden können . Es gibt alternative Formulierungen relativistischer Multipolmomente nach Hansen, Thorne und Geroch, die sich als übereinstimmend herausstellen. Die relativistischen Multipolmomente der Kerr-Geometrie wurden von Hansen berechnet; sie stellen sich als heraus

${\displaystyle M_{n}=M[ia]^{n}}$

Somit  ergibt der Spezialfall des Schwarzschild-Vakuums ( a = 0) die „Monopol- Punktquelle “ der Allgemeinen Relativitätstheorie.

Weyl-Multipolmomente entstehen durch die Behandlung einer bestimmten metrischen Funktion (formal entsprechend dem Newtonschen Gravitationspotential), die das Weyl-Papapetrou-Diagramm für die Ernst-Familie aller stationären achsensymmetrischen Vakuumlösungen unter Verwendung der standardmäßigen euklidischen skalaren Multipolmomente erscheint . Sie unterscheiden sich von den oben von Hansen berechneten Momenten. In gewisser Weise charakterisieren die Weyl-Momente nur (indirekt) die "Massenverteilung" einer isolierten Quelle, und sie hängen nur von den relativistischen Momenten gerader Ordnung ab . Bei quer zur Äquatorebene symmetrischen Lösungen verschwinden die Weyl-Momente ungerader Ordnung . Für die Kerr-Vakuumlösungen sind die ersten Weyl-Momente gegeben durch

${\displaystyle a_{0}=M,\qquad a_{1}=0,\qquad a_{2}=M\left({\frac {M^{2}}{3}}-a^{2} \rechts)}$

Insbesondere sehen wir, dass das Schwarzschild-Vakuum ein Weyl-Moment zweiter Ordnung ungleich null hat, entsprechend der Tatsache, dass der "Weyl-Monopol" die Chazy-Curzon-Vakuumlösung ist, nicht die Schwarzschild-Vakuumlösung, die aus dem Newtonschen Potential einer bestimmten endlichen Länge gleichmäßige Dichte dünner Stab .

In der Allgemeinen Relativitätstheorie mit schwachem Feld ist es zweckmäßig, isolierte Quellen mit einer anderen Art von Multipol zu behandeln, die die Weyl-Momente zu Massen-Multipolmomenten und Impuls-Multipolmomenten verallgemeinert , die jeweils die Verteilung der Masse und des Impulses der Quelle charakterisieren . Dabei handelt es sich um mehrfach indizierte Größen, deren geeignet symmetrisierte und antisymmetrisierte Teile sich auf ziemlich komplizierte Weise mit den Real- und Imaginärteilen der relativistischen Momente für die vollständige nichtlineare Theorie in Beziehung setzen lassen.

Perez und Moreschi haben einen alternativen Begriff von "Monopollösungen" gegeben, indem sie die Standard-NP-Tetrade der Ernst-Vakuums in Potenzen von r (der radialen Koordinate in der Weyl-Papapetrou-Karte) erweitert haben. Nach dieser Formulierung:

• die isolierte Masse monopole Quelle mit Nulldrehimpuls ist die Schwarzschild- Vakuum Familie (ein Parameter),
• die isolierte Massemonopolquelle mit radialem Drehimpuls ist die Taub-NUT-Vakuumfamilie (zwei Parameter; nicht ganz asymptotisch flach),
• die isolierte Massemonopolquelle mit axialem Drehimpuls ist die Kerr-Vakuumfamilie (zwei Parameter).

In diesem Sinne sind die Kerr-Vakuum die einfachsten stationären achsensymmetrischen asymptotisch flachen Vakuumlösungen in der Allgemeinen Relativitätstheorie.

Offene Probleme

Die Kerr-Geometrie wird oft als Modell eines rotierenden Schwarzen Lochs verwendet . Aber wenn wir davon ausgehen, dass die Lösung nur außerhalb eines kompakten Bereichs gültig ist (vorbehaltlich bestimmter Einschränkungen), sollten wir sie im Prinzip als äußere Lösung verwenden können , um das Gravitationsfeld um ein rotierendes massereiches Objekt, das kein Schwarzes Loch ist, zu modellieren, wie ein Neutronenstern oder die Erde. Dies funktioniert sehr gut für den nicht rotierenden Fall, in dem wir das Äußere des Schwarzschild-Vakuums einem Schwarzschild-Fluidinneren und tatsächlich allgemeineren statischen kugelsymmetrischen perfekten Fluidlösungen zuordnen können. Das Problem, ein rotierendes perfekt fluides Inneres zu finden, das an ein Kerr-Äußeres oder tatsächlich an jede asymptotisch flache Vakuum-Außenlösung angepasst werden kann, hat sich jedoch als sehr schwierig erwiesen. Insbesondere die Wahlquist-Flüssigkeit , die einst als Kandidat für die Anpassung an ein Kerr-Exterieur angesehen wurde, ist heute dafür bekannt, eine solche Anpassung nicht zuzulassen. Derzeit scheint es, dass nur Näherungslösungen bekannt sind, die langsam rotierende Flüssigkeitskugeln modellieren. (Dies sind das relativistische Analogon abgeflachter (fetter, gedrungener) kugelförmiger Kugeln mit Masse und Drehimpuls ungleich Null, aber verschwindenden höheren Multipolmomenten.) Das Äußere der Neugebauer-Meinel-Scheibe , eine exakte Staublösung, die eine rotierende dünne Scheibe modelliert, nähert sich im Grenzfall der Kerr-Geometrie. Es sind auch physikalische Thin-Disk-Lösungen bekannt, die durch die Identifizierung von Teilen der Kerr-Raumzeit erhalten werden. ${\displaystyle GM^{2}=cJ}$

Siehe auch

• Schwarzschild-Metrik
• Kerr-Newman-Metrik
• Reissner-Nordström-Metrik
• Spin-Flip
• Kerr-Schild-Raumzeit
• Rotierendes Schwarzes Loch

Fußnoten

Verweise

Weiterlesen

• Wiltshire, David L.; Visser, Matt; Scott, Susan M. , Hrsg. (2009). Die Kerr-Raumzeit: Rotierende Schwarze Löcher in der Allgemeinen Relativitätstheorie . Cambridge: Cambridge University Press. ISBN 978-0-521-88512-6.
• Stephani, Hans; Kramer, Dietrich; MacCallum, Malcolm; Hoenselaers, Cornelius; Herlt, Eduard (2003). Exakte Lösungen der Einsteinschen Feldgleichungen . Cambridge: Cambridge University Press. ISBN 978-0-521-46136-8.
• Meinel, Reinhard ; Ansorg, Marcus; Kleinwächter, Andreas; Neugebauer, Gernot; Petroff, David (2008). Relativistische Gleichgewichtszahlen . Cambridge: Cambridge University Press. ISBN 978-0-521-86383-4.
• O'Neill, Barrett (1995). Die Geometrie der Schwarzen Löcher von Kerr . Wellesley, Massachusetts: AK Peters. ISBN 978-1-56881-019-5.
• D'Inverno, Ray (1992). Einführung in Einsteins Relativitätstheorie . Oxford: Clarendon Press. ISBN 978-0-19-859686-8. Siehe Kapitel 19 für eine lesbare Einführung in das fortgeschrittene Grundstudium.
• Chandrasekhar, S. (1992). Die mathematische Theorie der Schwarzen Löcher . Oxford: Clarendon Press. ISBN 978-0-19-850370-5. Siehe Kapitel 6 bis 10 für eine sehr gründliche Studie auf fortgeschrittenem Niveau.
• Griffiths, JB (1991). Kollidierende ebene Wellen in der Allgemeinen Relativitätstheorie . Oxford: Oxford University Press. ISBN 978-0-19-853209-5. Siehe Kapitel 13 für das Chandrasekhar/Ferrari CPW-Modell.
• Adler, Ronald; Bazin, Maurice; Schiffer, Menahem (1975). Einführung in die Allgemeine Relativitätstheorie (Zweite Aufl.). New York: McGraw-Hill. ISBN 978-0-07-000423-8. Siehe Kapitel 7 .
• Penrose, R. (1968). Hrsg. C. de Witt und J. Wheeler (Hrsg.). Battelle Rencontres . WA Benjamin, New York. P. 222.
• Perez, Alejandro; Moreschi, Osvaldo M. (2000). „Charakterisierung exakter Lösungen aus asymptotischen physikalischen Konzepten“. arXiv : gr-qc/0012100v1 . Charakterisierung von drei Standardfamilien von Vakuumlösungen wie oben erwähnt.
• Sotiriou, Thomas P.; Apostolatos, Theocharis A. (2004). „Korrekturen und Kommentare zu den Multipolmomenten achsensymmetrischer Elektrovakuum-Raumzeiten“. Klasse. Quantengrav . 21 (24): 5727–5733. arXiv : gr-qc/0407064 . Bibcode : 2004CQGra..21.5727S . doi : 10.1088/0264-9381/21/24/003 . S2CID  16858122 . Gibt die relativistischen Multipolmomente für das Ernst-Vakuum (plus die elektromagnetischen und gravitativ-relativistischen Multipolmomente für die geladene Verallgemeinerung) an.
• Carter, B. (1971). "Achsensymmetrisches Schwarzes Loch hat nur zwei Freiheitsgrade". Physische Überprüfungsbriefe . 26 (6): 331–333. Bibcode : 1971PhRvL..26..331C . doi : 10.1103/PhysRevLett.26.331 .
• Wald, RM (1984). Allgemeine Relativitätstheorie . Chicago: Die University of Chicago Press. S. 312–324. ISBN 978-0-226-87032-8.
• Kerr, RP; Schild, A. (2009). „Republication of: Eine neue Klasse von Vakuumlösungen der Einstein-Feldgleichungen“. Allgemeine Relativitätstheorie und Gravitation . 41 (10): 2485–2499. Bibcode : 2009GReGr..41.2485K . doi : 10.1007/s10714-009-0857-z . S2CID  361088 .
• Krasiński, Andrzej; Verdaguer, Enric; Kerr, Roy Patrick (2009). "Redaktionelle Anmerkung an: RP Kerr und A. Schild, Eine neue Klasse von Vakuumlösungen der Einstein-Feldgleichungen" . Allgemeine Relativitätstheorie und Gravitation . 41 (10): 2469–2484. Bibcode : 2009GReGr..41.2469K . doi : 10.1007/s10714-009-0856-0 . "... Diese Notiz ist als Leitfaden für diejenigen Leser gedacht, die alle Details [der Herleitung der Kerr-Lösung] überprüfen möchten..."