Richtungsableitung - Directional derivative

In der Mathematik repräsentiert die Richtungsableitung einer multivariaten differenzierbaren (skalaren) Funktion entlang eines gegebenen Vektors v an einem gegebenen Punkt x intuitiv die momentane Änderungsrate der Funktion, die sich mit einer durch v spezifizierten Geschwindigkeit durch x bewegt .

Die Richtungsableitung einer Skalarfunktion f in Bezug auf einen Vektor v an einem Punkt (z. B. Position) x kann wie folgt bezeichnet werden:

\nabla _{\mathbf {v} }{f}(\mathbf {x} )=f'_{\mathbf {v} }(\mathbf {x} )=D_{\mathbf {v} } f(\mathbf{x})=Df(\mathbf{x})(\mathbf{v})=\partial_{\mathbf{v}}f(\mathbf{x})=\mathbf{v}\ cdot {\nabla f(\mathbf {x} )}=\mathbf {v} \cdot {\frac {\partial f(\mathbf {x})}{\partial\mathbf {x}}}

.

Es verallgemeinert daher den Begriff einer partiellen Ableitung , bei der die Änderungsrate entlang einer der krummlinigen Koordinatenkurven genommen wird, während alle anderen Koordinaten konstant sind. Die Richtungsableitung ist ein Spezialfall der Gateaux-Ableitung .

Definition

Ein Konturdiagramm von , das den Gradientenvektor in Schwarz und den Einheitsvektor skaliert durch die Richtungsableitung in Richtung von in Orange zeigt. Der Gradientenvektor ist länger, weil der Gradient in Richtung der größten Anstiegsrate einer Funktion zeigt.

f(x,y)=x^{2}+y^{2}

{\displaystyle\mathbf{u}}

{\displaystyle\mathbf{u}}

Die Richtungsableitung einer Skalarfunktion

f(\mathbf{x})=f(x_{1},x_{2},\ldots,x_{n})

entlang eines Vektors

\mathbf{v} =(v_{1},\ldots,v_{n})

ist die durch den Grenzwert definierte Funktion $\nabla_{\mathbf {v} }{f}$

\nabla _{\mathbf {v} }{f}(\mathbf {x} )=\lim _{h\to 0}{\frac {f(\mathbf {x} +h\mathbf {v } )-f(\mathbf{x})}{h}}.

Diese Definition ist in einem breiten Bereich von Kontexten gültig, beispielsweise wenn die Norm eines Vektors (und damit eines Einheitsvektors) undefiniert ist.

Für differenzierbare Funktionen

Wenn die Funktion f ist differenzierbar in x , so wird die Richtungsableitung existiert entlang eines beliebigen Vektors v , und man hat

\nabla _{\mathbf {v} }{f}(\mathbf {x} )=\nabla f(\mathbf {x} )\cdot \mathbf {v}

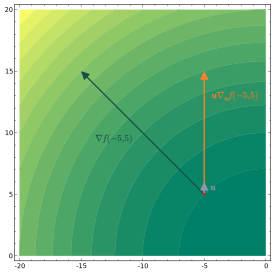
wobei das rechte die Steigung bezeichnet und das Punktprodukt ist . Dies folgt aus der Definition eines Pfades und der Verwendung der Definition der Ableitung als Grenzwert, der entlang dieses Pfads berechnet werden kann, um zu erhalten: ${\displaystyle\nabla}$ ${\displaystyle\cdot}$ $h(t)=x+tv$

{\begin{aligned}0&=\lim_{t\to 0}{\frac {f(x+tv)-f(x)-tDf(x)(v)}{t}}\\ &=\lim_{t\to 0}{\frac {f(x+tv)-f(x)}{t}}-Df(x)(v)=\nabla_{v}f(x) -Df(x)(v)\\\Pfeil nach rechts &\nabla f(\mathbf {x} )\cdot \mathbf {v} =Df(x)(v)=\nabla _{\mathbf {v} }{ f}(\mathbf{x})\end{ausgerichtet}}

Intuitiv repräsentiert die Richtungsableitung von f an einem Punkt x die Änderungsrate von f in Richtung von v bezüglich der Zeit, wenn man sich an x vorbeibewegt .

Nur die Richtung des Vektors verwenden

Der Winkel α zwischen der Tangente A und der Horizontalen ist maximal, wenn die Schnittebene die Richtung der Steigung A enthält .

In einem euklidischen Raum definieren einige Autoren die Richtungsableitung in Bezug auf einen beliebigen von Null verschiedenen Vektor v nach der Normierung , also unabhängig von seiner Größe und nur von seiner Richtung abhängig.

Diese Definition gibt die Zunahmerate von f pro Entfernungseinheit an, die in die durch v gegebene Richtung bewegt wird . In diesem Fall hat man

\nabla _{\mathbf {v} }{f}(\mathbf {x} )=\lim _{h\to 0}{\frac {f(\mathbf {x} +h\mathbf {v } )-f(\mathbf{x})}{h|\mathbf{v} |}},

oder falls f bei x differenzierbar ist ,

\nabla _{\mathbf {v} }{f}(\mathbf {x} )=\nabla f(\mathbf {x} )\cdot {\frac {\mathbf {v} }{|\mathbf {v} |}}.

Beschränkung auf einen Einheitsvektor

Im Kontext einer Funktion auf einem euklidischen Raum beschränken einige Texte den Vektor v auf einen Einheitsvektor . Mit dieser Einschränkung sind die beiden obigen Definitionen äquivalent.

Eigenschaften

Viele der bekannten Eigenschaften der gewöhnlichen Ableitung gelten für die gerichtete Ableitung. Dazu gehören für alle Funktionen f und g, die in einer Umgebung von p definiert sind und an p differenzierbar sind :

Summenregel :
$\nabla_{\mathbf{v}}(f+g)=\nabla_{\mathbf{v}}f+\nabla_{\mathbf{v}}g.$
Konstantenfaktorregel : Für jede Konstante c gilt
$\nabla_{\mathbf{v}}(cf)=c\nabla_{\mathbf{v}}f.$
Produktregel (oder Leibniz-Regel ):
$\nabla_{\mathbf {v}}(fg)=g\nabla_{\mathbf {v}}f+f\nabla_{\mathbf{v}}g.$
Kettenregel : Wenn g bei p differenzierbar istund h bei g ( p ), dann
$\nabla_{\mathbf {v}}(h\circ g)(\mathbf {p} )=h'(g(\mathbf{p}))\nabla_{\mathbf {v}}g (\mathbf{p}).$

In Differentialgeometrie

Sei $M$ eine differenzierbare Mannigfaltigkeit und $p$ ein Punkt von $M$ . Angenommen, $f$ eine Funktion in einer Nachbarschaft von definierten ist $p$ und differenzierbar bei $p$ . Wenn $v$ ein Tangentenvektor an $M$ bei $p ist$ , dann ist die Richtungsableitung von $f$ entlang $v$ , verschieden bezeichnet als $df (v)$ (siehe Äußere Ableitung ), (siehe Kovariante Ableitung ), (siehe Lie-Ableitung ) oder (siehe Tangentialraum § Definition über Ableitungen ), kann wie folgt definiert werden. Sei $γ$ $: [-1, 1] \to$ $M$ eine differenzierbare Kurve mit $γ$ $(0) =$ $p$ und $γ$ $'(0) =$ $v$ . Dann ist die Richtungsableitung definiert durch $\nabla_{\mathbf{v}}f(\mathbf{p})$ $L_{\mathbf{v}}f(\mathbf{p})$ ${\mathbf{v}}_{\mathbf{p}}(f)$

\nabla_{\mathbf {v}}f(\mathbf{p})=\left.{\frac {d}{d\tau}}f\circ \gamma (\tau)\right|_ {\tau =0}.

Diese Definition kann unabhängig von der Wahl von $γ$ bewiesen werden , vorausgesetzt, $γ$ wird in der vorgeschriebenen Weise so gewählt, dass $γ'(0) = v$ .

Das Lügen-Derivat

Die Lie-Ableitung eines Vektorfeldes entlang eines Vektorfeldes ergibt sich aus der Differenz zweier Richtungsableitungen (mit verschwindender Torsion): $W^{\mu}(x)$ $V^{\mu}(x)$

{\mathcal{L}}_{V}W^{\mu}=(V\cdot\nabla)W^{\mu}-(W\cdot\nabla)V^{\mu}.

Insbesondere für ein skalares Feld reduziert sich die Lie-Ableitung auf die Standardrichtungsableitung: ${\displaystyle\phi(x)}$

{\mathcal{L}}_{V}\phi =(V\cdot\nabla)\phi.

Der Riemann-Tensor

Richtungsableitungen werden oft in einführenden Ableitungen des Riemannschen Krümmungstensors verwendet . Betrachten Sie ein gekrümmtes Rechteck mit einem infinitesimalen Vektor δ entlang einer Kante und δ ′ entlang der anderen. Wir übersetzen einen Kovektor S entlang δ dann δ ′ und subtrahieren dann die Translation entlang δ ′ und dann δ . Anstatt die Richtungsableitung mit partiellen Ableitungen aufzubauen, verwenden wir die kovariante Ableitung . Der Übersetzungsoperator für δ ist also

1+\sum_{\nu}\delta ^{\nu}D_{\nu}=1+\delta\cdot D,

und für δ ′,

1+\sum_{\mu}\delta '^{\mu}D_{\mu}=1+\delta '\cdot D.

Der Unterschied zwischen den beiden Pfaden ist dann

(1+\delta '\cdot D)(1+\delta\cdot D)S^{\rho}-(1+\delta\cdot D)(1+\delta '\cdot D)S^ {\rho}=\sum_{\mu,\nu}\delta '^{\mu}\delta ^{\nu}[D_{\mu},D_{\nu}]S_{\rho}.

Man kann argumentieren, dass die Nichtkommutativität der kovarianten Ableitungen die Krümmung der Mannigfaltigkeit misst:

[D_{\mu},D_{\nu}]S_{\rho}=\pm\sum _{\sigma}R^{\sigma }{}_{\rho\mu\nu}S_{ \sigma},

wobei R der Riemannsche Krümmungstensor ist und das Vorzeichen von der Vorzeichenkonvention des Autors abhängt .

In der Gruppentheorie

Übersetzungen

In der Poincaré-Algebra können wir einen infinitesimalen Übersetzungsoperator P as . definieren

{\displaystyle\mathbf{P} =i\nabla.}

(das i sorgt dafür, dass P ein selbstadjungierter Operator ist ) Für eine endliche Verschiebung λ ist die unitäre Hilbertraum- Darstellung für Translationen

U({\boldsymbol {\lambda}})=\exp \left(-i{\boldsymbol {\lambda}}\cdot \mathbf{P} \right).

Indem wir die obige Definition des infinitesimalen Translationsoperators verwenden, sehen wir, dass der endliche Translationsoperator eine exponentielle Richtungsableitung ist:

U({\boldsymbol {\lambda}})=\exp \left({\boldsymbol {\lambda}}\cdot\nabla\right).

Dies ist ein Translationsoperator in dem Sinne, dass er auf multivariable Funktionen f ( x ) als . wirkt

U({\boldsymbol {\lambda}})f(\mathbf {x} )=\exp \left({\boldsymbol {\lambda}}\cdot \nabla \right)f(\mathbf {x} )=f(\mathbf{x}+{\boldsymbol{\lambda}}).

Beweis der letzten Gleichung —

In der Standardrechnung mit einer Variablen ist die Ableitung einer glatten Funktion f ( x ) definiert durch (für kleine ε )

{\frac {df}{dx}}={\frac {f(x+\varepsilon)-f(x)}{\varepsilon}}.

Dies kann umgeordnet werden, um f ( x + ε ) zu finden:

f(x+\varepsilon)=f(x)+\varepsilon\,{\frac {df}{dx}}=\left(1+\varepsilon\,{\frac {d}{dx}}\ rechts)f(x).

Daraus folgt, dass es sich um einen Übersetzungsoperator handelt. Dies wird sofort auf multivariable Funktionen f ( x ) verallgemeinert $[1+\varepsilon\,(d/dx)]$

f(\mathbf {x} +{\boldsymbol {\varepsilon}})=\left(1+{\boldsymbol {\varepsilon}}\cdot\nabla\right)f(\mathbf {x}).

Hier ist die Richtungsableitung entlang der infinitesimalen Verschiebung ε . Wir haben die infinitesimale Version des Übersetzungsoperators gefunden: ${\boldsymbol {\varepsilon}}\cdot\nabla$

U({\boldsymbol {\varepsilon}})=1+{\boldsymbol {\varepsilon}}\cdot\nabla.

Es ist offensichtlich, dass das Gruppenmultiplikationsgesetz U ( g ) U ( f ) = U ( gf ) die Form

U(\mathbf{a})U(\mathbf{b})=U(\mathbf{a+b}).

Nehmen wir also an, wir nehmen die endliche Verschiebung λ und teilen sie in N Teile ( N →∞ ist überall impliziert), so dass λ / N = ε . Mit anderen Worten,

{\boldsymbol {\lambda}}=N{\boldsymbol {\varepsilon}}.

Dann können wir durch N- maliges Anwenden von U ( ε ) U ( λ ) konstruieren :

[U({\boldsymbol {\varepsilon}})]^{N}=U(N{\boldsymbol {\varepsilon}})=U({\boldsymbol {\lambda}}).

Wir können nun unseren obigen Ausdruck für U( ε ) einsetzen:

[U({\boldsymbol {\varepsilon}})]^{N}=\left[1+{\boldsymbol {\varepsilon}}\cdot \nabla \right]^{N}=\left[1 +{\frac{{\boldsymbol {\lambda}}\cdot\nabla}{N}}\right]^{N}.

Verwenden der Identität

\exp(x)=\left[1+{\frac {x}{N}}\right]^{N},

wir haben

U({\boldsymbol {\lambda}})=\exp \left({\boldsymbol {\lambda}}\cdot\nabla\right).

Und da U ( ε ) f ( x )= f ( x + ε ) gilt

[U({\boldsymbol {\varepsilon}})]^{N}f(\mathbf{x})=f(\mathbf{x} +N{\boldsymbol {\varepsilon}})=f( \mathbf {x} +{\boldsymbol {\lambda}})=U({\boldsymbol {\lambda}})f(\mathbf {x} )=\exp \left({\boldsymbol {\lambda}}\ cdot \nabla \right)f(\mathbf{x}),

QED

Als technischer Hinweis ist dieses Verfahren nur möglich, weil die Übersetzungsgruppe eine abelsche Untergruppe ( Cartan-Subalgebra ) in der Poincaré-Algebra bildet. Insbesondere sollte das Gruppenmultiplikationsgesetz U ( a ) U ( b ) = U ( a + b ) nicht selbstverständlich sein. Wir stellen auch fest, dass Poincaré eine verbundene Lie-Gruppe ist. Es ist eine Gruppe von Transformationen T ( ξ ), die durch einen kontinuierlichen Satz reeller Parameter beschrieben werden . Das Gruppenmultiplikationsgesetz hat die Form $\xi^{a}$

T({\bar{\xi}})T(\xi)=T(f({\bar{\xi}},\xi)).

Als Koordinaten der Identität müssen wir haben $\xi^{a}=0$

f^{a}(\xi,0)=f^{a}(0,\xi)=\xi^{a}.

Die tatsächlichen Operatoren auf dem Hilbertraum werden durch unitäre Operatoren U ( T ( ξ )) dargestellt. In der obigen Notation haben wir das T unterdrückt ; wir schreiben nun U ( λ ) als U ( P ( λ )). Für eine kleine Nachbarschaft um die Identität ist die Potenzreihendarstellung

U(T(\xi))=1+i\sum_{a}\xi^{a}t_{a}+{\frac {1}{2}}\sum _{b,c} \xi^{b}\xi^{c}t_{bc}+\cdots

ist ziemlich gut. Angenommen, U(T(ξ)) bildet eine nichtprojektive Darstellung, dh

U(T({\bar{\xi}}))U(T(\xi))=U(T(f({\bar{\xi}},\xi))).

Die Erweiterung von f in die zweite Potenz ist

f^{a}({\bar{\xi}},\xi)=\xi^{a}+{\bar{\xi}}^{a}+\sum _{b,c} f^{abc}{\bar{\xi}}^{b}\xi^{c}.

Nach Erweiterung der Darstellungsmultiplikationsgleichung und Gleichsetzen der Koeffizienten haben wir die nichttriviale Bedingung

t_{bc}=-t_{b}t_{c}-i\sum _{a}f^{abc}t_{a}.

Da per Definition symmetrisch in seinen Indizes ist, haben wir den Standard- Lie-Algebra- Kommutator: $t_{ab}$

[t_{b},t_{c}]=i\sum_{a}(-f^{abc}+f^{acb})t_{a}=i\sum _{a}C^ {abc}t_{a},

mit C die Strukturkonstante . Die Generatoren für Übersetzungen sind partielle Ableitungsoperatoren, die kommutieren:

\left[{\frac {\partial }{\partial x^{b}}},{\frac {\partial }{\partial x^{c}}}\right]=0.

Dies impliziert, dass die Strukturkonstanten verschwinden und damit auch die quadratischen Koeffizienten in der f-Entwicklung. Das bedeutet, dass f einfach additiv ist:

f_{\text{abelian}}^{a}({\bar {\xi}},\xi)=\xi^{a}+{\bar {\xi}}^{a},

und damit für abelsche Gruppen,

U(T({\bar{\xi}}))U(T(\xi))=U(T({\bar{\xi}}+\xi)).

QED

Drehungen

Der Rotationsoperator enthält auch eine Richtungsableitung. Der Rotationsoperator für einen Winkel θ , dh um einen Betrag θ = | & thgr; | um eine Achse parallel zu is ${\hat{\theta}}={\boldsymbol {\theta}}/\theta$

U(R(\mathbf {\theta}))=\exp(-i\mathbf {\theta} \cdot\mathbf{L}).

Hier ist L der Vektoroperator, der SO(3) erzeugt :

\mathbf {L} ={\begin{pmatrix}0&0&0\\0&0&1\\0&-1&0\end{pmatrix}}\mathbf {i} +{\begin{pmatrix}0&0&-1\\0&0&0\\ 1&0&0\end{pmatrix}}\mathbf {j} +{\begin{pmatrix}0&1&0\\-1&0&0\\0&0&0\end{pmatrix}}\mathbf {k} .

Geometrisch lässt sich zeigen, dass eine infinitesimale Rechtsdrehung den Ortsvektor x um . ändert

\mathbf {x} \rightarrow \mathbf {x} -\delta {\boldsymbol {\theta}}\times \mathbf {x} .

Unter infinitesimaler Drehung würden wir also erwarten:

U(R(\delta {\boldsymbol {\theta}}))f(\mathbf {x} )=f(\mathbf {x} -\delta {\boldsymbol {\theta}}\times \mathbf {x} )=f(\mathbf {x} )-(\delta {\boldsymbol {\theta}}\times \mathbf{x})\cdot\nabla f.

Es folgt dem

U(R(\delta\mathbf{\theta}))=1-(\delta\mathbf{\theta}\times\mathbf{x})\cdot\nabla.

Nach dem gleichen Exponentiationsverfahren wie oben erhalten wir den Rotationsoperator in der Positionsbasis, der eine exponentielle Richtungsableitung ist:

U(R(\mathbf {\theta}))=\exp(-(\mathbf {\theta} \times \mathbf{x})\cdot\nabla).

Normale Ableitung

Eine Normalenableitung ist eine Richtungsableitung, die in der Richtung normal (d. h. orthogonal ) zu einer Fläche im Raum oder allgemeiner entlang eines Normalenvektorfelds orthogonal zu einer Hyperfläche genommen wird . Siehe zum Beispiel Neumann-Randbedingung . Wenn die Normalenrichtung mit bezeichnet wird , dann wird die Normalenableitung einer Funktion f manchmal als bezeichnet . In anderen Notationen, ${\displaystyle\mathbf{n}}$ ${\frac {\partial f}{\partial\mathbf {n} }}$

{\frac {\partialf}{\partial\mathbf{n}}}=\nabla f(\mathbf{x})\cdot\mathbf{n} =\nabla_{\mathbf{n}} {f}(\mathbf {x} )={\frac {\partial f}{\partial\mathbf {x}}}\cdot \mathbf {n} =Df(\mathbf {x} )[\mathbf {n } ].

In der Kontinuumsmechanik von Festkörpern

Mehrere wichtige Ergebnisse der Kontinuumsmechanik erfordern die Ableitungen von Vektoren in Bezug auf Vektoren und von Tensoren in Bezug auf Vektoren und Tensoren. Die Richtungsrichtlinie bietet einen systematischen Weg, diese Derivate zu finden.

Die Definitionen von Richtungsderivaten für verschiedene Situationen sind unten angegeben. Es wird angenommen, dass die Funktionen ausreichend glatt sind, sodass Ableitungen gebildet werden können.

Ableitungen von skalarwertigen Funktionen von Vektoren

Sei f ( v ) eine reellwertige Funktion des Vektors v. Dann ist die Ableitung von f (v) nach v (oder bei v) der Vektor, der durch sein Skalarprodukt definiert ist, wobei jeder Vektor u ist

{\frac {\partial f}{\partial\mathbf {v}}}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\ frac {\rm {d}}{{\rm {d}}\alpha}}~f(\mathbf{v} +\alpha~\mathbf{u})\right]_{\alpha=0}

für alle Vektoren u. Das obige Skalarprodukt ergibt einen Skalar, und wenn u ein Einheitsvektor ist, ergibt sich die Richtungsableitung von f bei v in u-Richtung.

Eigenschaften:

Wenn dann $f(\mathbf{v})=f_{1}(\mathbf{v})+f_{2}(\mathbf{v})$ ${\frac {\partial f}{\partial\mathbf {v}}}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial\mathbf {v } }}+{\frac{\partial f_{2}}{\partial\mathbf{v}}}\right)\cdot\mathbf{u}$
Wenn dann $f(\mathbf{v})=f_{1}(\mathbf{v})~f_{2}(\mathbf{v})$ ${\frac {\partial f}{\partial\mathbf {v}}}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial\mathbf {v } }}\cdot \mathbf {u} \right)~f_{2}(\mathbf {v} )+f_{1}(\mathbf {v} )~\left({\frac {\partial f_{2 }}{\partial\mathbf{v}}}\cdot\mathbf{u}\right)$
Wenn dann $f(\mathbf{v})=f_{1}(f_{2}(\mathbf{v}))$ ${\frac {\partial f}{\partial\mathbf {v}}}\cdot \mathbf {u} ={\frac {\partial f_{1}}{\partial f_{2}}}~ {\frac{\partialf_{2}}{\partial\mathbf{v}}}\cdot\mathbf{u}$

Ableitungen von vektorwertigen Funktionen von Vektoren

Sei f(v) eine vektorwertige Funktion des Vektors v. Dann ist die Ableitung von f(v) nach v (oder bei v) der durch sein Skalarprodukt definierte Tensor zweiter Ordnung, wobei jeder Vektor u . ist

{\frac {\partial\mathbf {f} }{\partial\mathbf {v}}}\cdot\mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf { u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha}}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}

für alle Vektoren u. Das obige Skalarprodukt ergibt einen Vektor, und wenn u ein Einheitsvektor ist, ergibt sich die Richtungsableitung von f bei v in der Richtung u.

Eigenschaften:

Wenn dann ${\displaystyle\mathbf{f} (\mathbf{v})=\mathbf{f}_{1}(\mathbf{v})+\mathbf{f}_{2}(\mathbf{v})}$ ${\frac {\partial\mathbf {f} }{\partial\mathbf {v}}}\cdot \mathbf {u} =\left({\frac {\partial\mathbf {f} _{1 }}{\partial\mathbf{v}}}+{\frac{\partial\mathbf{f}_{2}}{\partial\mathbf{v}}}\right)\cdot\mathbf{u}$
Wenn dann $\mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v})\times \mathbf {f} _{2}(\mathbf {v})$ ${\frac {\partial\mathbf {f} }{\partial\mathbf {v}}}\cdot \mathbf {u} =\left({\frac {\partial\mathbf {f} _{1 }}{\partial\mathbf{v}}}\cdot\mathbf{u}\right)\times\mathbf{f}_{2}(\mathbf{v})+\mathbf{f}_{1} (\mathbf{v})\times \left({\frac{\partial\mathbf{f}_{2}}{\partial\mathbf{v}}}\cdot\mathbf{u}\right)$
Wenn dann $\mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {f} _{2}(\mathbf {v}))$ ${\frac {\partial\mathbf {f}} }{\partial\mathbf {v}}}\cdot \mathbf {u} ={\frac {\partial\mathbf {f} _{1}}{ \partial\mathbf{f}_{2}}}\cdot\left({\frac {\partial\mathbf{f}_{2}}{\partial\mathbf{v}}}\cdot\mathbf{u } \rechts)$

Ableitungen skalarwertiger Funktionen von Tensoren zweiter Ordnung

Sei eine reellwertige Funktion des Tensors zweiter Ordnung . Dann ist die Ableitung von nach (oder bei ) in Richtung der Tensor zweiter Ordnung definiert als $f({\boldsymbol {S}})$ ${\boldsymbol {S}}$ $f({\boldsymbol {S}})$ ${\boldsymbol {S}}$ ${\boldsymbol {S}}$ ${\boldsymbol {T}}$

{\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha}}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\ rechts]_{\alpha =0}

für alle Tensoren zweiter Ordnung . ${\boldsymbol {T}}$

Eigenschaften:

Wenn dann $f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})+f_{2}({\boldsymbol {S}})$ ${\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial { \boldsymbol {S}}}}+{\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}\right):{\boldsymbol {T}}$
Wenn dann $f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})~f_{2}({\boldsymbol {S}})$ ${\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial { \boldsymbol {S}}}}:{\boldsymbol {T}}\right)~f_{2}({\boldsymbol {S}})+f_{1}({\boldsymbol {S}})~\left ({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)$
Wenn dann $f({\boldsymbol {S}})=f_{1}(f_{2}({\boldsymbol {S}}))$ ${\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial f_{2} }}~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}}:{\boldsymbol {T}}\right)$

Ableitungen tensorwertiger Funktionen von Tensoren zweiter Ordnung

Sei eine tensorwertige Funktion zweiter Ordnung des Tensors zweiter Ordnung . Dann ist die Ableitung von nach (oder bei ) in Richtung der Tensor vierter Ordnung definiert als ${\boldsymbol {F}}({\boldsymbol {S}})$ ${\boldsymbol {S}}$ ${\boldsymbol {F}}({\boldsymbol {S}})$ ${\boldsymbol {S}}$ ${\boldsymbol {S}}$ ${\boldsymbol {T}}$

{\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {F}}({ \boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}

für alle Tensoren zweiter Ordnung . ${\boldsymbol {T}}$

Eigenschaften:

Wenn dann ${\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})+{\boldsymbol {F}}_{ 2}({\boldsymbol{S}})$ ${\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}} }}\right):{\boldsymbol {T}}$
Wenn dann ${\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_ {2}({\boldsymbol {S}})$ ${\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}({\boldsymbol { S}})+{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\ partiell {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)$
Wenn dann ${\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S} }))$ ${\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial {\boldsymbol {F} }_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)$
Wenn dann $f({\boldsymbol {S}})=f_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))$ ${\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial {\boldsymbol { F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T} }\rechts)$

Siehe auch

Anmerkungen

Verweise

Hildebrand, FB (1976). Erweitertes Kalkül für Anwendungen . Lehrlingssaal. ISBN 0-13-011189-9.
KF Riley; Abgeordneter Hobson; SJ Bence (2010). Mathematische Methoden für Physik und Ingenieurwissenschaften . Cambridge University Press. ISBN 978-0-521-86153-3.
Shapiro, A. (1990). „Über Konzepte der Richtungsdifferenzierbarkeit“. Zeitschrift für Optimierungstheorie und Anwendungen . 66 (3): 477–487. doi : 10.1007/BF00940933 .

Externe Links

Medien im Zusammenhang mit direktionaler Ableitung bei Wikimedia Commons

Richtungsderivate bei MathWorld .
Richtungsableitung bei PlanetMath .

Languages

In other projects

Richtungsableitung - Directional derivative

Inhalt

Definition

Für differenzierbare Funktionen

Nur die Richtung des Vektors verwenden

Beschränkung auf einen Einheitsvektor

Eigenschaften

In Differentialgeometrie

Das Lügen-Derivat

Der Riemann-Tensor

In der Gruppentheorie

Übersetzungen

Drehungen

Normale Ableitung

In der Kontinuumsmechanik von Festkörpern

Ableitungen von skalarwertigen Funktionen von Vektoren

Ableitungen von vektorwertigen Funktionen von Vektoren

Ableitungen skalarwertiger Funktionen von Tensoren zweiter Ordnung

Ableitungen tensorwertiger Funktionen von Tensoren zweiter Ordnung

Siehe auch

Anmerkungen

Verweise

Externe Links